Integral substitusi
|
Read other articles:

Greek mythological character For the moth, see Hemeroplanes triptolemus. Buzyges and Dysaules redirect here. For the insect genera, see Buzyges (butterfly) and Dysaules (mantis). TriptolemusPatron of the Eleusinian MysteriesFounder of AgricultureJudge of the AfterlifeDetail of Triptolemus standing between Demeter and Persephone, relief from the National Archaeological Museum of Athens.AbodeEleusis, Elysium, HadesMountDragon-drawn chariotParentsOceanus and Gaia, or Celeus and Metanira Greek de...
サッカーオーストリア女子代表国または地域 オーストリア協会 オーストリアサッカー協会(ÖFB)監督 イレーネ・フアマン最多出場選手 サーラ・プンティガム(118試合)最多得点選手 ニーナ・ブルガー(53得点) ホームカラー アウェイカラー 初の国際試合 1990年8月25日 オーストリア 1 - 5 スイス(スイス、リヒターズヴィル)最大差勝利試合 2003年5月10日、13日&...

Mary Kempton Trotter (Pennsylvania, 3 augustus 1859 - Parijs, 10 april 1925) was een Amerikaanse impressionistisch kunstenares, deels opgeleid in de Verenigde Staten en deels in Parijs. Ze schilderde met olieverf, voornamelijk portretten, landschappen en natuurtaferelen. Schilderij van Mary K. Trotter: Kinderen met panfluit Geboorte en jeugd Mary was de dochter van William Trotter, een groothandelaar in kruidenierswaren en Anna Patterson. Ze had een jongere broer Albert (1860-1932). Studies Z...
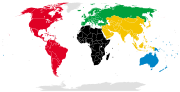
Komite Olimpiade Nasional (atau NOC) adalah konstituen nasional dari gerakan Olimpiade seluruh dunia. Bergantung pada Komite Olimpiade Internasional, mereka bertanggungjawab atas pengaturan partisipasi atlet dalam Olimpiade. Mereka dapat mencalonkan kota di negara mereka sebagai kandidat untuk Olimpiade selanjutnya. NOC juga mempromosikan pengembangan atlet dan pelatihan pelatih dan ofisial pada tingkat nasional di dalam negara mereka. Pada 2008, terdapat 205 NOC, mewakili negara berdaulat da...

Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Maio de 2019) Este é um artigo sobreHistória da Letónia Antecedentes • Éstios • Povos fínicos - livônios • Povos bálticos - curônios, semigálios e latigálios • Cruzadas do Norte (1193-1316) Parte do Confederação da Livônia • Irmãos Livô...

The Right ReverendSidney Catlin PartridgeBishop of West MissouriChurchEpiscopal ChurchDioceseWest MissouriElected1911In office1911-1930PredecessorEdward Robert AtwillSuccessorRobert Nelson SpencerOrdersOrdination1885by William Jones BooneConsecrationFebruary 2, 1900by John McKimPersonal detailsBorn(1857-09-01)September 1, 1857New York City, New York, U.S.DiedJune 22, 1930(1930-06-22) (aged 72)Kansas City, Missouri, U.S.BuriedForest Hill Calvary CemeteryKansas City, Missouri, U....

غوفستاون الإحداثيات 43°01′13″N 71°36′01″W / 43.020277777778°N 71.600277777778°W / 43.020277777778; -71.600277777778 تاريخ التأسيس 1761 تقسيم إداري البلد الولايات المتحدة[1][2] التقسيم الأعلى هيلسبوروغ خصائص جغرافية المساحة 37.5 ميل مربع ارتفاع 94 متر عدد السكا

提示:此条目的主题不是南洋大学、南洋理工學院或南京大學。 南洋理工大學Nanyang Technological University校训自強不息、力求上進[1][2][3][4]创办时间1955年 南洋大学 1981年 南洋理工学院1991年 南洋理工大学学校类型國立大學捐贈基金S$17.17億 [5]校监新加坡總統(現任:尚達曼)校长何德华教授副校长林杉教授 常务副校长兼教务长沈祖堯教授

Comic book series Futurama ComicsThe front cover of issue #1StoryMultiple (based on characters created by Matt Groening)InkMultipleDateNovember 22, 2000 - July 18, 2018Pages25First publicationNovember 22, 2000 Futurama Comics is a comic book series based on the television show Futurama published by Bongo Comics. It has been published bi-monthly in the United States since November 2000 (apart from a brief break for the crossover). It has been published in the United Kingdom (with an altered or...
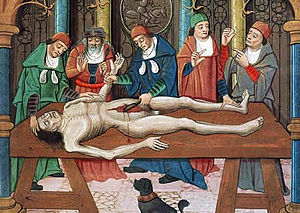
Aspect of history Dissection of a cadaver, 15th-century painting The history of anatomy extends from the earliest examinations of sacrificial victims to the sophisticated analyses of the body performed by modern anatomists and scientists. Written descriptions of human organs and parts can be traced back thousands of years to ancient Egyptian papyri, where attention to the body was necessitated by their highly elaborate burial practices. Theoretical considerations of the structure and function...

Brahmin sub-caste of India Saraswat Brahmins are Hindu Brahmins, who are spread over widely separated regions spanning from Kashmir in North India to Konkan in West India to Kanara (coastal region of Karnataka) and Kerala in South India. The word Saraswat is derived from the Rigvedic Sarasvati River.[1][2][3] Classification Saraswats Brahmins are classified under the Pancha Gauda Brahmin classification of the Brahmin community in India. In Western and South India, alon...

2003 single by Beyoncé featuring Sean Paul Baby BoySingle by Beyoncé featuring Sean Paulfrom the album Dangerously in Love and Dutty Rock B-sideSummertime (remix)ReleasedAugust 3, 2003 (2003-08-03)RecordedFebruary 2003[1]Studio The Hit Factory (New York City, New York) South Beach (Miami, Florida)[2] Genre Dancehall R&B Length4:04Label Columbia Music World Songwriter(s) Beyoncé Knowles Scott Storch Sean Paul Henriques Robert Waller Shawn Carter Producer(s...

This article is about the South Korean TV show. For other uses, see 9 (disambiguation). South Korean TV series or program NinePromotional posterAlso known as9 Nine: Time Traveling Nine TimesGenreRomance Time travel MysteryWritten bySong Jae-jung Kim Yoon-jooDirected byKim Byung-sooStarringLee Jin-wookJo Yoon-heeComposerNam Hye-seungCountry of originSouth KoreaOriginal languageKoreanNo. of episodes20ProductionExecutive producersKim Young-gyuLee Jin-suk [ko]Choi Young-gunProdu...

Former nighttime theme park event This article is about the nighttime event at Disney California Adventure. For the spinning tea cup ride, see Mad Tea Party. Mad T Party BandDisney California AdventureAreaHollywood LandStatusRemovedOpening dateMay 26, 2012 (2012-05-26) (Original) May 20, 2015 (2015-05-20)Closing dateDecember 1, 2014 (2014-12-01) (Original) March 31, 2016ReplacedElecTRONicaReplaced byDisney California Adventure Food & Wine Festi...

1969 studio album by Isaac HayesHot Buttered SoulStudio album by Isaac HayesReleasedJune 1969[1][2]RecordedMarch - May 1969Studio Ardent Studios, Memphis, Tennessee Tera Shirma Studios, Detroit, Michigan Genre Progressive soul[3] psychedelic soul[4] Length45:24LabelEnterpriseProducerAl Bell, Marvell Thomas, Allen JonesIsaac Hayes chronology Presenting Isaac Hayes(1968) Hot Buttered Soul(1969) The Isaac Hayes Movement(1970) Singles from Hot Buttered Soul...

Style of architecture, art, and design in the United Kingdom in the mid-1880s Poster by Frances MacDonald (1896) The Modern Style is a style of architecture, art, and design that first emerged in the United Kingdom in the mid-1880s. It was the first Art Nouveau style worldwide, and it represents the evolution of the Arts and Crafts movement which was native to Great Britain. The Modern Style provided the base and intellectual background for the Art Nouveau movement and was adapted by other co...

1966 studio album by The Horace Silver Quintet Plus J.J. JohnsonThe Cape Verdean BluesStudio album by The Horace Silver Quintet Plus J.J. JohnsonReleasedEarly January 1966[1]RecordedOctober 1 & 22, 1965StudioVan Gelder Studio, Englewood Cliffs, NJGenreJazzLength43:43LabelBlue NoteBST 84220ProducerAlfred LionHorace Silver chronology Song for My Father(1964) The Cape Verdean Blues(1966) The Jody Grind(1966) Professional ratingsReview scoresSourceRatingThe Penguin Guide to Ja...

Suburban Community in Halifax, Nova Scotia, CanadaSpryfieldSuburban CommunitySpryfieldCoordinates: 44°36′42″N 63°37′04″W / 44.61167°N 63.61778°W / 44.61167; -63.61778CountryCanadaProvinceNova ScotiaMunicipalityHalifaxCommunitySpryfieldMunicipal DistrictDistrict 11 (Spryfield-Sambro Loop-Prospect Road)Founded1769Amalgamated with Halifax1 April 1996Area[1] • Land10.74 km2 (4.15 sq mi)Population (2016)[2] �...

Binary star system in the constellation Taurus UX Tauri An artist's conception of a circumstellar disk around UX Tauri A, along with several hypothetical protoplanets. Observation dataEpoch J2000.0 Equinox J2000.0 Constellation Taurus Right ascension 04h 30m 03.99626s[1] Declination +18° 13′ 49.4355″[1] Apparent magnitude (V) +10.80[2] Characteristics Spectral type K2Ve + M1Ve[3] Astro...

LGV Perpignan - Figueras Carte de la ligne Le viaduc de la Muga, à Pont de Molins. Pays France, Espagne Historique Mise en service 2009 – 2012 Concessionnaires TP Ferro (2004 – 2016)Línea Figueras Perpignan S.A. (depuis 2016) Caractéristiques techniques Numéro officiel 837 000 Longueur 44,4 km Vitesse maximale commerciale 300 km/h Vitesse maximale de conception 350 km/h Écartement standard (1,435 m) Électrification 25 kV – 50&...





![{\displaystyle {\frac {d}{dx}}\left[{\frac {1}{48}}(2x^{3}+1)^{8}\right]={\frac {1}{6}}(2x^{3}+1)^{7}(6x^{2})=(2x^{3}+1)^{7}(x^{2}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9592fba9ffbc6b9298e87a0db652fdc83c34a3d0)














