积 (范畴论)

范畴论中，积（或直积）的概念提取了集合的笛卡儿积、群的积、环的积、拓扑空间的积等概念的共性。本质上讲，一组对象的积是到这些对象都有态射的对象中最具代表性的。

定义

给定范畴C。C中一对象集{X_i | i ∈ I}的积为满足下面泛性质的偶(X, (π_i))，其中X为一对象，π_i : X → X_i（i ∈ I）为一组态射：对任意对象Y及其到X_i的一组态射f_i，存在唯一的态射f : Y → X满足，对任意i ∈ I，f_i = π_i f。即，对任意i，下图可交换。

Universal product of the product

若该组对象仅有两个，积通常用X₁×X₂来表示。上图变为：

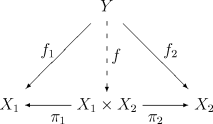Universal product of the product

此时，此唯一态射f也常表示为<f₁,f₂>。

讨论

积为范畴论中的一种极限。积也即C中离散子范畴的极限。积不一定存在。但若存在，则由其定义易知其在同构的意義下唯一。

空积（I为空时所得的积）即终对象。

若C中对任意基于I的对象集均存在积，则该积也可以看做一个从C^I到C的函子。

集合{X_i}的积通常记为∏_i X_i。态射π_i也称为自然投影。如下自然同构成立：

${\displaystyle \operatorname {Hom} _{C}\left(Y,\prod _{i\in I}X_{i}\right)\simeq \prod _{i\in I}\operatorname {Hom} _{C}(Y,X_{i})}$

（Hom_C(U,V)表示C中从U到V的态射集；左侧的积为范畴意义上的积、右侧的为集合的笛卡儿积）。

若I为有限集，例如I = {1,...,n}，则X₁,...,X_n的积通常记为X₁×...×X_n。

设C存在有限积，采用上述积函子的定义，并用1表示C的终对象（空积），则下列自然同构成立：

${\displaystyle X\times (Y\times Z)\simeq (X\times Y)\times Z\simeq X\times Y\times Z}$

${\displaystyle X\times 1\simeq 1\times X\simeq X}$

${\displaystyle X\times Y\simeq Y\times X}$

上述为构成一个交换幺半群的条件。

举例

• Set的积为集合的笛卡儿积。
• 由偏序构成的范畴：一组元素的积为该组元素的最大下界。

参见

• 泛性质
• 上积 – 积的对偶概念
• 极限与上极限
• Equalizer
• 反极限
• 笛卡儿闭范畴