|
õ╣łÕŹŖń»äń¢ć
Õ╝ĄķćÅń»äń¢ć’╝łtensor category’╝ē’╝īµł¢µø░Õ╣║ÕŹŖń»äń¢ć’╝łmonoidal category’╝ē’╝ī ńø┤Ķ”║Õ£░Ķ¼ø’╝īµś»ÕĆŗķģŹõĖŖÕ╝ĄķćÅń®ŹńÜäķś┐Ķ▓ØńłŠń»äń¢ć’╝łabelian category’╝ē’╝īÕÅ»ńĢČõĮ£ńÆ░ńÜäń»äń¢ćÕī¢ŃĆé
Õ«ÜńŠ®
µĢĖÕŁĖõĖŁ’╝īõĖĆÕĆŗÕ╝ĄķćÅń»äń¢ć’╝łtensor category’╝īµł¢ń©▒Õ╣║ÕŹŖń»äń¢ć monoidal category’╝ēµś»õĖĆÕĆŗÕīģÕɽբ«õĖĆÕĆŗÕ░ŹĶ▒ĪńÜäķøÖń»äń¢ć’╝ēbicategory’╝ēŃĆé
µø┤ÕģĘķ½öńÜäµÅÅĶ┐░’╝ÜõĖĆÕĆŗÕ╝ĄķćÅń»äń¢ćµś»
- õĖĆÕĆŗń»äń¢ć
 ; ;
- Ķó½Ķ│”õ║łÕ╝ĄķćÅń®Ź’╝īÕŹ│õĖĆÕĆŗõ║īÕģāÕćĮÕŁÉ
 ; ;
- Ķó½Ķ│”õ║łõĖĆÕĆŗÕ¢«õĮŹÕ░ŹĶ▒Ī
 ; ;
- Ķó½Ķ│”õ║łõĖēńĄäĶć¬ńäČÕÉīµ¦ŗµśĀÕ░ä’╝Ü
- ńĄÉÕÉłÕŁÉ
 : :  ; ;
- ÕĘ”/ÕÅ│Õ¢«õĮŹÕŁÉ: Ķć¬ńäČÕÉīµ¦ŗµśĀÕ░ä
 , ,  : :
 , , ; ;
- µ╗┐ĶČ│õ╗źõĖŗńøĖÕ«╣µóØõ╗Č:
- 每
 , ,  , ,  , ,    , ,
![]() - ÕÆī
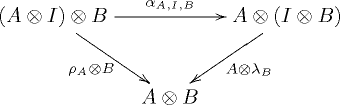 - ķāĮõ║żµÅø.///
Õ£©ķĆÖõ╗źõĖŖÕģ®ķüōńøĖÕ«╣µóØõ╗ČõĖŗ’╝īõ╗╗õĮĢõ╗źńĄÉÕÉłÕŁÉ,ÕĘ”ÕÅ│Õ¢«õĮŹÕŁÉÕÆīÕ╝ĄķćÅń®ŹńĄäµłÉńÜäÕ£¢ĶĪ©ķāĮõ║żµÅø’╝īÕøĀńé║
Mac Lane ÕćØĶüÜÕ«ÜńÉå(Mac Lane's coherence theorem):
µ»ÅÕĆŗÕ╣║ÕŹŖń»äń¢ćķāĮ Õ╣║ÕŹŖńŁēÕā╣(monoidally equivalent) µ¢╝õĖĆÕÜ┤µĀ╝Õ╣║ÕŹŖń»äń¢ć’╝łĶ”ŗõĖŗ’╝ē.
ÕÜ┤µĀ╝Õ╣║ÕŹŖń»äń¢ć
ÕÜ┤µĀ╝Õ╣║ÕŹŖń»äń¢ć(strict monoidal category)
µś»ÕĆŗÕ╣║ÕŹŖń»äń¢ć ’╝īÕģČĶć¬ńäȵģŗÕ░ä  , ,  ÕÆī ÕÆī  ķāĮµś»µüåńŁēÕĮ▒Õ░ä. ķāĮµś»µüåńŁēÕĮ▒Õ░ä.
ÕÅ¢õ╗╗õĖĆ ń»äń¢ć  , µłæõ╗¼ÕÅ»µ¦ŗń»ēÕģČ Ķć¬ńö▒ÕÜ┤µĀ╝Õ╣║ÕŹŖń»äń¢ć , µłæõ╗¼ÕÅ»µ¦ŗń»ēÕģČ Ķć¬ńö▒ÕÜ┤µĀ╝Õ╣║ÕŹŖń»äń¢ć
 : :
- Õ░ŹĶ▒Ī’╝ÜÕģȵ»ÅõĖĆÕ░ŹĶ▒Īµś»õĖĆõĖ▓ńö▒
 ĶŻĪķØóńÜäÕ░ŹĶ▒ĪńĄäµłÉõ╣ŗµ£ēķÖÉÕ║ÅÕłŚ ĶŻĪķØóńÜäÕ░ŹĶ▒ĪńĄäµłÉõ╣ŗµ£ēķÖÉÕ║ÅÕłŚ  )’╝ø )’╝ø
- µģŗÕ░ä’╝ÜńĢČõĖöÕāģńĢČ
 µÖé’╝īµłæõ╗¼Õ£©õ║īÕĆŗÕ░ŹĶ▒Ī µÖé’╝īµłæõ╗¼Õ£©õ║īÕĆŗÕ░ŹĶ▒Ī  ÕÆī ÕÆī  õ╣ŗķ¢ōÕ«ÜńŠ® µģŗÕ░ä:µ»Å õ╣ŗķ¢ōÕ«ÜńŠ® µģŗÕ░ä:µ»Å  -µģŗÕ░ä µś»õĖĆõĖ▓ńö▒ -µģŗÕ░ä µś»õĖĆõĖ▓ńö▒  -µģŗÕ░äńĄäµłÉńÜäµ£ēķÖÉÕ║ÅÕłŚ -µģŗÕ░äńĄäµłÉńÜäµ£ēķÖÉÕ║ÅÕłŚ  ’╝ø ’╝ø
- Õ╝ĄķćÅń®Ź’╝Ü õ║īÕĆŗ
 -Õ░ŹĶ▒Ī -Õ░ŹĶ▒Ī ÕÅŖ ÕÅŖ  õ╣ŗÕ╝ĄķćÅń®Ź’╝ī µłæõ╗¼Õ«ÜńŠ®ńé║ µŁżõ║īµ£ēķÖÉÕ║ÅÕłŚõ╣ŗõĖ▓µÄź(concatenation) õ╣ŗÕ╝ĄķćÅń®Ź’╝ī µłæõ╗¼Õ«ÜńŠ®ńé║ µŁżõ║īµ£ēķÖÉÕ║ÅÕłŚõ╣ŗõĖ▓µÄź(concatenation)  ’╝ø ÕÉīµ©ŻÕ£░õ╗╗õĮĢõ║ī ’╝ø ÕÉīµ©ŻÕ£░õ╗╗õĮĢõ║ī  -µģŗÕ░äõ╣ŗÕ╝ĄķćÅń®Ź’╝ī µłæõ╗¼Õ«ÜńŠ®ńé║ÕģČõĖ▓µÄźŃĆé -µģŗÕ░äõ╣ŗÕ╝ĄķćÅń®Ź’╝ī µłæõ╗¼Õ«ÜńŠ®ńé║ÕģČõĖ▓µÄźŃĆé
µīē’╝ܵŁżń«Śń¼”  ’╝īÕÉæńö▒õ╗╗õĖĆ ń»äń¢ć ’╝īÕÉæńö▒õ╗╗õĖĆ ń»äń¢ć  ķģŹõĖŖ ķģŹõĖŖ  ’╝īÕÅ»µÄ©Õ╗ŻÕł░ ’╝īÕÅ»µÄ©Õ╗ŻÕł░  õĖŖńÜäÕÜ┤µĀ╝-2-Õ¢«ÕŁÉ ’╝łstrict 2-monad’╝ēŃĆé õĖŖńÜäÕÜ┤µĀ╝-2-Õ¢«ÕŁÉ ’╝łstrict 2-monad’╝ēŃĆé
õŠŗ
ÕÅ¢õ╗╗õĖĆń»äń¢ć’╝īĶŗźõ╗źÕģČÕ╣│ÕĖĖń»äń¢ćń®ŹõĮ£Õ╝ĄķćÅń®Ź’╝īõ╗źÕģČńĄéÕ░ŹĶ▒ĪõĮ£Õ¢«õĮŹÕ░ŹĶ▒Ī’╝īÕē浳Éńé║õĖĆÕĆŗÕ╝ĄķćÅń»äń¢ćŃĆé
õ║”ÕÅ»ÕÅ¢õ╗╗õĖĆń»äń¢ć’╝īõ╗źÕģČķżśń®Ź’╝łco-product’╝ēõĮ£Õ╝ĄķćÅń®Ź’╝īõ╗źÕģČÕ¦ŗÕ░ŹĶ▒ĪõĮ£Õ¢«õĮŹÕ░ŹĶ▒Ī’╝īõ║”µłÉõĖĆÕĆŗÕ╝ĄķćÅń»äń¢ćŃĆé
’╝łµŁżõ║īõŠŗÕ»”ńé║Õ░Źń©▒õ╣łÕŹŖń»äń¢ćńĄÉµ¦ŗŃĆé’╝ē
õĮåõ║”µ£ēĶ©▒ÕżÜÕ╝ĄķćÅń»äń¢ć’╝łõŠŗÕ”é’╝Ü -Mod’╝īÕ”éõĖŗ’╝ē’╝īÕģČÕ╝ĄķćÅń®Ź µŚóķØ× ń»äń¢ćń®Ź õ║”ķØ× ń»äń¢ćķżśń®ŹŃĆé -Mod’╝īÕ”éõĖŗ’╝ē’╝īÕģČÕ╝ĄķćÅń®Ź µŚóķØ× ń»äń¢ćń®Ź õ║”ķØ× ń»äń¢ćķżśń®ŹŃĆé
õ╗źõĖŗĶłēÕ╝ĄķćÅń»äń¢ćõ║īõŠŗŌĆöŌĆöÕÉæķćÅń®║ķ¢ōń»äń¢ćÕÆīķøåÕÉłń»äń¢ćŌĆöŌĆöõĖ”ĶĪ©µśÄÕģČķĪ×µ»ö’╝Ü
ńøĖķŚ£ńÜäńĄÉµ¦ŗ
- ÕŠłÕżÜÕ╝ĄķćÅń»äń¢ćµø┤ķĆ▓õĖƵŁźµ£ē ĶŠ«, õ║żµÅøµģŗÕ░ä or Õ░üķ¢ēńŁēń╗ōµ¦ŗ. Ķ®│Ķ”ŗõĖŗĶ┐░ÕÅāĶĆāŃĆé
- õ╣łÕŹŖÕćĮÕŁÉńé║õ║īÕ╝ĄķćÅń»äń¢ć’╝łõ╣łÕŹŖń»äń¢ć’╝ēķ¢ōŃĆüõ┐ØÕŁśÕ╝ĄķćÅń®ŹńĄÉµ¦ŗõ╣ŗÕćĮÕŁÉ’╝ø õ╣łÕŹŖµģŗÕ░äńé║õ║īõ╣łÕŹŖÕćĮÕŁÉķ¢ōõ╣ŗµģŗÕ░ä’╝łĶć¬ńäČĶ«ŖµÅø (natural transformations)’╝ēŃĆé
- õĖĆĶł¼õ╣łÕŹŖńŠżõ╣ŗµ”éÕ┐ĄÕÅ»µÄ©Õ╗ŻµłÉõ╣łÕŹŖń»äń¢ćõĖŁńÜäõ╣łÕŹŖÕ░ŹĶ▒ĪŃĆéÕ░żÕģČĶĆģ’╝īÕÅ»Ķ”¢õĖĆÕÜ┤µĀ╝õ╣łÕŹŖń»äń¢ćõĮ£ ń»äń¢ćõ╣ŗŃĆīń»äń¢ćŃĆŹ CatõĖŁńÜäõ╣łÕŹŖÕ░ŹĶ▒Ī’╝łõĖ”õ╗źÕŹĪµ░Åń®Źńé║õ╣łÕŹŖńĄÉµ¦ŗ’╝ēŃĆé
- õĖŖµ£ēńĢīõ║żÕŹŖµĀ╝ µ¦ŗµłÉõĖĆÕÜ┤µĀ╝Õ░Źń©▒õ╣łÕŹŖń»äń¢ć’╝ÜÕģČń®Źńé║õ║ż’╝īĶĆīÕ¢«õĮŹÕģāÕēćńé║ķĀéŃĆé
µćēńö©
ÕÅāĶĆā
- Mac Lane, Saunders (1963). "Natural Associativity and Commutativity". Rice University Studies 49, 28ŌĆō46.
- Kelly, G. Max (1964). "On MacLane's Conditions for Coherence of Natural Associativities, Commutativities, etc." Journal of Algebra 1, 397ŌĆō402
- Joyal, André; Street, Ross (1993). "Braided Tensor Categories". Advances in Mathematics 102, 20ŌĆō78.
- Mac Lane, Saunders (1997), Categories for the Working Mathematician (2nd ed.). New York: Springer-Verlag.
- Baez, John, Definitions ’╝łķĪĄķØóÕŁśµĪŻÕżćõ╗Į’╝īÕŁśõ║Äõ║ÆĶüöńĮæµĪŻµĪłķ”å’╝ē
- : <<Braided Category>>, <<Encyclopaedia of Mathematics>>,Springer On-line Reference Works ’╝łķĪĄķØóÕŁśµĪŻÕżćõ╗Į’╝īÕŁśõ║Äõ║ÆĶüöńĮæµĪŻµĪłķ”å’╝ē
|
|