數學 上,克利福德代数 (Clifford algebra )是由具有二次型 的向量空間 生成的單位 結合代數 。作為域上的代數 ,其推廣實數系 、複數系 、四元數系 等超複數系 ,以及外代数 。[ 1] [ 2] 威廉·金顿·克利福德 。
研究克里福代数的理論有時也稱為克里福代數,其與二次型論和正交群理論 緊密聯繫。其在几何 、理論物理 、數碼圖像處理 中有很多应用。其主要贡献者有:威廉·哈密顿 (四元数),赫尔曼·格拉斯曼 (外代数),威廉·金顿·克利福德 ,David Hestenes
最常見的克里福代數是正交克里福代數 ,又稱(偽 )黎曼克里福代數 。另一類是扭對稱克里福代數 。[ 3]
設有域
K
{\displaystyle K}
向量空間
V
{\displaystyle V}
二次型
Q
:
V
→ → -->
K
{\displaystyle Q:V\to K}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
V
{\displaystyle V}
最自由 單位 結合代數 ,但須滿足[ a]
v
2
=
Q
(
v
)
1
∀ ∀ -->
v
∈ ∈ -->
V
,
{\displaystyle v^{2}=Q(v)1\quad \forall v\in V,}
其中左邊的平方是該代數中的乘法,而右邊的
1
{\displaystyle 1}
乘法單位元 。所謂「最自由」,可以用泛性質 嚴格定義,詳見下節 。
若
V
{\displaystyle V}
Q
{\displaystyle Q}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
C
l
p
,
q
(
R
)
{\displaystyle \mathrm {Cl} _{p,q}(\mathbb {R} )}
V
{\displaystyle V}
p
{\displaystyle p}
e
i
{\displaystyle e_{i}}
e
i
2
=
+
1
{\displaystyle e_{i}^{2}=+1}
q
{\displaystyle q}
e
i
2
=
− − -->
1
{\displaystyle e_{i}^{2}=-1}
R
{\displaystyle \mathbb {R} }
正交對角化
由
V
{\displaystyle V}
張量代數
⨁ ⨁ -->
n
≥ ≥ -->
0
V
⊗ ⊗ -->
V
⊗ ⊗ -->
⋯ ⋯ -->
⊗ ⊗ -->
V
⏟ ⏟ -->
n
{\displaystyle \bigoplus _{n\geq 0}\underbrace {V\otimes V\otimes \cdots \otimes V} _{n}}
V
{\displaystyle V}
n
{\displaystyle n}
張量積 ,對所有
n
{\displaystyle n}
直和 。故相應的克里福代數會是該張量代數對元素
v
⊗ ⊗ -->
v
− − -->
Q
(
v
)
1
{\displaystyle v\otimes v-Q(v)1}
v
{\displaystyle v}
V
{\displaystyle V}
雙邊理想 的商 。張量積導出在商代數的乘積以串接 表示(例如
u
v
{\displaystyle uv}
克里福代數有指明的子空間
V
{\displaystyle V}
嵌入 的像 。若只得與克里福代數同構 的
K
{\displaystyle K}
若底域
K
{\displaystyle K}
特徵 不為
2
{\displaystyle 2}
v
2
=
Q
(
v
)
1
∀ ∀ -->
v
∈ ∈ -->
V
{\displaystyle v^{2}=Q(v)1\ \forall v\in V}
u
v
+
v
u
=
2
⟨ ⟨ -->
u
,
v
⟩ ⟩ -->
1
∀ ∀ -->
u
,
v
∈ ∈ -->
V
,
{\displaystyle uv+vu=2\langle u,v\rangle 1\quad \forall u,v\in V,}
其中
⟨ ⟨ -->
u
,
v
⟩ ⟩ -->
=
1
2
(
Q
(
u
+
v
)
− − -->
Q
(
u
)
− − -->
Q
(
v
)
)
{\displaystyle \langle u,v\rangle ={\frac {1}{2}}\left(Q(u+v)-Q(u)-Q(v)\right)}
定義的對稱雙線性形式 與二次型
Q
{\displaystyle Q}
極化恆等式 。
特徵為
2
{\displaystyle 2}
c
h
a
r
(
K
)
=
2
{\displaystyle \mathrm {char} (K)=2}
Q
{\displaystyle Q}
Q
(
v
)
=
⟨ ⟨ -->
v
,
v
⟩ ⟩ -->
{\displaystyle Q(v)=\langle v,v\rangle }
⟨ ⟨ -->
∙ ∙ -->
,
∙ ∙ -->
⟩ ⟩ -->
{\displaystyle \langle \bullet ,\bullet \rangle }
Q
{\displaystyle Q}
正交基 。本條目不少命題的條件皆要求特徵不為
2
{\displaystyle 2}
2
{\displaystyle 2}
克里福代數與外代數 密切相關。外代數是克里福代數的特例:若在克里福代數的定義中,取
Q
=
0
{\displaystyle Q=0}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
Q
{\displaystyle Q}
K
{\displaystyle K}
2
{\displaystyle 2}
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
線性同構 。換言之,兩者作為向量空間自然地同構 ,但其上的乘法有分別。特徵為
2
{\displaystyle 2}
外代數 更豐富的結構,因為用到
Q
{\displaystyle Q}
克里福代數為濾套代數 相伴的分次代數
具體而言,克里福代數可視為外代數的「量子化」(見量子群 ),正如外爾代數 對稱代數
外爾代數和克里福代數還具有*-代數 超代數 典範對易與反對易關係代數
設
V
{\displaystyle V}
域
K
{\displaystyle K}
向量空間 ,
Q
:
V
→ → -->
K
{\displaystyle Q:V\to K}
V
{\displaystyle V}
二次型 。多數情況下,域
K
{\displaystyle K}
實域
R
{\displaystyle \mathbb {R} }
複域
C
{\displaystyle \mathbb {C} }
有限域
F
q
{\displaystyle \mathbb {F} _{q}}
克里福代數
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
(
A
0
,
i
)
{\displaystyle (A_{0},i)}
[ b] [ 5]
A
0
{\displaystyle A_{0}}
K
{\displaystyle K}
單位 結合代數 ,而線性映射
i
:
V
→ → -->
C
l
(
V
,
Q
)
{\displaystyle i:V\to \mathrm {Cl} (V,Q)}
v
∈ ∈ -->
V
{\displaystyle v\in V}
i
(
v
)
2
=
Q
(
v
)
1
{\displaystyle i(v)^{2}=Q(v)1}
(
A
0
,
i
)
{\displaystyle (A_{0},i)}
泛性質 :給定
K
{\displaystyle K}
A
{\displaystyle A}
j
:
V
→ → -->
A
{\displaystyle j:V\to A}
j
(
v
)
2
=
Q
(
v
)
1
A
∀ ∀ -->
v
∈ ∈ -->
V
{\displaystyle j(v)^{2}=Q(v)1_{A}\quad \forall v\in V}
(其中
1
A
{\displaystyle 1_{A}}
A
{\displaystyle A}
代數同態
f
:
C
l
(
V
,
Q
)
→ → -->
A
{\displaystyle f:\mathrm {Cl} (V,Q)\to A}
可交換 (即
f
∘ ∘ -->
i
=
j
{\displaystyle f\circ i=j}
二次型
Q
{\displaystyle Q}
⟨ ⟨ -->
v
,
v
⟩ ⟩ -->
=
Q
(
v
)
{\displaystyle \langle v,v\rangle =Q(v)}
雙線性形式
⟨ ⟨ -->
∙ ∙ -->
,
∙ ∙ -->
⟩ ⟩ -->
{\displaystyle \langle \bullet ,\bullet \rangle }
j
{\displaystyle j}
j
(
v
)
j
(
v
)
=
⟨ ⟨ -->
v
,
v
⟩ ⟩ -->
1
A
∀ ∀ -->
v
∈ ∈ -->
V
.
{\displaystyle j(v)j(v)=\langle v,v\rangle 1_{A}\quad \forall v\in V.}
當基域的特徵非
2
{\displaystyle 2}
j
(
v
)
j
(
w
)
+
j
(
w
)
j
(
v
)
=
(
⟨ ⟨ -->
v
,
w
⟩ ⟩ -->
+
⟨ ⟨ -->
w
,
v
⟩ ⟩ -->
)
1
A
∀ ∀ -->
v
,
w
∈ ∈ -->
V
,
{\displaystyle j(v)j(w)+j(w)j(v)=(\langle v,w\rangle +\langle w,v\rangle )1_{A}\quad \forall v,w\in V,}
其中雙線性型不妨限定為對稱雙線性型。
以上描述的克里福代數必定存在,能藉以下一般方法構造:先選取由
V
{\displaystyle V}
張量代數
T
(
V
)
{\displaystyle T(V)}
商 ,保證基本恆等式成立。對於克里福代數,所需
T
(
V
)
{\displaystyle T(V)}
理想
I
Q
{\displaystyle I_{Q}}
v
⊗ ⊗ -->
v
− − -->
Q
(
v
)
1
{\displaystyle v\otimes v-Q(v)1}
的元素生成,其中
v
{\displaystyle v}
V
{\displaystyle V}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
T
(
V
)
/
I
Q
{\displaystyle T(V)/I_{Q}}
商承繼的環 乘積有時稱為克里福積 [ 6] :8–9 ,以免與外代數的外積
∧ ∧ -->
{\displaystyle \wedge }
⋅ ⋅ -->
{\displaystyle \,\cdot \,}
有上述
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
V
{\displaystyle V}
C
l
{\displaystyle \mathrm {Cl} }
i
{\displaystyle i}
單射 ,故通常隱藏
i
{\displaystyle i}
V
{\displaystyle V}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
線性子空間 。
因為克里福代數可由泛性質定義,所以
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
函子性 ,即
C
l
{\displaystyle \mathrm {Cl} }
函子 ,其定義域為具有二次型的
K
{\displaystyle K}
範疇 (其態射 為保二次型的線性映射),陪域為結合
K
{\displaystyle K}
由於
V
{\displaystyle V}
Q
{\displaystyle Q}
2
{\displaystyle 2}
V
{\displaystyle V}
正交基 ,即其元素
e
i
{\displaystyle e_{i}}
⟨ ⟨ -->
e
i
,
e
j
⟩ ⟩ -->
=
0
(
i
≠ ≠ -->
j
)
{\displaystyle \langle e_{i},e_{j}\rangle =0\quad (i\neq j)}
⟨ ⟨ -->
e
i
,
e
i
⟩ ⟩ -->
=
Q
(
e
i
)
{\displaystyle \langle e_{i},e_{i}\rangle =Q(e_{i})}
基本克里福恆等式推出,對於正交基,有
e
i
e
j
=
− − -->
e
j
e
i
(
i
≠ ≠ -->
j
)
{\displaystyle e_{i}e_{j}=-e_{j}e_{i}\quad (i\neq j)}
e
i
2
=
Q
(
e
i
)
{\displaystyle e_{i}^{2}=Q(e_{i})}
此關係使正交基元間的運算很容易。給定
V
{\displaystyle V}
e
i
1
e
i
2
⋯ ⋯ -->
e
i
k
{\displaystyle e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}}
置換的奇偶性 在前面加上正負號。
若
V
{\displaystyle V}
K
{\displaystyle K}
維數 為
n
{\displaystyle n}
{
e
1
,
e
2
,
… … -->
,
e
n
}
{\displaystyle \{e_{1},e_{2},\ldots ,e_{n}\}}
(
V
,
Q
)
{\displaystyle (V,Q)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
K
{\displaystyle K}
{
e
i
1
e
i
2
⋯ ⋯ -->
e
i
k
∣ ∣ -->
1
≤ ≤ -->
i
1
<
i
2
<
⋯ ⋯ -->
<
i
k
≤ ≤ -->
n
,
0
≤ ≤ -->
k
≤ ≤ -->
n
}
{\displaystyle \{e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}\mid 1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n,\ 0\leq k\leq n\}}
在上式中,空乘積(
k
=
0
{\displaystyle k=0}
單位元 。由於每個
e
i
{\displaystyle e_{i}}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
dim
-->
Cl
-->
(
V
,
Q
)
=
2
n
.
{\displaystyle \dim \operatorname {Cl} (V,Q)=2^{n}.}
克里福代數的重要例子源自實 或複 向量空間及其上非退化的二次型給出。
本節的例子
C
l
p
,
q
(
R
)
{\displaystyle \mathrm {Cl} _{p,q}(\mathbb {R} )}
C
l
n
(
C
)
{\displaystyle \mathrm {Cl} _{n}(\mathbb {C} )}
A
{\displaystyle A}
A
⊕ ⊕ -->
A
{\displaystyle A\oplus A}
A
{\displaystyle A}
R
{\displaystyle \mathbb {R} }
C
{\displaystyle \mathbb {C} }
H
{\displaystyle \mathbb {H} }
全個矩陣環 。此類代數的完整分類,見克里福代數的分類
克里福代數有時稱為幾何代數
有限維實向量空間上的非退化二次型必等價於某個標準對角型:
Q
(
v
)
=
v
1
2
+
⋯ ⋯ -->
+
v
p
2
− − -->
v
p
+
1
2
− − -->
⋯ ⋯ -->
− − -->
v
p
+
q
2
,
{\displaystyle Q(v)=v_{1}^{2}+\dots +v_{p}^{2}-v_{p+1}^{2}-\dots -v_{p+q}^{2},}
其中
n
=
p
+
q
{\displaystyle n=p+q}
(
p
,
q
)
{\displaystyle (p,q)}
符號
R
p
,
q
{\displaystyle \mathbb {R} ^{p,q}}
R
p
,
q
{\displaystyle \mathbb {R} ^{p,q}}
C
l
p
,
q
(
R
)
{\displaystyle \mathrm {Cl} _{p,q}(\mathbb {R} )}
C
l
n
(
R
)
{\displaystyle \mathrm {Cl} _{n}(\mathbb {R} )}
C
l
n
,
0
(
R
)
{\displaystyle \mathrm {Cl} _{n,0}(\mathbb {R} )}
C
l
0
,
n
(
R
)
{\displaystyle \mathrm {Cl} _{0,n}(\mathbb {R} )}
R
p
,
q
{\displaystyle \mathbb {R} ^{p,q}}
基
{
e
1
,
e
2
,
… … -->
,
e
n
}
{\displaystyle \{e_{1},e_{2},\ldots ,e_{n}\}}
n
=
p
+
q
{\displaystyle n=p+q}
p
{\displaystyle p}
+
1
{\displaystyle +1}
q
{\displaystyle q}
− − -->
1
{\displaystyle -1}
C
l
p
,
q
(
R
)
{\displaystyle \mathrm {Cl} _{p,q}(\mathbb {R} )}
p
{\displaystyle p}
+
1
{\displaystyle +1}
q
{\displaystyle q}
− − -->
1
{\displaystyle -1}
低維的例子有:
C
l
0
,
0
(
R
)
{\displaystyle \mathrm {Cl} _{0,0}(\mathbb {R} )}
R
{\displaystyle \mathbb {R} }
C
l
0
,
1
(
R
)
{\displaystyle \mathrm {Cl} _{0,1}(\mathbb {R} )}
e
1
{\displaystyle e_{1}}
− − -->
1
{\displaystyle -1}
複數域
C
{\displaystyle \mathbb {C} }
C
l
0
,
2
(
R
)
{\displaystyle \mathrm {Cl} _{0,2}(\mathbb {R} )}
{
1
,
e
1
,
e
2
,
e
1
e
2
}
{\displaystyle \{1,e_{1},e_{2},e_{1}e_{2}\}}
− − -->
1
{\displaystyle -1}
四元數系
H
{\displaystyle \mathbb {H} }
C
l
0
,
3
(
R
)
{\displaystyle \mathrm {Cl} _{0,3}(\mathbb {R} )}
直和
H
⊕ ⊕ -->
H
{\displaystyle \mathbb {H} \oplus \mathbb {H} }
分裂複四元數系
也可以研究複域上的克里福代數。
n
{\displaystyle n}
Q
(
z
)
=
z
1
2
+
z
2
2
+
⋯ ⋯ -->
+
z
n
2
.
{\displaystyle Q(z)=z_{1}^{2}+z_{2}^{2}+\dots +z_{n}^{2}.}
由此,對每個維數
n
{\displaystyle n}
n
{\displaystyle n}
C
l
n
(
C
)
{\displaystyle \mathrm {Cl} _{n}(\mathbb {C} )}
最小的幾個例子為:
C
l
0
(
C
)
≅ ≅ -->
C
{\displaystyle \mathrm {Cl} _{0}(\mathbb {C} )\cong \mathbb {C} }
複數系 ,
C
l
1
(
C
)
≅ ≅ -->
C
⊕ ⊕ -->
C
{\displaystyle \mathrm {Cl} _{1}(\mathbb {C} )\cong \mathbb {C} \oplus \mathbb {C} }
雙複數系 ,
C
l
2
(
C
)
≅ ≅ -->
M
2
(
C
)
{\displaystyle \mathrm {Cl} _{2}(\mathbb {C} )\cong M_{2}(\mathbb {C} )}
複四元數系 ,其中
M
n
(
C
)
{\displaystyle M_{n}(\mathbb {C} )}
n
× × -->
n
{\displaystyle n\times n}
本節將會構造哈密頓 的四元數系 ,作為克里福代數
C
l
0
,
3
(
R
)
{\displaystyle \mathrm {Cl} _{0,3}(\mathbb {R} )}
設
V
{\displaystyle V}
R
3
{\displaystyle \mathbb {R} ^{3}}
Q
{\displaystyle Q}
v
,
w
∈ ∈ -->
R
3
{\displaystyle v,w\in \mathbb {R} ^{3}}
v
⋅ ⋅ -->
w
=
v
1
w
1
+
v
2
w
2
+
v
3
w
3
{\displaystyle v\cdot w=v_{1}w_{1}+v_{2}w_{2}+v_{3}w_{3}}
給出。
現引入向量
v
,
w
{\displaystyle v,w}
v
w
{\displaystyle vw}
v
w
+
w
v
=
− − -->
2
(
v
⋅ ⋅ -->
w
)
.
{\displaystyle vw+wv=-2(v\cdot w).}
(此處有負號,以使該代數與四元數的聯繫更清晰。)
設
e
1
,
e
2
,
e
3
{\displaystyle e_{1},e_{2},e_{3}}
R
3
{\displaystyle \mathbb {R} ^{3}}
e
2
e
3
=
− − -->
e
3
e
2
,
e
3
e
1
=
− − -->
e
1
e
3
,
e
1
e
2
=
− − -->
e
2
e
1
,
{\displaystyle e_{2}e_{3}=-e_{3}e_{2},\,\,\,e_{3}e_{1}=-e_{1}e_{3},\,\,\,e_{1}e_{2}=-e_{2}e_{1},}
且
e
1
2
=
e
2
2
=
e
3
2
=
− − -->
1.
{\displaystyle e_{1}^{2}=e_{2}^{2}=e_{3}^{2}=-1.}
克里福代數
C
l
0
,
3
(
R
)
{\displaystyle \mathrm {Cl} _{0,3}(\mathbb {R} )}
A
=
a
0
+
a
1
e
1
+
a
2
e
2
+
a
3
e
3
+
a
4
e
2
e
3
+
a
5
e
3
e
1
+
a
6
e
1
e
2
+
a
7
e
1
e
2
e
3
.
{\displaystyle A=a_{0}+a_{1}e_{1}+a_{2}e_{2}+a_{3}e_{3}+a_{4}e_{2}e_{3}+a_{5}e_{3}e_{1}+a_{6}e_{1}e_{2}+a_{7}e_{1}e_{2}e_{3}.}
若只考慮偶次項,則得到偶子代數
C
l
0
,
3
[
0
]
(
R
)
{\displaystyle \mathrm {Cl} _{0,3}^{[0]}(\mathbb {R} )}
q
=
q
0
+
q
1
e
2
e
3
+
q
2
e
3
e
1
+
q
3
e
1
e
2
.
{\displaystyle q=q_{0}+q_{1}e_{2}e_{3}+q_{2}e_{3}e_{1}+q_{3}e_{1}e_{2}.}
若定義四元數的基元
i
,
j
,
k
{\displaystyle i,j,k}
i
=
e
2
e
3
,
j
=
e
3
e
1
,
k
=
e
1
e
2
,
{\displaystyle i=e_{2}e_{3},j=e_{3}e_{1},k=e_{1}e_{2},}
則可知
C
l
0
,
3
[
0
]
(
R
)
{\displaystyle \mathrm {Cl} _{0,3}^{[0]}(\mathbb {R} )}
四元數 代數同構,理由是:
i
2
=
(
e
2
e
3
)
2
=
e
2
e
3
e
2
e
3
=
− − -->
e
2
e
2
e
3
e
3
=
− − -->
1
,
{\displaystyle i^{2}=(e_{2}e_{3})^{2}=e_{2}e_{3}e_{2}e_{3}=-e_{2}e_{2}e_{3}e_{3}=-1,}
i
j
=
e
2
e
3
e
3
e
1
=
− − -->
e
2
e
1
=
e
1
e
2
=
k
,
{\displaystyle ij=e_{2}e_{3}e_{3}e_{1}=-e_{2}e_{1}=e_{1}e_{2}=k,}
且
i
j
k
=
e
2
e
3
e
3
e
1
e
1
e
2
=
− − -->
1
,
{\displaystyle ijk=e_{2}e_{3}e_{3}e_{1}e_{1}e_{2}=-1,}
與四元數的運算法則一致。
本節構造二元四元數系 [ 7] [ 8]
設向量空間
V
{\displaystyle V}
R
4
{\displaystyle \mathbb {R} ^{4}}
Q
{\displaystyle Q}
R
3
{\displaystyle \mathbb {R} ^{3}}
d
{\displaystyle d}
v
,
w
∈ ∈ -->
R
4
{\displaystyle v,w\in \mathbb {R} ^{4}}
d
(
v
,
w
)
=
v
1
w
1
+
v
2
w
2
+
v
3
w
3
.
{\displaystyle d(v,w)=v_{1}w_{1}+v_{2}w_{2}+v_{3}w_{3}.}
換言之,此退化純量積只考慮將
R
4
{\displaystyle \mathbb {R} ^{4}}
R
3
{\displaystyle \mathbb {R} ^{3}}
向量
v
,
w
{\displaystyle v,w}
v
w
{\displaystyle vw}
v
w
+
w
v
=
− − -->
2
d
(
v
,
w
)
.
{\displaystyle vw+wv=-2\,d(v,w).}
同上節,負號是為了明確該代數與四元數系的對應關係。
記
R
4
{\displaystyle \mathbb {R} ^{4}}
e
1
,
e
2
,
e
3
,
e
4
{\displaystyle e_{1},e_{2},e_{3},e_{4}}
e
m
e
n
=
− − -->
e
n
e
m
(
m
≠ ≠ -->
n
)
,
{\displaystyle e_{m}e_{n}=-e_{n}e_{m}\,\,\,(m\neq n),}
及
e
1
2
=
e
2
2
=
e
3
2
=
− − -->
1
,
e
4
2
=
0.
{\displaystyle e_{1}^{2}=e_{2}^{2}=e_{3}^{2}=-1,\,\,e_{4}^{2}=0.}
克里福代數
C
l
(
R
4
,
d
)
{\displaystyle \mathrm {Cl} (\mathbb {R} ^{4},d)}
C
l
0
,
3
,
1
(
R
)
{\displaystyle \mathrm {Cl} _{0,3,1}(\mathbb {R} )}
+
1
,
− − -->
1
,
0
{\displaystyle +1,-1,0}
C
l
[
0
]
(
R
4
,
d
)
{\displaystyle \mathrm {Cl} ^{[0]}(\mathbb {R} ^{4},d)}
H
=
h
0
+
h
1
e
2
e
3
+
h
2
e
3
e
1
+
h
3
e
1
e
2
+
h
4
e
4
e
1
+
h
5
e
4
e
2
+
h
6
e
4
e
3
+
h
7
e
1
e
2
e
3
e
4
.
{\displaystyle H=h_{0}+h_{1}e_{2}e_{3}+h_{2}e_{3}e_{1}+h_{3}e_{1}e_{2}+h_{4}e_{4}e_{1}+h_{5}e_{4}e_{2}+h_{6}e_{4}e_{3}+h_{7}e_{1}e_{2}e_{3}e_{4}.}
於是,可分別定義四元數基元
i
,
j
,
k
{\displaystyle i,j,k}
二元數 基元
ε ε -->
{\displaystyle \varepsilon }
i
=
e
2
e
3
,
j
=
e
3
e
1
,
k
=
e
1
e
2
,
ε ε -->
=
e
1
e
2
e
3
e
4
,
{\displaystyle i=e_{2}e_{3},j=e_{3}e_{1},k=e_{1}e_{2},\,\,\varepsilon =e_{1}e_{2}e_{3}e_{4},}
從而給出
C
l
(
R
4
,
d
)
{\displaystyle \mathrm {Cl} (\mathbb {R} ^{4},d)}
二元四元數
要驗證二元四元數的乘法法則,可以計算
ε ε -->
2
=
(
e
1
e
2
e
3
e
4
)
2
=
e
1
e
2
e
3
e
4
e
1
e
2
e
3
e
4
=
− − -->
e
1
e
2
e
3
(
e
4
e
4
)
e
1
e
2
e
3
=
0
,
{\displaystyle \varepsilon ^{2}=(e_{1}e_{2}e_{3}e_{4})^{2}=e_{1}e_{2}e_{3}e_{4}e_{1}e_{2}e_{3}e_{4}=-e_{1}e_{2}e_{3}(e_{4}e_{4})e_{1}e_{2}e_{3}=0,}
和
ε ε -->
i
=
(
e
1
e
2
e
3
e
4
)
e
2
e
3
=
e
1
e
2
e
3
e
4
e
2
e
3
=
e
2
e
3
(
e
1
e
2
e
3
e
4
)
=
i
ε ε -->
.
{\displaystyle \varepsilon i=(e_{1}e_{2}e_{3}e_{4})e_{2}e_{3}=e_{1}e_{2}e_{3}e_{4}e_{2}e_{3}=e_{2}e_{3}(e_{1}e_{2}e_{3}e_{4})=i\varepsilon .}
後者的計算中,
e
1
{\displaystyle e_{1}}
e
4
{\displaystyle e_{4}}
ε ε -->
{\displaystyle \varepsilon }
i
,
j
,
k
{\displaystyle i,j,k}
設
K
{\displaystyle K}
2
{\displaystyle 2}
對於
dim
-->
V
=
1
{\displaystyle \dim V=1}
Q
{\displaystyle Q}
d
i
a
g
(
a
)
{\displaystyle \mathrm {diag} (a)}
v
∈ ∈ -->
V
{\displaystyle v\in V}
Q
(
v
)
=
a
{\displaystyle Q(v)=a}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
K
[
x
]
/
(
x
2
− − -->
a
)
{\displaystyle K[x]/(x^{2}-a)}
x
2
=
a
{\displaystyle x^{2}=a}
x
{\displaystyle x}
K
{\displaystyle K}
更具體而言,有三種情況:
若
a
=
0
{\displaystyle a=0}
Q
{\displaystyle Q}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
K
{\displaystyle K}
二元數代數 。
若
a
{\displaystyle a}
K
{\displaystyle K}
C
l
(
V
,
Q
)
≅ ≅ -->
K
⊕ ⊕ -->
K
{\displaystyle \mathrm {Cl} (V,Q)\cong K\oplus K}
其餘情況下,
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
K
{\displaystyle K}
域擴張
K
(
a
)
{\displaystyle K({\sqrt {a}})}
對於
dim
-->
V
=
2
{\displaystyle \dim V=2}
Q
{\displaystyle Q}
d
i
a
g
(
a
,
b
)
{\displaystyle \mathrm {diag} (a,b)}
a
,
b
{\displaystyle a,b}
Q
{\displaystyle Q}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
x
,
y
{\displaystyle x,y}
K
{\displaystyle K}
x
,
y
{\displaystyle x,y}
x
2
=
a
,
y
2
=
b
,
x
y
=
− − -->
y
x
{\displaystyle x^{2}=a,\ y^{2}=b,\ xy=-yx}
於是
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
四元數代數
(
a
,
b
)
K
{\displaystyle (a,b)_{K}}
a
=
b
=
− − -->
1
{\displaystyle a=b=-1}
K
=
R
{\displaystyle K=\mathbb {R} }
H
=
(
− − -->
1
,
− − -->
1
)
R
{\displaystyle \mathbb {H} =(-1,-1)_{\mathbb {R} }}
作為特殊情況,若有某個
x
∈ ∈ -->
V
{\displaystyle x\in V}
Q
(
x
)
=
1
{\displaystyle Q(x)=1}
C
l
(
V
,
Q
)
≅ ≅ -->
M
2
(
K
)
{\displaystyle \mathrm {Cl} (V,Q)\cong M_{2}(K)}
給定向量空間
V
{\displaystyle V}
外代數
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
V
{\displaystyle V}
K
{\displaystyle K}
2
{\displaystyle 2}
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
自然同構 (而在特徵
2
{\displaystyle 2}
Q
=
0
{\displaystyle Q=0}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
V
{\displaystyle V}
Q
{\displaystyle Q}
#作為外代數的量子化 。)原有的外積仍有不取決於
Q
{\displaystyle Q}
描述以上同構的簡單方法是:先取
V
{\displaystyle V}
{
e
1
,
e
2
,
… … -->
,
e
n
}
{\displaystyle \{e_{1},e_{2},\ldots ,e_{n}\}}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
#基與維數 所述)。定義映射
f
:
C
l
(
V
,
Q
)
→ → -->
∧ ∧ -->
(
V
)
{\displaystyle f:\mathrm {Cl} (V,Q)\to \wedge (V)}
e
i
1
e
i
2
⋯ ⋯ -->
e
i
k
↦ ↦ -->
e
i
1
∧ ∧ -->
e
i
2
∧ ∧ -->
⋯ ⋯ -->
∧ ∧ -->
e
i
k
,
{\displaystyle e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}\mapsto e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}},}
並線性擴展。注意此處用到
{
e
1
,
e
2
,
… … -->
,
e
n
}
{\displaystyle \{e_{1},e_{2},\ldots ,e_{n}\}}
f
{\displaystyle f}
若
K
{\displaystyle K}
特徵 為
0
{\displaystyle 0}
f
k
:
V
× × -->
⋯ ⋯ -->
× × -->
V
⏟ ⏟ -->
k
→ → -->
C
l
(
V
,
Q
)
{\displaystyle f_{k}:\underbrace {V\times \cdots \times V} _{k}\to \mathrm {Cl} (V,Q)}
f
k
(
v
1
,
… … -->
,
v
k
)
=
1
k
!
∑ ∑ -->
σ σ -->
∈ ∈ -->
S
k
s
g
n
(
σ σ -->
)
v
σ σ -->
(
1
)
⋯ ⋯ -->
v
σ σ -->
(
k
)
,
{\displaystyle f_{k}(v_{1},\ldots ,v_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}{\rm {sgn}}(\sigma )\,v_{\sigma (1)}\cdots v_{\sigma (k)},}
其求和符號中,
σ σ -->
{\displaystyle \sigma }
k
{\displaystyle k}
對稱群
S
k
{\displaystyle S_{k}}
f
k
{\displaystyle f_{k}}
反對稱 ,其導出獨一個映射
f
k
′
:
∧ ∧ -->
k
(
V
)
→ → -->
C
l
(
V
,
Q
)
{\displaystyle f_{k}':\wedge ^{k}(V)\to \mathrm {Cl} (V,Q)}
直和
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
也可以從更高等的觀點,在
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
濾過 張量代數
T
(
V
)
{\displaystyle T(V)}
F
0
⊂ ⊂ -->
F
1
⊂ ⊂ -->
F
2
⊂ ⊂ -->
⋯ ⋯ -->
{\displaystyle F^{0}\subset F^{1}\subset F^{2}\subset \cdots }
F
k
{\displaystyle F^{k}}
階 不高於
k
{\displaystyle k}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
相伴的分次代數
Gr
F
-->
Cl
-->
(
V
,
Q
)
=
⨁ ⨁ -->
k
F
k
/
F
k
− − -->
1
{\displaystyle \operatorname {Gr} _{F}\operatorname {Cl} (V,Q)=\bigoplus _{k}F^{k}/F^{k-1}}
與外代數
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
F
k
{\displaystyle F^{k}}
F
k
+
1
{\displaystyle F^{k+1}}
2
{\displaystyle 2}
本節假設特徵非
2
{\displaystyle 2}
[ c]
克里福代數為
Z
/
2
{\displaystyle \mathbb {Z} /2}
分次代數 超代數
V
{\displaystyle V}
v
↦ ↦ -->
− − -->
v
{\displaystyle v\mapsto -v}
關於原點對稱 )保持二次型
Q
{\displaystyle Q}
自同構
α α -->
:
Cl
-->
(
V
,
Q
)
→ → -->
Cl
-->
(
V
,
Q
)
.
{\displaystyle \alpha :\operatorname {Cl} (V,Q)\to \operatorname {Cl} (V,Q).}
由於
α α -->
{\displaystyle \alpha }
對合 (即其平方為恆同映射 ),可以將
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
α α -->
{\displaystyle \alpha }
Cl
-->
(
V
,
Q
)
=
Cl
[
0
]
-->
(
V
,
Q
)
⊕ ⊕ -->
Cl
[
1
]
-->
(
V
,
Q
)
,
{\displaystyle \operatorname {Cl} (V,Q)=\operatorname {Cl} ^{[0]}(V,Q)\oplus \operatorname {Cl} ^{[1]}(V,Q),}
其中
Cl
[
i
]
-->
(
V
,
Q
)
=
{
x
∈ ∈ -->
Cl
-->
(
V
,
Q
)
∣ ∣ -->
α α -->
(
x
)
=
(
− − -->
1
)
i
x
}
.
{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)=\left\{x\in \operatorname {Cl} (V,Q)\mid \alpha (x)=(-1)^{i}x\right\}.}
由於
α α -->
{\displaystyle \alpha }
Cl
[
i
]
-->
(
V
,
Q
)
Cl
[
j
]
-->
(
V
,
Q
)
=
Cl
[
i
+
j
]
-->
(
V
,
Q
)
,
{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)\operatorname {Cl} ^{[j]}(V,Q)=\operatorname {Cl} ^{[i+j]}(V,Q),}
其中方括號上標的運算模
2
{\displaystyle 2}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
Z
/
2
{\displaystyle \mathbb {Z} /2}
分次代數
C
l
[
0
]
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
子代數 偶子代數 。而子空間
C
l
[
1
]
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{[1]}(V,Q)}
奇部 (其不為子代數)。此
Z
/
2
{\displaystyle \mathbb {Z} /2}
α α -->
{\displaystyle \alpha }
主對合 (main involution)或次數對合 (grade involution)。此
Z
/
2
{\displaystyle \mathbb {Z} /2}
偶元 和奇元 。
當特徵非
2
{\displaystyle 2}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
N
{\displaystyle \mathbb {N} }
Z
{\displaystyle \mathbb {Z} }
[ d]
N
{\displaystyle \mathbb {N} }
Z
{\displaystyle \mathbb {Z} }
Z
/
2
{\displaystyle \mathbb {Z} /2}
Q
(
v
)
≠ ≠ -->
0
{\displaystyle Q(v)\neq 0}
v
∈ ∈ -->
C
l
1
(
V
,
Q
)
{\displaystyle v\in \mathrm {Cl} ^{1}(V,Q)}
v
2
∈ ∈ -->
C
l
0
(
V
,
Q
)
{\displaystyle v^{2}\in \mathrm {Cl} ^{0}(V,Q)}
C
l
2
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{2}(V,Q)}
Z
/
2
≅ ≅ -->
N
/
2
N
≅ ≅ -->
Z
/
2
Z
{\displaystyle \mathbb {Z} /2\cong \mathbb {N} /2\mathbb {N} \cong \mathbb {Z} /2\mathbb {Z} }
Z
{\displaystyle \mathbb {Z} }
濾過
Cl
⩽ ⩽ -->
i
-->
(
V
,
Q
)
⋅ ⋅ -->
Cl
⩽ ⩽ -->
j
-->
(
V
,
Q
)
⊂ ⊂ -->
Cl
⩽ ⩽ -->
i
+
j
-->
(
V
,
Q
)
.
{\displaystyle \operatorname {Cl} ^{\leqslant i}(V,Q)\cdot \operatorname {Cl} ^{\leqslant j}(V,Q)\subset \operatorname {Cl} ^{\leqslant i+j}(V,Q).}
克里福數的次數 通常指
N
{\displaystyle \mathbb {N} }
克里福代數的偶子代數
C
l
[
0
]
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}
[ e] [ f]
V
{\displaystyle V}
Q
(
a
)
{\displaystyle Q(a)}
a
{\displaystyle a}
U
{\displaystyle U}
C
l
[
0
]
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}
C
l
(
U
,
− − -->
Q
(
a
)
Q
)
{\displaystyle \mathrm {Cl} (U,-Q(a)Q)}
− − -->
Q
(
a
)
Q
{\displaystyle -Q(a)Q}
Q
{\displaystyle Q}
− − -->
Q
(
a
)
{\displaystyle -Q(a)}
U
{\displaystyle U}
Cl
p
,
q
[
0
]
-->
(
R
)
≅ ≅ -->
{
Cl
p
,
q
− − -->
1
-->
(
R
)
,
q
>
0
,
Cl
q
,
p
− − -->
1
-->
(
R
)
,
p
>
0.
{\displaystyle \operatorname {Cl} _{p,q}^{[0]}(\mathbb {R} )\cong {\begin{cases}\operatorname {Cl} _{p,q-1}(\mathbb {R} ),&q>0,\\\operatorname {Cl} _{q,p-1}(\mathbb {R} ),&p>0.\end{cases}}}
在
Q
{\displaystyle Q}
C
l
0
,
n
− − -->
1
(
R
)
⊂ ⊂ -->
C
l
0
,
n
(
R
)
{\displaystyle \mathrm {Cl} _{0,n-1}(\mathbb {R} )\subset \mathrm {Cl} _{0,n}(\mathbb {R} )}
R
⊂ ⊂ -->
C
⊂ ⊂ -->
H
⊂ ⊂ -->
H
⊕ ⊕ -->
H
⊂ ⊂ -->
⋯ ⋯ -->
{\displaystyle \mathbb {R} \subset \mathbb {C} \subset \mathbb {H} \subset \mathbb {H} \oplus \mathbb {H} \subset \cdots }
類似可證,在複域上,
C
l
n
(
C
)
{\displaystyle \mathrm {Cl} _{n}(\mathbb {C} )}
C
l
n
− − -->
1
(
C
)
{\displaystyle \mathrm {Cl} _{n-1}(\mathbb {C} )}
除自同構
α α -->
{\displaystyle \alpha }
反自同構 張量代數
T
(
V
)
{\displaystyle T(V)}
v
1
⊗ ⊗ -->
v
2
⊗ ⊗ -->
⋯ ⋯ -->
⊗ ⊗ -->
v
k
↦ ↦ -->
v
k
⊗ ⊗ -->
⋯ ⋯ -->
⊗ ⊗ -->
v
2
⊗ ⊗ -->
v
1
.
{\displaystyle v_{1}\otimes v_{2}\otimes \cdots \otimes v_{k}\mapsto v_{k}\otimes \cdots \otimes v_{2}\otimes v_{1}.}
由於理想
I
Q
{\displaystyle I_{Q}}
C
l
(
V
,
Q
)
≅ ≅ -->
T
(
V
)
/
I
Q
{\displaystyle \mathrm {Cl} (V,Q)\cong T(V)/I_{Q}}
轉置 或反轉 ,記為
x
↦ ↦ -->
x
t
{\displaystyle x\mapsto x^{\mathrm {t} }}
(
x
y
)
t
=
y
t
x
t
{\displaystyle (xy)^{\mathrm {t} }=y^{\mathrm {t} }x^{\mathrm {t} }}
Z
/
2
{\displaystyle \mathrm {Z} /2}
α α -->
{\displaystyle \alpha }
克里福共軛 ,記為
x
↦ ↦ -->
x
¯ ¯ -->
{\displaystyle x\mapsto {\overline {x}}}
x
¯ ¯ -->
=
α α -->
(
x
t
)
=
α α -->
(
x
)
t
.
{\displaystyle {\overline {x}}=\alpha (x^{\mathrm {t} })=\alpha (x)^{\mathrm {t} }.}
兩個反自同構中,轉置更本質。[ g]
此三種運算皆是對合 。此外,其對
Z
{\displaystyle \mathbb {Z} }
± ± -->
1
{\displaystyle \pm 1}
mod
4
{\displaystyle {\bmod {4}}}
x
{\displaystyle x}
k
{\displaystyle k}
α α -->
(
x
)
=
± ± -->
x
,
x
t
=
± ± -->
x
,
x
¯ ¯ -->
=
± ± -->
x
,
{\displaystyle \alpha (x)=\pm x,\qquad x^{\mathrm {t} }=\pm x,\qquad {\overline {x}}=\pm x,}
其中符號載於下表:
k
mod
4
{\displaystyle k{\bmod {4}}}
0
{\displaystyle 0}
1
{\displaystyle 1}
2
{\displaystyle 2}
3
{\displaystyle 3}
…
α α -->
(
x
)
{\displaystyle \alpha (x)\,}
+
{\displaystyle +}
− − -->
{\displaystyle -}
+
{\displaystyle +}
− − -->
{\displaystyle -}
(
− − -->
1
)
k
{\displaystyle (-1)^{k}}
x
t
{\displaystyle x^{\mathrm {t} }\,}
+
{\displaystyle +}
+
{\displaystyle +}
− − -->
{\displaystyle -}
− − -->
{\displaystyle -}
(
− − -->
1
)
k
(
k
− − -->
1
)
/
2
{\displaystyle (-1)^{k(k-1)/2}}
x
¯ ¯ -->
{\displaystyle {\overline {x}}}
+
{\displaystyle +}
− − -->
{\displaystyle -}
− − -->
{\displaystyle -}
+
{\displaystyle +}
(
− − -->
1
)
k
(
k
+
1
)
/
2
{\displaystyle (-1)^{k(k+1)/2}}
當特徴非
2
{\displaystyle 2}
V
{\displaystyle V}
Q
{\displaystyle Q}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
Q
{\displaystyle Q}
Q
(
x
)
=
⟨
x
t
x
⟩
0
,
{\displaystyle Q(x)=\left\langle x^{\mathrm {t} }x\right\rangle _{0},}
其中
⟨ ⟨ -->
a
⟩ ⟩ -->
0
{\displaystyle \langle a\rangle _{0}}
a
{\displaystyle a}
Z
{\displaystyle \mathbb {Z} }
V
{\displaystyle V}
v
i
{\displaystyle v_{i}}
Q
(
v
1
v
2
⋯ ⋯ -->
v
k
)
=
Q
(
v
1
)
Q
(
v
2
)
⋯ ⋯ -->
Q
(
v
k
)
,
{\displaystyle Q(v_{1}v_{2}\cdots v_{k})=Q(v_{1})Q(v_{2})\cdots Q(v_{k}),}
但上式對
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
在
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
Q
{\displaystyle Q}
⟨ ⟨ -->
x
,
y
⟩ ⟩ -->
=
⟨
x
t
y
⟩
0
.
{\displaystyle \langle x,y\rangle =\left\langle x^{\mathrm {t} }y\right\rangle _{0}.}
可以驗算,若限制在
V
{\displaystyle V}
V
{\displaystyle V}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
V
{\displaystyle V}
關於此純量積,左(右)乘
a
t
{\displaystyle a^{\mathrm {t} }}
a
{\displaystyle a}
伴隨 。換言之,
⟨ ⟨ -->
a
x
,
y
⟩ ⟩ -->
=
⟨
x
,
a
t
y
⟩
,
{\displaystyle \langle ax,y\rangle =\left\langle x,a^{\mathrm {t} }y\right\rangle ,}
且
⟨ ⟨ -->
x
a
,
y
⟩ ⟩ -->
=
⟨
x
,
y
a
t
⟩
.
{\displaystyle \langle xa,y\rangle =\left\langle x,ya^{\mathrm {t} }\right\rangle .}
本節假設域的特徵非
2
{\displaystyle 2}
V
{\displaystyle V}
Q
{\displaystyle Q}
中心 為
K
{\displaystyle K}
除代數
K
{\displaystyle K}
中心單代數
若
V
{\displaystyle V}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
K
{\displaystyle K}
若
V
{\displaystyle V}
C
l
[
0
]
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}
K
{\displaystyle K}
K
{\displaystyle K}
若
V
{\displaystyle V}
C
l
(
V
,
Q
)
{\displaystyle \mathrm {Cl} (V,Q)}
K
{\displaystyle K}
K
{\displaystyle K}
若
V
{\displaystyle V}
C
l
[
0
]
(
V
,
Q
)
{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}
K
{\displaystyle K}
克里福代數的結構可從以下結果推導出:假設
U
{\displaystyle U}
行列式 為
d
{\displaystyle d}
V
{\displaystyle V}
U
+
V
{\displaystyle U+V}
U
{\displaystyle U}
(
− − -->
1
)
dim
-->
(
U
)
/
2
d
V
{\displaystyle (-1)^{\dim(U)/2}dV}
V
{\displaystyle V}
(
− − -->
1
)
dim
-->
(
U
)
/
2
d
{\displaystyle (-1)^{\dim(U)/2}d}
Cl
p
+
2
,
q
-->
(
R
)
=
M
2
(
R
)
⊗ ⊗ -->
Cl
q
,
p
-->
(
R
)
{\displaystyle \operatorname {Cl} _{p+2,q}(\mathbb {R} )=\mathrm {M} _{2}(\mathbb {R} )\otimes \operatorname {Cl} _{q,p}(\mathbb {R} )}
Cl
p
+
1
,
q
+
1
-->
(
R
)
=
M
2
(
R
)
⊗ ⊗ -->
Cl
p
,
q
-->
(
R
)
{\displaystyle \operatorname {Cl} _{p+1,q+1}(\mathbb {R} )=\mathrm {M} _{2}(\mathbb {R} )\otimes \operatorname {Cl} _{p,q}(\mathbb {R} )}
Cl
p
,
q
+
2
-->
(
R
)
=
H
⊗ ⊗ -->
Cl
q
,
p
-->
(
R
)
.
{\displaystyle \operatorname {Cl} _{p,q+2}(\mathbb {R} )=\mathbb {H} \otimes \operatorname {Cl} _{q,p}(\mathbb {R} ).}
該些公式可用作找出所有實克里福代數和複克里福代數的結構,詳見克里福代數的分類
值得注意,克里福代數的森田等價 類(即其整個表示論:該代數上的模範疇 加性等價類 )只取決於其符號
(
p
− − -->
q
)
m
o
d
8
{\displaystyle (p-q)\ \mathrm {mod} \ 8}
博特周期性 。
利普希茨群(又稱為[ 4] :126 克里福群或克里福-利普希茨群)由魯道夫·利普希茨 發現。[ 6] :220
本節中,設
V
{\displaystyle V}
Q
{\displaystyle Q}
克里福代數的可逆元群 以「扭轉共軛」的方式作用 在克里福代數上:所謂
x
{\displaystyle x}
y
{\displaystyle y}
α α -->
(
x
)
y
x
− − -->
1
{\displaystyle \alpha (x)yx^{-1}}
α α -->
{\displaystyle \alpha }
上文 定義的主對合 。
利普希茨群
Γ Γ -->
{\displaystyle \Gamma }
α α -->
(
x
)
v
x
− − -->
1
∈ ∈ -->
V
∀ ∀ -->
v
∈ ∈ -->
V
{\displaystyle \alpha (x)vx^{-1}\in V\quad \forall v\in V}
的可逆元
x
{\displaystyle x}
x
{\displaystyle x}
穩定化 所有向量組成的集合。[ 9]
上式說明,該群作用可以限制成向量空間
V
{\displaystyle V}
Q
{\displaystyle Q}
正交群 的同態。利普希茨群包含所有令
Q
(
r
)
{\displaystyle Q(r)}
K
{\displaystyle K}
r
∈ ∈ -->
V
{\displaystyle r\in V}
V
{\displaystyle V}
v
↦ ↦ -->
v
− − -->
⟨ ⟨ -->
r
,
v
⟩ ⟩ -->
+
⟨ ⟨ -->
v
,
r
⟩ ⟩ -->
Q
(
r
)
r
.
{\displaystyle v\mapsto v-{\frac {\langle r,v\rangle +\langle v,r\rangle }{Q(r)}}r.}
(特徵為
2
{\displaystyle 2}
錯切 而非反射。)
若
V
{\displaystyle V}
非退化二次型
V
{\displaystyle V}
嘉當-迪厄多內定理 ),且核 恰好包含
K
{\displaystyle K}
短正合列
1
→ → -->
K
× × -->
→ → -->
Γ Γ -->
→ → -->
O
V
(
K
)
→ → -->
1
,
{\displaystyle 1\rightarrow K^{\times }\rightarrow \Gamma \rightarrow {\mbox{O}}_{V}(K)\rightarrow 1,\,}
1
→ → -->
K
× × -->
→ → -->
Γ Γ -->
0
→ → -->
SO
V
(
K
)
→ → -->
1.
{\displaystyle 1\rightarrow K^{\times }\rightarrow \Gamma ^{0}\rightarrow {\mbox{SO}}_{V}(K)\rightarrow 1.\,}
其中
Γ Γ -->
0
{\displaystyle \Gamma ^{0}}
Γ Γ -->
{\displaystyle \Gamma }
其他域上,或當二次型退化時,該映射未必滿,而旋量範數描述其不滿程度。
對任意特徵,利普希茨群上的旋量範數
Q
{\displaystyle Q}
Q
(
x
)
=
x
t
x
.
{\displaystyle Q(x)=x^{\mathrm {t} }x.}
其為由利普希茨群射去非零元素的乘法群
K
× × -->
{\displaystyle K^{\times }}
V
{\displaystyle V}
Q
{\displaystyle Q}
V
{\displaystyle V}
V
{\displaystyle V}
Γ Γ -->
1
{\displaystyle \Gamma ^{1}}
− − -->
1
{\displaystyle -1}
2
{\displaystyle 2}
− − -->
2
{\displaystyle -2}
2
{\displaystyle 2}
K
{\displaystyle K}
(
K
× × -->
)
2
{\displaystyle (K^{\times })^{2}}
V
{\displaystyle V}
V
{\displaystyle V}
K
× × -->
/
(
K
× × -->
)
2
{\displaystyle K^{\times }/(K^{\times })^{2}}
旋量範數 。對任意向量
r
{\displaystyle r}
r
⊥ ⊥ -->
{\displaystyle r^{\perp }}
⊥ ⊥ -->
{\displaystyle \perp }
K
× × -->
/
(
K
× × -->
)
2
{\displaystyle K^{\times }/(K^{\times })^{2}}
Q
(
r
)
{\displaystyle Q(r)}
1
→ → -->
{
± ± -->
1
}
→ → -->
Pin
V
(
K
)
→ → -->
O
V
(
K
)
→ → -->
K
× × -->
/
(
K
× × -->
)
2
,
1
→ → -->
{
± ± -->
1
}
→ → -->
Spin
V
(
K
)
→ → -->
SO
V
(
K
)
→ → -->
K
× × -->
/
(
K
× × -->
)
2
.
{\displaystyle {\begin{aligned}1\to \{\pm 1\}\to {\mbox{Pin}}_{V}(K)&\to {\mbox{O}}_{V}(K)\to K^{\times }/\left(K^{\times }\right)^{2},\\1\to \{\pm 1\}\to {\mbox{Spin}}_{V}(K)&\to {\mbox{SO}}_{V}(K)\to K^{\times }/\left(K^{\times }\right)^{2}.\end{aligned}}}
注意在特徵為
2
{\displaystyle 2}
{
± ± -->
1
}
{\displaystyle \{\pm 1\}}
若從代數群 的伽羅瓦上同調 考慮,旋量範數是上同調的連接同態 。其含義是,以
μ μ -->
2
{\displaystyle \mu _{2}}
1的平方根組成的代數群
2
{\displaystyle 2}
1
→ → -->
μ μ -->
2
→ → -->
Pin
V
→ → -->
O
V
→ → -->
1
{\displaystyle 1\to \mu _{2}\rightarrow {\mbox{Pin}}_{V}\rightarrow {\mbox{O}}_{V}\rightarrow 1}
給出上同調層面的長正合列 ,其起始一段為
1
→ → -->
H
0
(
μ μ -->
2
;
K
)
→ → -->
H
0
(
Pin
V
;
K
)
→ → -->
H
0
(
O
V
;
K
)
→ → -->
H
1
(
μ μ -->
2
;
K
)
→ → -->
⋯ ⋯ -->
{\displaystyle 1\to H^{0}(\mu _{2};K)\to H^{0}({\mbox{Pin}}_{V};K)\to H^{0}({\mbox{O}}_{V};K)\to H^{1}(\mu _{2};K)\to \cdots }
代數群的
K
{\displaystyle K}
K
{\displaystyle K}
H
0
(
G
;
K
)
=
G
(
K
)
{\displaystyle H^{0}(G;K)=G(K)}
H
1
(
μ μ -->
2
;
K
)
≅ ≅ -->
K
× × -->
/
(
K
× × -->
)
2
{\displaystyle H^{1}(\mu _{2};K)\cong K^{\times }/(K^{\times })^{2}}
1
→ → -->
{
± ± -->
1
}
→ → -->
Pin
V
(
K
)
→ → -->
O
V
(
K
)
→ → -->
K
× × -->
/
(
K
× × -->
)
2
,
{\displaystyle 1\to \{\pm 1\}\to {\mbox{Pin}}_{V}(K)\to {\mbox{O}}_{V}(K)\to K^{\times }/\left(K^{\times }\right)^{2},}
其中旋量範數為連接同態
H
0
(
O
V
;
K
)
→ → -->
H
1
(
μ μ -->
2
;
K
)
{\displaystyle H^{0}({\mbox{O}}_{V};K)\to H^{1}(\mu _{2};K)}
本節假設
V
{\displaystyle V}
Pin群
P
i
n
V
(
K
)
{\displaystyle \mathrm {Pin} _{V}(K)}
Γ Γ -->
{\displaystyle \Gamma }
1
{\displaystyle 1}
旋量群
S
p
i
n
V
(
K
)
{\displaystyle \mathrm {Spin} _{V}(K)}
P
i
n
V
(
K
)
{\displaystyle \mathrm {Pin} _{V}(K)}
迪克森不變量 為
0
{\displaystyle 0}
2
{\displaystyle 2}
1
{\displaystyle 1}
指數
2
{\displaystyle 2}
前一節說明,利普希茨群有到正交群的滿同態。定義特殊正交群
Γ Γ -->
0
{\displaystyle \Gamma ^{0}}
K
{\displaystyle K}
2
{\displaystyle 2}
1
{\displaystyle 1}
K
{\displaystyle K}
2
{\displaystyle 2}
1
{\displaystyle 1}
0
{\displaystyle 0}
也有從Pin群到正交群的同態。其像由旋量範數為
1
∈ ∈ -->
K
× × -->
/
(
K
× × -->
)
2
{\displaystyle 1\in K^{\times }/(K^{\times })^{2}}
+
1
{\displaystyle +1}
− − -->
1
{\displaystyle -1}
2
{\displaystyle 2}
2
{\displaystyle 2}
V
{\displaystyle V}
當
V
{\displaystyle V}
V
{\displaystyle V}
3
{\displaystyle 3}
單連通 。更甚者,此滿同態的核為
{
± ± -->
1
}
{\displaystyle \{\pm 1\}}
S
p
i
n
(
n
)
{\displaystyle \mathrm {Spin} (n)}
S
O
(
n
)
{\displaystyle \mathrm {SO} (n)}
V
{\displaystyle V}
R
p
,
q
{\displaystyle \mathbb {R} ^{p,q}}
p
,
q
{\displaystyle p,q}
2
{\displaystyle 2}
S
p
i
n
p
,
q
{\displaystyle \mathrm {Spin} _{p,q}}
S
p
i
n
p
,
q
(
R
)
{\displaystyle \mathrm {Spin} _{p,q}(\mathbb {R} )}
在
p
+
q
=
2
n
{\displaystyle p+q=2n}
C
l
p
,
q
(
C
)
{\displaystyle \mathrm {Cl} _{p,q}(\mathbb {C} )}
2
n
{\displaystyle 2^{n}}
P
i
n
p
,
q
(
R
)
{\displaystyle \mathrm {Pin} _{p,q}(\mathbb {R} )}
旋量表示
S
p
i
n
p
,
q
(
R
)
{\displaystyle \mathrm {Spin} _{p,q}(\mathbb {R} )}
半旋量表示 (half spin representations,又稱外爾表示 ,Weyl representations)的直和,每個半旋量表示有
2
n
− − -->
1
{\displaystyle 2^{n-1}}
若
p
+
q
=
2
n
+
1
{\displaystyle p+q=2n+1}
C
l
p
,
q
(
C
)
{\displaystyle \mathrm {Cl} _{p,q}(\mathbb {C} )}
2
n
{\displaystyle 2^{n}}
P
i
n
p
,
q
(
R
)
{\displaystyle \mathrm {Pin} _{p,q}(\mathbb {R} )}
S
p
i
n
p
,
q
(
R
)
{\displaystyle \mathrm {Spin} _{p,q}(\mathbb {R} )}
2
n
{\displaystyle 2^{n}}
更一般而言,任何域上的旋量群和Pin群都有相似的表示,其結構取決於對應的克里福代數的結構 旋量 條目。
為描述實旋量表示,需先明白旋量群如何位處克里福代數中。Pin群
P
i
n
p
,
q
{\displaystyle \mathrm {Pin} _{p,q}}
C
l
p
,
q
{\displaystyle \mathrm {Cl} _{p,q}}
P
i
n
p
,
q
=
{
v
1
v
2
⋯ ⋯ -->
v
r
∣ ∣ -->
∀ ∀ -->
i
,
‖ ‖ -->
v
i
‖ ‖ -->
=
± ± -->
1
}
.
{\displaystyle \mathrm {Pin} _{p,q}=\left\{v_{1}v_{2}\cdots v_{r}\mid \forall i,\ \|v_{i}\|=\pm 1\right\}.}
若考慮克里福代數的矩陣表示,則pin群的元素為任意多個反射(見上文 )之積,是整個正交群
O
(
p
,
q
)
{\displaystyle \mathrm {O} (p,q)}
旋量群 的元素則是
P
i
n
p
,
q
{\displaystyle \mathrm {Pin} _{p,q}}
嘉當-迪厄多內定理 ,旋量群是旋轉群
S
O
(
p
,
q
)
{\displaystyle \mathrm {SO} (p,q)}
設
α α -->
:
C
l
→ → -->
C
l
{\displaystyle \alpha :\mathrm {Cl} \to \mathrm {Cl} }
v
{\displaystyle v}
− − -->
v
{\displaystyle -v}
S
p
i
n
p
,
q
{\displaystyle \mathrm {Spin} _{p,q}}
P
i
n
p
,
q
{\displaystyle \mathrm {Pin} _{p,q}}
α α -->
{\displaystyle \alpha }
Cl
p
,
q
[
0
]
=
{
x
∈ ∈ -->
Cl
p
,
q
∣ ∣ -->
α α -->
(
x
)
=
x
}
.
{\displaystyle \operatorname {Cl} _{p,q}^{[0]}=\{x\in \operatorname {Cl} _{p,q}\mid \alpha (x)=x\}.}
(其元素正是
C
l
p
,
q
{\displaystyle \mathrm {Cl} _{p,q}}
C
l
p
,
q
[
0
]
{\displaystyle \mathrm {Cl} _{p,q}^{[0]}}
C
l
p
,
q
{\displaystyle \mathrm {Cl} _{p,q}}
不可約表示 可以限制 導出
C
l
p
,
q
[
0
]
{\displaystyle \mathrm {Cl} _{p,q}^{[0]}}
要將pin群的表示分類,需要用到克里福代數的分類 上文 ):
Cl
p
,
q
[
0
]
≅ ≅ -->
Cl
p
,
q
− − -->
1
,
q
>
0
,
{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{p,q-1},\quad q>0,}
Cl
p
,
q
[
0
]
≅ ≅ -->
Cl
q
,
p
− − -->
1
,
p
>
0
,
{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{q,p-1},\quad p>0,}
從而得知,符號
(
p
,
q
)
{\displaystyle (p,q)}
(
p
,
q
− − -->
1
)
{\displaystyle (p,q-1)}
(
q
,
p
− − -->
1
)
{\displaystyle (q,p-1)}
外代數在微分幾何 可用作定義光滑流形 上的微分形式 叢 。在(偽 )黎曼流形 的情況,每個切空間 上配備自然的二次型(由度規張量 導出)。所以,如同外叢 克里福叢 黎曼幾何 ,克里福叢有若干重要應用,例如其與旋量流形 旋量叢 、
S
p
i
n
C
{\displaystyle \mathrm {Spin} ^{\mathbb {C} }}
克里福代數在物理有若干重要應用。物理學家通常認定克里福代數具有一組基,其由狄拉克矩陣
γ γ -->
0
,
… … -->
,
γ γ -->
3
{\displaystyle \gamma _{0},\ldots ,\gamma _{3}}
γ γ -->
i
γ γ -->
j
+
γ γ -->
j
γ γ -->
i
=
2
η η -->
i
j
{\displaystyle \gamma _{i}\gamma _{j}+\gamma _{j}\gamma _{i}=2\eta _{ij}\,}
其中
η η -->
{\displaystyle \eta }
(
1
,
3
)
{\displaystyle (1,3)}
(
3
,
1
)
{\displaystyle (3,1)}
C
l
1
,
3
(
R
)
{\displaystyle \mathrm {Cl} _{1,3}(\mathbb {R} )}
複化
C
l
1
,
3
(
R
)
C
{\displaystyle \mathrm {Cl} _{1,3}(\mathbb {R} )_{\mathbb {C} }}
克里福代數的分類
4
× × -->
4
{\displaystyle 4\times 4}
C
l
4
(
C
)
≅ ≅ -->
M
4
(
C
)
{\displaystyle \mathrm {Cl} _{4}(\mathbb {C} )\cong \mathrm {M} _{4}(\mathbb {C} )}
C
l
1
,
3
(
R
)
C
{\displaystyle \mathrm {Cl} _{1,3}(\mathbb {R} )_{\mathbb {C} }}
洛伦兹变换 。
所以,物理使用的時空克里福代數比
C
l
4
(
C
)
{\displaystyle \mathrm {Cl} _{4}(\mathbb {C} )}
李代數
s
o
(
1
,
3
)
{\displaystyle {\mathfrak {so}}(1,3)}
旋量表示
σ σ -->
μ μ -->
ν ν -->
=
− − -->
i
4
[
γ γ -->
μ μ -->
,
γ γ -->
ν ν -->
]
,
[
σ σ -->
μ μ -->
ν ν -->
,
σ σ -->
ρ ρ -->
τ τ -->
]
=
i
(
η η -->
τ τ -->
μ μ -->
σ σ -->
ρ ρ -->
ν ν -->
+
η η -->
ν ν -->
τ τ -->
σ σ -->
μ μ -->
ρ ρ -->
− − -->
η η -->
ρ ρ -->
μ μ -->
σ σ -->
τ τ -->
ν ν -->
− − -->
η η -->
ν ν -->
ρ ρ -->
σ σ -->
μ μ -->
τ τ -->
)
.
{\displaystyle {\begin{aligned}\sigma ^{\mu \nu }&=-{\frac {i}{4}}\left[\gamma ^{\mu },\,\gamma ^{\nu }\right],\\\left[\sigma ^{\mu \nu },\,\sigma ^{\rho \tau }\right]&=i\left(\eta ^{\tau \mu }\sigma ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^{\nu \rho }\sigma ^{\mu \tau }\right).\end{aligned}}}
上式按照
(
3
,
1
)
{\displaystyle (3,1)}
C
l
3
,
1
(
R
)
C
{\displaystyle \mathrm {Cl} _{3,1}(\mathbb {R} )_{\mathbb {C} }}
[ 10]
狄拉克矩陣最早由保罗·狄拉克 寫出,其時他正嘗試寫出電子 的相對論性一階波動方程,並試圖給出由克里福代數到複矩陣代數的明確同構。該些矩陣後來用作定義狄拉克方程式 和引入狄拉克算子 。在量子場論 中,整個克里福代數以Dirac field bilinear
使用克里福代數來描述量子理論,推動者有Mario Schönberg [ h] David Hestenes 幾何微積分 戴维·玻姆 和Basil Hiley 克里福代數的分層 [ 11] [ 12]
電腦視覺 方面,克里福代數適用於辨認和分類動作。米基·洛迪古斯(Mikel Rodriguez)及合作者[ 13] M aximum A verage C orrelation H eight filter, MACH filter)推廣,套用於影片(3D時空體積)以及向量值數據,例如光流 。向量值數據需以克里福傅立葉變換
本條目只考慮域上的向量空間的克里福代數,但同樣可定義任何單位結合交換環上的模 的克里福代數。[ 3]
亦在克里福代數的定義中,將二次型推廣成更高次的映射。[ 14]
克里福代數和幾何代數,以及相關的跨學科研究,是活躍的研究主題,且有廣泛的應用。此學科的學術會議包括克里福代數及其在數學物理的應用國際會議(ICCA) (页面存档备份 ,存于互联网档案馆 )及幾何代數在電腦科學及工程學的應用(AGACSE) (页面存档备份 ,存于互联网档案馆 )兩個系列。期刊包括斯普林格 出版的《應用克里福代數進展
^ 研究實克里福代數且偏好正定二次型者(尤其研究指標理論 者),有時在基本克里福恆等式中使用不同的符號
v
2
=
− − -->
Q
(
v
)
{\displaystyle v^{2}=-Q(v)}
Q
{\displaystyle Q}
− − -->
Q
{\displaystyle -Q}
^ [ 4]
i
{\displaystyle i}
γ γ -->
{\displaystyle \gamma }
(
A
,
γ γ -->
)
{\displaystyle (A,\gamma )}
(
V
,
g
)
{\displaystyle (V,g)}
A
{\displaystyle A}
{
γ γ -->
(
v
)
|
v
∈ ∈ -->
V
}
{\displaystyle \{\gamma ({\boldsymbol {v}})|{\boldsymbol {v}}\in V\}}
{
a
1
A
|
a
∈ ∈ -->
R
}
{\displaystyle \{a1_{A}|a\in \mathbb {R} \}}
γ γ -->
{\displaystyle \gamma }
v
,
u
∈ ∈ -->
V
{\displaystyle {\boldsymbol {v}},{\boldsymbol {u}}\in V}
γ γ -->
(
v
)
γ γ -->
(
u
)
+
γ γ -->
(
u
)
γ γ -->
(
v
)
=
2
g
(
v
,
u
)
{\displaystyle \gamma ({\boldsymbol {v}})\gamma ({\boldsymbol {u}})+\gamma ({\boldsymbol {u}})\gamma ({\boldsymbol {v}})=2g({\boldsymbol {v}},{\boldsymbol {u}})}
^ 故群代數
K
[
Z
/
2
]
{\displaystyle K[\mathbb {Z} /2]}
半單 特徵空間 。
^ 此處的
Z
{\displaystyle \mathbb {Z} }
∧ ∧ -->
(
V
)
{\displaystyle \wedge (V)}
N
{\displaystyle \mathbb {N} }
^ 嚴格而言,因為未指明克里福代數定義中的向量空間,所以該同構僅是代數同構,而非克里福代數同構。
^ 仍假設特徵非
2
{\displaystyle 2}
^ 若在克里福代數的定義中,約定的符號不同(多一個負號),則反之,即共軛更本質。一般而言,共軛與轉置的含義會因約定的符號不同而互換。例如,本條目採用的定義中,向量的逆元為
v
− − -->
1
=
v
t
/
Q
(
v
)
{\displaystyle v^{-1}=v^{\mathrm {t} }/Q(v)}
v
− − -->
1
=
v
¯ ¯ -->
/
Q
(
v
)
{\displaystyle v^{-1}={\overline {v}}/Q(v)}
^ 見A. O. Bolivar,
Classical limit of fermions in phase space, J. Math. Phys. 42, 4020 (2001) doi :10.1063/1.1386411 在"The Grassmann–Schönberg algebra
G
n
{\displaystyle G_{n}}
^ Clifford, W.K. Preliminary sketch of bi-quaternions. Proc. London Math. Soc. 1873, 4 : 381–395 (英语) . ^ Clifford, W.K. Tucker, R. , 编. Mathematical Papers . London: Macmillan. 1882 (英语) . ^ 3.0 3.1 Oziewicz, Z.; Sitarczyk, Sz. Parallel treatment of Riemannian and symplectic Clifford algebras . Micali, A.; Boudet, R.; Helmstetter, J. (编). Clifford Algebras and their Applications in Mathematical Physics. Kluwer. 1992: 83 [2021-08-05 ] . ISBN 0-7923-1623-1存档 于2021-08-05) (英语) . ^ 4.0 4.1 Vaz, J.; da Rocha, R., An Introduction to Clifford Algebras and Spinors, Oxford University Press , 2016, ISBN 978-0-19-878292-6(英语)
^ P. Lounesto, Counterexamples in Clifford algebras with CLICAL, Clifford Algebras with Numeric and Symbolic Computations, 1996: 3–30, ISBN 978-1-4615-8159-8doi:10.1007/978-1-4615-8157-4_1 (英语) 刪節版 (页面存档备份 ,存于互联网档案馆 )^ 6.0 6.1 Lounesto, Pertti, Clifford algebras and spinors, Cambridge University Press , 2001, ISBN 978-0-521-00551-7doi:10.1017/CBO9780511526022 (英语) ^ McCarthy, J.M. An Introduction to Theoretical Kinematics . MIT Press. 1990: 62–65 [2021-08-06 ] . ISBN 978-0-262-13252-7存档 于2021-08-06) (英语) . ^ Bottema, O.; Roth, B. Theoretical Kinematics . Dover. 2012 [1979] [2021-08-06 ] . ISBN 978-0-486-66346-3存档 于2021-08-06) (英语) . ^ Perwass, Christian, Geometric Algebra with Applications in Engineering, Springer Science & Business Media, 2009, Bibcode:2009gaae.book.....P ISBN 978-3-540-89068-3(英语) ^ Weinberg, S. , The Quantum Theory of Fields 1 , Cambridge University Press , 2002, ISBN 0-521-55001-7(英语) ^ Conte, Elio. A Quantum-Like Interpretation and Solution of Einstein, Podolsky, and Rosen Paradox in Quantum Mechanics. 14 Nov 2007. arXiv:0711.2260 quant-ph ] (英语) . ^ Conte, Elio. On some considerations of mathematical physics: May we identify Clifford algebra as a common algebraic structure for classical diffusion and Schrödinger equations?. Adv. Studies Theor. Phys. 2012, 6 (26): 1289–1307 (英语) . ^ Rodriguez, Mikel; Shah, M. Action MACH: A Spatio-Temporal Maximum Average Correlation Height Filter for Action Classification. Computer Vision and Pattern Recognition (CVPR). 2008 (英语) . ^
Darrell E. Haile. On the Clifford Algebra of a Binary Cubic Form . American Journal of Mathematics (The Johns Hopkins University Press). Dec 1984, 106 (6): 1269–1280. JSTOR 2374394 doi:10.2307/2374394 (英语) .





























































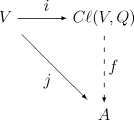
























































![{\displaystyle \mathrm {Cl} _{0,3}^{[0]}(\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6541725197b4f192001bd32ca1cf8b678d576da5)

















![{\displaystyle \mathrm {Cl} ^{[0]}(\mathbb {R} ^{4},d)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99eff326ee15b18fc9a58606715d26fb85642933)









![{\displaystyle K[x]/(x^{2}-a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c62c3e9a4da297f0a0758ff5849fbfe553242cc)





































![{\displaystyle \operatorname {Cl} (V,Q)=\operatorname {Cl} ^{[0]}(V,Q)\oplus \operatorname {Cl} ^{[1]}(V,Q),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f839fb22e8ff47a3cd64ae06d9a6338584ff0a5)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)=\left\{x\in \operatorname {Cl} (V,Q)\mid \alpha (x)=(-1)^{i}x\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6902ed1e7c0361df4271000a56e7b76c029990e)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)\operatorname {Cl} ^{[j]}(V,Q)=\operatorname {Cl} ^{[i+j]}(V,Q),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25f34257a1d5cb5d629f65bf4806f4644ce0fb33)
![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754)
![{\displaystyle \mathrm {Cl} ^{[1]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f04cddd1b4026240bc7face04ef5d2c4f25639a)













![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}(\mathbb {R} )\cong {\begin{cases}\operatorname {Cl} _{p,q-1}(\mathbb {R} ),&q>0,\\\operatorname {Cl} _{q,p-1}(\mathbb {R} ),&p>0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f26b903ab34e6843840ad77e22c9789d7e1cf97d)























































































![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}=\{x\in \operatorname {Cl} _{p,q}\mid \alpha (x)=x\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e214b8b455c0610747a107adad00e2c3573ca61)
![{\displaystyle \mathrm {Cl} _{p,q}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50aac8d6b975f2c3da4d598216e6b5082f83ed08)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{p,q-1},\quad q>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f577d7e3b1ee705c0a49d4cc02bc3c4a500cd83f)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{q,p-1},\quad p>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f54de96cfa5fa50cc445b55dfeba1ebca01991)














![{\displaystyle {\begin{aligned}\sigma ^{\mu \nu }&=-{\frac {i}{4}}\left[\gamma ^{\mu },\,\gamma ^{\nu }\right],\\\left[\sigma ^{\mu \nu },\,\sigma ^{\rho \tau }\right]&=i\left(\eta ^{\tau \mu }\sigma ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^{\nu \rho }\sigma ^{\mu \tau }\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5881264248f2f1787c4d1d2c4de84dd1678754)










![{\displaystyle K[\mathbb {Z} /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5a75e48de8b88ea9f7f75bc179a736ff80e9fde)



