–Ґ—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–ЄћБ—З–љ—Ц —Д—ГћБ–љ–Ї—Ж—Ц—Ч вАФ —Д—Г–љ–Ї—Ж—Ц—Ч –Ї—Г—В–∞ . –Т–Њ–љ–Є –Љ–Њ–ґ—Г—В—М –±—Г—В–Є –≤–Є–Ј–љ–∞—З–µ–љ—Ц —П–Ї –≤—Ц–і–љ–Њ—И–µ–љ–љ—П –і–≤–Њ—Е —Б—В–Њ—А—Ц–љ —В–∞ –Ї—Г—В–∞ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ –∞–±–Њ —П–Ї –≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Ї–Њ–Њ—А–і–Є–љ–∞—В —В–Њ—З–Њ–Ї –Ї–Њ–ї–∞. –Т—Ц–і—Ц–≥—А–∞—О—В—М –≤–∞–ґ–ї–Є–≤—Г —А–Њ–ї—М –њ—А–Є –і–Њ—Б–ї—Ц–і–ґ–µ–љ–љ—Ц –њ–µ—А—Ц–Њ–і–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є —В–∞ –±–∞–≥–∞—В—М–Њ—Е –Њ–±'—Ф–Ї—В—Ц–≤. –Э–∞–њ—А–Є–Ї–ї–∞–і, –њ—А–Є –і–Њ—Б–ї—Ц–і–ґ–µ–љ–љ—Ц —А—П–і—Ц–≤ , –і–Є—Д–µ—А–µ–љ—Ж—Ц–∞–ї—М–љ–Є—Е —А—Ц–≤–љ—П–љ—М .
–Э–∞–≤–µ–і–µ–Љ–Њ —И—Ц—Б—В—М –±–∞–Ј–Њ–≤–Є—Е —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є. –Ю—Б—В–∞–љ–љ—Ц —З–Њ—В–Є—А–Є –≤–Є–Ј–љ–∞—З–∞—О—В—М—Б—П —З–µ—А–µ–Ј –њ–µ—А—И—Ц –і–≤—Ц. –Ж–љ—И–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –≤–Њ–љ–Є —Ф –Њ–Ј–љ–∞—З–µ–љ–љ—П–Љ–Є, –∞ –љ–µ —Б–∞–Љ–Њ—Б—В—Ц–є–љ–Є–Љ–Є —Б—Г—В–љ–Њ—Б—В—П–Љ–Є.
—Б–Є–љ—Г—Б (
sin
вБ° -->
α ќ± -->
{\displaystyle \sin \alpha }
–Ї–Њ—Б–Є–љ—Г—Б (
cos
вБ° -->
α ќ± -->
{\displaystyle \cos \alpha }
—В–∞–љ–≥–µ–љ—Б (
tg
вБ° -->
α ќ± -->
=
sin
вБ° -->
α ќ± -->
cos
вБ° -->
α ќ± -->
{\displaystyle \operatorname {tg} \alpha ={\tfrac {\sin \alpha }{\cos \alpha }}}
–Ї–Њ—В–∞–љ–≥–µ–љ—Б (
ctg
вБ° -->
α ќ± -->
=
cos
вБ° -->
α ќ± -->
sin
вБ° -->
α ќ± -->
{\displaystyle \operatorname {ctg} \alpha ={\tfrac {\cos \alpha }{\sin \alpha }}}
—Б–µ–Ї–∞–љ—Б (
sec
вБ° -->
α ќ± -->
=
1
cos
вБ° -->
α ќ± -->
{\displaystyle \sec \alpha ={\tfrac {1}{\cos \alpha }}}
–Ї–Њ—Б–µ–Ї–∞–љ—Б (
cosec
вБ° -->
α ќ± -->
=
1
sin
вБ° -->
α ќ± -->
{\displaystyle \operatorname {cosec} \alpha ={\tfrac {1}{\sin \alpha }}}
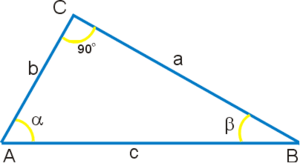
–Т–Є–Ј–љ–∞—З–µ–љ–љ—П –Ї—Г—В—Ц–≤ –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. –Т–Є–Ј–љ–∞—З–µ–љ–љ—П —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є –љ–∞ –Њ–і–Є–љ–Є—З–љ–Њ–Љ—Г –Ї–Њ–ї—Ц. –Ґ—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч –Љ–Њ–ґ–љ–∞ –≤–Є–Ј–љ–∞—З–Є—В–Є —А–Њ–Ј–≥–ї—П–љ—Г–≤—И–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї . –Ї–∞—В–µ—В–∞ –і–Њ –і–Њ–≤–ґ–Є–љ–Є –≥—Ц–њ–Њ—В–µ–љ—Г–Ј–Є :
cos
вБ° -->
α ќ± -->
=
A
C
A
B
=
b
c
,
cos
вБ° -->
β ќ≤ -->
=
B
C
A
B
=
a
c
.
{\displaystyle \cos \alpha ={\frac {AC}{AB}}={\frac {b}{c}},~~~\cos \beta ={\frac {BC}{AB}}={\frac {a}{c}}~.}
–°–Є–љ—Г—Б–Њ–Љ –Ї—Г—В–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –≤—Ц–і–љ–Њ—И–µ–љ–љ—П –і–Њ–≤–ґ–Є–љ–Є –њ—А–Њ—В–Є–ї–µ–ґ–љ–Њ–≥–Њ –Ї–∞—В–µ—В–∞ –і–Њ –і–Њ–≤–ґ–Є–љ–Є –≥—Ц–њ–Њ—В–µ–љ—Г–Ј–Є:
sin
вБ° -->
α ќ± -->
=
B
C
A
B
=
a
c
,
sin
вБ° -->
β ќ≤ -->
=
A
C
A
B
=
b
c
.
{\displaystyle \sin \alpha ={\frac {BC}{AB}}={\frac {a}{c}},~~~\sin \beta ={\frac {AC}{AB}}={\frac {b}{c}}~.}
–Ґ–∞–љ–≥–µ–љ—Б–Њ–Љ –Ї—Г—В–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –≤—Ц–і–љ–Њ—И–µ–љ–љ—П –і–Њ–≤–ґ–Є–љ–Є –њ—А–Њ—В–Є–ї–µ–ґ–љ–Њ–≥–Њ –Ї–∞—В–µ—В–∞ –і–Њ –і–Њ–≤–ґ–Є–љ–Є –њ—А–Є–ї–µ–≥–ї–Њ–≥–Њ –Ї–∞—В–µ—В–∞:
tg
вБ° -->
α ќ± -->
=
B
C
A
C
=
a
b
,
tg
вБ° -->
β ќ≤ -->
=
A
C
B
C
=
b
a
.
{\displaystyle \operatorname {tg} \alpha ={\frac {BC}{AC}}={\frac {a}{b}},~~~\operatorname {tg} \beta ={\frac {AC}{BC}}={\frac {b}{a}}~.}
–Ъ–Њ—В–∞–љ–≥–µ–љ—Б–Њ–Љ –Ї—Г—В–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –≤—Ц–і–љ–Њ—И–µ–љ–љ—П –і–Њ–≤–ґ–Є–љ–Є –њ—А–Є–ї–µ–≥–ї–Њ–≥–Њ –Ї–∞—В–µ—В–∞ –і–Њ –і–Њ–≤–ґ–Є–љ–Є –њ—А–Њ—В–Є–ї–µ–ґ–љ–Њ–≥–Њ –Ї–∞—В–µ—В–∞:
ctg
вБ° -->
α ќ± -->
=
A
C
B
C
=
b
a
,
ctg
вБ° -->
β ќ≤ -->
=
B
C
A
C
=
a
b
.
{\displaystyle \operatorname {ctg} \alpha ={\frac {AC}{BC}}={\frac {b}{a}},~~~\operatorname {ctg} \beta ={\frac {BC}{AC}}={\frac {a}{b}}~.}
–Р–љ–∞–ї–Њ–≥—Ц—З–љ–Є–Љ —З–Є–љ–Њ–Љ –Љ–Њ–ґ–љ–∞ –≤–Є–Ј–љ–∞—З–Є—В–Є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч –љ–∞ –Ї–Њ–ї—Ц –Ј –Њ–і–Є–љ–Є—З–љ–Є–Љ —А–∞–і—Ц—Г—Б–Њ–Љ.
–Ю–і–Є–љ –њ–µ—А—Ц–Њ–і —Д—Г–љ–Ї—Ж—Ц–є
sin
вБ° -->
x
{\displaystyle \sin x}
cos
вБ° -->
x
{\displaystyle \cos x}
sin
вБ° -->
x
{\displaystyle \sin x}
cos
вБ° -->
x
{\displaystyle \cos x}
–њ–µ—А—Ц–Њ–і–Є—З–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч —Ц–Ј –њ–µ—А—Ц–Њ–і–Њ–Љ
2
π ѕА -->
{\displaystyle \ 2\pi }
tg
вБ° -->
x
{\displaystyle \operatorname {tg} x}
ctg
вБ° -->
x
{\displaystyle \operatorname {ctg} x}
π ѕА -->
.
{\displaystyle \ \pi .}
–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П, –љ–∞–≤–µ–і–µ–љ—Ц –љ–Є–ґ—З–µ, –і–Њ–Ј–≤–Њ–ї—П—О—В—М –≤–Є—А–∞–Ј–Є—В–Є –Ј–љ–∞—З–µ–љ–љ—П —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є –≤—Ц–і –і–Њ–≤—Ц–ї—М–љ–Њ–≥–Њ –і—Ц–є—Б–љ–Њ–≥–Њ –∞—А“С—Г–Љ–µ–љ—В—Г —З–µ—А–µ–Ј –Ј–љ–∞—З–µ–љ–љ—П —Д—Г–љ–Ї—Ж—Ц–є –і–ї—П –∞—А–≥—Г–Љ–µ–љ—В—Г –Ј —Ц–љ—В–µ—А–≤–∞–ї—Г
[
0
,
π ѕА -->
2
]
{\displaystyle \left[0,{\pi \over 2}\right]}
sin
вБ° -->
x
=
cos
вБ° -->
(
π ѕА -->
2
− вИТ -->
x
)
{\displaystyle \sin x=\cos \left({\pi \over 2}-x\right)}
cos
вБ° -->
x
=
sin
вБ° -->
(
π ѕА -->
2
− вИТ -->
x
)
{\displaystyle \cos x=\sin \left({\pi \over 2}-x\right)}
tg
вБ° -->
x
=
ctg
вБ° -->
(
π ѕА -->
2
− вИТ -->
x
)
{\displaystyle \operatorname {tg} x=\operatorname {ctg} \left({\pi \over 2}-x\right)}
ctg
вБ° -->
x
=
tg
вБ° -->
(
π ѕА -->
2
− вИТ -->
x
)
{\displaystyle \operatorname {ctg} x=\operatorname {tg} \left({\pi \over 2}-x\right)}
–Э–∞—Б—В—Г–њ–љ–µ —Б–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –≤–Є–њ–ї–Є–≤–∞—Ф —Ц–Ј —В–µ–Њ—А–µ–Љ–Є –Я—Ц—Д–∞–≥–Њ—А–∞ :
sin
2
вБ° -->
x
+
cos
2
вБ° -->
x
=
1
{\displaystyle ~\sin ^{2}x+\cos ^{2}x=1}
–Ч –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ —Б–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П
sin
вБ° -->
(
α ќ± -->
+
β ќ≤ -->
)
=
sin
вБ° -->
α ќ± -->
cos
вБ° -->
β ќ≤ -->
+
cos
вБ° -->
α ќ± -->
sin
вБ° -->
β ќ≤ -->
{\displaystyle \sin {\left(\alpha +\beta \right)}=\sin \alpha \cos \beta +\cos \alpha \sin \beta }
–Њ—В—А–Є–Љ—Г—Ф–Љ–Њ
sin
вБ° -->
(
α ќ± -->
± ¬± -->
β ќ≤ -->
)
=
sin
вБ° -->
α ќ± -->
cos
вБ° -->
β ќ≤ -->
± ¬± -->
cos
вБ° -->
α ќ± -->
sin
вБ° -->
β ќ≤ -->
,
{\displaystyle \sin {\left(\alpha \pm \beta \right)}=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta ,}
cos
вБ° -->
(
α ќ± -->
± ¬± -->
β ќ≤ -->
)
=
cos
вБ° -->
α ќ± -->
cos
вБ° -->
β ќ≤ -->
∓ вИУ -->
sin
вБ° -->
α ќ± -->
sin
вБ° -->
β ќ≤ -->
,
{\displaystyle \cos {\left(\alpha \pm \beta \right)}=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta ,}
tg
вБ° -->
(
α ќ± -->
± ¬± -->
β ќ≤ -->
)
=
tg
вБ° -->
α ќ± -->
± ¬± -->
tg
вБ° -->
β ќ≤ -->
1
∓ вИУ -->
tg
вБ° -->
α ќ± -->
tg
вБ° -->
β ќ≤ -->
,
ctg
вБ° -->
(
α ќ± -->
± ¬± -->
β ќ≤ -->
)
=
ctg
вБ° -->
α ќ± -->
ctg
вБ° -->
β ќ≤ -->
∓ вИУ -->
1
ctg
вБ° -->
β ќ≤ -->
± ¬± -->
ctg
вБ° -->
α ќ± -->
{\displaystyle \operatorname {tg} {\left(\alpha \pm \beta \right)}={{\operatorname {tg} \alpha \pm \operatorname {tg} \beta } \over {1\mp \operatorname {tg} \alpha \operatorname {tg} \beta }},~~~\operatorname {ctg} {\left(\alpha \pm \beta \right)}={{\operatorname {ctg} \alpha \operatorname {ctg} \beta \mp 1} \over {\operatorname {ctg} \beta \pm \operatorname {ctg} \alpha }}}
sin
вБ° -->
2
α ќ± -->
=
2
sin
вБ° -->
α ќ± -->
cos
вБ° -->
α ќ± -->
{\displaystyle \sin {2\alpha }=2\sin \alpha \cos \alpha }
cos
вБ° -->
2
α ќ± -->
=
cos
2
вБ° -->
α ќ± -->
− вИТ -->
sin
2
вБ° -->
α ќ± -->
=
2
cos
2
вБ° -->
α ќ± -->
− вИТ -->
1
=
1
− вИТ -->
2
sin
2
вБ° -->
α ќ± -->
{\displaystyle \cos {2\alpha }=\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha }
tg
вБ° -->
2
α ќ± -->
=
2
tg
вБ° -->
α ќ± -->
1
− вИТ -->
tg
2
вБ° -->
α ќ± -->
,
ctg
вБ° -->
2
α ќ± -->
=
ctg
2
вБ° -->
α ќ± -->
− вИТ -->
1
2
ctg
вБ° -->
α ќ± -->
=
1
2
(
ctg
вБ° -->
α ќ± -->
− вИТ -->
tg
вБ° -->
α ќ± -->
)
{\displaystyle \operatorname {tg} {2\alpha }={{2\operatorname {tg} \alpha } \over {1-\operatorname {tg} ^{2}\alpha }}~,~~~\operatorname {ctg} {2\alpha }={{\operatorname {ctg} ^{2}\alpha -1} \over {2\operatorname {ctg} \alpha }}={1 \over 2}{\left(\operatorname {ctg} \alpha -\operatorname {tg} \alpha \right)}}
sin
вБ° -->
3
α ќ± -->
=
3
sin
вБ° -->
α ќ± -->
− вИТ -->
4
sin
3
вБ° -->
α ќ± -->
,
cos
вБ° -->
3
α ќ± -->
=
4
cos
3
вБ° -->
α ќ± -->
− вИТ -->
3
cos
вБ° -->
α ќ± -->
{\displaystyle \sin {3\alpha }=3\sin \alpha -4\sin ^{3}\alpha ~,~~~\cos {3\alpha }=4\cos ^{3}\alpha -3\cos \alpha }
sin
вБ° -->
α ќ± -->
2
=
1
− вИТ -->
cos
вБ° -->
α ќ± -->
2
,
cos
вБ° -->
α ќ± -->
2
=
1
+
cos
вБ° -->
α ќ± -->
2
{\displaystyle \sin {\alpha \over 2}={\sqrt {{1-\cos \alpha } \over 2}}~,~~~\cos {\alpha \over 2}={\sqrt {{1+\cos \alpha } \over 2}}}
tg
вБ° -->
α ќ± -->
2
=
sin
вБ° -->
α ќ± -->
1
+
cos
вБ° -->
α ќ± -->
=
1
− вИТ -->
cos
вБ° -->
α ќ± -->
sin
вБ° -->
α ќ± -->
,
ctg
вБ° -->
α ќ± -->
2
=
sin
вБ° -->
α ќ± -->
1
− вИТ -->
cos
вБ° -->
α ќ± -->
=
1
+
cos
вБ° -->
α ќ± -->
sin
вБ° -->
α ќ± -->
{\displaystyle \operatorname {tg} {\alpha \over 2}={\sin \alpha \over {1+\cos \alpha }}={{1-\cos \alpha } \over \sin \alpha }~,~~~\operatorname {ctg} {\alpha \over 2}={\sin \alpha \over {1-\cos \alpha }}={{1+\cos \alpha } \over \sin \alpha }}
a
sin
вБ° -->
A
+
b
cos
вБ° -->
A
=
r
sin
вБ° -->
(
A
+
B
)
=
r
cos
вБ° -->
(
π ѕА -->
2
− вИТ -->
A
− вИТ -->
B
)
=
a
2
+
b
2
sin
вБ° -->
(
A
+
arctg
вБ° -->
b
a
)
,
r
=
a
2
+
b
2
,
t
g
B
=
b
a
{\displaystyle a\sin A+b\cos A=r\sin {\left(A+B\right)}=r\cos \left({\pi \over 2}-A-B\right)={\sqrt {a^{2}+b^{2}}}\sin {\left(A+\operatorname {arctg} {b \over a}\right)},~{r={\sqrt {a^{2}+b^{2}}}},~{tgB={b \over a}}}
sin
вБ° -->
A
± ¬± -->
sin
вБ° -->
B
=
2
sin
вБ° -->
A
± ¬± -->
B
2
cos
вБ° -->
A
∓ вИУ -->
B
2
{\displaystyle \sin A\pm \sin B=2\sin {{A\pm B} \over 2}\cos {{A\mp B} \over 2}}
cos
вБ° -->
A
+
cos
вБ° -->
B
=
2
cos
вБ° -->
A
+
B
2
cos
вБ° -->
A
− вИТ -->
B
2
{\displaystyle \cos A+\cos B=2\cos {{A+B} \over 2}\cos {{A-B} \over 2}}
cos
вБ° -->
A
− вИТ -->
cos
вБ° -->
B
=
− вИТ -->
2
sin
вБ° -->
A
+
B
2
sin
вБ° -->
A
− вИТ -->
B
2
{\displaystyle \cos A-\cos B=-2\sin {{A+B} \over 2}\sin {{A-B} \over 2}}
tg
вБ° -->
A
± ¬± -->
tg
вБ° -->
B
=
sin
вБ° -->
A
± ¬± -->
B
cos
вБ° -->
A
cos
вБ° -->
B
,
ctg
вБ° -->
A
± ¬± -->
ctg
вБ° -->
B
=
sin
вБ° -->
B
± ¬± -->
A
sin
вБ° -->
A
sin
вБ° -->
B
{\displaystyle \operatorname {tg} A\pm \operatorname {tg} B={\sin {A\pm B} \over {\cos A\cos B}}~,~~\operatorname {ctg} A\pm \operatorname {ctg} B={\sin {B\pm A} \over {\sin A\sin B}}}
–§–Њ—А–Љ—Г–ї–∞ –і–ї—П —Б—Г–Љ–Є –±—Г–і—М-—П–Ї–Њ—Ч –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц —Б–Є–љ—Г—Б—Ц–≤ –Ї—Г—В—Ц–≤ —Ц–Ј —Ч—Е –Ј—Б—Г–≤–Њ–Љ —Ц –Њ—В—А–Є–Љ–∞–љ–љ—П –Њ–і–љ—Ц—Ф—Ч —Д—Г–љ–Ї—Ж—Ц—Ч –Ї—Г—В–∞:
A
sin
вБ° -->
(
x
+
α ќ± -->
)
+
B
sin
вБ° -->
(
x
+
β ќ≤ -->
)
+
C
sin
вБ° -->
(
x
+
γ ќ≥ -->
)
+
.
.
.
=
Y
sin
вБ° -->
x
+
Z
cos
вБ° -->
x
=
Y
2
+
Z
2
sin
вБ° -->
(
x
+
arctg
вБ° -->
Z
Y
)
,
Y
=
A
cos
вБ° -->
(
α ќ± -->
)
+
B
cos
вБ° -->
(
β ќ≤ -->
)
+
C
cos
вБ° -->
(
γ ќ≥ -->
)
+
.
.
.
,
Z
=
A
sin
вБ° -->
(
α ќ± -->
)
+
B
sin
вБ° -->
(
β ќ≤ -->
)
+
C
sin
вБ° -->
(
γ ќ≥ -->
)
+
.
.
.
{\displaystyle A\sin(x+\alpha )+B\sin(x+\beta )+C\sin(x+\gamma )+...=Y\sin x+Z\cos x={\sqrt {Y^{2}+Z^{2}}}\sin(x+\operatorname {arctg} {Z \over Y}),~{Y=A\cos(\alpha )+B\cos(\beta )+C\cos(\gamma )+...},~{Z=A\sin(\alpha )+B\sin(\beta )+C\sin(\gamma )+...}}
–ѓ–Ї—Й–Њ
n
{\displaystyle n}
sin
вБ° -->
n
A
=
(
n
1
)
cos
n
− вИТ -->
1
вБ° -->
A
sin
вБ° -->
A
− вИТ -->
(
n
3
)
cos
n
− вИТ -->
3
вБ° -->
A
sin
3
вБ° -->
A
+
(
n
5
)
cos
n
− вИТ -->
5
вБ° -->
A
sin
5
вБ° -->
A
∓ вИУ -->
⋯ вЛѓ -->
{\displaystyle \sin {nA}={n \choose 1}\cos ^{n-1}A\sin A-{n \choose 3}\cos ^{n-3}A\sin ^{3}A+{n \choose 5}\cos ^{n-5}A\sin ^{5}A\mp \cdots }
cos
вБ° -->
n
A
=
cos
n
вБ° -->
A
− вИТ -->
(
n
2
)
cos
n
− вИТ -->
2
вБ° -->
A
sin
2
вБ° -->
A
+
(
n
4
)
cos
n
− вИТ -->
4
вБ° -->
A
sin
4
вБ° -->
A
∓ вИУ -->
⋯ вЛѓ -->
{\displaystyle \cos {nA}=\cos ^{n}A-{n \choose 2}\cos ^{n-2}A\sin ^{2}A+{n \choose 4}\cos ^{n-4}A\sin ^{4}A\mp \cdots }
–ѓ–Ї—Й–Њ n —Ф —Ж—Ц–ї–Є–Љ –љ–µ–њ–∞—А–љ–Є–Љ —З–Є—Б–ї–Њ–Љ, —В–Њ
sin
n
вБ° -->
x
=
(
− вИТ -->
1
)
n
− вИТ -->
1
2
2
n
− вИТ -->
1
[
sin
вБ° -->
n
x
− вИТ -->
(
n
1
)
sin
вБ° -->
(
n
− вИТ -->
2
)
x
+
(
n
2
)
sin
вБ° -->
(
n
− вИТ -->
4
)
x
− вИТ -->
(
n
3
)
sin
вБ° -->
(
n
− вИТ -->
6
)
x
+
⋯ вЛѓ -->
+
(
− вИТ -->
1
)
n
− вИТ -->
1
2
(
n
n
− вИТ -->
1
2
)
sin
вБ° -->
x
]
{\displaystyle \sin ^{n}x={{(-1)^{{n-1} \over 2}} \over {2^{n-1}}}\left[\sin {nx}-{n \choose 1}\sin {(n-2)x}+{n \choose 2}\sin {(n-4)x}-{n \choose 3}\sin {(n-6)x}+\cdots +(-1)^{{n-1} \over 2}{n \choose {{n-1} \over 2}}\sin x\right]}
cos
n
вБ° -->
x
=
(
1
2
)
n
− вИТ -->
1
[
cos
вБ° -->
n
x
+
(
n
1
)
cos
вБ° -->
(
n
− вИТ -->
2
)
x
+
(
n
2
)
cos
вБ° -->
(
n
− вИТ -->
4
)
x
+
(
n
3
)
cos
вБ° -->
(
n
− вИТ -->
6
)
x
+
⋯ вЛѓ -->
+
(
n
n
− вИТ -->
1
2
)
cos
вБ° -->
x
]
{\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-1} \over 2}}\cos x\right]}
–ѓ–Ї—Й–Њ n —Ф —Ж—Ц–ї–Є–Љ –њ–∞—А–љ–Є–Љ —З–Є—Б–ї–Њ–Љ, —В–Њ
sin
n
вБ° -->
x
=
(
− вИТ -->
1
)
n
2
2
n
− вИТ -->
1
[
cos
вБ° -->
n
x
− вИТ -->
(
n
1
)
cos
вБ° -->
(
n
− вИТ -->
2
)
x
+
(
n
2
)
cos
вБ° -->
(
n
− вИТ -->
4
)
x
− вИТ -->
(
n
3
)
cos
вБ° -->
(
n
− вИТ -->
6
)
x
+
⋯ вЛѓ -->
+
(
− вИТ -->
1
)
n
− вИТ -->
2
2
(
n
n
− вИТ -->
2
2
)
cos
вБ° -->
2
x
]
+
1
2
n
(
n
n
2
)
{\displaystyle \sin ^{n}x={{{\left(-1\right)}^{n \over 2}} \over {2^{n-1}}}\left[\cos {nx}-{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}-{n \choose 3}\cos {(n-6)x}+\cdots +{\left(-1\right)}^{{n-2} \over 2}{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}
cos
n
вБ° -->
x
=
(
1
2
)
n
− вИТ -->
1
[
cos
вБ° -->
n
x
+
(
n
1
)
cos
вБ° -->
(
n
− вИТ -->
2
)
x
+
(
n
2
)
cos
вБ° -->
(
n
− вИТ -->
4
)
x
+
(
n
3
)
cos
вБ° -->
(
n
− вИТ -->
6
)
x
+
⋯ вЛѓ -->
+
(
n
n
− вИТ -->
2
2
)
cos
вБ° -->
2
x
]
+
1
2
n
(
n
n
2
)
{\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}
–Ж—Б–љ—Г—О—В—М —В–∞–Ї—Ц —А–Њ–Ј–Ї–ї–∞–і–Є –≤ —А—П–і –Ґ–µ–є–ї–Њ—А–∞ —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є:
sin
вБ° -->
x
=
x
− вИТ -->
x
3
3
!
+
x
5
5
!
− вИТ -->
x
7
7
!
+
⋯ вЛѓ -->
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
cos
вБ° -->
x
=
1
− вИТ -->
x
2
2
!
+
x
4
4
!
− вИТ -->
x
6
6
!
+
⋯ вЛѓ -->
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
x
2
n
(
2
n
)
!
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
tg
вБ° -->
x
=
∑ вИС -->
n
=
0
∞ вИЮ -->
U
2
n
+
1
x
2
n
+
1
(
2
n
+
1
)
!
=
∑ вИС -->
n
=
1
∞ вИЮ -->
(
− вИТ -->
1
)
n
− вИТ -->
1
2
2
n
(
2
2
n
− вИТ -->
1
)
B
2
n
x
2
n
− вИТ -->
1
(
2
n
)
!
=
x
+
x
3
3
+
2
x
5
15
+
17
x
7
315
+
62
x
9
2835
+
⋯ вЛѓ -->
,
при
|
x
|
<
π ѕА -->
2
{\displaystyle {\begin{aligned}\operatorname {tg} x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\\&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+{\frac {62x^{9}}{2835}}+\cdots ,\qquad {\text{–њ—А–Є }}|x|<{\frac {\pi }{2}}\end{aligned}}}
–і–µ
U
n
{\displaystyle U_{n}}
n -—В–µ –њ–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –С—Г—Б—В—А–Њ—Д–µ–і–Њ–љ–∞ ,
B
n
{\displaystyle B_{n}}
—З–Є—Б–ї–∞ –С–µ—А–љ—Г–ї–ї—Ц , —В–∞
E
n
{\displaystyle E_{n}}
—З–Є—Б–ї–∞ –Х–є–ї–µ—А–∞ .
cosec
вБ° -->
x
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
+
1
2
(
2
2
n
− вИТ -->
1
− вИТ -->
1
)
B
2
n
x
2
n
− вИТ -->
1
(
2
n
)
!
=
1
x
+
x
6
+
7
x
3
360
+
31
x
5
15120
+
⋯ вЛѓ -->
,
при
0
<
|
x
|
<
π ѕА -->
{\displaystyle {\begin{aligned}\operatorname {cosec} x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}={\frac {1}{x}}+{\frac {x}{6}}+{\frac {7x^{3}}{360}}+{\frac {31x^{5}}{15120}}+\cdots ,\qquad {\text{–њ—А–Є }}0<|x|<\pi \end{aligned}}}
sec
вБ° -->
x
=
∑ вИС -->
n
=
0
∞ вИЮ -->
U
2
n
x
2
n
(
2
n
)
!
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
E
2
n
x
2
n
(
2
n
)
!
=
1
+
x
2
2
+
5
x
4
24
+
61
x
6
720
+
⋯ вЛѓ -->
,
при
|
x
|
<
π ѕА -->
2
{\displaystyle {\begin{aligned}\sec x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\\&{}=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+{\frac {61x^{6}}{720}}+\cdots ,\qquad {\text{–њ—А–Є }}|x|<{\frac {\pi }{2}}\end{aligned}}}
ctg
вБ° -->
x
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
2
2
n
B
2
n
x
2
n
− вИТ -->
1
(
2
n
)
!
=
1
x
− вИТ -->
x
3
− вИТ -->
x
3
45
− вИТ -->
2
x
5
945
− вИТ -->
⋯ вЛѓ -->
,
при
0
<
|
x
|
<
π ѕА -->
{\displaystyle {\begin{aligned}\operatorname {ctg} x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\\&{}={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-\cdots ,\qquad {\text{–њ—А–Є }}0<|x|<\pi \end{aligned}}}
–Т–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—З–Є –≤–Є—Й–µ–љ–∞–≤–µ–і–µ–љ—Ц —А–Њ–Ј–Ї–ї–∞–і–Є –≤ —А—П–і–Є –Ґ–µ–є–ї–Њ—А–∞ –Љ–Њ–ґ–љ–∞ –њ–Њ–Ї–∞–Ј–∞—В–Є, —Й–Њ —Д—Г–љ–Ї—Ж—Ц—Ч
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
e
i
θ ќЄ -->
=
cos
вБ° -->
θ ќЄ -->
+
i
sin
вБ° -->
θ ќЄ -->
.
{\displaystyle e^{i\theta }=\cos \theta +i\sin \theta .\,}
–¶–µ —Б–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —Д–Њ—А–Љ—Г–ї–Њ—О –Х–є–ї–µ—А–∞ .
–Ь–Њ–ґ–љ–∞ –≤–Є–Ј–љ–∞—З–Є—В–Є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ—Ч –Ј–Љ—Ц–љ–љ–Њ—Ч z :
sin
вБ° -->
z
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
=
e
i
z
− вИТ -->
e
− вИТ -->
i
z
2
i
=
− вИТ -->
i
sh
вБ° -->
(
i
z
)
,
{\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\,=\,{e^{iz}-e^{-iz} \over 2i}=-i\operatorname {sh} \left(iz\right),}
cos
вБ° -->
z
=
∑ вИС -->
n
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
n
(
2
n
)
!
z
2
n
=
e
i
z
+
e
− вИТ -->
i
z
2
=
ch
вБ° -->
(
i
z
)
{\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\,=\,{e^{iz}+e^{-iz} \over 2}=\operatorname {ch} \left(iz\right)}
–і–µ
i
2
=
− вИТ -->
1
{\displaystyle i^{2}=-1}
sh
вБ° -->
x
{\displaystyle \operatorname {sh} x}
ch
вБ° -->
x
{\displaystyle \operatorname {ch} x}
–≥—Ц–њ–µ—А–±–Њ–ї—Ц—З–љ—Ц —Б–Є–љ—Г—Б —В–∞ –Ї–Њ—Б–Є–љ—Г—Б. –Ф–ї—П –і—Ц–є—Б–љ–Њ–≥–Њ
x
{\displaystyle x}
cos
вБ° -->
x
=
Re
вБ° -->
(
e
i
x
)
,
sin
вБ° -->
x
=
Im
вБ° -->
(
e
i
x
)
{\displaystyle \cos x=\operatorname {Re} (e^{ix})~,~~~~\sin x=\operatorname {Im} (e^{ix})}
–Ъ–Њ–Љ–њ–ї–µ–Ї—Б–љ–Є–є —Б–Є–љ—Г—Б –Ъ–Њ–Љ–њ–ї–µ–Ї—Б–љ–Є–є –Ї–Њ—Б–Є–љ—Г—Б –Ъ–Њ–Љ–њ–ї–µ–Ї—Б–љ–Є–є —В–∞–љ–≥–µ–љ—Б
f
(
x
)
{\displaystyle \ \ \ \ f(x)}
d
d
x
f
(
x
)
{\displaystyle {\frac {d}{dx}}f(x)}
∫ вИЂ -->
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx}
sin
вБ° -->
x
{\displaystyle \,\ \sin x}
cos
вБ° -->
x
{\displaystyle \,\ \cos x}
− вИТ -->
cos
вБ° -->
x
+
C
{\displaystyle \,\ -\cos x+C}
cos
вБ° -->
x
{\displaystyle \,\ \cos x}
− вИТ -->
sin
вБ° -->
x
{\displaystyle \,\ -\sin x}
sin
вБ° -->
x
+
C
{\displaystyle \,\ \sin x+C}
tg
вБ° -->
x
{\displaystyle \,\ \operatorname {tg} x}
sec
2
вБ° -->
x
{\displaystyle \,\ \sec ^{2}x}
− вИТ -->
ln
вБ° -->
|
cos
вБ° -->
x
|
+
C
{\displaystyle -\ln \left|\cos x\right|+C}
ctg
вБ° -->
x
{\displaystyle \,\ \operatorname {ctg} x}
− вИТ -->
cosec
2
вБ° -->
x
{\displaystyle \,\ -\operatorname {cosec} ^{2}x}
ln
вБ° -->
|
sin
вБ° -->
x
|
+
C
{\displaystyle \ln \left|\sin x\right|+C}
sec
вБ° -->
x
{\displaystyle \,\ \sec x}
sec
вБ° -->
x
tg
вБ° -->
x
{\displaystyle \,\ \sec {x}\operatorname {tg} {x}}
ln
вБ° -->
|
sec
вБ° -->
x
+
tg
вБ° -->
x
|
+
C
{\displaystyle \ln \left|\sec x+\operatorname {tg} x\right|+C}
cosec
вБ° -->
x
{\displaystyle \,\ \operatorname {cosec} x}
− вИТ -->
cosec
вБ° -->
x
ctg
вБ° -->
x
{\displaystyle \,\ -\operatorname {cosec} {x}\operatorname {ctg} {x}}
− вИТ -->
ln
вБ° -->
|
cosec
вБ° -->
x
+
ctg
вБ° -->
x
|
+
C
{\displaystyle -\ln \left|\operatorname {cosec} x+\operatorname {ctg} x\right|+C}
–§—Г–љ–Ї—Ж—Ц—Ч
sin
x
{\displaystyle \sin \,x}
cos
x
{\displaystyle \cos \,x}
–і–Є—Д–µ—А–µ–љ—Ж—Ц–∞–ї—М–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П –≥–∞—А–Љ–Њ–љ—Ц—З–љ–Є—Е –Ї–Њ–ї–Є–≤–∞–љ—М
d
2
y
d
x
2
+
y
=
0
{\displaystyle {d^{2}y \over d{x^{2}}}+y=0}
–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
sin
вБ° -->
A
a
=
sin
вБ° -->
B
b
=
sin
вБ° -->
C
c
=
2
Δ ќФ -->
a
b
c
,
{\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}={\frac {2\Delta }{abc}},}
–і–µ
Δ ќФ -->
{\displaystyle \Delta }
a
sin
вБ° -->
A
=
b
sin
вБ° -->
B
=
c
sin
вБ° -->
C
=
2
R
,
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R,}
–і–µ
R
{\displaystyle R}
–Ї–Њ–ї–∞, —Й–Њ –Њ–њ–Є—Б—Г—Ф —В—А–Є–Ї—Г—В–љ–Є–Ї .
–§—Ц–≥—Г—А–∞ –Ы—Ц—Б—Б–∞–ґ—Г , —Д—Ц–≥—Г—А–∞ —Г—В–≤–Њ—А–µ–љ–∞ –љ–∞ –Њ—Б–љ–Њ–≤—Ц —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ–Њ—Ч —Д—Г–љ–Ї—Ж—Ц—Ч.–¶–µ –Љ–Њ–ґ–љ–∞ –і–Њ–≤–µ—Б—В–Є —А–Њ–Ј–і—Ц–ї–Є–≤—И–Є —В—А–Є–Ї—Г—В–љ–Є–Ї –љ–∞ –і–≤–∞ –њ—А—П–Љ–Њ–Ї—Г—В–љ–Є—Е —В—А–Є–Ї—Г—В–љ–Є–Ї–Є, —Ц –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—З–Є –≤–Є–Ј–љ–∞—З–µ–љ–љ—П —Б–Є–љ—Г—Б–∞. –Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ –Ї–Њ—А–Є—Б–љ–∞ –і–ї—П —А–Њ–Ј—А–∞—Е—Г–љ–Ї—Г –і–Њ–≤–ґ–Є–љ –љ–µ–≤—Ц–і–Њ–Љ–Є—Е —Б—В–Њ—А—Ц–љ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, –њ—А–Є –≤—Ц–і–Њ–Љ–Є—Е –і–≤–Њ—Е –Ї—Г—В–∞—Е —Ц –і–Њ–≤–ґ–Є–љ—Ц –Њ–і–љ—Ц—Ф—Ч –Ј –є–Њ–≥–Њ —Б—В–Њ—А—Ц–љ. –¶—П —Б–Є—В—Г–∞—Ж—Ц—П —Ф —В–Є–њ–Њ–≤–Њ—О –і–ї—П –Ј–∞–і–∞—З—Ц —В—А–Є–∞–љ–≥—Г–ї—П—Ж—Ц—Ч
–Ґ–µ–Њ—А–µ–Љ–∞ –Ї–Њ—Б–Є–љ—Г—Б—Ц–≤ —В–µ–Њ—А–µ–Љ–Є –Я—Ц—Д–∞–≥–Њ—А–∞ :
c
2
=
a
2
+
b
2
− вИТ -->
2
a
b
cos
вБ° -->
C
,
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C,\,}
–∞–±–Њ –µ–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–Њ,
cos
вБ° -->
C
=
a
2
+
b
2
− вИТ -->
c
2
2
a
b
.
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.}
–Т —Ж—Ц–є —Д–Њ—А–Љ—Г–ї—Ц –Ї—Г—В
C
{\displaystyle C}
c
{\displaystyle c}
–Ґ–µ–Њ—А–µ–Љ—Г –Ї–Њ—Б–Є–љ—Г—Б—Ц–≤ –Љ–Њ–ґ–љ–∞ –Ј–∞—Б—В–Њ—Б—Г–≤–∞—В–Є –і–ї—П –≤–Є–Ј–љ–∞—З–µ–љ–љ—П —Б—В–Њ—А–Њ–љ–Є —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, —П–Ї—Й–Њ –≤—Ц–і–Њ–Љ—Ц –і–Њ–≤–ґ–Є–љ–Є –і–≤–Њ—Е —Б—В–Њ—А—Ц–љ —Ц –Ї—Г—В –Љ—Ц–ґ –љ–Є–Љ–Є. –Ґ–∞–Ї–Њ–ґ —Ч—Ч –Љ–Њ–ґ–љ–∞ –Ј–∞—Б—В–Њ—Б—Г–≤–∞—В–Є –і–ї—П –≤–Є–Ј–љ–∞—З–µ–љ–љ—П –Ї–Њ—Б–Є–љ—Г—Б–∞ –Ї—Г—В–∞ (—Ц –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ –Ј–љ–∞—З–µ–љ–љ—П —Б–∞–Љ–Њ–≥–Њ –Ї—Г—В–∞) —П–Ї—Й–Њ –≤—Ц–і–Њ–Љ—Ц –і–Њ–≤–ґ–Є–љ–Є –≤—Б—Ц—Е —Б—В–Њ—А—Ц–љ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞.
–Т—Б—Ц –љ–∞—Б—В—Г–њ–љ—Ц –≤–Є—А–∞–Ј–Є —Д–Њ—А–Љ—Г–ї—О—О—В—М —В–µ–Њ—А–µ–Љ—Г —В–∞–љ–≥–µ–љ—Б—Ц–≤[ 1]
tg
вБ° -->
A
− вИТ -->
B
2
tg
вБ° -->
A
+
B
2
=
a
− вИТ -->
b
a
+
b
;
tg
вБ° -->
A
− вИТ -->
C
2
tg
вБ° -->
A
+
C
2
=
a
− вИТ -->
c
a
+
c
;
tg
вБ° -->
B
− вИТ -->
C
2
tg
вБ° -->
B
+
C
2
=
b
− вИТ -->
c
b
+
c
{\displaystyle {\frac {\operatorname {tg} {\dfrac {A-B}{2}}}{\operatorname {tg} {\dfrac {A+B}{2}}}}={\frac {a-b}{a+b}}\,;\qquad {\frac {\operatorname {tg} {\dfrac {A-C}{2}}}{\operatorname {tg} {\dfrac {A+C}{2}}}}={\frac {a-c}{a+c}}\,;\qquad {\frac {\operatorname {tg} {\dfrac {B-C}{2}}}{\operatorname {tg} {\dfrac {B+C}{2}}}}={\frac {b-c}{b+c}}}
–Я–Њ—П—Б–љ–µ–љ–љ—П —Ж–Є—Е —Д–Њ—А–Љ—Г–ї –љ–∞ —Б–ї–Њ–≤–∞—Е –±—Г–ї–Њ –± –≥—А–Њ–Љ—Ц–Ј–і–Ї–Є–Љ, –∞–ї–µ –Ј–∞–Ї–Њ–љ–Њ–Љ—Ц—А–љ–Њ—Б—В—Ц —Б—Г–Љ —Ц —А—Ц–Ј–љ–Є—Ж—М –і–ї—П –і–Њ–≤–ґ–Є–љ —Б—В–Њ—А—Ц–љ —Ц –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Є—Е –њ—А–Њ—В–Є–ї–µ–ґ–љ–Є—Е –Ї—Г—В—Ц–≤ –≤–Є–і–љ–Њ —Ц–Ј —В–µ–Њ—А–µ–Љ–Є.
–ѓ–Ї—Й–Њ
ζ ќґ -->
=
1
s
(
s
− вИТ -->
a
)
(
s
− вИТ -->
b
)
(
s
− вИТ -->
c
)
{\displaystyle \zeta ={\sqrt {{\frac {1}{s}}(s-a)(s-b)(s-c)}}\ }
—Ц
s
=
a
+
b
+
c
2
{\displaystyle s={\frac {a+b+c}{2}}\ }
—В–Њ–і—Ц –≤—Б—Ц –љ–∞—Б—В—Г–њ–љ—Ц —Д–Њ—А–Љ—Г–ї–Є –Њ–њ–Є—Б—Г—О—В—М —В–µ–Њ—А–µ–Љ—Г –Ї–Њ—В–∞–љ–≥–µ–љ—Б—Ц–≤[ 1]
ctg
вБ° -->
A
2
=
s
− вИТ -->
a
ζ ќґ -->
;
ctg
вБ° -->
B
2
=
s
− вИТ -->
b
ζ ќґ -->
;
ctg
вБ° -->
C
2
=
s
− вИТ -->
c
ζ ќґ -->
{\displaystyle \operatorname {ctg} {\frac {A}{2}}={\frac {s-a}{\zeta }}\,;\qquad \operatorname {ctg} {\frac {B}{2}}={\frac {s-b}{\zeta }}\,;\qquad \operatorname {ctg} {\frac {C}{2}}={\frac {s-c}{\zeta }}}
–Ч–≤—Ц–і—Б–Є –≤–Є–њ–ї–Є–≤–∞—Ф, —Й–Њ
ctg
вБ° -->
A
2
s
− вИТ -->
a
=
ctg
вБ° -->
B
2
s
− вИТ -->
b
=
ctg
вБ° -->
C
2
s
− вИТ -->
c
.
{\displaystyle {\frac {\operatorname {ctg} {\dfrac {A}{2}}}{s-a}}={\frac {\operatorname {ctg} {\dfrac {B}{2}}}{s-b}}={\frac {\operatorname {ctg} {\dfrac {C}{2}}}{s-c}}.}
–Э–∞ —Б–ї–Њ–≤–∞—Е —В–µ–Њ—А–µ–Љ–∞ –њ–Њ–ї—П–≥–∞—Ф –≤ —В–Њ–Љ—Г, —Й–Њ –Ї–Њ—В–∞–љ–≥–µ–љ—Б –њ–Њ–ї–Њ–≤–Є–љ–љ–Њ–≥–Њ –Ї—Г—В–∞ –і–Њ—А—Ц–≤–љ—О—Ф –≤—Ц–і–љ–Њ—И–µ–љ–љ—О –љ–∞–њ—Ц–≤–њ–µ—А–Є–Љ–µ—В—А–∞ –≤—Ц–і —П–Ї–Њ–≥–Њ –≤—Ц–і–љ—П—В–Њ —Б—В–Њ—А–Њ–љ—Г –њ—А–Њ—В–Є–ї–µ–ґ–љ—Г –Ј–∞–і–∞–љ–Њ–Љ—Г –Ї—Г—В—Г, –і–Њ —А–∞–і—Ц—Г—Б–∞ –≤–њ–Є—Б–∞–љ–Њ–≥–Њ –Ї–Њ–ї–∞.
–Р–љ—Ц–Љ–∞—Ж—Ц—П –∞–і–Є—В–Є–≤–љ–Њ–≥–Њ —Б–Є–љ—В–µ–Ј—Г [en] –Љ–µ–∞–љ–і—А—Г —Ц–Ј –Ј–±—Ц–ї—М—И–µ–љ–љ—П–Љ –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –≥–∞—А–Љ–Њ–љ—Ц–Ї –°–Є–љ—Г—Б–Њ—Ч–і–∞–ї—М–љ—Ц –±–∞–Ј–Є—Б–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч (–Ј–љ–Є–Ј—Г) –Љ–Њ–ґ—Г—В—М —Б—Д–Њ—А–Љ—Г–≤–∞—В–Є –њ–Є–ї–Њ–њ–Њ–і—Ц–±–љ—Г —Е–≤–Є–ї—О (–Ј–≤–µ—А—Е—Г), —П–Ї—Й–Њ —Ч—Е –і–Њ–і–∞—В–Є –Љ—Ц–ґ —Б–Њ–±–Њ—О. –Т—Б—Ц –±–∞–Ј–Њ–≤—Ц —Д—Г–љ–Ї—Ж—Ц—Ч –Љ–∞—В–Є–Љ—Г—В—М –≤—Г–Ј–ї–Є, —Й–Њ –Ј–±—Ц–≥–∞—О—В—М—Б—П –Ј –≤—Г–Ј–ї–∞–Љ–Є –њ–Є–ї–Њ–њ–Њ–і—Ц–±–љ–Њ—Ч —Е–≤–Є–ї—Ц, —Ц –≤—Б—Ц –Ї—А—Ц–Љ –Њ—Б–љ–Њ–≤–љ–Њ—Ч (
k
=
1
{\displaystyle k=1}
k –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П —П–≤–Є—Й–µ–Љ –У—Ц–±–±—Б–∞ [en] –Ґ—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч —В–∞–Ї–Њ–ґ –Љ–∞—О—В—М –≤–∞–ґ–ї–Є–≤–µ –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Г —Д—Ц–Ј–Є—Ж—Ц. –§—Г–љ–Ї—Ж—Ц—Ч —Б–Є–љ—Г—Б–∞ —Ц –Ї–Њ—Б–Є–љ—Г—Б–∞, –љ–∞–њ—А–Є–Ї–ї–∞–і, –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—В—М –і–ї—П –Њ–њ–Є—Б–∞–љ–љ—П –≥–∞—А–Љ–Њ–љ—Ц—З–љ–Є—Е –Ї–Њ–ї–Є–≤–∞–љ—М , —П–Ї—Ц –Љ–Њ–і–µ–ї—О—О—В—М –±–∞–≥–∞—В–Њ –њ—А–Є—А–Њ–і–љ–Є—Е —П–≤–Є—Й, —В–∞–Ї—Ц —П–Ї —А—Г—Е –Љ–∞—Б–Є –Ј–∞–Ї—А—Ц–њ–ї–µ–љ–Њ—Ч –љ–∞ –њ—А—Г–ґ–Є–љ—Ц, —Ц –і–ї—П –Љ–∞–ї–Є—Е –Ї—Г—В—Ц–≤, —А—Г—Е –Љ–∞—П—В–љ–Є–Ї–∞ –і–ї—П –Љ–∞—Б–Є —Й–Њ –≤–Є—Б–Є—В—М –љ–∞ –љ–Є—В—Ж—Ц. –§—Г–љ–Ї—Ж—Ц—Ч —Б–Є–љ—Г—Б–∞ —Ц –Ї–Њ—Б–Є–љ—Г—Б–∞ —Ф –Њ–і–љ–Њ–≤–Є–Љ—Ц—А–љ–Є–Љ–Є –њ—А–Њ—Ф–Ї—Ж—Ц—П–Љ–Є —А—Ц–≤–љ–Њ–Љ—Ц—А–љ–Њ–≥–Њ –Ї—А—Г–≥–Њ–≤–Њ–≥–Њ —А—Г—Е—Г .
–Ґ—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч —В–∞–Ї–Њ–ґ –і–Њ–≤–µ–ї–Є —Б–≤–Њ—О –Ї–Њ—А–Є—Б—В—М –њ—А–Є –≤–Є–≤—З–µ–љ–љ—Ц –Ј–∞–≥–∞–ї—М–љ–Є—Е –њ–µ—А—Ц–Њ–і–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є . –•–∞—А–∞–Ї—В–µ—А–љ–∞ —Е–≤–Є–ї—М–Њ–≤–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –њ–µ—А—Ц–Њ–і–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є –Ї–Њ—А–Є—Б–љ–∞ –і–ї—П –Љ–Њ–і–µ–ї—О–≤–∞–љ–љ—П —П–≤–Є—Й, —В–∞–Ї–Є—Е —П–Ї –Ј–≤—Г–Ї–Њ–≤—Ц –∞–±–Њ —Б–≤—Ц—В–ї–Њ–≤—Ц —Е–≤–Є–ї—Ц .[ 2]
–Т –Ј–∞–≥–∞–ї—М–љ–Є—Е —Г–Љ–Њ–≤–∞—Е, –њ–µ—А—Ц–Њ–і–Є—З–љ—Г —Д—Г–љ–Ї—Ж—Ц—О
f
(
x
)
{\displaystyle f(x)}
–†—П–і—Г –§—Г—А'—Ф .[ 3] –±–∞–Ј–Є—Б–љ—Ц —Д—Г–љ–Ї—Ж—Ц—Ч —П–Ї
φ ѕЖ -->
k
{\displaystyle \varphi _{k}}
f
(
x
)
{\displaystyle f(x)}
f
(
t
)
=
∑ вИС -->
k
=
1
∞ вИЮ -->
c
k
φ ѕЖ -->
k
(
t
)
.
{\displaystyle f(t)=\sum _{k=1}^{\infty }c_{k}\varphi _{k}(t).}
–Э–∞–њ—А–Є–Ї–ї–∞–і, –Ї–≤–∞–і—А–∞—В–љ—Г —Е–≤–Є–ї—О (–Љ–µ–∞–љ–і—А) –Љ–Њ–ґ–љ–∞ –Ј–∞–њ–Є—Б–∞—В–Є —Г –≤–Є–≥–ї—П–і—Ц —А—П–і—Г –§—Г—А'—Ф
f
square
(
t
)
=
4
π ѕА -->
∑ вИС -->
k
=
1
∞ вИЮ -->
sin
вБ° -->
(
(
2
k
− вИТ -->
1
)
t
)
2
k
− вИТ -->
1
.
{\displaystyle f_{\text{square}}(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\big (}(2k-1)t{\big )} \over 2k-1}.}
–Т –∞–љ—Ц–Љ–∞—Ж—Ц—Ч –Ї–≤–∞–і—А–∞—В–љ–Њ—Ч —Е–≤–Є–ї—Ц –њ—А–∞–≤–Њ—А—Г—З –Љ–Њ–ґ–љ–∞ –њ–Њ–±–∞—З–Є—В–Є, —Й–Њ –ї–Є—И–µ –і–µ–Ї—Ц–ї—М–Ї–∞ —В–µ—А–Љ—Ц–≤ –≤–ґ–µ –і–Њ—Б–Є—В—М –∞–±–Є —Б—В–≤–Њ—А–Є—В–Є –і–Њ–±—А—Г –∞–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж—Ц—О –Ї–≤–∞–і—А–∞—В–љ–Њ—Ч —Д–Њ—А–Љ–Є —Е–≤–Є–ї—Ц. –°—Г–њ–µ—А–њ–Њ–Ј–Є—Ж—Ц—О –і–µ–Ї—Ц–ї—М–Ї–Њ—Е —В–µ—А–Љ—Ц–≤ –≤ —А–Њ–Ј–Ї–ї–∞–і–∞–љ–љ—Ц –њ–Є–ї–Њ–њ–Њ–і—Ц–±–љ–Њ—Ч —Е–≤–Є–ї—Ц –Љ–Њ–ґ–љ–∞ –њ–Њ–±–∞—З–Є—В–Є –Ј–љ–Є–Ј—Г –њ—Ц–і —В–Є–Љ –Љ–∞–ї—О–љ–Ї–Њ–Љ.







































![{\displaystyle \left[0,{\pi \over 2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab3e12a574b4dbd6b987141068819ab87c3ef1a7)

























![{\displaystyle \sin ^{n}x={{(-1)^{{n-1} \over 2}} \over {2^{n-1}}}\left[\sin {nx}-{n \choose 1}\sin {(n-2)x}+{n \choose 2}\sin {(n-4)x}-{n \choose 3}\sin {(n-6)x}+\cdots +(-1)^{{n-1} \over 2}{n \choose {{n-1} \over 2}}\sin x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9c9d332aa56967b8aa170857a73ec20e386a829)
![{\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-1} \over 2}}\cos x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bb64d03b323cc4db9eac951d5b889d37c53432c)
![{\displaystyle \sin ^{n}x={{{\left(-1\right)}^{n \over 2}} \over {2^{n-1}}}\left[\cos {nx}-{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}-{n \choose 3}\cos {(n-6)x}+\cdots +{\left(-1\right)}^{{n-2} \over 2}{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d813f40bb6eb86943aa2d3f077c55e4b91c4d7f0)
![{\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9212084773b0d9e587274d75ca94f070bc8acb58)






































































