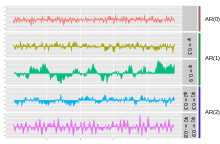
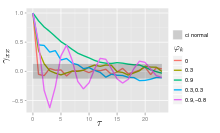
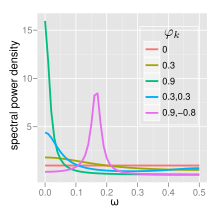
Авторегресійна модель
|
Read other articles:

スタンリー・マシューズ ストーク・シティでのマシューズ (1962年)名前愛称 ドリブルの魔術師ラテン文字 Stanley MATTHEWS基本情報国籍 イングランド生年月日 (1915-02-01) 1915年2月1日出身地 ハンリー没年月日 (2000-02-23) 2000年2月23日(85歳没)身長 174cm体重 71kg選手情報ポジション FW / MF (RWG, RSH)利き足 右足ユース1930-1932 ストーク・シティクラブ1年 クラブ 出場 (得点)1932-1947 スト...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2021) ضريبة الرعاية الصحية والاجتماعية هي ضريبة مقترحة في المملكة المتحدة يتم تحصيلها من قبل حكومة المملكة المتحدة للإنفاق الإضافي على الصحة، والمتوقع أن يتم إطل

Edith Soterius von Sachsenheim Información personalNacimiento 26 de diciembre de 1887 Feldioara (Rumania) Fallecimiento 4 de enero de 1970 (82 años)Londres (Reino Unido) Nacionalidad RumanaEducaciónEducada en Academia de Bellas Artes de Múnich Información profesionalOcupación Pintora Género Retrato [editar datos en Wikidata] Edith Jeanette Soterius von Sachsenheim (Feldioara, 26 de diciembre de 1887 – Londres, 4 de enero de 1970) fue una pintora sajona de Transilvania, que ...

Sekolah Tinggi Ilmu Ekonomi Budi Utomo ManadoJenisBadan Hukum Milik YayasanDidirikan1976 (Izin Oprasional 1982)RektorRosalie Anneke Jacob, S.Pd., SE.AlamatJl. 14 Februari Teling Atas, Kecamatan Wanea, Manado, Manado, Sulawesi Utara, IndonesiaNama julukanSTIE-BU Manado Sekolah Tinggi Ilmu Ekonomi (STIE) Budi Utomo Manado adalah sebuah sekolah tinggi swasta yang terletak di Manado, Sulawesi Utara, Indonesia. STIE Budi Utomo Manado adalah sekolah tinggi Ilmu Ekonomi berbadan hukum Yayasan Pendid...

Hammershøj Parochie van Denemarken Situering Bisdom Bisdom Viborg Gemeente Viborg Coördinaten 56°30'2,999NB, 9°45'19,001OL Algemeen Inwoners (2004) 972 Leden Volkskerk (2004) 893 Overig Kerken Hammershøj Kirke Proosdij Viborg Østre Provsti Pastoraat Vorning-Kvorning-Hammershøj Foto's Portaal Denemarken Hammershøj is een parochie van de Deense Volkskerk in de Deense gemeente Viborg. De parochie maakt deel uit van het bisdom Viborg en telt 893 kerkleden op een bevolking van...

Medaillon von Ferdinand Müller an der Kunsthalle Hamburg Ferdinand Müller (* 16. Oktober 1809 in Meiningen; † 6. September 1881 ebenda)[1] war ein deutscher Bildhauer. Inhaltsverzeichnis 1 Leben 2 Werke 3 Literatur 4 Weblinks 5 Einzelnachweise Leben Ferdinand Müller begann seine Ausbildung bei seinem Vater, dem Hofbildhauer Christian Müller. Ab 1830 studierte er an der Akademie der Bildenden Künste München im Atelier von Ludwig Schwanthaler. Von 1840 bis zu seinem Tod war er a...

Eingang zu einer Apotheke in Oldenburg mit Logo, Einhorn und historischen Darstellungen von Apothekern (um 1900) Die Apotheke am Rathaus in Alsfeld wird seit 1683 betrieben Die Mohren-Apotheke in Bayreuth Die Alte Apotheke von 1889 in Bremen-Hemelingen Mobile Apotheke in der Gemeinde Pomßen, Sachsen, 1988 Als Apotheke wird ein Ort bezeichnet, an dem Arzneimittel und Medizinprodukte abgegeben, geprüft und hergestellt werden. Zudem ist es eine Hauptaufgabe des Apothekers und des übrigen Apot...

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve th...

Political Dispute in Pakistan This article needs to be updated. Please help update this article to reflect recent events or newly available information. (April 2023) 2023 Pakistan Election Delay CaseCourtSupreme Court of PakistanCase historyPrior action(s)Election Commission of Pakistan deferred the Punjab and Khyber Pakhtunkhwa elections from 30 April to 8 October 2023Subsequent action(s)Ongoing caseCourt membershipJudges sittingChief Justice of Pakistan Umar Ata Bandial, Justice Ijaz Ul Ahs...

Fantastic FourBerkas:FF509.jpgSeni promosi untuk Fantastic Four #509 (Maret 2004)oleh Mike Wieringo dan Karl KeselInformasi publikasiPenerbitMarvel ComicsPenampilan pertamaThe Fantastic Four #1 (November, 1961)Dibuat olehStan Lee (penulis)Jack Kirby (ilustrasi)Informasi dalam ceritaBasis Baxter Building Avengers Mansion (dahulu) Four Freedoms Plaza Pier 4 Anggota Mister Fantastic Invisible Woman Human Torch The Thing DaftarLihat:Daftar anggota Fantastic Four Fantastic Four adalah sebuah tim p...

Vrhnika Basisdaten Staat Slowenien Slowenien Historische Region Innerkrain/Notranjska Statistische Region Osrednjeslovenska (Zentralslowenien) Koordinaten 45° 58′ N, 14° 18′ O45.96666666666714.2975293Koordinaten: 45° 58′ 0″ N, 14° 17′ 51″ O Höhe 293 m. i. J. Fläche 126,3 km² Einwohner 17.858 (2022) Bevölkerungsdichte 141 Einwohner je km² Postleitzahl 1360 Kfz-Kennzeichen LJ Struktur und Verwaltung ...

1967 film by Michael D. Moore This article is about the 1967 American film. For the 1988 Russian-German film, see To Kill a Dragon. This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (...

Istana Azem yang menggunakan teknik ablaq Ablaq merupakan gaya arsitektur yang melibatkan baris cahaya dan batu gelap bergantian atau berfluktuasi, yang berkaitan dengan dekorasi arsitektur islami Arab. Penggunaan istilah ablaq pertama yang tercatat yaitu pada perbaikan Masjid Agung Damaskus pada tahun 1109, tapi teknik itu sendiri telah digunakan jauh sebelumnya. Teknik ini adalah fitur arsitektur Islam. Teknik dekoratif ablaq sendiri menggunakan susunan dari batu ashlar berwarna terang dan ...

American politician Ben W. Hooper31st Governor of TennesseeIn officeJanuary 26, 1911 – January 17, 1915Preceded byMalcolm R. PattersonSucceeded byThomas Clarke RyeMember of the Tennessee House of RepresentativesIn office1893–1897 Personal detailsBornBennie Walter Wade(1870-10-13)October 13, 1870Newport, Tennessee, USDiedApril 18, 1957(1957-04-18) (aged 86)Carson Springs, TennesseeResting placeUnion Cemetery, Newport, TennesseePolitical partyRepublicanSpouseAnna Belle...

MTV Africa Music Awards 2014Date7 June 2014 (2014-06-07)LocationDurban International Convention Centre, KwaZulu-Natal, South AfricaHosted byMarlon WayansTelevision/radio coverageNetworkMTV, MTV Base ← 2010 · MTV Africa Music Awards · 2015 → The MTV Africa Music Awards 2014 took place on 7 June 2014, at the Durban International Convention Centre (ICC Arena). The awards aired live across Africa on MTV Base and MTV. The ceremony was sponsored by K...

Jaime Rodríguez Calderón Rodríguez Calderón en septiembre de 2015. Gobernador de Nuevo León 2 de julio de 2018-3 de octubre de 2021Predecesor Florentino González FloresSucesor Samuel García Sepúlveda 4 de octubre de 2015-31 de diciembre de 2017Predecesor Rodrigo Medina de la CruzSucesor Florentino González Flores Presidente municipal de García 1 de noviembre de 2009-31 de octubre de 2012Predecesor Guadalupe Valadez ArrambideSucesor Jesús Hernández Martínez Diputado del Congreso d...

High jump technique Straddle Technique The straddle technique was the dominant style in the high jump before the development of the Fosbury Flop. It is a successor of the Western roll,[1] with which it is sometimes confused. Unlike the scissors or flop style of jump, where the jumper approaches the bar so as to take off from the outer foot, the straddle jumper approaches from the opposite side, so as to take off from the inner foot. In this respect the straddle resembles the western r...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (December 2020) (Learn how and when to remove this template message) This article relies largely or entirely on a single source. Relevant discussion m...

9th episode of the 4th season of Hannah Montana I'll Always Remember YouHannah Montana episodeMiley realizes that Lilly and Jesse hate what the secret has done to their lives.Episode no.Season 4Episode 9Directed byBob Koherr (part 1)Shannon Flynn (part 2)Written byMaria Brown-GallenbergAndrew GreenProduced bySteven PetermanMichael PoryesFeatured musicsee musicCinematography byAlan Keath WalkerEditing byKenny TintorriProduction code409-410Original air dateNovember 7, 2010 (...

1941 film by Alexandr Hackenschmied The Forgotten VillageTheatrical release posterDirected byHerbert KlineAlexander HammidScreenplay byJohn SteinbeckStory byJohn SteinbeckProduced byAlexander HammidHerbert KlineNarrated byBurgess MeredithCinematographyAlexander HammidEdited byHerbert KlineMusic byHanns EislerDistributed byArthur Mayer & Joseph BurstynRelease dates 9 September 1941 (1941-09-09) (New York City) 18 November 1941 (1941-11-18) (U.S.) Runni...





![{\displaystyle \phi [B]X_{t}=\varepsilon _{t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/427fcdc777a1ef12ec7498f413bfbcb6d0932af5)