โน้ตดนตรี
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

You can help expand this article with text translated from the corresponding article in Italian. (January 2022) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or lo...

ДостопримечательностьПамятник бойцам Первой конной армииПам'ятник бійцям Першої кінної армії 49°57′55″ с. ш. 24°55′37″ в. д.HGЯO Страна Украина Местоположение недалеко от села Хватов и посёлка Олеско, Бусский район Львовская область Дата основания 21 декабря 1975 Д

Vincenzo Giuffrida Ministro delle poste del Regno d'ItaliaDurata mandato4 luglio 1921 –26 febbraio 1922 MonarcaVittorio Emanuele III di Savoia Capo del governoIvanoe Bonomi PredecessoreRosario Pasqualino Vassallo SuccessoreGiovanni Antonio Colonna di Cesarò LegislaturaXXVI Deputato del Regno d'ItaliaLegislaturaXXV, XXVI, XXVII Sito istituzionale Dati generaliTitolo di studioLaurea in Giurisprudenza Professionefunzionario amministrativo Vincenzo Giuffrida (Ca...

Main US-oriented communications officer for foreign policy decisionmakers United StatesAssistant Secretary of Statefor Public AffairsSeal of the United States Department of StateReports toThe Under Secretary for Public Diplomacy and Public AffairsAppointerThe President of the United StatesInaugural holderArchibald MacLeishFormation1944AbolishedMay 28, 2019SuccessionAssistant Secretary of State for Global Public AffairsWebsiteOfficial Website The Assistant Secretary of State for Public Affairs...

Cet article est une ébauche concernant une exoplanète. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Gliese 581 e Vue d'artiste de Gliese 581 e Étoile Nom Gliese 581 Constellation Balance Ascension droite 15h 19m 26s Déclinaison −07° 43′ 20″ Type spectral M3 Localisation dans la constellation : Balance Caractéristiques orbitales Demi-grand axe (a) 0,03 ua Excen...

Міжкратерні рівнини на Меркурії — форма рельєфу, що складається з рівнин між кратерами на Меркурії. Міжкратерні рівнини і сильно порізаний кратерами рельєф характерні для більшої частини Меркурія за межами області, на яку вплинуло формування басейну Калоріс. На рівни

1987 greatest hits album by George StraitGreatest Hits Volume TwoGreatest hits album by George StraitReleasedSeptember 7, 1987 (1987-09-07)Recorded1984-87GenreCountryLength30:35LabelMCA RecordsMCAD-42035Producer Jimmy Bowen George Strait George Strait chronology Ocean Front Property(1987) Greatest Hits Volume Two(1987) If You Ain't Lovin' You Ain't Livin'(1988) Professional ratingsReview scoresSourceRatingAllmusic [1]Robert ChristgauB [2] Greatest Hits V...

Cet article est une ébauche concernant une peintre américaine et l’art contemporain. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Jane HammondNaissance 1950BridgeportNationalité américaineActivité Peinture, Dessin, collageFormation Université du Wisconsin à MadisonMount Holyoke CollegeReprésentée par Galerie Lelong (d)Influencée par John CageDistinctions Prix Anonymous Was A Woman (2013)Bours...

Se ha sugerido que «Lugo (Asturias)» sea fusionado en este artículo o sección. Motivo: los argumentos están expuestos en la página de discusión.Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí.Este aviso fue puesto el 2 de junio de 2016. Lugo de LlaneraLa Estación/ Lugo de Llanera Estación Lugo de Llanera (Asturias) Coordenadas 43°26′32″N 5°49′06″O / 43.442279, -5.818441Entidad Estación • País España �...

此條目没有列出任何参考或来源。 (2023年12月5日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 我们恋爱吧 (第三季)The Relationship 3类型真人實境秀、綜藝節目总导演郝煒晨主持张纯烨、伊能静、張繼科、朱正廷、宋雨琦、姜振宇制作国家/地区 中国语言普通話季数5集数12集每集长度約85分鐘制�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2016 D.C. United season – news · newspapers · books · scholar · JSTOR (March 2016) (Learn how and when to remove this template message) D.C. United 2016 soccer seasonD.C. United2016 seasonGeneral managerDave KasperHead coachBen OlsenStadiumRFK StadiumMLSConfere...

石川県立大聖寺実業高等学校 北緯36度17分52.9秒 東経136度18分17.4秒 / 北緯36.298028度 東経136.304833度 / 36.298028; 136.304833座標: 北緯36度17分52.9秒 東経136度18分17.4秒 / 北緯36.298028度 東経136.304833度 / 36.298028; 136.304833国公私立の別 公立学校設置者 石川県学区 全県一学区校訓 誠実・友愛・創造設立年月日 1965年9月創立記念日 11月12日共学・別�...

كارينيو (بالإسبانية: Cariño)[1] - بلدية - كارينيو (لا كرونيا) كارينيو (لا كرونيا) خريطة الموقع تقسيم إداري البلد إسبانيا [2] المقاطعة مقاطعة لا كورونيا خصائص جغرافية إحداثيات 43°44′29″N 7°52′09″W / 43.741388888889°N 7.8691666666667°W / 43.741388888889; -7.869...

إسيكييل بالاسيوس معلومات شخصية الميلاد 5 أكتوبر 1998 (العمر 25 سنة) الطول 1.77 م (5 قدم 9 1⁄2 بوصة) مركز اللعب وسط الجنسية الأرجنتين معلومات النادي النادي الحالي باير 04 ليفركوزن الرقم 25 مسيرة الشباب سنوات فريق 0000–2015 ريفر بليت المسيرة الاحترافية1 سنوات فريق م. (هـ.) 201...

GPIB Immanuel DKI JakartaGereja Protestan di Indonesia bagian BaratGedung Gereja Immanuel, JakartaLokasiJakarta, IndonesiaDenominasiCalvinisArsitekturStatus fungsionalAktifPenetapan warisanAArsitekJ.H. HorstTipe arsitekturGerejaAdministrasiKeuskupanMupel Jakarta PusatKlerusPastorPdt. Abraham Ruben Persang Cagar budaya IndonesiaGereja ImmanuelPeringkatNasionalKategoriBangunanNo. RegnasRNCB.19880227.02.000623LokasikeberadaanJakarta Pusat, JakartaTanggal SK1999, 1993 & 2017PemilikGereja Prot...

See also: Ultra Music Festival Ultra SingaporeGenreElectronic dance musicDate(s)Early- to mid- June(since 2017)FrequencyAnnuallyLocation(s)Marina Bay, SingaporeYears active8 yearsInauguratedSeptember 19, 2015 (2015-09-19)Most recentJune 8-9, 2019Attendance41,000 (2018)Websiteultrasingapore.com A picture of the Ultra Singapore Stage. Ultra Singapore is an outdoor electronic music festival that debuted in 2015 in Singapore as part of Ultra Music Festival's worldwide expansion, wh...

Final Piala Liga Inggris 1977TurnamenPiala Liga Inggris 1976–1977 Aston Villa Everton Aston Villa Everton 0 0 Tanggal12 Maret 1977StadionStadion Wembley, LondonWasitGordon Kew (Leeds)Penonton100.000Pertandingan ulangan Everton Aston Villa 1 1 setelah perpanjangan waktuTanggal16 Maret 1977StadionStadion Hillsborough, SheffieldWasitGordon Kew (Leeds)Penonton55.000Pertandingan ulangan kedua Everton Aston Villa 2 3 setelah perpanjangan waktuTanggal13 April 1977LokasiOld Trafford, ManchesterWasi...

South African cricketer For other people named David Miller, see David Miller (disambiguation). David MillerMiller during a training session in 2014Personal informationFull nameDavid Andrew MillerBorn (1989-06-10) 10 June 1989 (age 34)Pietermaritzburg, Kwa-Zulu Natal, South AfricaHeight1.80 m (5 ft 11 in)BattingLeft-handedBowlingRight-arm off breakRoleMiddle-order batterInternational information National sideSouth Africa (2010–present)ODI debut (cap 98)22 M...
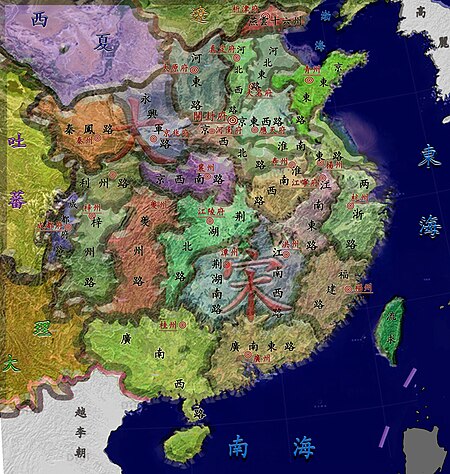
邠州在陕西省的位置(1820年) 邠(bīn)州,中国古代设置的一个州,治所在今陕西省彬州市。 唐朝开元十三年(725年),以豳州的“豳(bīn)”字和幽州的“幽”字形相近,豳州改名邠(bīn)州。治新平县(今陕西彬县)。属关内道。辖境约当今陕西省彬州市、长武县、旬邑县、永寿县等县地。唐朝后期为邠宁节度使治所。明朝废新平县入邠州。清朝雍正三年(1725年)�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (�...








