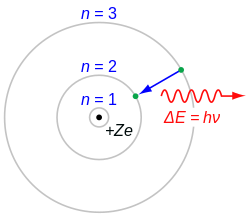
Паулијев принцип
|
Read other articles:

وزارة استيعاب المهاجرين (إسرائيل) وزارة استيعاب المهاجرين (إسرائيل) تفاصيل الوكالة الحكومية البلد إسرائيل تأسست 1948 المركز تل أبيب32°05′07″N 34°46′54″E / 32.0853°N 34.781768°E / 32.0853; 34.781768 الإدارة منصب المدير وزير استيعاب المهاجرين [لغات أخرى] موقع ا

الذفر (محلة) تقسيم إداري البلد اليمن المحافظة محافظة إب المديرية مديرية السبرة العزلة عزلة مطاية القرية قرية مطاية السكان التعداد السكاني 2004 السكان 26 • الذكور 13 • الإناث 13 • عدد الأسر 3 • عدد المساكن 2 معلومات أخرى التوقيت توقيت اليمن (+3 غرينيتش) تعديل مص�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2022) معركة سفاكتيريا جزء من حرب الاستقلال اليونانية Sortie of the Aris خلال حصار الأسطول العثماني بأكمله لنافارينو في 25 أبريل 1825 بواسطة كونستانتينوس فولاناكيس معلومات ع

دوار الحجامين تقسيم إداري البلد المغرب الجهة فاس مكناس الإقليم تاونات الدائرة غفساي الجماعة القروية تابودة المشيخة أولاد بن راشد و بني عبد الله السكان التعداد السكاني 187 نسمة (إحصاء 2004) • عدد الأسر 36 معلومات أخرى التوقيت ت ع م±00:00 (توقيت قياسي)[1]، وت ع م+01:00 (تو�...

Major women's suffrage organizations International International Alliance of Women – founded in 1904 to promote women's suffrage. Woman's Christian Temperance Union – active in the suffrage movement, especially in the U.S. and New Zealand. Australia Victorian Women's Suffrage Society, founded in 1884, the local suffrage organisation of Victoria and the first suffrage organisation in Australia Belgium Ligue belge du droit des femmes (Belgian League for the Rights of Women), founded 1892, c...

الغزو الإسباني لإمبراطورية إنكا جزء من الاستعمار الإسباني للأمريكتين الغزو الإسباني للبيرو معلومات عامة التاريخ 1532–1572 الموقع غرب أمريكا الجنوبية13°31′20″S 71°59′00″W / 13.522222°S 71.983333°W / -13.522222; -71.983333 النتيجة انتصار اسبانيا, اعدام الماضي إنكا سابا أتاوالب�...

Dirk Bach, Moderation des Life Ball 2009 Dirk Bach (* 23. April 1961 in Köln; † 1. Oktober 2012 in Berlin[1]) war ein deutscher Schauspieler, Synchronsprecher, Entertainer, Moderator und Komiker. Inhaltsverzeichnis 1 Leben 1.1 Privatleben und gesellschaftliches Engagement 1.2 Tod 2 Auszeichnungen 3 Filmografie 3.1 Filme 3.2 Fernsehsendungen 4 Theater 5 Buch 6 Hörbücher 7 Literatur 8 Einzelnachweise 9 Weblinks Leben Dirk Bach mit Hella von Sinnen beim Benefiz-Konzert Cover me in K...

Campeonato BrasileñoSerie C 2023Brasileirão Série C 2023 Arena das Dunas de Natal. Volvió a recibir partidos de la Serie C siete años después.Datos generalesSede BrasilFecha 2 de mayo al22 de octubreEdición 33.ªPalmarésCampeón Amazonas (1.° título)Subcampeón BrusqueDatos estadísticosParticipantes 20 equiposPartidos 216Goles 465 (2.15 por partido)Mayor anotador Sassá (18 goles) (Amazonas FC) Intercambio de plazas Ascenso(s): Amazonas Brusque Operário Ferroviário Paysandu Desce...

Private Christian college in Roseville, Minnesota, U.S. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Northwestern – St. Paul – news · newspapers · books · scholar · JSTOR (June 2008) (Learn how and when to remove this template message) University of NorthwesternFormer namesNorthwestern Bib...

American book publisher St. Martin's PressParent companyMacmillan PublishersFounded1952; 71 years ago (1952)Country of originUnited StatesHeadquarters locationEquitable Building120 BroadwayNew York City, New York 10271, U.S.DistributionMacmillan (US)Melia Publishing Services (UK)[1]Key peopleGeorge WitteSally Richardson[2]Jennifer EnderlinAndrew MartinLaura ClarkImprintsCastle Point Books, Griffin, Minotaur, St. Martin's Press, St. Martin's Essentials, Wednes...

Danish businessman and founder of The Lego Group Ole Kirk ChristiansenFounder and 1st Leader of The Lego GroupIn office10 August 1932 (1932-08-10) – 11 March 1958 (1958-03-11)Succeeded byGodtfred Kirk Christiansen Personal detailsBorn(1891-04-07)7 April 1891Omvraa Mark, Filskov, South Jutland, DenmarkDied11 March 1958(1958-03-11) (aged 66)Billund, DenmarkCause of deathCardiac arrestResting placeBillund, DenmarkSpouses Kirstine Sörensen ...

Notion PressTypePrivateIndustrySelf-publishingFounded2012HeadquartersChennai, IndiaKey peopleBhargava Adepally Naveen Valsakumar Jana PillayProductsBooksWebsitenotionpress.com Notion Press is an Indian self-publishing company based in Chennai, India. It was founded in 2012,[1] and in 2016 it claimed to have provided services to 2000 self-published authors.[2] In 2018, they introduced a rapid publication service, which does not include editing.[3] History Notion Press w...

1992 killing of peasants in Peru This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Santa massacre – news · newspapers · books · scholar · JSTOR (December 2012) (Learn how and when to remove this template message) For the 2008 massacre perpetrated by a man in a Santa Claus suit, see Covina massacre. Santa massa...

1946 film Iris and the LieutenantFilm posterDirected byAlf SjöbergWritten byOlle HedbergAlf SjöbergProduced byHarald MolanderStarringMai ZetterlingRelease date 16 December 1946 (1946-12-16) Running time86 minutesCountrySwedenLanguageSwedish Iris and the Lieutenant (Swedish: Iris och löjtnantshjärta) is a 1946 Swedish drama film directed by Alf Sjöberg and starring Mai Zetterling, Alf Kjellin and Åke Claesson.[1] The film boosted Zetterling's international profile....

Perwira KNIL dalam pengawalan menuju istana pada tahun 1874. Perang Aceh Kedua diumumkan oleh KNIL terhadap Aceh pada tanggal 20 November 1873 setelah kegagalan serangan pertama. Pada saat itu, Belanda sedang mencoba menguasai seluruh Nusantara. Ekspedisi yang dipimpin oleh Jan van Swieten itu terdiri atas 8.500 prajurit, 4.500 pembantu dan kuli, dan belakangan ditambahkan 1.500 pasukan. Pasukan Belanda dan Aceh sama-sama menderita kolera. Sekitar 1.400 prajurit kolonial meninggal antara bula...

Este artículo o sección sobre geografía necesita ser wikificado, por favor, edítalo para que cumpla con las convenciones de estilo.Este aviso fue puesto el 13 de octubre de 2009. Distrito de Chongos Bajo Distrito del Perú Coordenadas 12°07′59″S 75°16′06″O / -12.1330053, -75.2682996Capital Chongos BajoIdioma oficial español • Co-oficiales quechuaEntidad Distrito del Perú • País Perú Perú • Departamento Junín • Provincia ChupacaAl...

Montenegrin basketball player Petar PopovićPopović with Budućnost in 2023.No. 30 – Budućnost VOLIPositionPoint guard / shooting guardLeagueABA LeagueMontenegrin LeaguePersonal informationBorn (1996-09-13) 13 September 1996 (age 27)Cetinje, Montenegro, FR YugoslaviaNationalityMontenegrinListed height1.92 m (6 ft 4 in)Listed weight87 kg (192 lb)Career informationNBA draft2018: undraftedPlaying career2011–presentCareer history2011–2014Lovćen Cetin...

Overview of the electricity sector in Germany Electricity sector of GermanyDataContinuity of supply0.2815 h (16.89 min) interruption per subscriber per yearInstalled capacity (2020)211.31 GW[1]Production (2021)490.6 TW⋅h[2]Share of fossil energy40.9% (2021)[2]Share of renewable energy45.8% (2021)[2]GHG emissions from electricity generation (2013)363.7 Mt CO2 [631.4 TW⋅h × 576 g/kW⋅h]Tariffs and financingA...

2011 film by Henry Joost and Ariel Schulman Paranormal Activity 3Theatrical release posterDirected by Henry Joost Ariel Schulman Written byChristopher LandonProduced by Jason Blum Oren Peli Steven Schneider Starring Lauren Bittner Chris Smith Chloe Csengery Jessica Tyler Brown Katie Featherston CinematographyMagdalena GorkaEdited byGregory PlotkinProductioncompanyBlumhouse ProductionsDistributed byParamount PicturesRelease dates October 14, 2011 (2011-10-14) (Rio de Janeiro...

Acting president of Harvard University Eliphalet Pearson1st Preceptor of Phillips AcademyIn office1778–1786Preceded byoffice establishedSucceeded byEbenezer PembertonActing President of Harvard UniversityIn office1804–1806Preceded byJoseph WillardSucceeded bySamuel Webber Personal detailsBornEliphalet Pearson(1752-06-11)June 11, 1752Newbury, MassachusettsDiedSeptember 12, 1826(1826-09-12) (aged 74)Greenland, New HampshireEducationThe Governor's AcademyHarvard College, 1773 Eliphalet ...