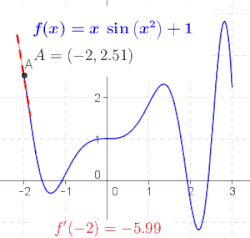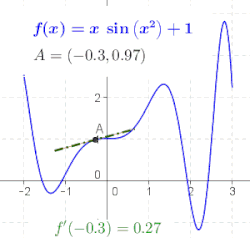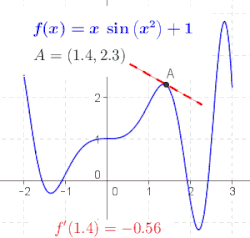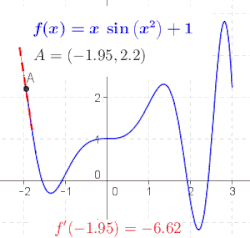
Diferencijalni račun
|
Read other articles:

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Gugatan der...

Berikut ini adalah daftar stasiun radio siaran berdasarkan kabupaten di Provinsi Riau. Bengkalis Logo Radio Frekuensi Jaringan RRI Pro 1 Bengkalis 90.6 FM RRI Pro 1 dan Voice of Indonesia Indra Bengkalis 88.2 FM Independen Patra Duri 93.6 FM Unimax Power Kabupaten Kampar Logo Radio Frekuensi Jaringan Robbani 91.1 FM Independen Persada FM 93.2 FM Persada FM Rama 96.3 FM Independen Utama 97.1 FM Independen LPPL Suara Kampar 103.8 FM Persada ID dan Voice of Indonesia Radio Markaz 88 FM Independe...

Grand Prix Republik ArgentinaGrand Prix Sepeda MotorTempatAutódromo Termas de Río HondoLomba pertama1960Terbanyak menang (rider)Hugh Anderson, Mick Doohan, Tom Phillis (3)Terbanyak menang (pabrikan)Honda (12) Grand Prix Sepeda Motor Argentina merupakan seri dari kejuaraan balap FIM Grand Prix Sepeda Motor. Acara ini telah diadakan sepuluh kali di Autódromo Oscar Alfredo Gálvez antara musim 1961 dan 1999. Grand Prix Argentina kembali menjadi tuan rumah penyelenggaraan MotoGP pada musim 201...

Dieser Artikel behandelt den Tierkreis. Für das gleichnamige Musikalbum der Rapper RAF Camora und Chakuza siehe Zodiak (Album). Für andere Bedeutungen von Zodiak und Zodiac siehe Zodiac. SCENOGRAPHIA SYSTEMATIS MVNDANI PTOLEMAICI, Andreas Cellarius: Harmonia Macrocosmica. 1660/61 Als Zodiak, auch Zodiakus (zu lateinisch zodiacus, von altgriechisch ζῳδιακός zōdiakós) oder deutsch Tierkreis, wird heute eine etwa 20 Grad breite Zone um die Ekliptik, also die scheinbare Sonnenba...

Maltese musical band The TravellersThe Travellers live at the Għaxaq Music festival in July 2022Background informationOriginGozo, MaltaGenresPop musicYears active2013–presentMembers Clayton Bonello (bass guitar) Joseph Xerri (trumpet) Chris Gatt (vocals) Andrew Vella (guitar & backing vocals) Sylvano Mizzi (saxophone & keyboards) Michael Camilleri (drums) Websitewww.thetravellersmalta.com The Travellers are a music band from the Maltese island of Gozo. They released Sempliċità (S...

Untuk perenang, lihat Kim Hyun-joo (perenang). Kim Hyun-jooKim pada tahun 2018Lahir24 April 1977 (umur 46)Goyang, Provinsi Gyeonggi, Korea SelatanPendidikanUniversitas Dankook – Teater dan FilmPekerjaanAktrisTahun aktif1996–sekarangAgenYNK Entertainment[1]Nama KoreaHangul김현주 Hanja金賢珠 Alih AksaraKim Hyeon-juMcCune–ReischauerKim Hyŏnju Dalam artikel ini, nama keluarganya adalah Kim. Kim Hyun-joo (lahir 24 April 1977)[2] adalah aktris asal Korea Selat...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Agustus 2017. Alfons TaryadiLahir(1936-05-11)11 Mei 1936 Klaten, Jawa Tengah,IndonesiaMeninggal18 Mei 2013(2013-05-18) (umur 77) Jakarta, IndonesiaPekerjaansastrawaneditorKebangsaan Indonesia Alfons Taryadi (11 Mei 1936 – 18 Mei 2013) adalah sas...

Manchester Metrolink tram stop Etihad CampusMetrolink stationThe stop in May 2019.General informationLocationEtihad Campus/Sportcity, ManchesterEnglandCoordinates53°29′07″N 2°12′05″W / 53.48537°N 2.20134°W / 53.48537; -2.20134Line(s)East Manchester LinePlatforms2Other informationStatusIn operationFare zone2HistoryOpened8 February 2013 (preview)[1]11 February 2013 (full)[2][3]Original companyMetrolinkRoute map Legend to MediaCity...

Mapa kun diin makikit-an an mga lalawigan han Rehiyon han Veneto An Veneto amo an usa (1) ha karuhaan (20) ka rehiyon han Italya. An ulohan hini amo an Venesya. Mga lalawigan han Veneto Belluno Padua Rovigo Treviso Venesya Verona Vicenza khlMga Rehiyon han Italya AbruzzoSiong han AostaApuliaBasilicata CalabriaCampaniaEmilia-RomagnaFriuli-Venezia Giulia LazioLiguriaLombardiyaMarche MolisePiemonteSardinyaSicilia Trentino-Alto Adige/SüdtirolToscanaUmbriaVeneto Usa ka tur...

Ankhesenamun, yang dianggap sebagai ratu Mesir yang mengundang Suppiluliuma I untuk mengirim putranya Zannanza untuk menjadi istrinya Zannanza (meninggal skt. 1324 SM) merupakan seorang pangeran Het, putra Suppiluliuma I, raja Het. Ia terkenal karena hampir menjadi firaun Mesir, dan karena kematiannya menimbulkan insiden diplomatik di antara keluarga Het dan kerajaan Mesir, yang mengakibatkan peperangan. Ratu Mesir Dakhamunzu, yang mungkin saja Meritaten atau Nefertiti, tapi paling sering dii...

Distrik Kolubara Колубарски округ Kolubarski okrugDistrik SerbiaLetak Distrik Kolubara di SerbiaNegara SerbiaPusat administratifValjevoPemerintahan • Komisionern/aLuas • Total2,474 km2 (955 sq mi)Populasi (Sensus 2011) • Total174,228 • Kepadatan70,4/km2 (182/sq mi)Munisipalitas Serbia5 dan 1 kotaPermukiman218- Kota7- Desa211 Distrik Kolubara (bahasa Serbia: Колубарски округ, Kolubar...

Voce principale: Castiglia-La Mancia. Presidente della Giunta delle Comunità di Castiglia-La Mancia Emiliano García-Page, in carica dal 4 luglio 2015 Nome originalePresidente de la Junta de Comunidades de Castilla-La Mancha Stato Spagna Comunità autonoma Castiglia-La Mancia TipoCapo del governo regionale In caricaEmiliano García-Page (PSOE) da4 luglio 2015 Istituito6 giugno 1983 Nominato daCorti di Castiglia-La Mancia /Re di Spagna Durata mandato4 anni SedePalazzo di Fuensalida,...

Book by Nasreen Munni Kabir Yours Guru Dutt AuthorNasreen Munni KabirCountryIndiaLanguageEnglishSubjectGuru DuttGenreBiographyPublished2006PublisherRoli BooksMedia typePrintPages168ISBN978-81-74363-88-6OCLC494710408 Yours Guru Dutt is a 2006 book by the British author and television documentary producer Nasreen Munni Kabir, containing a total of 37 handwritten letters in both English and Hindi by the Indian actor and filmmaker Guru Dutt—most of which are addressed to his wife Geeta. Th...

Sonar (Singkatan dari bahasa Inggris: sound navigation and ranging), merupakan istilah Amerika yang pertama kali digunakan semasa Perang Dunia, yang berarti penjarakan dan navigasi suara, adalah sebuah teknik yang menggunakan penjalaran suara dalam air untuk navigasi atau mendeteksi kendaraan air lainnya. Sementara itu, Inggris punya sebutan lain untuk sonar, yakni ASDIC (Anti-Submarine Detection Investigation Committee). Cara kerja AN-PQS 2A hand held sonar Sonar merupakan sistem yang menggu...

Major lake in Switzerland This article is about the lake in Switzerland. For the lake and village in the U.S., see Lake Zurich, Illinois. For the Gorillaz song, see The Now Now. Lake ZurichZürichsee (German)Lake Zürich, Pfannenstiel, and Sihl Valley, as seen from nearby Felsenegg in April 2010Lake ZurichShow map of Canton of ZurichLake ZurichShow map of Canton of SchwyzLake ZurichShow map of Canton of St. GallenLake ZurichShow map of SwitzerlandLake ZurichShow map of AlpsCoordinates47�...

1956 film Against AllFilm poster (Bulgarian release)Directed byOtakar VávraWritten by Alois Jirásek Milos Václav Kratochvíl Otakar Vávra StarringZdeněk ŠtěpánekRelease date 1956 (1956) Running time109 minutesCountryCzechoslovakiaLanguageCzechBudget25 million KČs[1] Against All (Czech: Proti všem) is a 1956 Czechoslovak historical drama film directed by Otakar Vávra.[2] It is based on the novel Proti všem by Alois Jirásek. The film's budget was 25 million KČ...

Waterbody in Navajo County, Arizona Fool Hollow LakeFool Hollow LakeLocationNavajo County, ArizonaCoordinates34°16′15″N 110°04′07″W / 34.2707663°N 110.0685947°W / 34.2707663; -110.0685947[1]Basin countriesUnited StatesSurface area150 acres (61 ha)Average depth23 ft (7.0 m)Surface elevation6,260 ft (1,910 m) Fool Hollow Lake is a public lake located in Navajo County, Arizona, near the city of Show Low. The lake is operat...

Railway station in South Yorkshire, England Kiveton BridgeThe station in 2008General informationLocationKiveton Park, RotherhamEnglandCoordinates53°20′26″N 1°15′57″W / 53.340460°N 1.265750°W / 53.340460; -1.265750Grid referenceSK489828Managed byNorthern TrainsTransit authorityTravel South YorkshirePlatforms2Other informationStation codeKIVFare zoneRotherhamClassificationDfT category F2HistoryOpened1929Passengers2017/18 62,4242018/19 67,6302019/20 76,7722020...

Letak penemuan kebudayaan Atestina di sebelah selatan kebudayaan Hallstatt. Situla yang ditemukan di Vače, Slovenia. Kebudayaan Atestina (juga disebut sebagai kebudayaan Este atau Paleo-Venetia) adalah kebudayaan arkeologi Zaman Besi (abad ke-10 hingga ke-9 SM, tahap awal Proto-Venetia) yang ditemukan di Veneto, Semenanjung Italia. Kebudayaan ini merupakan kelanjutan dari Kebudayaan Proto-Villanova.[1] Kebudayaan ini juga sering disebut sebagai Peradaban Situla. Kebudayaan ini dinama...
Seckach Die Seckach unterhalb von Sennfeld Die Seckach unterhalb von Sennfeld Daten Gewässerkennzahl DE: 23886 Lage Odenwald Sandsteinodenwald Lohrbacher Vorstufen Bauland Schefflenzgäu Mittleres Bauland Seckach-Kirnau-Platten Kocher-Jagst-Ebenen Neudenauer Hügel Westliche Kocher-Jagst-Ebenen Seckach-Kessach-Riedel Jagsttal Unteres Jagsttal[1][2] Baden-Württemberg Neckar-Odenwald-Kreis Landkreis Heilbronn Flusssystem Rhein Abfluss über ...