–§—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞, —Б–Ї—А. –§–Ю–Я (–µ–љ–≥. Optical transfer function, OTF) —Ш–µ —Б–ї–Њ–ґ–µ–љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–Ї–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Ї–Њ—Ш–∞ –Њ–њ–Є—Б—Г—Ш–µ –Њ–њ—В–Є—З–Ї—Г —Б–ї–Є–Ї—Г –Њ–±—Ш–µ–Ї—В–∞ —З–Є—Ш–∞ –њ–Њ–≤—А—И–Є–љ–∞ —Ш–µ –±–µ—Б–Ї—А–∞—Ш–∞–љ –љ–Є–Ј –њ–∞—А–∞–ї–µ–ї–љ—Е —Б–≤–µ—В–ї–Є—Е –Є —В–∞–Љ–љ–Є—Е –ї–Є–љ–Є—Ш–∞ —Б–∞ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Є–Љ —А–∞—Б–њ–Њ—А–µ–і–Њ–Љ –Ј—А–∞—З–µ—Ъ–∞. –Ь–∞–і–∞ –§–Ю–Я –Њ–њ–Є—Б—Г—Ш–µ —Б–ї–Є–Ї—Г —Б–∞–Љ–Њ –Њ–≤–µ —Ш–µ–і–љ–µ –≤—А—Б—В–µ –Њ–±—Ш–µ–Ї—В–∞, —Б–Љ–∞—В—А–∞ —Б–µ –Њ–њ—И—В–Є–Љ –њ–Њ–Ї–∞–Ј–∞—В–µ—Щ–µ–Љ –љ–Є–≤–Њ–∞ –Ї–∞–Ї–≤–Њ—Ы–µ —Д–Є–Ј–Є—З–Ї–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ.[1] –У—А–∞—Д–Є—З–Ї–Є –њ—А–Є–Ї–∞–Ј –§–Ю–Я, –љ–∞—Ш—З–µ—И—Ы–µ —Г –≤–Є–і—Г —Ъ–µ–љ–Њ–≥ –і–µ–ї–∞ –Ї–Њ—Ш–Є –Њ–њ–Є—Б—Г—Ш–µ –Њ—И—В—А–Є–љ—Г —Б–ї–Є–Ї–µ (—Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ, –§–Я–Т), —Ш–µ –љ–µ–њ–Њ—Б—А–µ–і–∞–љ, –ї–∞–Ї–Њ —А–∞–Ј—Г–Љ—Щ–Є–≤ –њ–Њ–Ї–∞–Ј–∞—В–µ—Щ –Ї–∞–Ї–≤–Њ—Ы–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ. –Ч–±–Њ–≥ —В–Њ–≥–∞ —Ш–µ —Г —И–Є—А–Њ–Ї–Њ—Ш —Г–њ–Њ—В—А–µ–±–Є –Ї–∞–Ї–Њ —Г –Њ–њ—В–Є—З–Ї–Є–Љ —Г—Я–±–µ–љ–Є—Ж–Є–Љ–∞ –Є –њ—Г–±–ї–Є–Ї–∞—Ж–Є—Ш–∞–Љ–∞, —В–∞–Ї–Њ –Є —Г —Б—Д–µ—А–Є –њ—А–Њ–Є–Ј–≤–Њ–і—Ъ–µ –Њ–њ—В–Є—З–Ї–Є—Е –Є–љ—Б—В—А—Г–Љ–µ–љ–∞—В–∞.
–£ –Ј–∞–≤–Є—Б–љ–Њ—Б—В–Є –Њ–і –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ –Ї–Њ—Ш—Г –Ї–Њ—А–Є—Б—В–Є –Ј–∞ –њ—А–Њ—А–∞—З—Г–љ, –§–Ю–Я –Љ–Њ–ґ–µ –±–Є—В–Є –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–∞ –Є –≥–µ–Њ–Љ–µ—В—А–Є—Ш—Б–Ї–∞. –Я—А–≤–∞ –Ї–Њ—А–Є—Б—В–Є –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ—Г, —В—Ш. —Д–Є–Ј–Є—З–Ї—Г –Њ–њ—В–Є—З–Ї—Г —Б–ї–Є–Ї—Г, –∞ –і—А—Г–≥–∞ –≥–µ–Њ–Љ–µ—В—А–Є—Ш—Б–Ї—Г —Б–ї–Є–Ї—Г –∞–±–µ—А–∞—Ж–Є—Ш–µ, —В—Ш. –Ј–∞—Б–љ–Є–≤–∞ —Б–µ –љ–∞ —А–∞—Б–њ–Њ—А–µ–і—Г —В–∞—З–∞–Ї–∞ –Ј—А–∞–Ї–∞, –Ч–∞ —А–∞–Ј–ї–Є–Ї—Г –Њ–і –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–µ –§–Ю–Я, –≥–µ–Њ–Љ–µ—В—А–Є—Ш—Б–Ї–∞ –§–Ю–Я –Є–Љ–∞ —Б–∞–Љ–Њ –Њ–≥—А–∞–љ–Є—З–µ–љ—Г —Г–њ–Њ—В—А–µ–±—Г. –Я—А–µ–і–Љ–µ—В –і–∞—Щ–µ–≥ —В–µ–Ї—Б—В–∞ —Ш–µ –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–∞ –§–Ю–Я.
–Ю–њ–Є—Б —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞
–§–Ю–Я —Б–µ –Љ–Њ–ґ–µ –Њ–њ–Є—Б–∞—В–Є –Ї—А–Њ–Ј –Њ–њ–Є—Б —Ъ–µ–љ–Є—Е —Б—Г–±—Ш–µ–Ї–∞—В–∞ - —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ –Њ–±—Ш–µ–Ї—В–∞ –Є —Ъ–µ–≥–Њ–≤–µ —Б–ї–Є–Ї–µ - –Ї—А–Њ–Ј –Њ–±–ї–Є–Ї —Г –Ї–Њ–Љ–µ —Б–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ —А–µ–Ј—Г–ї—В–∞—В –і–Њ –Ї–Њ–≥ —Б–µ —Ъ–Њ–Љ–µ –і–Њ–ї–∞–Ј–Є –Є, –љ–∞—Ш–Ј–∞–і, –Ї—А–Њ–Ј –љ–∞—З–Є–љ –љ–∞ –Ї–Њ—Ш–Є —Б–µ –і–Њ –Њ–≤–Є—Е —А–µ–Ј—Г–ї—В–∞—В–∞ –і–Њ–ї–∞–Ј–Є, —В—Ш. —Ъ–µ–љ –Љ–∞—В–µ–Љ–∞—В–Є—З–Ї–Є –Њ–±–ї–Є–Ї –Є –њ–Њ—Б—В—Г–њ–∞–Ї.
–Ю–±—Ш–µ–Ї—В —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞
–§–Ю–Я –љ–µ –Ї–Њ—А–Є—Б—В–Є —Б—В–≤–∞—А–љ–Є –Њ–±—Ш–µ–Ї—В, –љ–µ–≥–Њ —Ъ–µ–≥–Њ–≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–Ї–Є –Њ–±–ї–Є–Ї. –Ю–≤–∞—Ш –Њ–±—Ш–µ–Ї—В —Ш–µ –љ–µ–њ—А–µ–Ї–Є–і–љ–∞ —Б–Є–љ—Г—Б–Њ–Є–і–љ–∞ –њ—А–Њ–Љ–µ–љ–∞ —Ш–∞—З–Є–љ–µ –Ј—А–∞—З–µ—Ъ–∞, —В—Ш. –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ —Ш–µ –±–µ—Б–Ї—А–∞—Ш–љ–Є–Љ –љ–Є–Ј–Њ–Љ —В–∞–Љ–љ–Є—Е –Є —Б–≤–µ—В–ї–Є—Е –ї–Є–љ–Є—Ш–∞, —З–Є—Ш–Є —Б—Ш–∞—Ш —Б–µ –њ–Њ—Б—В–µ–њ–µ–љ–Њ –Љ–µ—Ъ–∞ –Њ–і –љ–∞—Ш–≤–Є—И–µ–≥ (—Г —Б—А–µ–і–Є–љ–Є —Б–≤–µ—В–ї–µ –ї–Є–љ–Є—Ш–µ) –і–Њ –љ–∞—Ш–љ–Є–ґ–µ–≥ (—Б—А–µ–і–Є–љ–∞ —В–∞–Љ–љ–µ –ї–Є–љ–Є—Ш–µ). –®–Є—А–Є–љ–∞ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ –њ–µ—А–Є–Њ–і–∞, —В—Ш. —И–Є—А–Є–љ–∞ —Б–≤–µ—В–ї–Є—Е –Є —В–∞–Љ–љ–Є—Е –ї–Є–љ–Є—Ш–∞ —Б–µ –Ї—А–µ—Ы–µ —Г —А–∞—Б–њ–Њ–љ—Г –Њ–і –±–µ—Б–Ї–Њ–љ–∞—З–љ–Њ —И–Є—А–Њ–Ї–Є—Е –і–Њ –±–µ—Б–Ї–Њ–љ–∞—З–љ–Њ —Г—Б–Ї–Є—Е. –Р–Ї–Њ —Б—Г –Њ—Б–Њ–±–Є–љ–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ –њ–Њ–Ј–љ–∞—В–µ, –њ—Г—В–µ–Љ –§–Ю–Я —Б–µ –і–Њ–ї–∞–Ј–Є –і–Њ —Б–≤–Њ—Ш—Б—В–∞–≤–∞ —Б–ї–Є–Ї–µ –Ї–Њ—Ш—Г –Њ–љ —Б—В–≤–∞—А–∞ –Ї–∞–Њ —Д—Г–љ–Ї—Ж–Є—Ш–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Њ–±—Ш–µ–Ї—В–∞, —В—Ш. –Ї–∞–Њ —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–Є–љ–µ —Б–≤–µ—В–ї–Є—Е –Є —В–∞–Љ–љ–Є—Е –ї–Є–љ–Є—Ш–∞.
–Ф—А—Г–≥–Є–Љ —А–µ—З–Є–Љ–∞, –§–Ю–Я –Ї–Њ—А–Є—Б—В–Є –љ–µ —Ш–µ–і–∞–љ –Њ–±—Ш–µ–Ї—В, –љ–µ–≥–Њ –≤–µ—Ы–Є –±—А–Њ—Ш –Њ–±—Ш–µ–Ї–∞—В–∞ —А–∞–Ј–ї–Є—З–Є—В–Є—Е —И–Є—А–Є–љ–∞ –ї–Є–љ–Є—Ш–∞, –љ–∞ –Њ—Б–љ–Њ–≤—Г –Ї–Њ—Ш–Є—Е —Б–µ –і–Њ–ї–∞–Ј–Є –і–Њ –љ–µ–њ—А–µ–Ї–Є–і–љ–µ –ї–Є–љ–Є—Ш–µ (—В—Ш. –≥—А–∞—Д–Є–Ї–Њ–љa) –Ї–Њ—Ш–∞ –Њ–њ–Є—Б—Г—Ш–µ –Њ—И—В—А–Є–љ—Г —Б–ї–Є–Ї–µ —Г —А–∞—Б–њ–Њ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —Г –Ї–Њ–Љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А —Б—В–≤–∞—А–∞ –њ—А–µ–њ–Њ–Ј–љ–∞—В—Щ–Є–≤—Г —Б–ї–Є–Ї—Г.
–°–ї–Є–Ї–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞
–°–ї–Є–Ї—Г –§–Ю–Я –Њ–њ–Є—Б—Г—Ш–µ –љ–µ–Ї–Њ–ї–Є–Ї–Њ —З–Є–љ–Є–ї–∞—Ж–∞:
(1) –Њ–љ–∞ –Є—Б–Ї–∞–Ј—Г—Ш–µ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –≤–Є—Б–Є–љ—Г —Г —Б–ї–Є—Ж–Є —Б—В–≤–Њ—А–µ–љ—Г —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г,
(2) —В–∞–Ї–Њ—Т–µ –Є—Б–Ї–∞–Ј—Г—Ш–µ –±–Њ—З–љ–Є –њ–Њ–Љ–∞–Ї —Б–ї–Є–Ї–µ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ —Б–∞–≤—А—И–µ–љ–Є –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А,
(3) –Њ–љ–∞ —Ш–µ, –Ї–∞–Њ –Є —Б–∞–Љ–∞ –§–Ю–Я –Є —Ъ–µ–љ –Њ–±—Ш–µ–Ї—В, –Є–Ј—А–∞–ґ–µ–љ–∞ –љ–µ —Г –њ—А–Њ—Б—В–Њ—А–љ–Њ–Љ (—Б—В–≤–∞—А–љ–Њ–Љ) –і–Њ–Љ–µ–љ—Г, –љ–µ–≥–Њ —Г –і–Њ–Љ–µ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є (—Д—А–µ–Ї–≤–µ–љ—Ж–Є—Ш–µ),
(4) –Њ–љ–∞ —Ш–µ —Б—В–≤–Њ—А–µ–љ–∞ —Г –љ–µ–Ї–Њ—Е–µ—А–µ–љ—В–љ–Њ—Ш —Б–≤–µ—В–ї–Њ—Б—В–Є, –Є
(5) –Њ–љ–∞ —Ш–µ –Њ–њ—И—В–µ –Љ–µ—А–Є–ї–Њ –Ї–∞–Ї–≤–Њ—Ы–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ
–Т–Є—Б–Є–љ–∞ –Є –њ–Њ–Љ–∞–Ї —Б–Є–≥–љ–∞–ї–∞
![]() –°–Ы–Ш–Ъ–Р 1: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –Ч–Р –И–Х–Ф–Э–£ –£–І–Х–°–Ґ–Р–Э–Ю–°–Ґ
–°–Ы–Ш–Ъ–Р 1: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –Ч–Р –И–Х–Ф–Э–£ –£–І–Х–°–Ґ–Р–Э–Ю–°–Ґ
–£ –љ–∞—Ш—Ш–µ–і–љ–Њ—Б—В–∞–≤–љ—Ш–µ–Љ –Њ–±–ї–Є–Ї—Г, –§–Ю–Я —Б–µ –Љ–Њ–ґ–µ –њ—А–µ–і—Б—В–∞–≤–Є—В–Є –Ї–∞–Њ –≤–Є—Б–Є–љ–∞ —Б–Є–≥–љ–∞–ї–∞ –Є –њ–Њ–ї–Њ–ґ–∞—Ш–∞ –Њ–≤–µ —Б–ї–Є–Ї–µ —Г –і–∞—В–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –љ–∞ –Є—Б—В–µ —Г —Б–ї–Є—Ж–Є —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г, —Г —А–∞—Б–њ–Њ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —Б–Є–≥–љ–∞–ї–∞ –Њ–і –±–µ—Б–Ї—А–∞—Ш–љ–Њ —И–Є—А–Њ–Ї–Њ–≥ –і–Њ —И–Є—А–Є–љ–µ –љ–∞ –љ–Є–≤–Њ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —А–µ–Ј–∞, –љ–∞ –Ї–Њ—Ш–Њ—Ш –Ї–Њ–љ—В—А–∞—Б—В —Б–ї–Є–Ї–µ –њ–∞–і–∞ –љ–∞ –љ—Г–ї—Г, —В—Ш. —Б–Є–љ—Г—Б–Њ–Є–і –њ–Њ—Б—В–∞—Ш–µ –њ—А–∞–≤–∞ –ї–Є–љ–Є—Ш–∞. –Ю–≤–∞–Ї–Њ –Є–Ј—А–∞–ґ–µ–љ–∞ –≤–Є—Б–Є–љ–∞ —Б–Є–≥–љ–∞–ї–∞ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –≤–Є—Б–Є–љ—Г, –Є–ї–Є –≤–µ–ї–Є—З–Є–љ—Г –§–Ю–Я. –С–Њ—З–љ–Є –њ–Њ–Љ–∞–Ї —Б–ї–Є–Ї–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ —Ъ–µ–љ—Г —Д–∞–Ј—Г.
–°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ–Њ–Ї–∞–Ј—Г—Ш–µ –µ–ї–µ–Љ–µ–љ—В–µ –§–Ю–Я –Ј–∞ —Ш–µ–і–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В; —Ш–∞—Б–љ–Њ—Ы–µ —А–∞–і–Є, —Б–ї–Є–Ї–∞ –Є–Љ–∞ —Ш–µ–і–Є–љ–Є—З–љ–Њ —Г–≤–µ—Ы–∞—Ъ–µ (–±–Є—В–љ–Њ —Ш–µ –љ–∞–≥–ї–∞—Б–Є—В–Є –і–∞ –≤–Є—Б–Є–љ–∞ - –Т1/–Т2 - –Є —Д–∞–Ј–љ–Є –њ–Њ–Љ–∞–Ї ќФ —Б–Є–≥–љ–∞–ї–∞ –љ–Є—Б—Г –Ј–±–Є—А, –љ–µ–≥–Њ –і–≤–∞ –Ї–Њ–Љ–њ–ї–µ–Љ–µ–љ—В–∞—А–љ–∞ —Б–≤–Њ—Ш—Б—В–≤–∞ –§–Ю–Я –Ї–Њ—Ш–∞ –і–∞—Ш—Г –њ—Г–љ–Є –Њ–њ–Є—Б —Б–ї–Є–Ї–µ).
–Ф—А—Г–≥–Є–Љ —А–µ—З–Є–Љ–∞, –§–Ю–Я –Є–Ј—А–∞–ґ–∞–≤–∞ –Њ–≤–∞ –і–≤–∞ —Б–≤–Њ—Ш—Б—В–≤–∞ —Б–ї–Є–Ї–µ —Г —А–∞—Б–њ–Њ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —Б–Є–љ—Г—Б–Њ–Є–і–∞ –Њ–і –±–µ—Б–Ї–Њ–љ–∞—З–љ–Њ —И–Є—А–Њ–Ї–Є—Е –ї–Є–љ–Є—Ш–∞, –Ј–∞ –Ї–Њ—Ш–µ —Ш–µ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Г–≤–µ–Ї –њ–Њ—В–њ—Г–љ (—Ш–µ–і–∞–љ), –і–Њ —И–Є—А–Є–љ–µ –ї–Є–љ–Є—Ш–∞ –њ—А–Є –Ї–Њ—Ш–Њ—Ш –≤–Є—Б–Є–љa —Б–Є–љ—Г—Б–Њ–Є–і–∞ —Б–ї–Є–Ї–µ –њ–∞–і–∞ –љ–∞ –љ—Г–ї—Г, —В—Ш. –ї–Є–љ–Є—Ш–µ —Б–µ –≥—Г–±–µ –Є —Б–ї–Є–Ї–∞ –њ–Њ—Б—В–∞—Ш–µ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –Њ–±–∞—Б—Ш–∞–љ–∞ –њ–Њ–≤—А—И–Є–љ–∞.
–Т–Є—Б–Є–љ–∞ —Б–Є–≥–љ–∞–ї–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –Є—Б—В—Г —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ—В–≤–Њ—А—Г —Ш–µ –љ–∞—Ш–±–Є—В–љ–Є—Ш–µ —Б–≤–Њ—Ш—Б—В–≤–Њ —Б–ї–Є–Ї–µ, —Ш–µ—А –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –Љ–µ—А—Г —Ъ–µ–љ–µ –Њ—И—В—А–Є–љ–µ, —Б–∞–≥–ї–∞—Б–љ–Њ —Ш–µ–і–љ–Њ—Б—В–∞–≤–љ–Њ–Љ –Є–Ј—А–∞–Ј—Г:
- –Ъ=(–Т–≤-–Т–і)/(–Т–≤+–Т–і) ........ (1)
–≥–і–µ —Ш–µ –Ъ –Ї–Њ–љ—В—А–∞—Б—В (–Њ—И—В—А–Є–љ–∞) —Б–ї–Є–Ї–µ, –Т–≤ –≤–Є—Б–Є–љ–∞ (–∞–Љ–њ–ї–Є—В—Г–і–∞) –≤—А—Е–∞, –Є –Т–і –≤–Є—Б–Є–љ–∞ –і–љ–∞ —Б–Є–≥–љ–∞–ї–∞ (–≤–Є—Б–Є–љ–∞ –≤—А—Е–∞ —Ш–µ —Ш–µ–і–Є–љ–Є—З–љ–∞ –≤—А–µ–і–љ–Њ—Б—В, –∞ –≤–Є—Б–Є–љ–∞ –і–љ–∞ —Ш–µ –Є–Ј—А–∞–ґ–µ–љ–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ —Ъ—Г).
–£ —Б–Љ–Є—Б–ї—Г —Б—В–≤–∞—А–љ–Є—Е –Њ–±—Ш–µ–Ї–∞—В–∞, –њ–Њ—И—В–Њ —Ш–µ –≤–Є—Б–Є–љ–∞ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ —Б–Є–≥–љ–∞–ї–∞ –Љ–µ—А–∞ –Њ—И—В—А–Є–љ–µ (–Ї–Њ–љ—В—А–∞—Б—В–∞) —Б–ї–Є–Ї–µ, –§–Ю–Я –і–∞—Ш–µ –Љ–µ—А—Г –Ї–∞–Ї–≤–Њ—Ы–µ —Б–ї–Є–Ї–µ —Г —А–∞—Б–њ–Њ–љ—Г –Њ–і –љ–∞—Ш–≤–µ—Ы–Є—Е –Њ–±—Ш–µ–Ї–∞—В–∞ –і–Њ –Њ–±—Ш–µ–Ї–∞—В–∞ –љ–∞ –≥—А–∞–љ–Є—Ж–Є —А–∞–Ј–і–≤–Њ—Ш–љ–µ –Љ–Њ—Ы–Є. –Р–Ї–Њ –§–Ю–Я –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞ –њ–∞–і–∞ –љ–∞ –љ—Г–ї—Г –њ—А–µ –§–Ю–Я —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, –Њ–љ–∞ —В–∞–Ї–Њ—Т–µ —Г—Б—В–∞–љ–Њ–≤—Щ–∞–≤–∞ –љ–Њ–≤–Є, –љ–Є–ґ–Є –љ–Є–≤–Њ —А–∞–Ј–і–≤–Њ—Ш–љ–µ –Љ–Њ—Ы–Є –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞.
–Я–Њ—И—В–Њ –ї–Є–љ–Є—Ш–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞—Ш—Г —Б–Є–љ—Г—Б–Њ–Є–і–љ–Є —А–∞—Б–њ–Њ—А–µ–і –Ј—А–∞—З–µ—Ъ–∞, –њ–Њ–Љ–∞–Ї –ї–Є–љ–Є—Ш–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ —Б–ї–Є–Ї—Г —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г - –Ї–Њ—Ш–∞ —Б–µ —Г –Њ–≤–Њ–Љ –њ–Њ–≥–ї–µ–і—Г –њ–Њ–Ї–ї–∞–њ–∞ —Б–∞ –У–∞—Г—Б–Њ–≤—Б–Ї–Њ–Љ —Б–ї–Є–Ї–Њ–Љ - –њ—А–µ–і—Б—В–∞–≤—Щ–∞ —Д–∞–Ј—Г –§–Ю–Я. –Ъ–∞–і–∞ —Б–µ –Њ–≤–∞ —Д–∞–Ј–∞ —А–∞–Ј–ї–Є–Ї—Г—Ш–µ –Њ–і –љ—Г–ї–µ, –њ–Њ—Б—В–Њ—Ш–Є –±–Њ—З–љ–Є –њ–Њ–Љ–∞–Ї —Д–Є–Ј–Є—З–Ї–µ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –У–∞—Г—Б–Њ–≤—Б–Ї—Г —Б–ї–Є–Ї—Г –љ–Њ—А–Љ–∞–ї–∞–љ –љ–∞ —Б–Љ–µ—А –њ—А—Г–ґ–∞—Ъ–∞ –ї–Є–љ–Є—Ш–∞. –Ч–∞ —Б—А–∞–Ј–Љ–µ—А–љ–Њ –Љ–∞–ї–∞ –Є–Ј–Њ–±–ї–Є—З–µ—Ъ–∞ –§–®–Ґ, —Д–∞–Ј–љ–Є –і–µ–Њ —Д—Г–љ–Ї—Ж–Є—Ш–µ —Ш–µ –Є–ї–Є –љ—Г–ї–∞, –Є–ї–Є –Ј–∞–љ–µ–Љ–∞—А—Щ–Є–≤–Њ –Љ–∞–ї–Є, –Є –§–Ю–Я —Ш–µ —Г –њ–Њ—В–њ—Г–љ–Њ—Б—В–Є –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ–∞ —Ъ–µ–љ–Є–Љ –і–µ–ї–Њ–Љ –Ї–Њ—Ш–Є –Є–Ј—А–∞–ґ–∞–≤–∞ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞.
–Ф–Њ–Љ–µ–љ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є
–Ь–∞–і–∞ —Ш–µ –Ј–∞—Б–љ–Њ–≤–∞–љ–∞ –љ–∞ —Б–≤–Њ—Ш—Б—В–≤–Є–Љ–∞ —Д–Є–Ј–Є—З–Ї–µ, –Є–ї–Є –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–µ —Б–ї–Є–Ї–µ –Њ–±—Ш–µ–Ї—В–∞-—Б–Є–љ—Г—Б–Њ–Є–і–∞, –Ї–Њ—Ш–Є —Б–µ —Б—В–≤–∞—А–∞ –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–Њ–Љ (–Ј–±–Є—А–∞—Ъ–µ–Љ) —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ (–§–®–Ґ) –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞ —Б–∞ —Ш–µ–і–љ–µ, –Є –У–∞—Г—Б–Њ–≤—Б–Ї–µ (–≥–µ–Њ–Љ–µ—В—А–Є—Ш—Б–Ї–µ) —Б–ї–Є–Ї–µ –Њ–±—Ш–µ–Ї—В–∞ —Б–∞ –і—А—Г–≥–µ —Б—В—А–∞–љ–µ, –§–Ю–Я –љ–µ –Ї–Њ—А–Є—Б—В–Є –љ–µ–њ–Њ—Б—А–µ–і–љ–Њ —Д–Є–Ј–Є—З–Ї–∞ —Б–≤–Њ—Ш—Б—В–≤–∞ –Њ–±—Ш–µ–Ї—В–∞ –Є —Б–ї–Є–Ї–µ, –љ–µ–≥–Њ —Ъ–Є—Е–Њ–≤ –Њ–±–ї–Є–Ї —Г –і–Њ–Љ–µ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є (—Д—А–µ–Ї–≤–µ–љ—Ж–Є—Ш–µ), —В–Ј–≤. —Б–њ–µ–Ї—В—А—Г–Љ (—Г–Њ–њ—И—В–µ–љ–Њ, –љ–Є–Ј —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Ї–Њ—Ш–µ –Ї–Њ–Љ–±–Є–љ–Њ–≤–∞–љ–µ —Г –§—Г—А–Є—Ш–µ–Њ–≤–Њ—Ш —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–Є –њ—А–Њ–Є–Ј–≤–Њ–і–µ –Њ–і—А–µ—Т–µ–љ—Г –ї–Є–љ–Є—Ш—Г –Є–ї–Є –Њ–±–ї–Є–Ї). –Ч–∞ —Б–Є–љ—Г—Б–Њ–Є–і, –љ–∞ –њ—А–Є–Љ–µ—А, —Б–њ–µ–Ї—В—А—Г–Љ —Б–µ —Б–∞—Б—В–Њ—Ш–Є –Њ–і —Б–∞–Љ–Њ —Ш–µ–і–љ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, –і–µ—Д–Є–љ–Є—Б–∞–љ–µ –њ–µ—А–Є–Њ–і–Њ–Љ –Є –≤–Є—Б–Є–љ–Њ–Љ (–∞–Љ–њ–ї–Є—В—Г–і–Њ–Љ), –Ї–Њ—Ш–∞ —Ш–µ, –љ–∞—А–∞–≤–љ–Њ, —Г—З–µ—Б—В–∞–ї–Њ—Б—В —Б–∞–Љ–Њ–≥ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ —Б–Є–≥–љ–∞–ї–∞.
–Э–µ–Ї–Њ—Е–µ—А–µ–љ—В–љ–∞ —Б–≤–µ—В–ї–Њ—Б—В
–І–Є—Ъ–µ–љ–Є—Ж–∞ –і–∞ –§–Ю–Я –Њ–њ–Є—Б—Г—Ш–µ —Б–≤–Њ—Ш—Б—В–≤–∞ —Б–ї–Є–Ї–µ —Б—В–≤–Њ—А–µ–љ–µ –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–Њ–Љ –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ –Њ–±—Ш–µ–Ї—В–∞ –Є –§–®–Ґ, —В—Ш. –µ–љ–µ—А–≥–Є—Ш–µ —Б–ї–Є–Ї–µ —В–∞—З–Ї–µ –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞, –≥–Њ–≤–Њ—А–Є –і–∞ –§–Ю–Я –≤–∞–ґ–Є –Ј–∞ –љ–µ–Ї–Њ—Е–µ—А–µ–љ—В–љ—Г —Б–≤–µ—В–ї–Њ—Б—В, —В–µ —Б–µ –њ—Г–љ–Є–Љ –Є–Љ–µ–љ–Њ–Љ –Љ–Њ–ґ–µ –Ј–≤–∞—В–Є –љ–µ–Ї–Њ—Е–µ—А–µ–љ—В–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ (–Њ–њ—В–Є—З–Ї–∞ —Б–ї–Є–Ї–∞ —Г –Ї–Њ—Е–µ—А–µ–љ—В–љ–Њ—Ш —Б–≤–µ—В–ї–Њ—Б—В–Є —Ш–µ –і–µ—Д–Є–љ–Є—Б–∞–љ–∞ –Ї–∞–Њ –Ї–≤–∞–і—А–∞—В –Ј–±–Є—А–љ–µ –∞–Љ–њ–ї–Є—В—Г–і–µ —Г —Б–ї–Є—Ж–Є, –∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Ї–Њ—Ш–∞ –Њ–њ–Є—Б—Г—Ш–µ –∞–Љ–њ–ї–Є—В—Г–і—Г —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞ —Г –Ї–Њ—Е–µ—А–µ–љ—В–љ–Њ—Ш —Б–≤–µ—В–ї–Њ—Б—В–Є –Ј–Њ–≤–µ —Б–µ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Ї–Њ—Е–µ—А–µ–љ—В–љ–Њ–≥ –њ—А–µ–љ–Њ—Б–∞).
–Ь–µ—А–Є–ї–Њ –Ї–∞–Ї–≤–Њ—Ы–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ
–Ш–Ј–Њ–±–ї–Є—З–µ—Ъ–∞ –§–®–Ґ –Ј–±–Њ–≥ –Њ–њ—В–Є—З–Ї–Є—Е –∞–±–µ—А–∞—Ж–Є—Ш–∞, –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –∞–Љ–њ–ї–Є—В—Г–і–µ —Б–≤–µ—В–ї–Њ—Б–љ–Є—Е —В–∞–ї–∞—Б–∞ –Ї—А–Њ–Ј –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А - –≥–і–µ —Б—Г –љ–∞—Ш—З–µ—И—Ы–Є —Б–ї—Г—З–∞—Ш –Ј–∞–Ї–ї–Њ–љ–Є —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г - –Є –і—А—Г–≥–Є—Е —З–Є–љ–Є–ї–∞—Ж–∞, —Г—В–Є—З—Г –љ–∞ –Ї–∞–Ї–≤–Њ—Ы—Г –Њ–≤–µ –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–µ —Б–ї–Є–Ї–µ. –£ –љ–∞—З–µ–ї—Г, –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–∞ –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ –Њ–±—Ш–µ–Ї—В–∞ –Є –§–®–Ґ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —Г–Ј—А–Њ–Ї—Г—Ш–µ —И–Є—А–µ—Ъ–µ –µ–љ–µ—А–≥–Є—Ш–µ –Є–Ј —Б—Ш–∞—Ш–љ–Є—Е —Г —В–∞–Љ–љ–µ –ї–Є–љ–Є—Ш–µ, —Б–љ–Є–ґ–∞–≤–∞—Ш—Г—Ы–Є –Њ—И—В—А–Є–љ—Г –љ–∞—Б—В–∞–ї–µ —Д–Є–Ј–Є—З–Ї–µ —Б–ї–Є–Ї–µ –Є —Ъ–µ–љ—Г —А–∞–Ј–і–≤–Њ—Ш–љ—Г –Љ–Њ—Ы, —З–∞–Ї –Є —Г —Б–ї—Г—З–∞—Ш—Г —В–Ј–≤. —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –®—В–Њ —Ш–µ –µ–љ–µ—А–≥–Є—Ш–∞ –§–®–Ґ –≤–Є—И–µ —А–∞—И–Є—А–µ–љ–∞ –∞–±–µ—А–∞—Ж–Є—Ш–∞–Љ–∞ –Є –і—А—Г–≥–Є–Љ —З–Є–љ–Є–Њ—Ж–Є–Љ–∞ —Б–∞ —Б–ї–Є—З–љ–Є–Љ –µ—Д–µ–Ї—В–Њ–Љ, —В–Њ —Б—Г –≤–µ—Ы–µ –Є –љ–µ–≥–∞—В–Є–≤–∞–љ–µ –њ–Њ—Б–ї–µ–і–Є—Ж–µ –њ–Њ –Ї–∞–Ї–≤–Њ—Ы—Г —Б–ї–Є–Ї–µ.
–У—А–∞—Д–Є–Ї–Њ–љ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞
–£—Б–њ—А–∞–≤–љ–∞ —Б–Ї–∞–ї–∞ –§–Ю–Я –≥—А–∞—Д–Є–Ї–Њ–љ–∞ —Ш–µ –Ј–∞ –≤–Є—Б–Є–љ—Г —Б–Є–≥–љ–∞–ї–∞ - —В—Ш. –Ј–∞ –∞–Љ–њ–ї–Є—В—Г–і—Г —Б–Є–љ—Г—Б–Њ–Є–і–∞ –µ–љ–µ—А–≥–Є—Ш–µ –Ј—А–∞—З–µ—Ъ–∞ –Ї–Њ—Ш–Є –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –Њ–±—Ш–µ–Ї—В –§–Ю–Я - –і–Њ–Ї —Ш–µ –≤–Њ–і–Њ—А–∞–≤–љ–∞ —Б–Ї–∞–ї–∞ –Ј–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В (—Д—А–µ–Ї–≤–µ–љ—Ж–Є—Ш—Г) –Њ–≤–Њ–≥ —Б–Є–љ—Г—Б–Њ–Є–і–∞.
–°–Ї–∞–ї–∞ –≤–Є—Б–Є–љ–µ —Ш–µ –і–∞—В–∞ –Њ–і –љ—Г–ї–µ –і–Њ —Ш–µ–і–∞–љ, —В—Ш. –Њ–і –љ–Є–≤–Њ–∞ –љ–∞ –Ї–Њ–Љ —Б–µ —Б–ї–Є–Ї–∞ –њ–Њ—В–њ—Г–љ–Њ –≥—Г–±–Є, –њ–Њ—Б—В–∞—Ш—Г—Ы–Є —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –Њ—Б–≤–µ—В—Щ–µ–љ–∞ –њ–Њ–≤—А—И–Є–љ–∞, –і–Њ –љ–Њ–≤–Њ–∞ –љ–∞ –Ї–Њ–Љ —Ш–µ –≤–Є—Б–Є–љ–∞ (–µ–љ–≥. modulus) —Б–Є–≥–љ–∞–ї–∞ —Ш–µ–і–љ–∞–Ї–∞ –≤–Є—Б–Є–љ–Є —Г —Б–ї–Є—Ж–Є —Б—В–≤–Њ—А–µ–љ–Њ—Ш —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г.
–°–Ї–∞–ї–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —Б–Є–≥–љ–∞–ї–∞, –Ї–Њ—Ш–∞ —Б–µ –њ–Њ –њ—А–∞–≤–Є–ї—Г –Њ–±–µ–ї–µ–ґ–∞–≤–∞ —Б–ї–Њ–≤–Њ–Љ –≥—А—З–Ї–Њ–≥ –∞–ї—Д–∞–±–µ—В–∞ ќљ (–љ–Є), —Ш–µ –Њ–±–Є—З–љ–Њ —В–∞–Ї–Њ—Т–µ –і–∞—В–∞ –Њ–і 0 –і–Њ 1, –Ї–∞–Њ –±—А–Њ—Ш –Њ–±—А–љ—Г—В–Њ —Б—А–∞–Ј–Љ–µ—А–∞–љ –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–Њ—Ш —А–∞–Ј–і–≤–Њ—Ш–љ–Њ—Ш –Љ–Њ—Ы–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ (ќї/D –Ј–∞ —Б–∞–≤—А—И–µ–љ –Ї—А—Г–ґ–љ–Є –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А, –≥–і–µ —Ш–µ ќї —В–∞–ї–∞—Б–љ–∞ –і—Г–ґ–Є–љ–∞ —Б–≤–µ—В–ї–Њ—Б—В–Є, –∞ D –њ—А–µ—З–љ–Є–Ї –Њ—В–≤–Њ—А–∞). –Ф—А—Г–≥–Є–Љ —А–µ—З–Є–Љ–∞, –≤–Њ–і–Њ—А–∞–≤–љ–∞ —Б–Ї–∞–ї–∞ —Б–µ –Ї—А–µ—Ы–µ –Њ–і 0 –Ј–∞ –±–µ—Б–Ї–Њ–љ–∞—З–љ–Њ —И–Є—А–Њ–Ї —Б–Є–љ—Г—Б–Њ–Є–і (—В—Ш. –±–µ—Б–Ї–Њ–љ–∞—З–љ–Њ —И–Є—А–Њ–Ї–µ —Б–≤–µ—В–ї–µ –Є —В–∞–Љ–љ–µ –ї–Є–љ–Є—Ш–µ –Њ–±—Ш–µ–Ї—В–∞) –і–Њ 1 –Ј–∞ —И–Є—А–Є–љ—Г –ї–Є–љ–Є—Ш–∞ - –≥–і–µ —Ш–µ —И–Є—А–Є–љ–∞ –ї–Є–љ–Є—Ш–µ —А–∞–Ј–Љ–∞–Ї –Є–Ј–Љ–µ—Т—Г –і–≤–µ —В–∞—З–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞ —Г –Є—Б—В–Њ—Ш —Д–∞–Ј–Є, —В—Ш. —Ш–µ–і–љ–∞–Ї–∞ —И–Є—А–Є–љ–Є —Б–≤–µ—В–ї–µ –Є —В–∞–Љ–љ–µ –ї–Є–љ–Є—Ш–µ –Ј–∞—Ш–µ–і–љ–Њ - —Ш–µ–і–љ–∞–Ї—Г D/ќї, –≥—А–∞–љ–Є—З–љ–Њ—Ш —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞.
–Т–Њ–і–Њ—А–∞–≤–љ–∞ —Б–Ї–∞–ї–∞ —Б–µ —В–∞–Ї–Њ—Т–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –Є –ї–Є–љ–µ–∞—А–љ–Њ, –Ї–∞–Њ 1/(ќї/D)∆Т=1/ќїF –Ї–∞–і, –Ј–∞ —В–∞–ї–∞—Б–љ—Г –і—Г–ґ–Є–љ—Г ќї —Г –Љ–Є–ї–Є–Љ–µ—В—А–Є–Љ–∞, –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –±—А–Њ—Ш –ї–Є–љ–Є—Ш–∞ –њ–Њ –Љ–Є–ї–Є–Љ–µ—В—А—Г (∆Т —Ш–µ –ґ–Є–ґ–љ–∞ –і–∞—Щ–Є–љ–∞, –∞ F —Д–Њ–Ї–∞–ї–љ–Є —А–∞—Ж–Є–Њ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞).
–Ч–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А, –≤–Є—Б–Є–љa —Б–Є–≥–љ–∞–ї–∞, —В—Ш. –Њ—И—В—А–Є–љ–∞ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ –Њ–±—Ш–µ–Ї—В–∞, —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –Њ–њ–∞–і–∞ –Њ–і 1 –Ј–∞ –±–µ—Б–Ї–Њ–љ–∞—З–љ–Њ —И–Є—А–Њ–Ї–µ –ї–Є–љ–Є—Ш–µ (—В—Ш. –Ј–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В —Б–Є–≥–љ–∞–ї–∞ —Ш–µ–і–љ–∞–Ї—Г –љ—Г–ї–Є) –і–Њ –љ—Г–ї–µ –Ј–∞ —И–Є—А–Є–љ—Г –ї–Є–љ–Є—Ш–∞ –њ—А–Є –Ї–Њ—Ш–Њ—Ш —Ш–µ —А–∞–Ј–Љ–∞–Ї –Є–Ј–Љ–µ—Т—Г —Б—А–µ–і–Є—И—В–∞ –і–≤–µ —Б—Г—Б–µ–і–љ–µ —Б–≤–µ—В–ї–µ –ї–Є–љ–Є—Ш–µ —Ш–µ–і–љ–∞–Ї ќї/D. –Ш–Ј—А–∞–ґ–µ–љ–∞ —Ш–µ —Ш–µ–і–љ–Њ—Б—В–∞–≤–љ–Њ –Ї–∞–Њ:
- –§–Ю–Я(ќљ)=(2/ѕА)[cos-1ќљ-ќљ(1-ќљ2)0.5] ........ (2)
–≥–і–µ —Ш–µ —Г–≥–∞–Њ –і–Њ–±–Є—Ш–µ–љ –Є–Ј cos-1ќљ=–∞rccos(ќљ) –Є–Ј—А–∞–ґ–µ–љ —Г —А–∞–і–Є—Ш–∞–љ–Є–Љ–∞ (—В—Ш. –і–µ–ї–Є —Б–µ —Б–∞ 180/ѕА). –Ш–Ј—А–∞–Ј–Є
- –§–Ю–Я = (ќ±/90)-2ќљsinќ±/ѕА = (ќ±/90)-sin(2ќ±)/ѕА ........ (2.1)
–≥–і–µ —Ш–µ cosќ±=ќљ, —В—Ш. ќ±=arccos(ќљ), –і–∞—Ш—Г –Є—Б—В–Є —А–µ–Ј—Г–ї—В–∞—В.
–У—А–∞–љ–Є—З–љ–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В –њ—А–Є –Ї–Њ—Ш–Њ—Ш —Б–µ –ї–Є–љ–Є—Ш–µ –≥—Г–±–µ –љ–∞–Ј–Є–≤–∞ —Б–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В —А–µ–Ј–∞ (–µ–љ–≥. cutoff frequency). –Ч–∞ –Ј–љ–∞—В–љ–∞ –Є–Ј–Њ–±–ї–Є—З–µ—Ъ–∞ —Б–ї–Є–Ї–µ —В–∞—З–Ї–µ —Г –Њ–њ—В–Є—З–Ї–Њ–Љ —Б–Ї–ї–Њ–њ—Г, —Г—З–µ—Б—В–∞–ї–Њ—Б—В —А–µ–Ј–∞ —Б–µ —Б–Љ–∞—Ъ—Г—Ш–µ, —В—Ш. –њ–Њ–Љ–µ—А–∞ —Б–µ –Ї–∞ —И–Є—А–Є–Љ –ї–Є–љ–Є—Ш–∞–Љ–∞.
 –°–Ы–Ш–Ъ–Р 2: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –Ч–Р –°–Р–Т–†–®–Х–Э –Ш –Ч–Р –Э–Х–°–Р–Т–†–®–Х–Э –Ю–Я–Ґ–Ш–І–Ъ–Ш –Ю–Ґ–Т–Ю–†
–°–Ы–Ш–Ъ–Р 2: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –Ч–Р –°–Р–Т–†–®–Х–Э –Ш –Ч–Р –Э–Х–°–Р–Т–†–®–Х–Э –Ю–Я–Ґ–Ш–І–Ъ–Ш –Ю–Ґ–Т–Ю–† –Ы–Є–љ–Є—Ш–∞ –Њ–њ–∞–і–∞—Ъ–∞ –Њ—И—В—А–Є–љ–µ —Б–ї–Є–Ї–µ, —В—Ш. –§–Ю–Я –≥—А–∞—Д, —Г –њ—А–Є—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞ —Г–≤–µ–Ї —Ш–µ –љ–Є–ґ–∞ –Њ–і –Є—Б—В–µ –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А. –Ш—Б—В–Њ –≤–∞–ґ–Є –Ј–∞ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А —Б–∞ –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Є–Љ –њ—А–µ–љ–Њ—Б–Њ–Љ –∞–Љ–њ–ї–Є—В—Г–і–µ —В–∞–ї–∞—Б–∞, —Б–∞ –Є–Ј—Г–Ј–µ—В–Ї–Њ–Љ –њ—А—Б—В–µ–љ–∞—Б—В–Њ–≥ (–∞–љ—Г–ї–∞—А–љ–Њ–≥) –Њ—В–≤–Њ—А–∞, —Г –Ї–Њ–Љ —Б–ї—Г—З–∞—Ш—Г —Ш–µ –Њ–њ—В–Є—З–Ї–Є –њ—А–µ–љ–Њ—Б –±–Њ—Щ–Є –љ–µ–≥–Њ —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ—В–≤–Њ—А—Г –Ј–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Њ–і –Њ–Ї–Њ 0.5 (–Ј–∞–≤–Є—Б–Є –Њ–і –≤–µ–ї–Є—З–Є–љ–µ —Б—А–µ–і–Є—И—Ъ–µ–≥ –Ј–∞–Ї–ї–Њ–љ–∞) –Є –≤–Є—И–µ.
–Э–∞ —Б–ї–Є—Ж–Є –і–µ—Б–љ–Њ —Ш–µ –§–Ю–Я –Ї–∞–Ї–Њ —Ш–µ –Њ–±–Є—З–љ–Њ –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ–∞ (–љ–∞—Ш—З–µ—И—Ы–µ –Ї–∞–Њ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ, –§–Я–Т). –У—А–∞—Д –Њ—В–≤–Њ—А–∞ —Б–∞ –∞–±–µ—А–∞—Ж–Є—Ш–∞–Љ–∞ (—Ж—А–≤–µ–љ–∞ –ї–Є–љ–Є—Ш–∞) –Є—Б–Ї–∞–Ј—Г—Ш–µ –Ј–љ–∞—З–∞—Ш–∞–љ –њ–∞–і –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞, —В—Ш. –Њ—И—В—А–Є–љ–µ —Б–ї–Є–Ї–µ, –љ–∞—А–Њ—З–Є—В–Њ –Ј–∞ —И–Є—А–Є–љ–µ –ї–Є–љ–Є—Ш–∞ - –Є–ї–Є, —Г–Њ–њ—И—В–µ–љ–Њ, –Ј–∞ –њ—А–Њ—И–Є—А–µ–љ–µ –і–µ—В–∞—Щ–µ —В–µ –≤–µ–ї–Є—З–Є–љ–µ - –Њ–і –Њ–Ї–Њ 0,2 –і–Њ –Њ–Ї–Њ 0,8 D/ќї —Г—З–µ—Б—В–∞–ї–Њ—Б—В, –Є–ї–Є –Њ–і –Њ–Ї–Њ –њ–µ—В –њ—Г—В–∞ –і–Њ –Њ–Ї–Њ 1,25 –њ—Г—В–∞ –≤–µ—Ы–µ –Њ–і —И–Є—А–Є–љ–µ –ї–Є–љ–Є—Ш–∞ –њ—А–Є –Ї–Њ—Ш–Њ—Ш —Б–µ –Њ–љ–µ –њ–Њ—В–њ—Г–љ–Њ –≥—Г–±–µ (–≥—А–∞–љ–Є—З–љ–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В). –£ —Б–ї—Г—З–∞—Ш—Г –і–∞ –§–Ю–Я –њ–∞–і–љ–µ –љ–∞ –љ—Г–ї—Г –њ—А–µ –≥—А–∞–љ–Є—З–љ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, —А–∞—Х–і–≤–Њ—Ш–љ–∞ –Љ–Њ—Ы –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ —Ш–µ —В–∞–Ї–Њ—Т–µ –ї–Њ—И–Є—Ш–∞ –љ–µ–≥–Њ –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ—В–≤–Њ—А.
–£ –Њ–Ї–≤–Є—А—Г –≥–Њ—А–µ –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј–∞–љ–∞ —Ш–µ –≤–µ–Ј–∞ –Є–Ј–Љ–µ—Т—Г –≤–Є—Б–Є–љ–µ, —Г—З–µ—Б—В–∞–љ–Њ—Б—В–Є –Є —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Њ–≥ —Б–Є–≥–љ–∞–ї–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞.
–Ь–∞—В–µ–Љ–∞—В–Є—З–Ї–Є –Њ–±–ї–Є–Ї —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞
–§—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ —Б–µ –Љ–Њ–ґ–µ –Є–Ј—А–∞–Ј–Є—В–Є –љ–∞ —А–∞–Ј–ї–Є—З–Є—В–µ –љ–∞—З–Є–љ–µ, –∞–ї–Є —Г –Њ—Б–љ–Њ–≤–Є —Ш–µ –Є–Ј—А–∞–ґ–µ–љ–∞ –Є–ї–Є –Ї–∞–Њ –§—Г—А–Є—Ш–µ–Њ–≤–∞ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ, –Є–ї–Є –Ї–∞–Њ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –Ґ–∞–Ї–Њ—Т–µ, —Г —Г–Њ–њ—И—В–µ–љ–Њ–Љ –Њ–±–ї–Є–Ї—Г —Ъ–µ–љ–∞ –і–≤–∞ –Њ—Б–љ–Њ–≤–љ–∞ –і–µ–ї–∞, –Љ–Њ–ґ–µ —Б–µ –њ—А–µ–і—Б—В–∞–≤–Є—В–Є –Ї–∞–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–∞ –≤–Є—Б–Є–љ–∞, –Ї–Њ—Ш–∞ —Б–∞–і—А–ґ–Є –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ –Є —Д–∞–Ј–љ–Є –њ–Њ–Љ–∞–Ї –љ–∞ –њ—А–Њ–Є–Ј–≤–Њ—Щ–љ–Њ—Ш —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є.
–§—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ї–∞–Њ –§—Г—А–Є—Ш–µ–Њ–≤–∞ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ
–Ю–≤–Њ —Ш–µ –Њ—Б–љ–Њ–≤–љ–Є –Њ–±–ї–Є–Ї –§–Ю–Я. –Я–Њ —В–µ–Њ—А–Є—Ш–Є –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–µ, –§—Г—А–Є—Ш–µ–Њ–≤–∞ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–∞ –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–µ –і–≤–µ —Д—Г–љ–Ї—Ж–Є—Ш–µ —Ш–µ —Ш–µ–і–љ–∞–Ї–∞ –њ—А–Њ–Є–Ј–≤–Њ–і—Г –§—Г—А–Є—Ш–µ–Њ–≤–Є—Е —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–∞ –Њ–≤–Є—Е —Д—Г–љ–Ї—Ж–Є—Ш–∞. –Я–Њ—И—В–Њ —Ш–µ —Д–Є–Ј–Є—З–Ї–∞ –Њ–њ—В–Є—З–Ї–∞ —Б–ї–Є–Ї–∞ —Г –љ–µ–Ї–Њ—Е–µ—А–µ–љ—В–љ–Њ—Ш —Б–≤–µ—В–ї–Њ—Б—В–Є –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–∞ –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ –Є —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ (–µ–љ–≥. Point spread function, PSF), –§—Г—А–Є—Ш–µ–Њ–≤–∞ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–∞ —Б–ї–Є–Ї–µ - —В—Ш. —Ъ–µ–љ–Њ–Љ –ї–µ–њ–µ–Ј–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є - —Ш–µ –њ—А–Њ–Є–Ј–≤–Њ–і –§—Г—А–Є—Ш–µ–Њ–≤–µ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–µ –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ (–Ї–Њ—Ш–∞ —Ш–µ –Є—Б—В–∞ –Ї–∞–Њ –Њ–±—Ш–µ–Ї—В, –Є–Ј—Г–Ј–µ–≤ –Ј–∞ —З–Є–љ–Є–ї–∞—Ж —Г–≤–µ—Ы–∞—Ъ–∞) –Є –§—Г—А–Є—Ш–µ–Њ–≤–µ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—Ш–µ —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ, –і–∞–Ї–ї–µ –§–Ю–Я, –Ї–Њ—Ш–∞ —Ш–µ –Ї–Њ–ї–Є—З–љ–Є–Ї –≤–Є—Б–Є–љ–µ –Ї–Њ–љ—В—А–∞—Б—В–∞ (–µ–љ–≥. modulation) —Б–ї–Є–Ї–µ –Є –њ—А–µ–і–Љ–µ—В–∞ (—В—Ш. –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞). –Я—А–µ–Љ–∞ —В–Њ–Љ–µ, –§–Ю–Я —Ш–µ –і–∞—В–∞ —Б–∞:
![{\displaystyle FOP({\vec {\nu }}_{s})=\int _{0}^{1}PSF({\vec {r}}_{s})\,exp[2\pi i{\vec {\nu }}_{s}\cdot {\vec {r}}_{s}]d{\vec {r}}_{s}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e00e39b82e4d8f60430d7cef0d6c2da9e18dc609) ........ (3)
........ (3)
![{\displaystyle ={\frac {1}{E(\lambda R)^{2}}}\int _{0}^{1}\,d{\vec {r}}_{s}\,exp[2\pi i{\vec {\nu }}_{s}\cdot {\vec {r}}_{s}]\left|\int _{0}^{1}P({\vec {r}}_{o})exp[-{\frac {2\pi i}{\lambda R}}{\vec {r}}_{o}\cdot {\vec {r}}_{s}]d{\vec {r}}_{o}\right|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d6a34f3b465c3c3274b257c46d0f065cb85473c) ....... (3.1)
....... (3.1)
–≥–і–µ —Ш–µ  –≤–µ–Ї—В–Њ—А –њ—А–Њ—Б—В–Њ—А–љ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, –Њ–і—А–µ—Т–µ–љ —А–∞–Ј–Љ–∞–Ї–Њ–Љ v –Є–Ј–Љ–µ—Т—Г –і–≤–µ —Б—Г—Б–µ–і–љ–µ —В–∞—З–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞ —Г –Є—Б—В–Њ—Ш —Д–∞–Ј–Є, —В—Ш. —И–Є—А–Є–љ–Њ–Љ –ї–Є–љ–Є—Ш–∞ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞, –Є –Њ–±—А—В–љ–Є–Љ —Г–≥–ї–Њ–Љ ѕЖ (–Є–љ—В–µ–≥—А–∞—Ж–Є—Ш–∞ —Б–µ –Њ–±–∞–≤—Щ–∞ –Ј–∞ —Б–≤–µ –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш–µ —Б–ї–Є–Ї–µ —Г–љ—Г—В–∞—А 360 —Б—В–µ–њ–µ–љ–Є, —И—В–Њ —Ш–µ –Њ–і –Ј–љ–∞—З–∞—Ш–∞ —Ш–µ–і–Є–љ–Њ –∞–Ї–Њ —Д—Г–љ–Ї—Ж–Є—Ш–∞ —И–Є—А–µ—Ъ–∞ —А–∞—Б–њ–Њ–љ–∞ –љ–Є—Ш–µ –Њ–±—А—В–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–љ–∞), –∞
–≤–µ–Ї—В–Њ—А –њ—А–Њ—Б—В–Њ—А–љ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, –Њ–і—А–µ—Т–µ–љ —А–∞–Ј–Љ–∞–Ї–Њ–Љ v –Є–Ј–Љ–µ—Т—Г –і–≤–µ —Б—Г—Б–µ–і–љ–µ —В–∞—З–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞ —Г –Є—Б—В–Њ—Ш —Д–∞–Ј–Є, —В—Ш. —И–Є—А–Є–љ–Њ–Љ –ї–Є–љ–Є—Ш–∞ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞, –Є –Њ–±—А—В–љ–Є–Љ —Г–≥–ї–Њ–Љ ѕЖ (–Є–љ—В–µ–≥—А–∞—Ж–Є—Ш–∞ —Б–µ –Њ–±–∞–≤—Щ–∞ –Ј–∞ —Б–≤–µ –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш–µ —Б–ї–Є–Ї–µ —Г–љ—Г—В–∞—А 360 —Б—В–µ–њ–µ–љ–Є, —И—В–Њ —Ш–µ –Њ–і –Ј–љ–∞—З–∞—Ш–∞ —Ш–µ–і–Є–љ–Њ –∞–Ї–Њ —Д—Г–љ–Ї—Ж–Є—Ш–∞ —И–Є—А–µ—Ъ–∞ —А–∞—Б–њ–Њ–љ–∞ –љ–Є—Ш–µ –Њ–±—А—В–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–љ–∞), –∞  —Ш–µ –њ–Њ–Ј–Є—Ж–Є–Њ–љ–Є –≤–µ–Ї—В–Њ—А –Ї–Њ—Ш–Є —Б–њ–∞—Ш–∞ –Њ–њ—В–Є—З–Ї—Г –Њ—Б—Г —Б–∞ –њ—А–Њ–Є–Ј–≤–Њ—Щ–љ–Њ–Љ —В–∞—З–Ї–Њ–Љ —Г —А–∞–≤–љ–Є —Б–ї–Є–Ї–µ, –Њ–і—А–µ—Т–µ–љ —А–∞–Ј–Љ–∞–Ї–Њ–Љ r –Є–Ј–Љ–µ—Т—Г –Њ—Б–µ –Є —В–∞—З–Ї–µ, –Є —Г–≥–ї–Њ–Љ –Њ—В–≤–Њ—А–∞ ќ≥.
—Ш–µ –њ–Њ–Ј–Є—Ж–Є–Њ–љ–Є –≤–µ–Ї—В–Њ—А –Ї–Њ—Ш–Є —Б–њ–∞—Ш–∞ –Њ–њ—В–Є—З–Ї—Г –Њ—Б—Г —Б–∞ –њ—А–Њ–Є–Ј–≤–Њ—Щ–љ–Њ–Љ —В–∞—З–Ї–Њ–Љ —Г —А–∞–≤–љ–Є —Б–ї–Є–Ї–µ, –Њ–і—А–µ—Т–µ–љ —А–∞–Ј–Љ–∞–Ї–Њ–Љ r –Є–Ј–Љ–µ—Т—Г –Њ—Б–µ –Є —В–∞—З–Ї–µ, –Є —Г–≥–ї–Њ–Љ –Њ—В–≤–Њ—А–∞ ќ≥.
–Я—А–Њ–Є–Ј–≤–Њ–і –Њ–≤–Є—Е –≤–µ–Ї—В–Њ—А–∞ —Б–µ —В–∞–Ї–Њ—Т–µ –Љ–Њ–ґ–µ –Є–Ј—А–∞–Ј–Є—В–Є –Ї–∞–Њ –њ—А–Њ–Є–Ј–≤–Њ–і –∞–њ—Б–Њ–ї—Г—В–љ–Є—Е –≤—А–µ–і–љ–Њ—Б—В–Є (–і—Г–ґ–Є–љ–∞) –≤–µ–Ї—В–Њ—А–∞ –Є —Ъ–Є—Е–Њ–≤–Њ–≥ –Љ–µ—Т—Г—Б–Њ–±–љ–Њ–≥ —Г–≥–ї–∞; —Г –Њ–≤–Њ–Љ —Б–ї—Г—З–∞—Ш—Г,  =vrcos(ѕЖ-ќ≥). –†–∞–Ј–ї–Њ–Љ–∞–Ї –њ—А–µ–і –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ —Г (3.1) —Ш–µ —З–Є–љ–Є–ї–∞—Ж –Ї–Њ—Ш–Є —Б–≤–Њ–і–Є —Б—А–µ–і–Є—И—Ъ—Г –≤–Є—Б–Є–љ—Г –§–Ю–Я –љ–∞ —Ш–µ–і–Є–љ–Є—З–љ—Г –≤—А–µ–і–љ–Њ—Б—В —Г –Њ–і—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞ (–Х —Ш–µ —Г–Ї—Г–њ–љ–∞ –µ–љ–µ—А–≥–Є—Ш–∞ —Г —А–∞–≤–љ–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, R —Ш–µ –њ–Њ–ї—Г–њ—А–µ—З–љ–Є–Ї –Ј–∞–Ї—А–Є–≤—Щ–µ–љ–Њ—Б—В–Є —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞, P —Ш–µ —Б–≤–µ–і–µ–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, –Є ќї —Ш–µ —В–∞–ї–∞—Б–љ–∞ –і—Г–ґ–Є–љ–∞).
=vrcos(ѕЖ-ќ≥). –†–∞–Ј–ї–Њ–Љ–∞–Ї –њ—А–µ–і –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ —Г (3.1) —Ш–µ —З–Є–љ–Є–ї–∞—Ж –Ї–Њ—Ш–Є —Б–≤–Њ–і–Є —Б—А–µ–і–Є—И—Ъ—Г –≤–Є—Б–Є–љ—Г –§–Ю–Я –љ–∞ —Ш–µ–і–Є–љ–Є—З–љ—Г –≤—А–µ–і–љ–Њ—Б—В —Г –Њ–і—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞ (–Х —Ш–µ —Г–Ї—Г–њ–љ–∞ –µ–љ–µ—А–≥–Є—Ш–∞ —Г —А–∞–≤–љ–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, R —Ш–µ –њ–Њ–ї—Г–њ—А–µ—З–љ–Є–Ї –Ј–∞–Ї—А–Є–≤—Щ–µ–љ–Њ—Б—В–Є —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞, P —Ш–µ —Б–≤–µ–і–µ–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, –Є ќї —Ш–µ —В–∞–ї–∞—Б–љ–∞ –і—Г–ґ–Є–љ–∞).
–§—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ї–∞–Њ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞
–Ш–Ј –њ—А–µ—В—Е–Њ–і–љ–Њ–≥ –Є–Ј—А–∞–Ј–∞ –Ј–∞ –§–Ю–Я –Љ–Њ–ґ–µ —Б–µ –Є–Ј–≤–µ—Б—В–Є –Њ–±–ї–Є–Ї —Г –Ї–Њ–Љ —Ш–µ –Њ–љ–∞ —Ш–µ–і–љ–∞–Ї–∞ –Ј–∞—Ш–µ–і–љ–Є—З–Ї–Њ—Ш –њ–Њ–≤—А—И–Є–љ–Є –і–≤–∞ –Ї—А—Г–≥–∞ –Є—Б—В–Њ–≥ –њ—А–µ—З–љ–Є–Ї–∞, —З–Є—Ш–Є —Б–µ —А–∞–Ј–Љ–∞–Ї –њ–Њ –ї–Є–љ–Є—Ш–Є –Ї–Њ—Ш–∞ —Б–њ–∞—Ш–∞ —Ъ–Є—Е–Њ–≤–µ —Б—А–µ–і–Є—И—Ъ–µ —В–∞—З–Ї–µ –Љ–µ—Ъ–∞ –Њ–і –љ—Г–ї–µ –і–Њ —А–∞–Ј–Љ–∞–Ї–∞ —Ш–µ–і–љ–∞–Ї–Њ–≥ –њ—А–µ—З–љ–Є–Ї—Г (—Б–ї–Є–Ї–∞ 5; –Њ–њ—И–Є—А–љ–Є—Ш–µ –Њ –Њ–≤–Њ–Љ –Њ–±–ї–Є–Ї—Г –§–Ю–Я —Г –і–µ–ї—Г "–Ш–љ—В–µ–≥—А–∞—Ж–Є—Ш–∞ –§–Ю–Я –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞"). –Ю–≤–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–Ї–∞ –Њ–њ–µ—А–∞—Ж–Є—Ш–∞ —Б–µ –љ–∞–Ј–Є–≤–∞ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–∞ –Є, –њ–Њ—И—В–Њ —Ш–µ –њ—А–µ—З–љ–Є–Ї –і–≤–µ –Ї—А—Г–ґ–љ–Є—Ж–µ —Ш–µ–і–љ–∞–Ї –њ—А–µ—З–љ–Є–Ї—Г –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —Г –Њ–≤–Њ–Љ –њ–Њ—Б–µ–±–љ–Њ–Љ —Б–ї—Г—З–∞—Ш—Г —А–∞–і–Є —Б–µ –Њ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –£ –Њ–≤–Њ–Љ –Њ–±–ї–Є–Ї—Г, –§–Ю–Я —Б–µ –Љ–Њ–ґ–µ –Є–Ј—А–∞–Ј–Є—В–Є —Б–∞:
 ........ (4)
........ (4)
![{\displaystyle P({\vec {r}}_{p})=V({\vec {r}}_{p})\,exp[ikW({\vec {r}}_{p})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba2efee8b34de25e5b2fa4470ded8430b7063439) ........ (4.1)
........ (4.1)
–≥–і–µ —Ш–µ  —Д—Г–љ–Ї—Ж–Є—Ш–∞ (–Є–Ј–ї–∞–Ј–љ–Њ–≥) –Њ—В–≤–Њ—А–∞,
—Д—Г–љ–Ї—Ж–Є—Ш–∞ (–Є–Ј–ї–∞–Ј–љ–Њ–≥) –Њ—В–≤–Њ—А–∞,  —Ш–µ –њ–Њ–Ј–Є—Ж–Є–Њ–љ–Є –≤–µ–Ї—В–Њ—А —Г —А–∞–≤–љ–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ (—В–∞—З–љ–Є—Ш–µ, —Г —А–∞–≤–љ–Є –Є–Ј–ї–∞–Ј–љ–Њ–≥ –Њ—В–≤–Њ—А–∞), –Њ–і—А–µ—Т–µ–љ –і—Г–ґ–Є–љ–Њ–Љ –і–Њ –њ—А–Њ–Є–Ј–≤–Њ—Щ–љ–µ —В–∞—З–Ї–µ —Г –Њ–≤–Њ—Ш —А–∞–≤–љ–Є –Є —Г–≥–ї–Њ–Љ –Ї–Њ—Ш–Є –Ј–∞–Ї–ї–∞–њ–∞ —Б–∞ —Г—Б–њ—А–∞–≤–љ–Њ–Љ –Њ—Б–Њ–Љ –Њ—В–≤–Њ—А–∞.
—Ш–µ –њ–Њ–Ј–Є—Ж–Є–Њ–љ–Є –≤–µ–Ї—В–Њ—А —Г —А–∞–≤–љ–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ (—В–∞—З–љ–Є—Ш–µ, —Г —А–∞–≤–љ–Є –Є–Ј–ї–∞–Ј–љ–Њ–≥ –Њ—В–≤–Њ—А–∞), –Њ–і—А–µ—Т–µ–љ –і—Г–ґ–Є–љ–Њ–Љ –і–Њ –њ—А–Њ–Є–Ј–≤–Њ—Щ–љ–µ —В–∞—З–Ї–µ —Г –Њ–≤–Њ—Ш —А–∞–≤–љ–Є –Є —Г–≥–ї–Њ–Љ –Ї–Њ—Ш–Є –Ј–∞–Ї–ї–∞–њ–∞ —Б–∞ —Г—Б–њ—А–∞–≤–љ–Њ–Љ –Њ—Б–Њ–Љ –Њ—В–≤–Њ—А–∞.
–£ —Д—Г–љ–Ї—Ж–Є—Ш–Є –Њ—В–≤–Њ—А–∞, V —Ш–µ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ —В–∞–ї–∞—Б–љ–Њ–≥ —А–∞—Б–њ–Њ–љ–∞ –Ї—А–Њ–Ј –Њ—В–≤–Њ—А, —Ш–µ–і–љ–∞–Ї–∞ —Ш–µ–і–Є–љ–Є—Ж–Є –Ј–∞ —А–∞–≤–љ–Њ–Љ–µ—А–∞–љ –њ—А–µ–љ–Њ—Б –њ—А–µ–Ї–Њ —Ж–µ–ї–µ —Ъ–µ–≥–Њ–≤–µ –њ–Њ–≤—А—И–Є–љ–µ, –Ї=2ѕА/ќї —Ш–µ –њ–µ—А–Є–Њ–і–љ–Є –±—А–Њ—Ш, –Є W —Ш–µ –≥—А–µ—И–Ї–∞ —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞ —Г —В–∞—З–Ї–Є –Њ–і—А–µ—Т–µ–љ–Њ—Ш –њ—А–Њ—Б—В–Њ—А–љ–Є–Љ –≤–µ–Ї—В–Њ—А–Њ–Љ  . –£ –Њ–і—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞, W=0,
. –£ –Њ–і—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞, W=0, ![{\displaystyle exp[ikW({\vec {r}}_{p})]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38a233b25e2b7d69da0652eb5ac28211b6e7ba4f) –Є, —Б–∞ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Є–Љ –њ—А–µ–љ–Њ—Б–Њ–Љ —В–∞–ї–∞—Б–љ–Њ–≥ —А–∞—Б–њ–Њ–љ–∞, —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Њ—В–≤–Њ—А–∞ –Є–Љ–∞ —Ш–µ–і–Є–љ–Є—З–љ—Г –≤—А–µ–і–љ–Њ—Б—В –Є–Ј–љ–∞–і —Ж–µ–ї–µ –њ–Њ–≤—А—И–Є–љ–µ –Њ—В–≤–Њ—А–∞.
–Є, —Б–∞ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Є–Љ –њ—А–µ–љ–Њ—Б–Њ–Љ —В–∞–ї–∞—Б–љ–Њ–≥ —А–∞—Б–њ–Њ–љ–∞, —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Њ—В–≤–Њ—А–∞ –Є–Љ–∞ —Ш–µ–і–Є–љ–Є—З–љ—Г –≤—А–µ–і–љ–Њ—Б—В –Є–Ј–љ–∞–і —Ж–µ–ї–µ –њ–Њ–≤—А—И–Є–љ–µ –Њ—В–≤–Њ—А–∞.
 –°–Ы–Ш–Ъ–Р 3: –Ф–Ю–С–Ш–И–Р–К–Х –§–Ю–Я –Р–£–Ґ–Ю–Ъ–Ю–†–Х–Ы–Р–¶–Ш–И–Ю–Ь –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Ю–Ґ–Т–Ю–†–Р
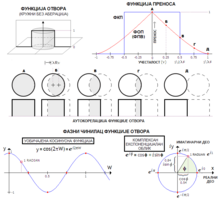
–°–Ы–Ш–Ъ–Р 3: –Ф–Ю–С–Ш–И–Р–К–Х –§–Ю–Я –Р–£–Ґ–Ю–Ъ–Ю–†–Х–Ы–Р–¶–Ш–И–Ю–Ь –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Ю–Ґ–Т–Ю–†–Р –Э–∞ —Б–ї–Є—Ж–Є –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј–∞–љ–Њ —Ш–µ –Ї–∞–Ї–Њ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–∞ –Њ–њ—А–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ –њ—А–Њ–Є–Ј–≤–Њ–і–Є –§–Ю–Я (—Г –і–∞—В–Њ–Љ —Б–ї—Г—З–∞—Ш—Г –§–Я–Т, —Ш–µ—А —Ш–µ –Ј–∞–љ–µ–Љ–∞—А–µ–љ —Д–∞–Ј–љ–Є –і–µ–Њ –§–Ю–Я). –Я—А–Є–Љ–µ—А —Ш–µ –Ј–∞ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А –±–µ–Ј –∞–±–µ—А–∞—Ж–Є—Ш–∞. –†–∞–і–Є –њ–Њ—А–µ—Т–µ—Ъ–∞, –њ—А–Є–Ї–∞–Ј–∞–љ–∞ —Ш–µ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Ї–Њ—Е–µ—А–µ–љ—В–љ–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ (–§–Ъ–Я). –£ –і–Њ—Ъ–µ–Љ –і–µ–ї—Г —Б–ї–Є–Ї–µ —Ш–µ –≤–µ–Ј–∞ –Є–Ј–Љ–µ—Т—Г —Г–Њ–±–Є—З–∞—Ш–µ–љ–Њ–≥ –Є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–≥ –Њ–±–ї–Є–Ї–∞ —В–∞–ї–∞—Б–љ–µ —Д—Г–љ–Ї—Ж–Є—Ш–µ; –≥—А–µ—И–Ї–∞ —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞ W —Ш–µ –і–∞—В–∞ —Г —Ш–µ–і–Є–љ–Є—Ж–∞–Љ–∞ —В–∞–ї–∞—Б–љ–µ –і—Г–ґ–Є–љ–µ. –£–Њ–±–Є—З–∞—Ш–µ–љ–Є –Њ–±–ї–Є–Ї —Ш–µ —Ш–µ–і–љ–∞–Ї —А–µ–∞–ї–љ–Њ–Љ (–Ї–Њ—Б–Є–љ—Г—Б–љ–Њ–Љ) –і–µ–ї—Г –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–µ —Д—Г–љ–Ї—Ж–Є—Ш–µ. –Ґ–∞–ї–∞—Б–љ–Є —А–∞—Б–њ–Њ–љ VeikѕЖ, –Є–Ј—А–∞–ґ–µ–љ –Ї–∞–Њ –њ—А–Њ–Є–Ј–≤–Њ–і —А–∞—Б–њ–Њ–љ–∞ V, —Ш–µ–і–љ–∞–Ї–Њ–≥ –њ–Њ–ї—Г–њ—А–µ—З–љ–Є–Ї—Г –Ї—А—Г–≥–∞ –Є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–≥ —Д–∞–Ј–љ–Њ–≥ —З–Є–љ–Є–Њ—Ж–∞ eikѕЖ, –Ј–Њ–≤–µ —Б–µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Є —А–∞—Б–њ–Њ–љ (–µ–љ–≥. complex amplitude).
–£ –њ—А–Є—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞, –Є–ї–Є –Ј–∞–Ї–ї–Њ–љ–∞ —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г, —В–∞–ї–∞—Б–љ–Є —А–∞—Б–њ–Њ–љ —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г –љ–Є—Ш–µ —А–∞–≤–љ–Њ–Љ–µ—А–∞–љ, –Є –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–∞ –њ—А–Њ–Є–Ј–≤–Њ–і–Є –і—А—Г–≥–∞—З–Є—Ш–Є –Њ–±–ї–Є–Ї —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞. –£ –љ–∞—З–µ–ї—Г, —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ —Г –њ—А–Є—Б—Г—Б—В–≤—Г –∞–±–µ—А–∞—Ж–Є—Ш–∞ —Ш–µ —Г–≤–µ–Ї –љ–Є–ґ–∞ –љ–µ–≥–Њ –±–µ–Ј —Ъ–Є—Е.
–§—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ї–∞–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–∞ –≤–Є—Б–Є–љ–∞
–§–Ю–Я —Ш–µ —Б–ї–Њ–ґ–µ–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Ї–Њ—Ш–∞ —Б–µ —Б–∞—Б—В–Њ—Ш–Є –Њ–і –і–≤–∞ –і–µ–ї–∞: (1) —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ, –§–Я–Т (–µ–љ–≥. Modulation transfer function, MTF), –Є (2) —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞ —Д–∞–Ј–µ, –§–Я–§ (–µ–љ–≥. Phase transfer function, PTF). –Я—А–≤–∞ –Є–Ј—А–∞–ґ–∞–≤–∞ –њ—А–Њ–Љ–µ–љ—Г –≤–Є—Б–Є–љ–µ (–Љ–Њ–і—Г–ї—Г—Б–∞) –Є–Ј–Љ–µ—Т—Г –љ–∞—Ш—Б–≤–µ—В–ї–Є—Ш–µ —В–∞—З–Ї–µ —Г —Б–≤–µ—В–ї–Њ—Ш –Є –љ–∞—Ш—В–∞–Љ–љ–Є—Ш–µ —Г —В–∞–Љ–љ–Њ—Ш –ї–Є–љ–Є—Ш–µ, —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –≤–Є—Б–Є–љ—Г —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г. –Ф—А—Г–≥–∞ –Є–Ј—А–∞–ґ–∞–≤–∞ –њ–Њ–Љ–∞–Ї –Њ–≤–µ —Б–ї–Є–Ї–µ –ї–Є–љ—Ш–∞ —Г —Б—В—А–∞–љ—Г (—Г –Њ–і–љ–Њ—Б—Г –љ–∞ —Ъ–Є—Е–Њ–≤—Г –У–∞—Г—Б–Њ–≤—Б–Ї—Г —Б–ї–Є–Ї—Г) –Є–Ј–∞–Ј–≤–∞–љ –њ—А–Њ–Љ–µ–љ–Њ–Љ —Г —А–∞—Б–њ–Њ—А–µ–і—Г –µ–љ–µ—А–≥–Є—Ш–µ –§–®–Ґ –Ј–±–Њ–≥ –∞–±–µ—А–∞—Ж–Є—Ш–∞. –Ю–і–љ–Њ—Б –Є–Ј–Љ–µ—Т—Г –§–Ю–Я, –§–Я–Т –Є –§–Я–§ –Љ–Њ–ґ–µ —Б–µ –њ—А–µ–і—Б—В–∞–≤–Є—В–Є –Ї–∞–Њ:
- –§–Ю–Я = |–§–Ю–Я|ei–§–Я–§ = –§–Я–Тei–§–Я–§ ........ (5)
—И—В–Њ –Ј–љ–∞—З–Є –і–∞ —Ш–µ –§–Я–Т —Ш–µ–і–љ–∞–Ї–∞ –∞–њ—Б–Њ–ї—Г—В–љ–Њ—Ш –≤—А–µ–і–љ–Њ—Б—В–Є –§–Ю–Я (–µ=2.71828... —Ш–µ –Њ—Б–љ–Њ–≤–∞ –њ—А–Є—А–Њ–і–љ–Њ–≥ –ї–Њ–≥–∞—А–Є—В–Љ–∞).
–Ш–Ј —Ш–µ–і–љ–∞–Ї–Њ—Б—В–Є –µi–§–Я–§ = cos(–§–Я–§) + isin(–§–Я–§), –і–≤–∞ –і–µ–ї–∞ –§–Ю–Я –Љ–Њ–≥—Г —Б–µ –Є–Ј—А–∞–Ј–Є—В–Є –Ї–∞–Њ:
- –§–Ю–Я = –§–Я–Т[cos(FPF)+isin(–§–Я–§)] = –§–Я–Тcos(–§–Я–§)+–§–Я–Тisin(–§–Я–§) ........ (6)
–≥–і–µ —Б—Г –і–≤–∞ —З–Є–љ–Є–Њ—Ж–∞ –љ–∞ –і–µ—Б–љ–Њ—Ш —Б—В—А–∞–љ–Є —Б—В–≤–∞—А–љ–Є (–њ—А–≤–Є) –Є –Є–Љ–∞–≥–Є–љ–∞—А–љ–Є –і–µ–Њ –§–Ю–Я (—Г–Ј –љ–∞–њ–Њ–Љ–µ–љ—Г –і–∞ —Б–µ –§–Я–§ –Њ–±–Є—З–љ–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ –Ї–∞–Њ —Г–≥–∞–Њ). –Ю–љ–Є –Љ–Њ–≥—Г –±–Є—В–Є –Є –≥—А–∞—Д–Є—З–Ї–Є –њ—А–Є–Ї–∞–Ј–∞–љ–Є –Њ–і–≤–Њ—Ш–µ–љ–Њ, –њ—А–≤–Є –Ї–∞–Њ –Ї–Њ—Б–Є–љ—Г—Б–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –Ї–Њ—Ш–∞ –њ–Њ—З–Є—Ъ–µ —Б–∞ 1 –Ј–∞ –і—Г–ґ–Є–љ—Б–Ї—Г —Д—А–µ–Ї–≤–µ–љ—Ж–Є—Ш—Г –§–Ю–Я —Ш–µ–і–љ–∞–Ї–Њ—Ш –љ—Г–ї–Є, –∞ –і—А—Г–≥–Є –Ї–∞–Њ —Б–Є–љ—Г—Б–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ–Њ—З–Є—Ъ—Г—Ы–Є —Б–∞ –љ—Г–ї–Њ–Љ –Ј–∞ –Є—Б—В—Г —Д—А–µ–Ї–≤–µ–љ—Ж–Є—Ш—Г.
 –°–Ы–Ш–Ъ–Р 4: –Ш–Љ–∞–≥–Є–љ–∞—А–љ–Є –Є —Б—В–≤–∞—А–љ–Є –і–µ–Њ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ (–§–Ю–Я)
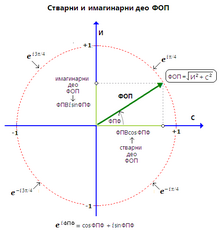
–°–Ы–Ш–Ъ–Р 4: –Ш–Љ–∞–≥–Є–љ–∞—А–љ–Є –Є —Б—В–≤–∞—А–љ–Є –і–µ–Њ —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ (–§–Ю–Я) –°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј—Г—Ш–µ –Њ–і–љ–Њ—Б –Є–Ј–Љ–µ—Т—Г –§–Ю–Я –Є —Ъ–µ–љ–Њ–≥ –Є–Љ–∞–≥–Є–љ–∞—А–љ–Њ–≥ –Є —Б—В–≤–∞—А–љ–Њ–≥ –і–µ–ї–∞. –Ъ—А—Г–ґ–љ–Є—Ж–∞ - –Ј–≤–∞–љ–∞ —Ш–µ–і–Є–љ–Є—З–љ–Є —В–∞–ї–∞—Б–љ–Є, –Є–ї–Є —Д–∞–Ј–љ–Є –Ї—А—Г–≥, —З–Є—Ш–Є –њ–Њ–ї—Г–њ—А–µ—З–љ–Є–Ї –Є–Љ–∞ —Ш–µ–і–Є–љ–Є—З–љ—Г –≤—А–µ–і–љ–Њ—Б—В - –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –§–Я–§, –Њ–і–љ–Њ—Б–љ–Њ –±–Њ—З–љ–Є –њ–Њ–Љ–∞–Ї —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞ –Є–Ј—А–∞–ґ–µ–љ –Ї–∞–Њ –њ—А–Њ–Љ–µ–љ–∞ —Г —Д–∞–Ј–Є —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –њ–Њ–ї–Њ–ґ–∞—Ш —Б–ї–Є–Ї–µ —Б–∞ –љ—Г–ї—В–Є–Љ –њ–Њ–Љ–∞–Ї–Њ–Љ. –Ч–∞ –±–Є–ї–Њ –Ї–Њ—Ш—Г –≤—А–µ–і–љ–Њ—Б—В –§–Я–§ –Є–Ј—Г–Ј–µ–≤ 0 –Є ѕА, –≤–Є—Б–Є–љa –§–Ю–Я (—В—Ш. –§–Я–Т), –і–∞—Вa –Ї–∞–Њ —Ш–µ–і–Є–љ–Є—З–љ–∞ –≤—А–µ–і–љ–Њ—Б—В, –Њ—Б—В–∞—Ш–µ –љ–µ–њ—А–Њ–Љ–µ—Ъ–µ–љ –Є –љ–µ–Ј–∞–≤–Є—Б–∞–љ –Њ–і –њ—А–Њ–Љ–µ–љ–∞ —Г —Б—В–≤–∞—А–љ–Њ–Љ –Є –Є–Љ–∞–≥–Є–љ–∞—А–љ–Њ–Љ –і–µ–ї—Г. –£ –Њ–≤–Њ–Љ —Б–ї—Г—З–∞—Ш—Г, –§–Ю–Я —Ш–µ —Ш–µ–і–љ–∞–Ї–∞ –Ї–≤–∞–і—А–∞—В–љ–Њ–Љ –Ї–Њ—А–µ–љ—Г —Х–±–Є—А–∞ –Ї–≤–∞–і—А–∞—В–∞ —Б–≤–Њ–≥ –Є–Љ–∞–≥–Є–љ–∞—А–љ–Њ–≥ –Є —Б—В–≤–∞—А–љ–Њ–≥ –і–µ–ї–∞.
–Р–Ї–Њ —Ш–µ –§–Я–§, —В—Ш. –±–Њ—З–љ–Є –њ–Њ–Љ–∞–Ї —Б–ї–Є–Ї–µ, 0 –Є–ї–Є ѕА, –Є–Љ–∞–≥–Є–љ–∞—А–љ–Є –і–µ–Њ —Б–µ —Б–≤–Њ–і–Є –љ–∞ –љ—Г–ї—Г, –∞ –§–Ю–Я —Б–µ –Є–Ј—Ш–µ–і–љ–∞—З—Г—Ш–µ —Б–∞ —Ъ–µ–љ–Є–Љ —Б—В–≤–∞—А–љ–Є–Љ –і–µ–ї–Њ–Љ, —В—Ш. –њ–Њ—Б—В–∞—Ш–µ —Б—В–≤–∞—А–љ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞. –Ш–Ј —Б–≤–µ–≥–∞ –Њ–≤–Њ–≥ –≤–Є–і–Є —Б–µ –і–∞ –Є–Ј—А–∞–Ј (6) –Ї–Њ—Ш–Є –Њ–њ–Є—Б—Г—Ш–µ –§–Ю–Я –љ–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –Ј–±–Є—А, –Љ–∞–і–∞ —Б–∞–і—А–ґ–Є –Ј–љ–∞–Ї –њ–ї—Г—Б, –љ–µ–≥–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–µ —Г —Д–∞–Ј–љ–Њ–Љ (—В–∞–ї–∞—Б–љ–Њ–Љ) –Ї—А—Г–≥—Г, –Њ–і—А–µ—Т–µ–љ–µ —Д–∞–Ј–љ–Є–Љ –њ–Њ–Љ–∞–Ї–Њ–Љ –§–Ю–Я.
–Р–Ї–Њ –§–®–Ґ –Є–Љ–∞ –±–Є–ї–Њ –Ї–Њ—Ш–Є –Њ–±–ї–Є–Ї —Б–Є–Љ–µ—В—А–Є—Ш–µ –Њ–Ї–Њ –ї–Є–љ–Є—Ш–µ –Ї–Њ—Ш–∞ —Ш–µ –і–µ–ї–Є –љ–∞ –і–≤–∞ –і–µ–ї–∞, –Є–Љ–∞–≥–Є–љ–∞—А–љ–Є –і–µ–Њ –љ–µ—Б—В–∞—Ш–µ (—Ш–µ—А —Г —В–Њ–Љ —Б–ї—Г—З–∞—Ш—Г —Д–∞–Ј–љ–Є –њ–Њ–Љ–∞–Ї –Љ–Њ–ґ–µ –±–Є—В–Є –Є–ї–Є –љ—Г–ї–∞ –Є–ї–Є ѕА, –≥–і–µ –Њ–≤–∞—Ш –і—А—Г–≥–Є –Љ–Њ–ґ–µ –і–∞ –њ—А–Њ—Г–Ј—А–Њ–Ї—Г—Ш–µ –Њ–±—А–љ—Г—В–Є –Ї–Њ–љ—В—А–∞—Б—В, –±–µ–Ј –±–Њ—З–љ–Њ–≥ –њ–Њ–Љ–∞–Ї–∞ —Б–ї–Є–Ї–µ), –Є –§–Ю–Я —Б–µ —Б–≤–Њ–і–Є –љ–∞ –§–Ю–Я = –§–Я–Тcos(–§–Я–§). –Ю–≤–Њ —Ш–µ —Б–ї—Г—З–∞—Ш —Б–∞ –і–µ—Д–Њ–Ї—Г—Б–Њ–Љ, —Б—Д–µ—А–љ–Њ–Љ –∞–±–µ—А–∞—Ж–Є—Ш–Њ–Љ –Є –∞—Б—В–Є–≥–Љ–∞—В–Є–Ј–Љ–Њ–Љ, –Ј–∞ –±–Є–ї–Њ –Ї–Њ—Ш—Г –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш—Г –§–®–Ґ, –∞ –Ј–∞ –Ї–Њ–Љ—Г —Б–∞–Љ–Њ –Ј–∞ —Ш–µ–і–љ—Г –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш—Г, –і—Г–ґ –Њ—Б–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ (–Ј–∞ —Б–≤–µ –Њ—Б—В–∞–ї–µ –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш–∞ –§–®–Ґ –Ј–∞ –Ї–Њ–Љ—Г, –§–Ю–Я —Б–µ —Б–∞—Б—В–Њ—Ш–Є –Њ–і –Њ–±–∞ –і–µ–ї–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ, —Б—В–≤–∞—А–љ–Њ–≥ –Є –Є–Љ–∞–≥–Є–љ–∞—А–љ–Њ–≥).
–Я—А–Њ—Б—В–Њ—А–љ–∞ —Б–≤–Њ—Ш—Б—В–≤–∞ –§–Ю–Я
–Ь–∞–і–∞ —Б–µ –§–Ю–Я –љ–∞—Ш—З–µ—И—Ы–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –Ї–∞–Њ –і–≤–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–∞–љ –≥—А–∞—Д —Ъ–µ–љ–Њ–≥ –і–µ–ї–∞ –Ї–Њ—Ш–Є –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –њ—А–Њ–Љ–µ–љ—Г –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞ —Б–∞ —Г—З–µ—Б—В–∞–ї–Њ—И—Ы—Г, —В—Ш. –§–Я–Т, –Њ–љ–∞ —Ш–µ —Г –њ–Њ—В–њ—Г–љ–Њ—Б—В–Є –Њ–њ–Є—Б–∞–љ–∞ —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–Њ–Љ —Д–Є–≥—Г—А–Њ–Љ, –Ї–Њ—Ш–∞ –њ—А–Њ–Є—Б—В–Є—З–µ –Є–Ј —Б–∞–Љ–Њ–≥ –Є–љ—В–µ–≥—А–∞—Ж–Є–Њ–љ–Њ–≥ –њ—А–Њ—Ж–µ—Б–∞ –Ї–Њ—Ш–Є–Љ —Б–µ –і–Њ–±–Є—Ш–∞ –§–Ю–Я. –Ю–≤–∞—Ш –њ—А–Њ—Ж–µ—Б —Б–µ –Љ–Њ–ґ–µ –Є–Ј—А–∞–Ј–Є—В–Є –љ–∞ –≤–Є—И–µ —А–∞–Ј–ї–Є—З—В–Є—Е –љ–∞—З–Є–љ–∞, –∞ –љ–∞ —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ—Г —Д–Є–≥—Г—А—Г –љ–µ–њ–Њ—Б—А–µ–і–љ–Њ —Г–Ї–∞–Ј—Г—Ш–µ –Є–Ј—А–∞–Ј —Г –Ї–Њ–Љ–µ —Ш–µ –§–Ю–Я –і–Њ–±–Є—Ш–µ–љ–∞ –Є–љ—В–µ–≥—А–∞—Ж–Є—Ш–Њ–Љ –љ–∞ –њ–Њ–≤—А—И–Є–љ–Є –њ—А–µ–Ї–ї–∞–њ–∞—Ъ–∞ –і–≤–∞ –Њ—В–≤–Њ—А–∞ –Є—Б—В–Њ–≥ –њ—А–µ—З–љ–Є–Ї–∞, —Ш–µ–і–љ–∞–Ї–Њ–≥ –њ—А–µ—З–љ–Є–Ї—Г –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ –Ј–∞ –Ї–Њ—Ш–Є —Б–µ –§–Ю–Я –Є–Ј—А–∞—З—Г–љ–∞–≤–∞ (–Љ–∞—В–µ–Љ–∞—В–Є—З–Ї–Є –љ–∞–Ј–Є–≤ –Ј–∞ –Њ–≤—Г –Њ–њ–µ—А–∞—Ж–Є—Ш—Г —Ш–µ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–∞; —Г –Њ–≤–Њ–Љ —Б–ї—Г—З–∞—Ш—Г, —А–∞–і–Є —Б–µ –Њ –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞).
–Ш–љ—В–µ–≥—А–∞—Ж–Є—Ш–∞ –§–Ю–Я –∞—Г—В–Њ–Ї–Њ—А–µ–ї–∞—Ж–Є—Ш–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞
–Ш–љ—В–µ–≥—А–∞—Ж–Є—Ш–∞ —Б–µ –≤—А—И–Є –Ј–∞ —А–∞—Б–њ–Њ–љ —Г —А–∞–Ј–Љ–∞–Ї—Г —Ж–µ–љ—В–∞—А–∞ –і–≤–µ –Ї—А—Г–ґ–љ–Є—Ж–µ –Њ–і –љ—Г–ї–∞ - –Ї–∞–і–∞ —Б–µ –Ї—А—Г–ґ–љ–Є—Ж–µ —Г –њ–Њ—В–њ—Г–љ–Њ—Б—В–Є –њ—А–µ–Ї–ї–∞–њ–∞—Ш—Г –Є –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Ш–µ –љ–∞—Ш–≤–µ—Ы–Є –Љ–Њ–≥—Г—Ы–Є (1) - –і–Њ —А–∞–Ј–Љ–∞–Ї–∞ —Ш–µ–і–љ–∞–Ї–Њ–≥ –њ—А–µ—З–љ–Є–Ї—Г –Ї—А—Г–ґ–љ–Є—Ж–µ, –Ї–∞–і –њ—А–µ–љ–Њ—Б –њ–∞–і–∞ –љ–∞ –љ—Г–ї—Г. –†–∞–Ј–Љ–∞–Ї –Є–Ј–Љ–µ—Т—Г —Ж–µ–љ—В–∞—А–∞ —Ш–µ —Ш–µ–і–љ–∞–Ї —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, –Є –≤–Є—Б–Є–љ–∞ –њ—А–µ–љ–Њ—Б–∞ –Ј–∞ —Б–≤–∞–Ї–Є –і–∞—В–Є —А–∞–Ј–Љ–∞–Ї —Ш–µ —Ш–µ–і–љ–∞–Ї–∞ –њ—А–µ–љ–Њ—Б—Г –Ј–∞ —В—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В.
–Ю–≤–∞—Ш –Њ—В–≤–Њ—А –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –њ–Њ—Щ–µ —Б–Є–ї–µ (—В—Ш. —А–∞—Б–њ–Њ—А–µ–і –∞–Љ–њ–ї–Є—В—Г–і–µ —Б–≤–µ—В–ї–Њ—Б–љ–Њ–≥ –Ј—А–∞—З–µ—Ъ–∞) —Г —А–∞–≤–љ–Є –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –Ч–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А, –∞–Љ–њ–ї–Є—В—Г–і–∞ —Ш–µ –љ–µ–њ—А–Њ–Љ–µ—Ъ–µ–љ–∞ –њ—А–µ–Ї–Њ —Ж–µ–ї–µ –њ–Њ–≤—А—И–Є–љ–µ –Њ—В–≤–Њ—А–∞, –∞ –≤–Є—Б–Є–љ–∞ –њ—А–µ–љ–Њ—Б–∞ –§–Ю–Я —Ш–µ —Б—А–∞–Ј–Љ–µ—А–љ–∞ –Ї–Њ–ї–Є—З–љ–Є–Ї—Г –њ–Њ–≤—А—И–Є–љ–µ –њ—А–µ–Ї–ї–∞–њ–∞—Ъ–∞ –Є –њ–Њ–≤—А—И–Є–љ–µ —Ж–µ–ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –Ю–≤–∞—Ш –њ—А–µ–љ–Њ—Б —Ш–µ —Ш–µ–і–Є–љ–Є—З–љ –њ—А–µ–љ–Њ—Б –њ—А–µ–Љ–∞ –Ї–Њ–Љ–µ —Б–µ –Љ–µ—А–Є –≤–µ–ї–Є—З–Є–љ–∞ –њ—А–µ–љ–Њ—Б–∞, —В—Ш. –§–Ю–Я, –љ–µ—Б–∞–≤—А—И–µ–љ–Є—Е –Њ–њ—В–Є—З–Ї–Є—Е –Њ—В–≤–Њ—А–∞.
–£ —Б–ї—Г—З–∞—Ш—Г –љ–µ—Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —Б–∞ –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Є–Љ —А–∞—Б–њ–Њ—А–µ–і–Њ–Љ –∞–Љ–њ–ї–Є—В—Г–і–µ —Г–љ—Г—В–∞—А –Њ–≤–µ —А–∞–≤–љ–Є, –±–Є–ї–Њ –Ј–±–Њ–≥ –њ—А–Є—Б—Г—Б—В–≤–∞ –∞–±–µ—А–∞—Ж–Є—Ш–∞ –Є–ї–Є –Ј–∞–Ї–ї–Њ–љ–∞, –≤–Є—Б–Є–љ–∞ –њ—А–µ–љ–Њ—Б–∞ –љ–µ –Ј–∞–≤–Є—Б–Є —Б–∞–Љ–Њ –Њ–і –њ–Њ–≤—А—И–Є–љ–µ –њ—А–µ–Ї–ї–∞–њ–∞—Ъ–∞ –љ–µ–≥–Њ –Є –Њ–і —А–∞—Б–њ–Њ—А–µ–і–∞ –∞–Љ–њ–ї–Є—В—Г–і–µ. –Р–Ї–Њ —Ш–µ –Њ–≤–∞—Ш —А–∞—Б–њ–Њ—А–µ–і —А–∞–і–Є—Ш–∞–ї–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–∞–љ, –њ—А–µ–љ–Њ—Б –Є–Љ–∞ –Є—Б—В—Г –≤–Є—Б–Є–љ—Г –Ј–∞ —Б–≤–∞–Ї–Є —Г–≥–∞–Њ –њ—А–µ–Ї–ї–∞–њ–∞—Ъ–∞ –Ј–∞ –і–∞—В—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В. –£ —Б–ї—Г—З–∞—Ш—Г –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–≥ —А–∞—Б–њ–Њ—А–µ–і–∞, –≤–Є—Б–Є–љ–∞ —Б–µ –Љ–µ—Ъ–∞ —Б–∞ –њ—А–Њ–Љ–µ–љ–Њ–Љ —Г–≥–ї–∞, —И—В–Њ –Ј–∞ –њ–Њ—Б–ї–µ–і–Є—Ж—Г –Є–Љ–∞ –∞—Б–Є–Љ–µ—В—А–Є—З–љ—Г —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ—Г —Д–Є–≥—Г—А—Г –§–Ю–Я.
 –°–Ы–Ш–Ъ–Р 5: –Ш–Ы–£–°–Ґ–†–Р–¶–Ш–И–Р –Ш–Э–Ґ–Х–У–†–Р–Ы–Э–Ю–У –Я–†–Ю–¶–Х–°–Р –§–£–Э–Ъ–¶–Ш–И–Х –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р
–°–Ы–Ш–Ъ–Р 5: –Ш–Ы–£–°–Ґ–†–Р–¶–Ш–И–Р –Ш–Э–Ґ–Х–У–†–Р–Ы–Э–Ю–У –Я–†–Ю–¶–Х–°–Р –§–£–Э–Ъ–¶–Ш–И–Х –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј—Г—Ш–µ —И–µ–Љ—Г –Њ–≤–Њ–≥ –Є–љ—В–µ–≥—А–∞–ї–љ–Њ–≥ –њ—А–Њ—Ж–µ—Б–∞. –Ч–∞ —Б–≤–∞–Ї—Г –і–∞—В—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В —Б–Є–≥–љ–∞–ї–∞ (ќљ), –Ї–Њ—Ш–∞ —Б–µ –Ї—А–µ—Ы–µ —Г —А–∞—Б–њ–Њ–љ—Г –Њ–і 0 –і–Њ 1 —Г —Ш–µ–і–Є–љ–Є—Ж–∞–Љ–∞ –Њ–±—А–љ—Г—В–µ –≥—А–∞–љ–Є—З–љ–µ –і—Г–ґ–љ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є 1/ќїF, —Ш–µ–і–∞–љ –Њ–і –Њ—В–≤–Њ—А–∞ –Њ–њ–Є—Б—Г—Ш–µ –њ—Г–љ –Ї—А—Г–≥ –Њ–Ї–Њ –і—А—Г–≥–Њ–≥, —Б—А–µ–і–Є—И—Ъ–µ–≥ –Њ—В–≤–Њ—А–∞ (R –љ–∞ —Б–ї–Є—Ж–Є —Ш–µ —А–∞–і–Є—Ш—Г—Б –Ј–∞–Ї—А–Є–≤—Щ–µ–љ–Њ—Б—В–Є —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞, —В–µ —Ш–µ ќїRќљ –Ј–∞ –≥—А–∞–љ–Є—З–љ—Г –і—Г–ґ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В —Ш–µ–і–љ–∞–Ї–Њ –њ—А–µ—З–љ–Є–Ї—Г –Њ—В–≤–Њ—А–∞). –Ґ–Є–Љ–µ —Б–µ –µ—Д–µ–Ї—В–Є–≤–љ–Њ –Љ–µ—Ъ–∞ –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш–∞ –ї–Є–љ–Є—Ш–∞ –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –§–®–Ґ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –Ю–≤–Њ –Ј–љ–∞—З–Є –і–∞ –Ј–∞ —Б–≤–∞–Ї—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В —Г —А–∞—Б–њ–Њ–љ—Г –Њ–і –љ—Г–ї–µ –і–Њ 1/ќїF, –Є–љ—В–µ–≥—А–∞—Ж–Є–Њ–љ–Є –њ—А–Њ—Ж–µ—Б –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–і—Б—В–∞–≤–Є –Ї—А—Г–ґ–љ–Њ–Љ –ї–Є–љ–Є—Ш–Њ–Љ —З–Є—Ш–Є —Ш–µ –њ–Њ–ї—Г–њ—А–µ—З–љ–Є–Ї —Б—А–∞–Ј–Љ–µ—А–∞–љ –і–∞—В–Њ—Ш —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, –∞ –≤–Є—Б–Є–љ–∞ —Г —Б–≤–∞–Ї–Њ—Ш —В–∞—З–Ї–Є –Ј–∞–≤–Є—Б–Є –Њ–і –Љ–µ—Т—Г—Б–Њ–±–љ–Њ–≥ –њ–Њ–ї–Њ–ґ–∞—Ш–∞ —Б–Є–љ—Г—Б–Њ–Є–і–љ–Є—Е –ї–Є–љ–Є—Ш–∞ –Є –§–®–Ґ. –°–≤–µ –Њ–≤–µ –Ї—А—Г–ґ–љ–µ –ї–Є–љ–Є—Ш–µ, –і–Њ–і–∞–љ–µ —Ш–µ–і–љ–∞ –љ–∞ –і—А—Г–≥—Г, —Б—В–≤–∞—А–∞—Ш—Г –Ї—Г–њ–∞—Б—В—Г —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ—Г —Д–Є–≥—Г—А—Г —З–Є—Ш–∞ —Ш–µ –Њ—Б–љ–Њ–≤–∞ –Ї—А—Г–ґ–љ–Є—Ж–∞ –≥—А–∞–љ–Є—З–љ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є, –∞ –≤—А—Е —Ш–µ —В–∞—З–Ї–∞ –љ–∞ –љ–µ–њ—А–Њ–Љ–µ—Ъ–Є–≤–Њ—Ш —Ш–µ–і–Є–љ–Є—З–љ–Њ—Ш –≤–Є—Б–Є–љ–Є –Ј–∞ –љ—Г–ї—В—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В.
–£–Њ–±–Є—З–∞—Ш–µ–љ–Є –і–≤–Њ–і–Є–Љ–µ–љ–Ј–Є–љ–∞–ї–∞–љ –Њ–±–ї–Є–Ї –§–Ю–Я —Ш–µ –њ—А–µ—Б–µ–Ї –Њ–≤–µ —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–µ –§–Ю–Я —Г —В–∞–љ–≥–µ–љ—Ж–Є—Ш–∞–ї–љ–Њ—Ш —А–∞–≤–љ–Є –§–®–Ґ. –£ —Б–ї—Г—З–∞—Ш–µ–≤–Є–Љ–∞ –Ї–∞–і —Ш–µ –§–®–Ґ —А–∞–і–Є—Ш–∞–ї–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–љ–∞ (–љ–∞ –њ—А–Є–Љ–µ—А, –Ј–∞ –і–µ—Д–Њ–Ї—Г—Б, —Б—Д–µ—А–љ—Г –∞–±–µ—А–∞—Ж–Є—Ш—Г, –Є–ї–Є —Г —Б–ї—Г—З–∞—Ш—Г –њ—А—Б—В–µ–љ–∞—Б—В–Њ–≥ –Њ—В–≤–Њ—А–∞), –Њ–і–≥–Њ–≤–∞—А–∞—Ш—Г—Ы–∞ —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–∞ –§–Ю–Я —Ш–µ —В–∞–Ї–Њ—Т–µ —А–∞–і–Є—Ш–∞–ї–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–љ–∞, —В–µ —Ш–µ —Г –њ–Њ—В–њ—Г–љ–Њ—Б—В–Є –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ–∞ —Ъ–µ–љ–Є–Љ –і–≤–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–Є–Љ –њ—А–µ—Б–µ–Ї–Њ–Љ.
–Ь–µ—Т—Г—В–Є–Љ, —Г —Б–ї—Г—З–∞—Ш—Г —А–∞–і–Є—Ш–∞–ї–љ–Њ –∞—Б–Є–Љ–µ—В—А–Є—З–љ–µ –§–®–Ґ (–љ–∞ –њ—А–Є–Љ–µ—А, —Г —Б–ї—Г—З–∞—Ш—Г –Ї–Њ–Љ–µ, –∞—Б—В–Є–≥–Љ–∞—В–Є–Ј–Љ–∞, –Є–ї–Є –і—А—Г–≥–Є—Е –∞—Б–Є–Љ–µ—В—А–Є—З–љ–Є—Е –∞–±–µ—А–∞—Ж–Є—Ш–∞), —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–∞ –§–Ю–Я —Ш–µ —В–∞–Ї–Њ—Т–µ —А–∞–і–Є—Ш–∞–ї–љ–Њ –∞—Б–Є–Љ–µ—В—А–Є—З–љ–∞, –Є –љ–Є—Ш–µ–і–∞–љ —Ъ–µ–љ –њ—А–µ—Б–µ–Ї –љ–∞ –і–∞—Ш–µ –њ—Г–љ—Г —Б–ї–Є–Ї—Г –µ—Д–µ–Ї—В–∞ —В–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ –љ–∞ –Ї–∞–Ї–≤–Њ—Ы—Г –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ.
–Ю–≤–Њ —Ш–µ –Њ—З–µ–Ї–Є–≤–∞–љ–∞ –њ–Њ—Б–ї–µ–і–Є—Ж–∞ —З–Є—Ъ–µ–љ–Є—Ж–µ –і–∞ —Б–µ —А–∞—Б–њ–Њ—А–µ–і –µ–љ–µ—А–≥–Є—Ш–µ —А–∞–і–Є—Ш–∞–ї–љ–Њ –∞—Б–Є–Љ–µ—В—А–Є—З–љ–µ –§–®–Ґ –і—Г–ґ –ї–Є–љ—Ш–µ —Ъ–µ–љ–Њ–≥ —Ж–µ–љ—В—А–∞–ї–љ–Њ–≥ –њ—А–µ—Б–µ–Ї–∞ –Љ–µ—Ъ–∞ —Б–∞ —А–∞–і–Є—Ш–∞–ї–љ–Є–Љ —Г–≥–ї–Њ–Љ —В–Њ–≥ –њ—А–µ—Б–µ–Ї–∞. –°–∞–Љ–Є–Љ —В–Є–Љ, —А–∞–Ј–ї–Є—З–Є—В–µ –Њ—А–Є—Ш–µ–љ—В–∞—Ж–Є—Ш–µ –§–®–Ґ, —В—Ш. —Б–ї–Є–Ї–µ —В–∞—З–Ї–µ –Ї–Њ—Ш—Г –Њ–љ–∞ –њ—А–µ–і—Б—В–∞–≤—Щ–∞, —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –љ–Є–Ј –њ–∞—А–∞–ї–µ–ї–љ–Є—Е —Б–≤–µ—В–ї–Є—Е –Є —В–∞–Љ–љ–Є—Е –ї–Є–љ–Є—Ш–∞ –Ї–Њ—Ш–µ —Б–µ –њ—Г—В–µ–Љ —Ъ–µ –њ—А–µ—Б–ї–Є–Ї–∞–≤–∞—Ш—Г, –њ–Њ–≥–∞—Т–∞—Ш—Г –Ї–∞–Ї–≤–Њ—Ы—Г —Б–ї–Є–Ї–µ –Њ–≤–Є—Е –ї–Є–љ–Є—Ш–∞ —Г —А–∞–Ј–ї–Є—З–Є—В–Њ—Ш –Љ–µ—А–Є (–љ–∞ –њ—А–Є–Љ–µ—А, –∞–Ї–Њ —Ш–µ –њ—А–µ—Б–µ–Ї –§–®–Ґ –і—Г–ґ –Ї–Њ–≥ —Ш–µ —И–Є—А–µ—Ъ–µ –µ–љ–µ—А–≥–Є—Ш–µ –љ–∞—Ш–≤–µ—Ы–µ –њ–∞—А–∞–ї–µ–ї–∞–љ —Б–∞ —Б–≤–µ—В–ї–Є–Љ –Є —В–∞–Љ–љ–Є–Љ –ї–љ–Є—Ш–∞–Љ–∞, –µ—Д–µ–Ї–∞—В –љ–∞ –Ї–≤–∞–ї–Є—В–µ—В —Б–ї–Є–Ї–µ —Ш–µ –Љ–∞—Ъ–Є –љ–µ–≥–Њ –Ї–∞–і —Ш–µ —В–∞—Ш –њ—А–µ—Б–µ–Ї –§–®–Ґ –њ–Њ—Б—В–∞–≤—Щ–µ–љ –њ–Њ–њ—А–µ—З–љ–Њ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ —Ъ–Є—Е).
–Ф–≤–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–∞ –Є —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–∞ –§–Ю–Я
 –°–Ы–Ш–Ъ–Р 6: –Ф–Т–Ю–Ф–Ш–Ь–Х–Э–Ч–Ш–Ю–Э–Р–Ы–Э–Р –Ш –Ґ–†–Ю–Ф–Ш–Ь–Х–Э–Ч–Ш–Ю–Э–Р–Ы–Э–Р –§–£–Э–Ъ–¶–Ш–И–Р –Я–†–Х–Э–Ю–°–Р –Т–Ш–°–Ш–Э–Х (–§–Я–Т)
–°–Ы–Ш–Ъ–Р 6: –Ф–Т–Ю–Ф–Ш–Ь–Х–Э–Ч–Ш–Ю–Э–Р–Ы–Э–Р –Ш –Ґ–†–Ю–Ф–Ш–Ь–Х–Э–Ч–Ш–Ю–Э–Р–Ы–Э–Р –§–£–Э–Ъ–¶–Ш–И–Р –Я–†–Х–Э–Ю–°–Р –Т–Ш–°–Ш–Э–Х (–§–Я–Т)
–°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј—Г—Ш–µ —Г–Њ–±–Є—З–∞—Ш–µ–љ—Г –і–≤–Њ–і–Є–Љ–µ–љ–Ј–Њ–љ–∞–ї–љ—Г –§–Ю–Я (–њ–Њ—И—В–Њ —Б–µ —А–∞–і–Є –Њ —Ъ–µ–љ–Њ–Љ –і–µ–ї—Г –Ї–Њ—Ш–Є –Є–Ј—А–∞–ґ–∞–≤–∞ –≤–Є—Б–Є–љ—Г –њ—А–µ–љ–Њ—Б–∞, –§–Я–Т, –љ–∞—Ш—З–µ—И—Ы–µ —Б–µ —В–∞–Ї–Њ –Є –љ–∞–Ј–Є–≤–∞), –Ї–∞–Њ –Є –Њ–і–≥–Њ–≤–∞—А–∞—Ш—Г—Ы—Г —В—А–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ—Г –§–Ю–Я/–§–Я–Т –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А, –Є –Ј–∞ –Њ—В–≤–Њ—А —Б–∞ –Ј–љ–∞—З–∞—Ш–љ–Є–Љ –љ–Є–≤–Њ–Њ–Љ –Њ–њ—В–Є—З–Ї–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ (—В–∞–љ–≥–µ–љ—Ж–Є–Њ–љ–∞–ї–љ–∞ —А–∞–≤–∞–љ –љ–∞ —Б–ї–Є—Ж–Є —Ш–µ –њ–Њ –њ—А–∞–≤–Є–ї—Г —Г—Б–њ—А–∞–≤–љ–∞ —А–∞–≤–∞–љ –Ї–Њ—Ш–∞ —Б–∞–і—А–ґ–Є –Њ–њ—В–Є—З–Ї—Г –Њ—Б—Г –Є –≥–ї–∞–≤–љ–Є –Ј—А–∞–Ї, –њ—А–µ—Б–µ—Ж–∞—Ш—Г—Ы–Є –Њ—А—В–Њ–≥–љ–∞–ї–љ—Г –љ–∞ —Ъ—Г —А–∞–≤–∞–љ —Б–ї–Є–Ї–µ –і—Г–ґ –Њ—Б–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ; —Б–∞–≥–Є—В–∞–ї–љ–∞ —А–∞–≤–∞–љ —Ш–µ —А–∞–≤–∞–љ –Ї–Њ—Ш–∞ —Б–∞–і—А–ґ–Є –Њ–њ—В–Є—З–Ї—Г –Њ—Б—Г, –Є –љ–Њ—А–Љ–∞–ї–љ–∞ —Ш–µ –љ–∞ —В–∞–љ–≥–µ–љ—Ж–Є–Њ–љ–∞–ї–љ—Г —А–∞–≤–∞–љ).
–Ч–∞ –і–∞—В–Є –і–≤–Њ–і–Є–Љ–µ–љ–Ј–Є–Њ–љ–∞–ї–љ–Є –њ—А–µ—Б–µ–Ї –§–Ю–Я - –Ї–Њ—Ш–∞ —Ш–µ, –Ї–∞–Њ —И—В–Њ —Ш–µ –љ–∞–њ–Њ–Љ–µ–љ—Г—В–Њ –Њ–±–Є—З–љ–Њ –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ–∞ —Ъ–µ–љ–Є–Љ –і–µ–ї–Њ–Љ –Ї–Њ—Ш–Є –Њ–њ–Є—Б—Г—Ш–µ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞, –§–Я–Т - –њ–Њ–≤—А—И–Є–љ–∞ –Є—Б–њ–Њ–і –ї–Є–љ–Є—Ш–µ –Ю–Ґ–§ –≥—А–∞—Д–∞ –Ј–∞ —А–∞–Ј–Љ–∞—В—А–∞–љ—Г –§–®–Ґ, —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –њ–Њ–≤—А—И–Є–љ—Г –Є—Б–њ–Њ–і –ї–Є–љ—Ш–µ –≥—А–∞—Д–∞ –Ј–∞ –§–®–Ґ —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —Б—А–∞–Ј–Љ–µ—А–љ–∞ —Ш–µ –°—В—А–µ–ї —А–∞—Ж–Є—Г.
–£ —Б–ї—Г—З–∞—Ш—Г —А–∞–і–Є—Ш–∞–ї–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–љ–µ –§–®–Ґ, –Њ–≤–∞—Ш —А–∞—Ж–Є–Њ –њ–Њ–≤—А—И–Є–љ–∞ —Ш–µ –Є—Б—В–Є –Ј–∞ –±–Є–ї–Њ –Ї–Њ—Ш–Є –њ—А–µ—Б–µ–Ї –§–Ю–Я (—В—Ш. –§–Я–Т), –Є –±–Є–ї–Њ –Ї–Њ—Ш–Є –њ—А–µ—Б–µ–Ї –і–∞—Ш–µ —В–∞—З–∞–љ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞ –Ј–∞ —Ж–µ–ї—Г –§–Ю–Я. –£ —Б–ї—Г—З–∞—Ш—Г –∞—Б–Є–Љ–µ—В—А–Є—З–љ–µ –§–®–Ґ, —А–∞—Ж–Є–Њ —Б–µ –Љ–µ—Ъ–∞ —Б–∞ –њ—А–µ—Б–µ–Ї–Њ–Љ, –Љ–Њ–≥—Г—Ы–µ –Ј–љ–∞—В–љ–Њ. –£ –Њ–≤–Њ–Љ –і—А—Г–≥–Њ–Љ —Б–ї—Г—З–∞—Ш—Г, –љ–Є–≤–Њ –Ї–∞–Ї–≤–Њ—Ы–µ —Б–ї–Є–Ї–µ —Ш–µ –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ –њ—А–Њ—Б–µ—З–љ–Є–Љ –Њ–і–љ–Њ—Б–Њ–Љ –Њ–≤–µ –і–≤–µ –њ–Њ–≤—А—И–Є–љ–µ, —В—Ш. –њ—А–Њ—Б–µ—З–љ–Є–Љ –°—В—А–µ–ї —А–∞—Ж–Є–Њ–Љ –Ј–∞ —Б–≤–µ –§–Ю–Я –њ—А–µ—Б–µ–Ї–µ.
–§—Г–љ–Ї—Ж–Є—Ш–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ —Г —И–Є—А–µ–Љ –Њ–Ї–≤–Є—А—Г
–Ф–∞ –±–Є —Б–µ —А–∞–Ј—Г–Љ–µ–ї–∞ –њ—А–Є—А–Њ–і–∞ –§–Ю–Я, –љ–µ–Њ–њ—Е–Њ–і–љ–Њ —Ш–µ —Б–∞–≥–ї–µ–і–∞—В–Є –љ–∞ –Ї–Њ—Ш–Є –љ–∞—З–Є–љ —Ш–µ –њ–Њ–≤–µ–Ј–∞–љ–∞ —Б–∞ –љ–∞—Ш–±–Є—В–љ–Є—Ш–Є–Љ –Њ–њ—В–Є—З–Ї–Є–Љ –њ–Њ—Ш–Љ–Њ–≤–Є–Љ–∞. –Ъ–Њ–љ–Ї—А–µ—В–љ–Њ, —Б–∞ –Њ–±—Ш–µ–Ї—В–Њ–Љ –Є —Ъ–µ–≥–Њ–≤–Њ–Љ —Д–Є–Ј–Є—З–Ї–Њ–Љ —Б–ї–Є–Ї–Њ–Љ, –Ї–Њ—Ш–∞ —Ш–µ —Б–∞—З–Є—Ъ–µ–љ–∞ –Њ–і —Д–Є–Ј–Є—З–Ї–Є—Е —Б–ї–Є–Ї–∞ —В–∞—З–Ї–Є –Њ–±—Ш–µ–Ї—В–∞ - –Њ–њ–Є—Б–∞–љ–Є—Е —Б–∞ –§–®–Ґ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ - —Б–∞ –њ–Њ—Щ–µ–Љ —Б–≤–µ—В–ї–Њ—Б–љ–Њ–≥ –Ј—А–∞—З–µ—Ъ–∞ –Є —Б–∞ —Д—Г–љ–Ї—Ж–Є—Ш–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞ –Ї–Њ—Ш–µ –њ—А–Њ–Є–Ј–≤–Њ–і–µ –§–®–Ґ.
 –°–Ы–Ш–Ъ–Р 7: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р, –®–Ш–†–Ш –Ю–Ъ–Т–Ш–†
–°–Ы–Ш–Ъ–Р 7: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р, –®–Ш–†–Ш –Ю–Ъ–Т–Ш–†
–®–µ–Љ–∞ –љ–∞ —Б–ї–Є—Ж–Є –і–µ—Б–љ–Њ –њ–Њ–Ї–∞–Ј—Г—Ш–µ –і–∞ —Ш–µ –љ–∞—Ш–±–Є—В–љ–Є—Ш–µ —Б–≤–Њ—Ш—Б—В–≤–Њ –§–Ю–Я —Г –Њ–≤–Њ–Љ –Њ–Ї–≤–Є—А—Г —В–Њ —И—В–Њ –њ—А–Є–њ–∞–і–∞ –і–Њ–Љ–µ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є (—Д—А–µ–Ї–≤–µ–љ—Ж–Є—Ш–µ), –Ј–∞ —А–∞–Ј–ї–Є–Ї—Г –Њ–і –Њ–±—Ш–µ–Ї—В–∞, –§–®–Ґ –Є –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ, –Ї–Њ—Ш–Є –њ—А–Є–њ–∞–і–∞—Ш—Г –њ—А–Њ—Б—В–Њ—А–љ–Њ–Љ –і–Њ–Љ–µ–љ—Г. –§–Ю–Я —Ш–µ —А–∞—Ж–Є–Њ –≤–Є—Б–Є–љ–µ –њ—А–µ—Б–ї–Є–Ї–∞–љ–Њ–≥ —Б–Є–љ—Г—Б–Њ–Є–і–∞ –Є –≤–Є—Б–Є–љ–µ –Њ–±—Ш–µ–Ї—В–∞-—Б–Є–љ—Г—Б–Њ–Є–і–∞, –≥–і–µ —Б—Г –Њ–±–µ –њ—А–µ–і—Б—В–∞–≤—Щ–µ–љ–µ —Б–њ–µ–Ї—В—А—Г–Љ–Њ–Љ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Њ–≤–∞ –і–≤–∞ —Б–Є–љ—Г—Б–Њ–Є–і–∞.
–Я—А–Њ—Ж–µ—Б —Г –Ї–Њ–Љ —Б–µ —Г –і–Њ–Љ–µ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –њ—А–µ–Ї–Њ –§–Ю–Я –Є–Ј —Б–њ–µ–Ї—В—А—Г–Љ–∞ –Њ–і—А–µ—Т–µ–љ–Њ–≥ —Б–≤–Њ—Ш—Б—В–≤–Є–Љ–∞ —Б–Є–љ—Г—Б–Њ–Є–і–∞-–Њ–±—Ш–µ–Ї—В–∞ –і–Њ–±–Є—Ш–∞ —Б–њ–µ–Ї—В—А—Г–Љ —Б–ї–Є–Ї–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞, –Ї–Њ—Ш–Є –Њ–і—А–µ—Т—Г—Ш–µ —Б–≤–Њ—Ш—Б—В–≤–∞ –Њ–≤–µ —Б–ї–Є–Ї–µ, —Ш–µ –њ–∞—А–∞–ї–µ–ї–∞–љ –њ—А–Њ—Ж–µ—Б—Г –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–µ —Б–Є–љ—Г—Б–Њ–Є–і–∞-–Њ–±—Ш–µ–Ї—В–∞ –Є –§–®–Ґ —Г –њ—А–Њ—Б—В–Њ—А–љ–Њ–Љ –і–Њ–Љ–µ–љ—Г, –Ї–Њ—Ш–Є –љ–µ–њ–Њ—Б—А–µ–і–љ–Њ –њ—А–Њ–Є–Ј–≤–Њ–і–Є —Б–ї–Є–Ї—Г —Б–Є–љ—Г—Б–Њ–Є–і–∞. –Ф—А—Г–≥–Є–Љ —А–µ—З–Є–Љ–∞, –Њ–±–∞ –њ—А–Є—Б—В—Г–њ–∞ –і–∞—Ш—Г –Є—Б—В–Є —А–µ–Ј—Г–ї—В–∞—В. –Я—А–µ–і–љ–Њ—Б—В –Ї–Њ—А–Є—И—Ы–µ—Ъ–∞ —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞ —Ш–µ —Г —В–Њ–Љ–µ —И—В–Њ —Ш–µ –њ—А–Њ—Ж–µ—Б –Љ–љ–Њ–ґ–µ—Ъ–∞ —Б–њ–µ–Ї—В—А—Г–Љ–∞ —Ш–µ–і–љ–Њ—Б—В–∞–≤–љ–Є—Ш–Є –Њ–і –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–µ, –њ–Њ—Б–µ–±–љ–Њ —Г —Б–ї—Г—З–∞—Ш–µ–≤–Є–Љ–∞ –Ї–∞–і —Б—Г —Б–≤–Њ—Ш—Б—В–≤–∞ —Б–ї–Є–Ї–µ —А–µ–Ј—Г–ї—В–∞—В –≤–Є—И–µ –µ–ї–µ–Љ–µ–љ–∞—В–∞ –Ј–∞ –Ї–Њ—Ш–µ —Б–µ –њ—А–Њ—А–∞—З—Г–љ –≤—А—И–Є –Њ–і–≤–Њ—Ш–µ–љ–Њ.
–®–µ–Љ–∞ –њ–Њ—З–Є—Ъ–µ —Б–∞ —Б–∞–≤—А—И–µ–љ–Є–Љ –Њ–њ—В–Є—З–Ї–Є–Љ –Њ—В–≤–Њ—А–Њ–Љ, –∞–ї–Є —Ш–µ —Г –Њ—Б–љ–Њ–≤–Є –љ–µ–њ—А–Њ–Љ–µ—Ъ–µ–љ–∞ –Є –Ј–∞ –Њ–њ—В–Є—З–Ї–µ –Њ—В–≤–Њ—А–µ —Б–∞ –∞–±–µ—А–∞—Ж–Є—Ш–∞–Љ–∞ –Є/–Є–ї–Є –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ—Б—В–Є–Љ–∞ —Г –њ—А–µ–љ–Њ—Б—Г –∞–Љ–њ–ї–Є—В—Г–і–µ. –£ —В–Њ–Љ —Б–ї—Г—З–∞—Ш—Г —Б–µ –Љ–µ—Ъ–∞ –њ–Њ—Щ–µ —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г, —В—Ш. —Д—Г–љ–Ї—Ж–Є—Ш–∞ —И–Є—А–µ—Ъ–∞ –∞–Љ–њ–ї–Є—В—Г–і–µ, —И—В–Њ –і–Њ–≤–Њ–і–Є –і–Њ –њ—А–Њ–Љ–µ–љ–µ —Г –§–®–Ґ –Є —Ъ–µ–љ–Њ–Љ –§—Г—А–Є—Ш–µ–Њ–≤–Њ–Љ –њ–∞—А—Г, –§–Ю–Я. –Я—А–Њ–Љ–µ–љ–∞ –§–Ю–Я –љ–µ–њ–Њ—Б—А–µ–і–љ–Њ –Њ–і—А–µ—Т—Г—Ш–µ –њ—А–Њ–Љ–µ–љ—Г —Б–≤–Њ—Ш—Б—В–≤–∞ —Б–ї–Є–Ї–µ.
–Т–Є—И–µ–±–Њ—Ш–љ–∞ (–њ–Њ–ї–Є—Е—А–Њ–Љ–∞—В—Б–Ї–∞) –Є —Ш–µ–і–љ–Њ–±–Њ—Ш–љ–∞ (–Љ–Њ–љ–Њ—Е—А–Њ–Љ–∞—В—Б–Ї–∞) –§–Ю–Я/–§–Я–Т
–° –Њ–±–Ј–Є—А–Њ–Љ –љ–∞ —В–Њ –і–∞ –§–Ю–Я –Њ–њ–Є—Б—Г—Ш–µ —Д–Є–Ј–Є—З–Ї—Г —Б–ї–Є–Ї—Г —Б—В–≤–Њ—А–µ–љ—Г –Ї–Њ–љ–≤–Њ–ї—Г—Ж–Є—Ш–Њ–Љ –У–∞—Г—Б–Њ–≤—Б–Ї–µ —Б–ї–Є–Ї–µ –Є —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ (–§–®–Ґ) –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —Ъ–µ–љ —А–µ–Ј—Г–ї—В–∞—В —Б–µ –Љ–µ—Ъ–∞ —Б–∞ –≤–µ–ї–Є—З–Є–љ–Њ–Љ –§–®–Ґ, —В—Ш. —Б–∞ —В–∞–ї–∞—Б–љ–Њ–Љ –і—Г–ґ–Є–љ–Њ–Љ —Б–≤–µ—В–ї–Њ—Б—В–Є. –£ –љ–∞—З–µ–ї—Г, –Ї—А–∞—Ы–µ —В–∞–ї–∞—Б–љ–µ –і—Г–ґ–Є–љ–µ, –Ј–∞ –Ї–Њ—Ш–µ —Ш–µ –§–®–Ґ –Љ–∞—Ъ–∞, –Є–Љ–∞—Ш—Г –±–Њ—Щ–Є –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞, –Є –≤–Є—И—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В —А–µ–Ј–∞ –Њ–і –і—Г–ґ–Є—Е.
 –°–Ы–Ш–Ъ–Р 8: –Т–Ш–®–Х–С–Ю–И–Э–Р (–Я–Ю–Ы–Ш–•–†–Ю–Ь–Р–Ґ–°–Ъ–Р) –Ш –И–Х–Ф–Э–Ю–С–Ю–И–Э–Х (–Ь–Ю–Э–Ю–•–†–Ю–Ь–Р–Ґ–°–Ъ–Х) –§–Ю–Я/–§–Я–Т
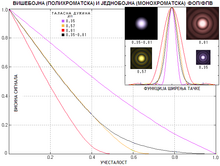
–°–Ы–Ш–Ъ–Р 8: –Т–Ш–®–Х–С–Ю–И–Э–Р (–Я–Ю–Ы–Ш–•–†–Ю–Ь–Р–Ґ–°–Ъ–Р) –Ш –И–Х–Ф–Э–Ю–С–Ю–И–Э–Х (–Ь–Ю–Э–Ю–•–†–Ю–Ь–Р–Ґ–°–Ъ–Х) –§–Ю–Я/–§–Я–Т –°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ–Њ–Ї–∞–Ј—Г—Ш–µ —А–∞–Ј–ї–Є–Ї—Г –Є–Ј–Љ–µ—Т—Г –§–Ю–Я (–Ї–∞–Њ —Ъ–µ–љ—Г –≤–µ–ї–Є—З–Є–љ—Г, –Є–Ј—А–∞–ґ–µ–љ—Г —Д—Г–љ–Ї—Ж–Є—Ш–Њ–Љ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞) –Ј–∞ –≤–Є—И–µ–±–Њ—Ш–љ—Г (–њ–Њ–ї–Є—Е—А–Њ–Љ–∞—В—Б–Ї—Г) —Б–≤–µ—В–ї–Њ—Б—В —Г —А–∞—Б–њ–Њ–љ—Г 0.35 –і–Њ 0.81 –Љ–Є–Ї—А–Њ–љ–∞ (350 –і–Њ 810 –љ–∞–љ–Њ–Љ–µ—В–∞—А–∞), —Б–∞ —Ш–µ–і–љ–µ, –Є –Ј–∞ —Ш–µ–і–љ–Њ–±–Њ—Ш–љ–µ —Б–≤–µ—В–ї–Њ—Б—В–Є —Б–∞ –њ–Њ—З–µ—В–Ї–∞, –Ї—А–∞—Ш–∞, –Є –њ—А–Є–±–ї–Є–ґ–љ–Њ –Є–Ј —Б—А–µ–і–Є–љ–µ –Њ–≤–Њ–≥ —Б–њ–µ–Ї—В—А–∞–ї–љ–Њ–≥ —А–∞—Б–њ–Њ–љ–∞, —Б–∞ –і—А—Г–≥–µ —Б—В—А–∞–љ–µ (–Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А).
–Т–Є—И–µ–±–Њ—Ш–љ–∞ –§–Ю–Я —Ш–µ –Ј–∞ —Г—Ш–µ–і–љ–∞—З–µ–љ—Г –Њ—Б–µ—В—Щ–Є–≤–Њ—Б—В –і–µ—В–µ–Ї—В–Њ—А–∞; –Ј–∞ —Д–Њ—В–Њ–њ—Б–Ї–Њ –Њ–Ї–Њ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Ш–µ –Є—Б—В–Є –і–Њ —Б—А–µ–і–Є—И—Ъ–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Є –±–ї–∞–≥–Њ –љ–Є–ґ–Є –њ—А–µ–Љ–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —А–µ–Ј–∞.
–£ –і–µ—Б–љ–Њ–Љ –≥–Њ—А—Ъ–µ–Љ —Г–≥–ї—Г —Б—Г –њ—А–Є–Ї–∞–Ј–∞–љ–µ —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ –Ј–∞ –Њ–≤–µ —В–∞–ї–∞—Б–љ–µ –і—Г–ґ–Є–љ–µ, –Ї–∞–Њ –≥—А–∞—Д–Є–Ї–Њ–љ–Є —А–∞—Б–њ–Њ—А–µ–і–∞ –µ–љ–µ—А–≥–Є—Ш–µ, –Є –Ї–∞–Њ —Д–Є–Ј–Є—З–Ї–µ —Б–ї–Є–Ї–µ.
–£ –љ–∞—З–µ–ї—Г, —Г—З–µ—Б—В–∞–ї–Њ—Б—В —А–µ–Ј–∞, –љ–∞ –Ї–Њ—Ш–Њ—Ш –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞ –њ–∞–і–∞ –љ–∞ –љ—Г–ї—Г, —Ш–µ –Ј–∞ —Б–≤–µ—В–ї–Њ—Б—В —Г —И–Є—А–µ–Љ —Б–њ–µ–Ї—В—А–∞–ї–љ–Њ–Љ —А–∞—Б–њ–Њ–љ—Г, —В—Ш. –Ј–∞ –≤–Є—И–µ–±–Њ—Ш–љ—Г —Б–≤–µ—В–ї–Њ—Б—В, –≤–Є—И–∞ –Њ–і —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –љ–∞—Ш–і—Г–ґ–µ, –Є –љ–Є–ґ–∞ –Њ–і —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –љ–∞—Ш–Ї—А–∞—Ы–µ —В–∞–ї–∞—Б–љ–µ –і—Г–ґ–Є–љ–µ —Г —А–∞—Б–њ–Њ–љ—Г. –Я—А–Є —Г—Ш–µ–і–љ–∞—З–µ–љ–Њ—Ш —Б–њ–µ–Ї—В—А–∞–ї–љ–Њ—Ш –Њ—Б–µ—В—Щ–Є–≤–Њ—Б—В–Є, –Њ–љ–∞ —Ш–µ —Г —Б—А–µ–і–Є–љ–Є –Є–Ј–Љ–µ—Т—Г –Њ–≤–µ –і–≤–µ. –£—З–µ—Б—В–∞–ї–Њ—Б—В —А–µ–Ј–∞ –Ј–∞ —Ш–µ–і–љ–Њ–±–Њ—Ш–љ—Г —Б–≤–µ—В–ї–Њ—Б—В —Ш–µ –Њ–±—А–љ—Г—В–Њ —Б—А–∞–Ј–Љ–µ—А–љ–∞ —В–∞–ї–∞—Б–љ–Њ—Ш –і—Г–ґ–Є–љ–Є - —В–Њ –≤–Є—И–∞ —И—В–Њ —Ш–µ —В–∞–ї–∞—Б–љ–∞ –і—Г–ґ–Є–љ–∞ –Ї—А–∞—Ы–∞.
–Я—А–Є–Љ–µ—А–Є —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞
–Ь–∞–і–∞ –§–Ю–Я –Љ–Њ–ґ–µ –і–∞ —Б–µ –Ї–Њ—А–Є—Б—В–Є –Ј–∞ —Г—В–≤—А—Т–Є–≤–∞—Ъ–µ –µ—Д–µ–Ї—В–∞ –љ–∞—Ш—А–∞–Ј–ї–Є—З–Є—В–Є—Ш–Є—Е —З–Є–љ–Є–ї–∞—Ж–∞ –љ–∞ —Б–≤–Њ—Ш—Б—В–≤–∞ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ, —Г–Њ–±–Є—З–∞—Ш–µ–љ–Њ —Ш–µ –і–∞ —Б–µ –Ї–Њ—А–Є—Б—В–Є –Ј–∞ –њ—А–Њ—Ж–µ–љ—Г –µ—Д–µ–Ї—В–∞ –Њ–њ—В–Є—З–Ї–Є—Е –∞–±–µ—А–∞—Ж–Є—Ш–∞, –±–Є–ї–Њ —Г —В–Њ–Ї—Г —Б—В–≤–∞—А–∞—Ъ–∞ –Њ–њ—В–Є—З–Ї–Є—Е —Б–Ї–ї–Њ–њ–Њ–≤–∞, –Є–ї–Є –і–∞ –±–Є —Б–µ —Б–≤–Њ—Ш—Б—В–≤–∞ –Є—Б—В–Є—Е –њ—А–Є–Ї–∞–Ј–∞–ї–∞ —Г —Г—Я–±–µ–љ–Є—Ж–Є–Љ–∞ –Є –њ—Г–±–ї–Є–Ї–∞—Ж–Є—Ш–∞–Љ–∞. –£–Ј –µ—Д–µ–Ї–∞—В –∞–±–µ—А–∞—Ж–Є—Ш–∞, —В–∞–Ї–Њ—Т–µ —Б–µ –Ї–Њ—А–Є—Б—В–Є –і–∞ –њ–Њ–Ї–∞–ґ–µ —Г—В–Є—Ж–∞—Ш –Ј–∞–Ї–ї–Њ–љ–∞ —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г –љ–∞ –Ї–∞–Ї–≤–Њ—Ы—Г —Б–ї–Є–Ї–µ.
–£ —Б–ї—Г—З–∞—Ш—Г –љ–Є—Б–Ї–Њ–≥ –љ–Є–≤–Њ–∞ –∞–±–µ—А–∞—Ж–Є—Ш–∞, –љ–∞—Ш—З–µ—И—Ы–µ —Б–µ –Ї–Њ—А–Є—Б—В–Є —Б–∞–Љ–Њ –і–µ–Њ –§–Ю–Я –Ї–Њ—Ш–Є –њ—А–Є–Ї–∞–Ј—Г—Ш–µ –∞–њ—Б–Њ–ї—Г—В–љ—Г –≤–µ–ї–Є—З–Є–љ—Г –њ—А–µ–љ–Њ—Б–∞ –Њ—И—В—А–Є–љ–µ —Б–ї–Є–Ї–µ, —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ (–§–Я–Т). –Ч–∞ –≤–Є—Б–Њ–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞, –§–Ю–Я –Љ–Њ–ґ–µ –і–∞—В–Є –њ–Њ—В–њ—Г–љ–Є—Ш–Є —Г–≤–Є–і —Г —Б–≤–Њ—Ш—Б—В–≤–∞ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ.
–Э–Є–Ј–∞–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞
 –°–Ы–Ш–Ъ–Р 9: –Я—А–Є–Љ–µ—А–Є —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ј–∞ –љ–Є–Ј–∞–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞
–°–Ы–Ш–Ъ–Р 9: –Я—А–Є–Љ–µ—А–Є —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ј–∞ –љ–Є–Ј–∞–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞
–Я—А–Є–Љ–µ—А–Є –і–µ—Б–љ–Њ —Б—Г –≥—А–∞—Д–Є–Ї–Њ–љ–Є –§–Ю–Я –Ї–∞–Ї–Њ —Б–µ –љ–∞—Ш—З–µ—И—Ы–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞—Ш—Г: –њ—А–µ–љ–Њ—Б –Њ—И—В—А–Є–љ–µ —Б–ї–Є–Ї–µ —Ш–µ –і–∞—В –Ј–∞ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А –Ї–Њ—Ш–Є —Б–µ —А–∞–Ј–Љ–∞—В—А–∞ (—Ж—А–≤–µ–љ–∞ –ї–Є–љ–Є—Ш–∞) –Є, —А–∞–і–Є –њ–Њ—А–µ—Т–µ—Ъ–∞, –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А (—Ж—А–љ–∞ –ї–Є–љ–Є—Ш–∞). –£ –љ–∞—З–µ–ї—Г, —И—В–Њ —Ш–µ –ї–Є–љ–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞ –љ–Є–ґ–µ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –ї–Є–љ–Є—Ш—Г –њ—А–µ–љ–Њ—Б–∞ —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —В–Њ —Ш–µ –љ–Є–ґ–∞ –Є –Њ—И—В—А–Є–љ–∞ —Ъ–µ–≥–Њ–≤–µ —Б–ї–Є–Ї–µ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –љ–∞—Ш–≤–µ—Ы—Г –Љ–Њ–≥—Г—Ы—Г.
–£–Ј —Б–≤–∞–Ї–Є –≥—А–∞—Д –і–∞—В–∞ —Ш–µ –Є –Њ–і–≥–Њ–≤–∞—А–∞—Ш—Г—Ы–∞ —Д—Г–љ–Ї—Ж–Є—Ш–∞ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ (–§–®–Ґ), —В—Ш. —Д–Є–Ј–Є—З–Ї–∞ —Б–ї–Є–Ї–∞ —В–∞—З–Ї–µ –Ї–∞–Ї–≤—Г —Б—В–≤–∞—А–∞ —В–∞—Ш –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А. –£ —Б–ї—Г—З–∞—Ш—Г —Б—А–µ–і–Є—И—Ъ–µ–≥ –Ј–∞–Ї–ї–Њ–љ–∞ —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г, –Њ—И—В—А–Є–љ–∞ —Б–ї–Є–Ї–µ –љ–∞ –і–µ—Б–љ–Њ—Ш —Б—В—А–∞–љ–Є –≥—А–∞—Д–∞ —Ш–µ –≤–Є—И–∞ –љ–µ–≥–Њ –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А - —В–Њ –≤–Є—И–µ —И—В–Њ —Ш–µ –≤–µ—Ы–Є –Ј–∞–Ї–ї–Њ–љ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А - —Ш–µ—А –∞–љ—Г–ї–∞—А–љ–Є –Њ—В–≤–Њ—А –њ—А–Њ–Є–Ј–≤–Њ–і–Є –Љ–∞—Ъ–Є —Б—А–µ–і–Є—И—Ъ–Є –≤—А—Е —Г —Б–ї–Є—Ж–Є —В–∞—З–Ї–µ.
–Я–Њ—Б–ї–µ–і–Є—Ж–µ —Б—А–µ–і–Є—И—Ъ–µ–≥ –Ј–∞–Ї–ї–Њ–љ–∞ –љ–∞ –Њ–њ—В–Є—З–Ї—Г —Б–ї–Є–Ї—Г (–≥–Њ—А–µ –і–µ—Б–љ–Њ) –њ—А–Є–Ї–∞–Ј–∞–љ–µ —Б—Г –Ј–∞ —В—А–Є –≤–µ–ї–Є—З–Є–љ–µ –Ј–∞–Ї–ї–Њ–љ–∞, 0.2D, 0.33D –Є 0.5D, –≥–і–µ —Ш–µ D –њ—А–µ—З–љ–Є–Ї –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞. –І–µ—В–Є—А–Є –Ї–ї–∞—Б–Є—З–љ–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ (–Є—Б–њ–Њ–і) —Б—Г –љ–∞ –љ–Є–≤–Њ—Г —В–Ј–≤. –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–µ –≥—А–∞–љ–Є—Ж–µ, 0.074ќї –†–Ь–°. –Э–Є –∞–±–µ—А–∞—Ж–Є—Ш–µ, –љ–Є –Ј–∞–Ї–ї–Њ–љ–Є –љ–µ –і–Њ–≤–Њ–і–µ –і–Њ –њ—А–Њ–Љ–µ–љ–∞ —Г –Њ–±–ї–Є–Ї—Г —Б–ї–Є–Ї–µ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –Њ–±—Ш–µ–Ї—В. –И–µ–і–Є–љ–∞ –њ–Њ—Б–ї–µ–і–Є—Ж–∞ —Ш–µ, —Г–Њ–њ—И—В–µ–љ–Њ, –љ–µ—И—В–Њ —Б–ї–∞–±–Є—Ш–∞ –Њ—И—В—А–Є–љ–∞ —Б–ї–Є–Ї–µ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –Њ—И—В—А–Є–љ—Г —Г —Б–∞–≤—А—И–µ–љ–Њ–Љ –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г.
–Ч–∞ –Њ–≤–∞—Ш, —Б—А–∞–Ј–Љ–µ—А–љ–Њ –Љ–∞–ї–Є –љ–Є–≤–Њ –њ–∞–і–∞ –њ—А–µ–љ–Њ—Б–∞ –Њ—И—В—А–Є–љ–µ —Б–ї–Є–Ї–µ, –љ–µ–Љ–∞ –±–Є—В–љ–µ —А–∞–Ј–ї–Є–Ї–µ –Є–Ј–Љ–µ—Т—Г —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞, –§–Ю–Я, –Є —Ш–µ–і–љ–Њ–≥ –Њ–і —Ъ–µ–љ–∞ –і–≤–∞ —Б–∞—Б—В–∞–≤–љ–∞ –і–µ–ї–∞, —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ (—Б–Є–≥–љ–∞–ї–∞), –§–Я–Т. –Ч–∞—В–Њ —Б–µ –Њ–≤–∞—Ш –≥—А–∞—Д –љ–∞—Ш—З–µ—И—Ы–µ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –Ї–∞–Њ –≥—А–∞—Д —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ, –§–Я–Т (–µ–љ–≥. Modulation transfer function, MTF).
–Т–Є—Б–Њ–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞
 –°–Ы–Ш–Ъ–Р 10: –Я—А–Є–Љ–µ—А–Є —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ј–∞ –≤–Є—Б–Њ–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞
–°–Ы–Ш–Ъ–Р 10: –Я—А–Є–Љ–µ—А–Є —Д—Г–љ–Ї—Ж–Є—Ш–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Ј–∞ –≤–Є—Б–Њ–Ї –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞ –И–µ–і–Є–љ–∞ —А–∞–Ј–ї–Є–Ї–∞ –Є–Ј–Љ–µ—Т—Г –§–Ю–Я –Є –§–Я–Т –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ–Њ—Ш–∞–≤–Є –Ї–∞–і —Б—Г –∞–±–µ—А–∞—Ж–Є—Ш–µ –≤–µ–ї–Є–Ї–µ, —Г –Ї–Њ–Љ —Б–ї—Г—З–∞—Ш—Г –ї–Є–љ–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ –њ–∞–і–∞ –±–ї–Є–Ј—Г –љ—Г–ї–µ, –Є —Г–Ї–Њ–ї–Є–Ї–Њ —Б–µ —Д–∞–Ј–љ–∞ —А–∞–Ј–ї–Є–Ї–∞ –њ—А–Њ–Љ–µ–љ–Є —Б–∞ 0 –љ–∞ ѕА, –њ—А–Њ–Љ–µ–љ–∞ —Д–∞–Ј–µ –Љ–µ—Ъ–∞ –Ј–љ–∞–Ї –§–Ю–Я –Є –Њ–љ–∞ –њ–Њ–Ї–∞–Ј—Г—Ш–µ –љ–µ–≥–∞—В–Є–≤–∞–љ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ, —В—Ш. –ї–Є–љ–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ —Б–µ —Б–њ—Г—И—В–∞ –Є—Б–њ–Њ–і –≤–Њ–і–Њ—А–∞–≤–љ–µ —Б–Ї–∞–ї–µ –≥—А–∞—Д–∞. –Ю–≤–Њ —Г–Ї–∞–Ј—Г—Ш–µ –љ–∞ —В–Ј–≤. –Њ–±—А–љ—Г—В –Ї–Њ–љ—В—А–∞—Б—В, —В—Ш. —Б–≤–µ—В–ї–µ –њ–Њ–≤—А—И–Є–љ–µ –љ–∞ –Њ–±—Ш–µ–Ї—В—Г –њ–Њ—Б—В–∞—Ш—Г —В–∞–Љ–љ–µ —Г —Ъ–µ–≥–Њ–≤–Њ—Ш —Б–ї–Є—Ж–Є, –∞ —В–∞–Љ–љ–µ –њ–Њ—Б—В–∞—Ш—Г —Б–≤–µ—В–ї–µ. –Я–Њ—И—В–Њ —Ш–µ –§–Я–Т —Ш–µ–і–љ–∞–Ї–∞ –∞–њ—Б–Њ–ї—Г—В–љo—Ш –≤—А–µ–і–љ–Њ—Б—В–Є –§–Ю–Я, –Њ–љ–∞ –Є –Њ–≤–∞—Ш –і–µ–Њ –њ—А–µ–љ–Њ—Б–∞ –њ–Њ–Ї–∞–Ј—Г—Ш–µ —Г –њ–Њ–Ј–Є—В–Є–≤–љ–Њ–Љ –і–µ–ї—Г –≥—А–∞—Д–∞, —В—Ш. –љ–µ —Г–Ї–∞–Ј—Г—Ш–µ –љ–∞ –Њ–±—А–љ—Г—В–Є –Ї–Њ–љ—В—А–∞—Б—В.
–Э–∞ —Б–ї–Є—Ж–Є –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј–∞–љ–µ —Б—Г –њ–Њ—Б–ї–µ–і–Є—Ж–µ –≤–Є—Б–Њ–Ї–Њ–≥ –љ–Є–≤–Њ–∞ —З–µ—В–Є—А–Є –Ї–ї–∞—Б–Є—З–љ–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ –љ–∞ —Б–ї–Є–Ї—Г –°–Є–Љ–µ–љ—Б–Њ–≤–µ –Ј–≤–µ–Ј–і–µ (–µ–љ–≥. Siemens star), —Ш–µ–і–љ–Њ–≥ –Њ–і —Г–Њ–±–Є—З–∞—Ш–µ–љ–Є—Е –Њ–±—Ш–µ–Ї–∞—В–∞ –Ј–∞ —В–µ—Б—В–Є—А–∞—Ъ–µ –Њ–њ—В–Є–Ї–µ (—Б–ї–Є–Ї–∞ —Ш–µ —Г–≤–µ—Ы–∞–љ–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –Њ–±—Ш–µ–Ї—В –Ј–±–Њ–≥ —Ш–∞—Б–љ–Њ—Ы–µ). –Р–±–µ—А–∞—Ж–Є—Ш–µ —Б—Г —Б–ї–Є—З–љ–µ –≤–µ–ї–Є—З–Є–љ–µ, –љ–∞ –љ–Є–≤–Њ—Г 0.5ќї –†–Ь–°, –∞ —А–∞–Ј–ї–Є–Ї–∞ —Г –Т-–Ф (–≤—А—Е-–і–љ–Њ) –≥—А–µ—И–Ї–∞ —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞ —Ш–µ –њ–Њ—Б–ї–µ–і–Є—Ж–∞ —А–∞–Ј–ї–Є—З–Є—В–Є—Е –Њ–±–ї–Є–Ї–∞ –Њ–і—Б—В—Г–њ–∞—Ъ–∞ –Њ–≤–Є—Е –∞–±–µ—А–∞—Ж–Є—Ш–∞ –Њ–і —Б–∞–≤—А—И–µ–љ–Њ–≥ —Б—Д–µ—А–љ–Њ–≥ –Њ–±–ї–Є–Ї–∞.
–Ю–±—А–љ—Г—В –Ї–Њ–љ—В—А–∞—Б—В —Ш–µ –њ—А–Є—Б—Г—В–∞–љ –Ї–Њ–і –і–µ—Д–Њ–Ї—Г—Б–∞, –∞—Б—В–Є–≥–Љ–∞—В–Є–Ј–Љ–∞ –Є –Ї–Њ–Љ–µ, –Ї–∞–Њ —И—В–Њ –§–Ю–Я –њ–Њ–Ї–∞–Ј—Г—Ш–µ, –і–Њ–Ї —Б–µ —В–Њ –љ–µ –≤–Є–і–Є –њ–Њ –ї–Є–љ–Є—Ш–Є –њ—А–µ–љ–Њ—Б–∞ –§–Я–Т. –Ю–≤–∞—Ш –љ–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞ —Ш–µ –Ј–љ–∞—В–љ–Њ –Є–Ј–љ–∞–і –і–Њ–Ј–≤–Њ—Щ–µ–љ–Њ–≥ –љ–Є–≤–Њ–∞ –Ј–∞ –∞—Б—В—А–Њ–љ–Њ–Љ—Б–Ї–µ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–µ, —В–µ –Њ–≤–∞—Ш –љ–µ–і–Њ—Б—В–∞—В–∞–Ї –§–Я–Т —Г –Њ–≤–Њ–Љ –њ–Њ—Щ—Г –љ–Є—Ш–µ –±–Є—В–∞–љ. –£ —Б–ї—Г—З–∞—Ш—Г —Д–Њ—В–Њ–≥—А–∞—Д—Б–Ї–Є—Е –Є–љ—Б—В—А—Г–Љ–µ–љ–∞—В–∞, –Љ–µ—Т—Г—В–Є–Љ, –∞–±–µ—А–∞—Ж–Є—Ш–µ —Б—Г, —Г–Њ–њ—И—В–µ–љ–Њ –≥–Њ–≤–Њ—А–µ—Ы–Є, –±–Є—В–љ–Њ –≤–µ—Ы–µ, –Є –§–Ю–Я —Ш–µ –±–Њ—Щ–Є –Є–Ј–±–Њ—А –Ї–∞–Њ –Љ–µ—А–∞ –Ї–∞–Ї–≤–Њ—Ы–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ.
–§–Ю–Я –Є CCD
–Ф–Њ–Ї —Б—Г –∞–±–µ—А–∞—Ж–Є—Ш–µ —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞ –Є –Ј–∞–Ї–ї–Њ–љ–Є —Г –Њ–њ—В–Є—З–Ї–Њ–Љ –Њ—В–≤–Њ—А—Г —З–Є–љ–Є–Њ—Ж–Є –Ї–Њ—Ш–Є —Г—В–Є—З—Г –љ–∞ –Њ—И—В—А–Є–љ—Г —Б–∞–Љ–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ, —Б–≤–Њ—Ш—Б—В–≤–∞ –і–µ—В–µ–Ї—В–Њ—А–∞ –Љ–Њ–≥—Г –і–Њ–і–∞—В–љ–Њ –і–∞ —Г—В–Є—З—Г –љ–∞ –Ї–∞–Ї–≤–Њ—Ы—Г –Ї–Њ–љ–∞—З–љ–µ —Б–ї–Є–Ї–µ. –£ —В–Њ–Љ –њ–Њ–≥–ї–µ–і—Г —Ш–µ –Њ–і –њ–Њ—Б–µ–±–љ–Њ–≥ –Ј–љ–∞—З–∞—Ш–∞ –Ї–∞–Ї–Њ –љ–∞ –Ї–Њ–љ—В—А–∞—Б—В –Ї–Њ–љ–∞—З–љ–µ —Б–ї–Є–Ї–µ —Г—В–Є—З–µ –≤–µ–ї–Є—З–љ–∞ CCD –њ–Є–Ї—Б–µ–ї–∞, —Ш–µ–і–Є–љ–Є—З–љ–Њ–≥ –Ї–≤–∞–і—А–∞—В–љ–Њ–≥ —Б–µ–љ–Ј–Њ—А–∞ –Њ–≤–µ —И–Є—А–Њ–Ї–Њ –Ї–Њ—А–Є—И—Ы–µ–љ–µ –≤—А—Б—В–µ –і–µ—В–µ–Ї—В–Њ—А–∞. –Я—А–µ–љ–Њ—Б –Њ—И—В—А–Є–љ–µ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ –љ–∞ –Ї–Њ–љ–∞—З–љ—Г —Б–ї–Є–Ї—Г –Њ–≤–і–µ –Ј–∞–≤–Є—Б–Є –Њ–і –≤–µ–ї–Є—З–Є–љ–µ –њ–Є–Ї—Б–µ–ї–∞ —Г –Њ–і–љ–Њ—Б—Г –љ–∞ –≤–µ–ї–Є—З–Є–љ—Г —Б—А–µ–і–Є—И—Ъ–µ–≥ –≤—А—Е–∞ —Д–Є–Ј–Є—З–Ї–µ —Б–ї–Є–Ї–µ —В–∞—З–Ї–µ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, —В—Ш. —Ъ–µ–≥–Њ–≤–µ —Д—Г–љ–Ї—Ж–Є—Ш–µ —И–Є—А–µ—Ъ–∞ —В–∞—З–Ї–µ.
–Р–Ї–Њ —Ш–µ –і—Г–ґ–Є–љ–∞ —Б—В—А–∞–љ–µ –њ–Є–Ї—Б–µ–ї–∞ p, —Г —Ш–µ–і–љ–Є—Ж–∞–Љ–∞ ќїF, —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –Ї–Њ–љ—В—А–∞—Б—В–∞, —В—Ш. –§–Ю–Я CCD –і–µ—В–µ–Ї—В–Њ—А–∞ –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А —Ш–µ –і–∞—В–∞ —Б–Є–љ–Ї —Д—Г–љ–Ї—Ж–Є—Ш–Њ–Љ:
- PCCD = sinc(ѕАpќљ) = sin(180pќљ)/ѕАpќљ ........ (7)
(–Ј–∞ ќљ=0 —Д—Г–љ–Ї—Ж–Є—Ш–∞ —Ш–µ –љ–µ–і–µ—Д–Є–љ–Є—Б–∞–љ–∞, –∞–ї–Є —В–µ–ґ–Є –Ї–∞ —Ш–µ–і–∞–љ, —И—В–Њ –њ—А–µ–і—Б—В–∞–≤—Щ–∞ —Ъ–µ–љ—Г –≥—А–∞–љ–Є—З–љ—Г –≤—А–µ–і–љ–Њ—Б—В).
–Я—А–µ–љ–Њ—Б –Ї–Њ–љ—В—А–∞—Б—В–∞ –Ї–Њ–љ–∞—З–љ–µ, CCD —Б–ї–Є–Ї–µ —Ш–µ, —Б–∞–≥–ї–∞—Б–љ–Њ –Њ–њ—И—В–µ–Љ –њ—А–∞–≤–Є–ї—Г –Ј–∞ —Д—Г–љ–Ї—Ж–Є—Ш—Г –њ—А–µ–љ–Њ—Б–∞, —Ш–µ–і–љ–∞–Ї –њ—А–Њ–Є–Ј–≤–Њ–і—Г –њ–Њ—Ш–µ–і–Є–љ–∞—З–љ–Є—Е –њ—А–µ–љ–Њ—Б–∞, —В—Ш. –њ—А–Њ–Є–Ј–≤–Њ–і—Г –§–Ю–Я –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞ –Є —Д—Г–љ–Ї—Ж–Є—Ш–µ –њ—А–µ–љ–Њ—Б–∞ CCD –і–µ—В–µ–Ї—В–Њ—А–∞:
- Pf = (PCCD)(–§–Ю–Я) ........ (8)
 –°–Ы–Ш–Ъ–Р 11: –Я–†–Х–Э–Ю–° –Ъ–Ю–Э–Ґ–†–Р–°–Ґ–Р –Ч–Р –Ъ–Ю–Э–Р–І–Э–£ CCD –°–Ы–Ш–Ъ–£
–°–Ы–Ш–Ъ–Р 11: –Я–†–Х–Э–Ю–° –Ъ–Ю–Э–Ґ–†–Р–°–Ґ–Р –Ч–Р –Ъ–Ю–Э–Р–І–Э–£ CCD –°–Ы–Ш–Ъ–£ –°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј—Г—Ш–µ –њ—А–µ–љ–Њ—Б –Ї–Њ–љ—В—А–∞—Б—В–∞ CCD –і–µ—В–µ–Ї—В–Њ—А–∞ –Ј–∞ –љ–µ–Ї–Њ–ї–Є–Ї–Њ –≤–µ–ї–Є—З–Є–љ–∞ –њ–Є–Ї—Б–µ–ї–∞ (–ї–µ–≤–Њ), –Є –њ—А–Њ–Є–Ј–≤–Њ–і –Њ–≤–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Є –§–Ю–Я —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ—В–≤–Њ—А–∞ (–і–µ—Б–љ–Њ, —Ж—А–љ–∞ –ї–Є–љ—Ш–∞ —Ш–µ –§–Ю–Я —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ—В–≤–Њ—А–∞). –Ч–∞ p=2, –љ–∞ –њ—А–Є–Љ–µ—А, —И—В–Њ –Ј–∞ f/5 —Б–Ї–ї–Њ–њ –Є ќї=0,5 –Љ–Є–Ї—А–Њ–љ–∞ –Њ–і–≥–Њ–≤–∞—А–∞ –њ–Є–Ї—Б–µ–ї—Г —Б–∞ —Б—В—А–∞–љ–Њ–Љ –Њ–і 5 –Љ–Є–Ї—А–Њ–љ–∞ (pќїF=5), –њ—А–µ–љ–Њ—Б –Ї–Њ–љ—В—А–∞—Б—В–∞ –њ–∞–і–∞ –љ–∞ –љ—Г–ї—Г –Ј–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В ќљ=0,5, –∞ –Ј–∞ –Њ—Б—В–∞—В–∞–Ї —А–∞—Б–њ–Њ–љ–∞ –і–Њ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —А–µ–Ј–∞ —Б–ї–Є–Ї–∞ –Є–Љ–∞ –Њ–±—А–љ—Г—В –Ї–Њ–љ—В—А–∞—Б—В.
–£–Ј —В–Њ, –Ї–∞–Њ —И—В–Њ –њ—А–Њ–Є–Ј–≤–Њ–і –Њ–≤–Њ–≥ –њ—А–µ–љ–Њ—Б–∞ –Є –§–Ю–Я —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ—В–≤–Њ—А–∞ –љ–∞ –і–µ—Б–љ–Њ—Ш —Б—В—А–∞–љ–Є –њ–Њ–Ї–∞–Ј—Г—Ш–µ, –њ—А–µ–љ–Њ—Б –Ї–Њ–љ—В—А–∞—Б—В–∞ –Ј–∞ –Њ–≤—Г –≤–µ–ї–Є—З–Є–љ—Г –њ–Є–Ї—Б–µ–ї–∞ —Ш–µ –љ–∞ –љ–Є–≤–Њ—Г –і–≤–∞ –њ—Г—В–∞ –Љ–∞—Ъ–µ–≥ –Њ—В–≤–Њ—А–∞ –і–Њ ќљ=0,5, –Є —Б–∞–Љ–Њ –Љ–∞–ї–Є –і–µ–Њ –њ—А–µ–љ–Њ—Б–∞ —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ—В–≤–Њ—А–∞ –Ј–∞ –Њ—Б—В–∞—В–∞–Ї —А–∞—Б–њ–Њ–љ–∞ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –і–Њ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —А–µ–Ј–∞. –Ф–∞ –±–Є —Б–µ –Є–Ј–±–µ–≥–∞–Њ –Њ–±—А–љ—Г—В–Є –Ї–Њ–љ—В—А–∞—Б—В, –њ–Њ—В—А–µ–±–∞–љ —Ш–µ –і–≤–∞ –њ—Г—В–∞ –Љ–∞—Ъ–Є –њ–Є–Ї—Б–µ–ї (p=1), –∞–ї–Є –і–∞ –±–Є –Ї–Њ–љ—В—А–∞—Б—В –Ї–Њ–љ–∞—З–љ–µ (CCD) —Б–ї–Є–Ї–µ –±–Є–Њ –±–ї–Є–Ј—Г –Ї–Њ–љ—В—А–∞—Б—В–∞ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ, –њ–Њ—В—А–µ–±–∞–љ —Ш–µ —З–µ—В–Є—А–Є –њ—Г—В–∞ –Љ–∞—Ъ–Є (p=0,5).
–Я–Њ –Э–∞–Є–Ї—Г–Є—Б—В–Њ–≤–Њ–Љ –њ—А–∞–≤–Є–ї—Г (–µ–љ–≥. Nyquist criterion, –Є–Ј–≤–Њ—А–љ–Њ —Г –Њ–Ї–≤–Є—А—Г –і–Є–≥–Є—В–∞–ї–љ–µ –і–µ—В–µ–Ї—Ж–Є—Ш–µ –∞–љ–∞–ї–Њ–≥–љ–Њ–≥ —Б–Є–≥–љ–∞–ї–∞, –љ–∞–≤–Њ–і–µ—Ы–Є –і–∞ —Ш–µ –Ј–∞ —В–∞—З–љ—Г –і–µ—В–µ–Ї—Ж–Є—Ш—Г –µ–ї–µ–Ї—В—А–Њ–љ—Б–Ї–Њ–≥ —Б–Є–≥–љ–∞–ї–∞ –љ–µ–Њ–њ—Е–Њ–і–љ–Њ –і–∞ —Ш–µ —Г—З–µ—Б—В–∞–ї–Њ—Б—В –і–µ—В–µ–Ї—В–Њ—А–∞ - –Њ–і—А–µ—Т–µ–љ–∞ –≤–µ–ї–Є—З–љ–Њ–Љ —Ъ–µ–≥–Њ–≤–µ —Ш–µ–і–Є–љ–Є—Ж–µ –і–µ—В–µ–Ї—Ж–Є—Ш–µ - –±–∞—А –і–≤–∞ –њ—Г—В–∞ –≤–µ—Ы–∞ –Њ–і —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —Б–Є–≥–љ–∞–ї–∞), –Њ–≤–∞ –њ–Њ—Б–ї–µ–і—Ъ–∞ –≤–µ–ї–Є—З–Є–љ–∞ –њ–Є–Ї—Б–µ–ї–∞ —Ш–µ –≥–Њ—А—Ъ–∞ –≥—А–∞–љ–Є—Ж–∞ –њ—А–Є –Ї–Њ—Ш–Њ—Ш —Б—Г –і–≤–∞ —В–∞—З–Ї–∞—Б—В–∞ –Є–Ј–≤–Њ—А–∞ —Б–≤–µ—В–ї–Њ—Б—В–Є –љ–∞ —А–∞—Б—В–Њ—Ш–∞—Ъ—Г –≥—А–∞–љ–Є—З–љ–µ –і–Є—Д—А–∞–Ї—Ж–Є–Њ–љ–µ —А–∞–Ј–і–≤–Њ—Ш–љ–µ –Љ–Њ—Ы–Є —Ш–∞—Б–љ–Њ —А–∞–Ј–і–≤–Њ—Ш–µ–љ–∞.
–Я–Њ—И—В–Њ —Ш–µ –њ—А–≤–∞ –љ—Г–ї–∞ —Б–Є–љ–Ї —Д—Г–љ–Ї—Ж–Є—Ш–µ —Г –њ—А–µ–љ–Њ—Б—Г –Ї–Њ–љ—В—А–∞—Б—В–∞ –Ј–∞ pќљ=1, –њ—А–≤–∞ –љ—Г–ї–∞ –њ—А–Њ–Є–Ј–≤–Њ–і–∞ –і–≤–∞ –њ—А–µ–љ–Њ—Б–∞ —Ш–µ –љ–∞ —Г—И–µ—Б—В–∞–ї–Њ—Б—В–Є ќљ=1/p, –±–µ–Ј –Њ–±–Ј–Є—А–∞ –љ–∞ –§–Ю–Я –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞, –Ї–∞–Њ —И—В–Њ –≥—А–∞—Д –Ј–∞ p=3 –Є p=4 –њ–Њ–Ї–∞–Ј—Г—Ш—Г. –Ф–∞–Ї–ї–µ, –Њ—З—Г–≤–∞—Ъ–µ —А–∞–Ј–і–≤–Њ—Ш–љ–µ –Љ–Њ—Ы–Є –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ –Ј–∞—Е—В–µ–≤–∞ p=1, –Є–ї–Є –Љ–∞—Ъ–Є.
–Э–Є–≤–Њ –∞–±–µ—А–∞—Ж–Є—Ш–∞ –Ї–Њ—Ш–Є –±–Є –Ј–љ–∞—З–∞—Ш–љ–Њ —Б–љ–Є–ґ–∞–≤–∞–Њ –њ—А–µ–љ–Њ—Б –Ї–Њ–љ—В—А–∞—Б—В–∞ –Њ–њ—В–Є—З–Ї–Њ–≥ —Б–Ї–ї–Њ–њ–∞ –±–Є —В–∞–Ї–Њ—Т–µ –Ј–љ–∞—В–љ–Њ —Г–±–ї–∞–ґ–Є–Њ –Ј–∞—Е—В–µ–≤ –Ј–∞ –Љ–∞–ї–Є–Љ –њ–Є–Ї—Б–µ–ї–Њ–Љ. –£ —Б–ї—Г—З–∞—Ш—Г —В–µ–ї–µ—Б–Ї–Њ–њ–∞ –љ–∞ –Ч–µ–Љ—Щ–Є, –њ—А–µ —Б–≤–Є—Е, —В—Г —Ш–µ –љ–µ–Є–Ј–±–µ–ґ–љ–∞ –∞—В–Љ–Њ—Б—Д–µ—А—Б–Ї–∞ –≥—А–µ—И–Ї–∞ —В–∞–ї–∞—Б–љ–Њ–≥ —Д—А–Њ–љ—В–∞, –Ї–Њ—Ш–∞ —З–µ—Б—В–Њ –і–Њ–Ј–≤–Њ—Щ–∞–≤–∞ –≤–µ–ї–Є—З–Є–љ–µ –њ–Є–Ї—Б–µ–ї–∞ –Є –і–Њ –љ–µ–Ї–Њ–ї–Ї–Њ –њ—Г—В–∞ –≤–µ—Ы–µ –Њ–і –Э–∞–Є–Ї—Г–Є—Б—В–Њ–≤–µ –≥—А–∞–љ–Є—Ж–µ –Ј–∞ —Б–∞–≤—А—И–µ–љ –Њ–њ—В–Є—З–Ї–Є –Њ—В–≤–Њ—А. –£ –њ—А–∞–Ї—В–Є—З–љ–Є–Љ —Г—Б–ї–Њ–≤–Є–Љ–∞, –≥–Њ—А—Ъ–∞ –≥—А–∞–љ–Є—Ж–∞ –≤–µ–ї–Є—З–Є–љ–µ –њ–Є–Ї—Б–µ–ї–∞ —Ш–µ –≤–µ—Ы–∞ –Ј–∞ —А–∞—Ж–Є–Њ –∞—В–Љ–Њ—Б—Д–µ—А—Б–Ї–Њ–≥ FWHM –Є ќїF.
–§–Ю–Я –Є —Д—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –Ї–Њ–љ—В—А–∞—Б—В–∞
–§—Г–љ–Ї—Ж–Є—Ш–∞ –њ—А–µ–љ–Њ—Б–∞ –Ї–Њ–љ—В—А–∞—Б—В–∞ (—Б–Ї—А. –§–Я–Ъ, –µ–љ–≥. Contrast transfer function, CTF) —Ш–µ —Б–ї–Є—З–љ–∞ –§–Ю–Я, –њ–Њ—И—В–Њ —Б–µ –Ї–Њ—А–Є—Б—В–Є –і–Њ–Љ–µ–љ–Њ–Љ —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –і–∞ –±–Є –Є–Ј—А–∞–Ј–Є–ї–∞ —Б–≤–Њ—Ш—Б—В–≤–∞ –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ. –У–ї–∞–≤–љ–∞ —А–∞–Ј–ї–Є–Ї–∞ —Ш–µ —Г —В–Њ–Љ–µ —И—В–Њ –§–Я–Ъ –Ї–∞–Њ –Њ–±—Ш–µ–Ї—В –Є–Љ–∞ –љ–µ —Б–Є–љ—Г—Б–Њ–Є–і, –љ–µ–≥–Њ —В–Ј–≤. –Ї–≤–∞–і—А–∞—В–љ–Є —В–∞–ї–∞—Б, –Ї–Њ—Ш–Є –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –±–µ—Б–Ї—А–∞—Ш–∞–љ –љ–Є–Ј –љ–∞–Є–Ј–Љ–µ–љ–Є—З–љ–Є—Е –њ–∞—А–∞–ї–µ–ї–љ–Є—Е —Б–≤–µ—В–ї–Є—Е –Є —В–∞–Љ–љ–Є—Е –ї–Є–љ–Є—Ш–∞ –±–µ–Ј –њ–Њ—Б—В–µ–њ–µ–љ–Њ–≥ –њ—А–µ–ї–∞–Ј–∞ —Ш–µ–і–љ–Є—Е —Г –і—А—Г–≥–µ, —В—Ш. —Б–∞ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Є–Љ –≤–Є—Б–Њ–Ї–Є–Љ (—Б–≤–µ—В–ї–Є–Љ) –Є –љ–Є—Б–Ї–Є–Љ –љ–Є–≤–Њ–Њ–Љ –Ј—А–∞—З–µ—Ъ–∞.
 –°–Ы–Ш–Ъ–Р 12: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –Ш –§–£–Э–Ъ–¶–Ш–И–Р –Я–†–Х–Э–Ю–°–Р –Ъ–Ю–Э–Ґ–†–Р–°–Ґ–Р
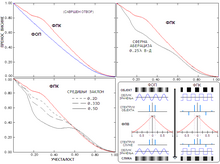
–°–Ы–Ш–Ъ–Р 12: –§–£–Э–Ъ–¶–Ш–И–Р –Ю–Я–Ґ–Ш–І–Ъ–Ю–У –Я–†–Х–Э–Ю–°–Р –Ш –§–£–Э–Ъ–¶–Ш–И–Р –Я–†–Х–Э–Ю–°–Р –Ъ–Ю–Э–Ґ–†–Р–°–Ґ–Р –°–ї–Є–Ї–∞ –і–µ—Б–љ–Њ –њ—А–Є–Ї–∞–Ј—Г—Ш–µ –≥—А–∞—Д –§–Я–Ъ –Є –§–Ю–Я –Ј–∞ —Б–∞–≤—А—И–µ–љ–Є –Њ—В–≤–Њ—А (–≥–Њ—А–µ –ї–µ–≤–Њ), –Ї–∞–Њ –Є –Ј–∞ –§–Я–Ъ —Г –њ—А–Є—Б—Г—Б—В–≤—Г —Б—Д–µ—А–љ–µ –∞–±–µ—А–∞—Ж–Є—Ш–µ (–≥–Њ—А–µ –і–µ—Б–љ–Њ) –Є —Б—А–µ–і–Є—И—Ъ–µ–≥ –Ј–∞–Ї–ї–Њ–љ–∞ (–і–Њ–ї–µ –ї–µ–≤–Њ). –£ —Б–ї—Г—З–∞—Ш—Г —Б–∞–≤—А—И–µ–љ–Њ–≥ –Њ–њ—В–Є—З–Ї–Њ–≥ –Њ—В–≤–Њ—А–∞, –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ —Б–Є–≥–љ–∞–ї–∞ –§–Я–Ъ —Ш–µ –±–Њ—Щ–Є —Г —Ж–µ–ї–Њ–Љ —А–∞—Б–њ–Њ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є. –Ю–≤–Њ —Ш–µ –њ–Њ—Б–ї–µ–і–Є—Ж–∞ —В–Њ–≥–∞ —И—В–Њ —Б–њ–µ–Ї—В—А—Г–Љ –Ї–≤–∞–і—А–∞—В–љ–Њ–≥ —В–∞–ї–∞—Б–∞, –Ј–∞ —А–∞–Ј–ї–Є–Ї—Г –Њ–і —Б–Є–љ—Г—Б–Њ–Є–і–∞ –Ї–Њ—Ш–Є —Ш–µ –Њ–њ–Є—Б–∞–љ —Б–∞–Љ–Њ —Б–∞ —Ш–µ–і–љ–Њ–Љ —Г—З–µ—Б—В–∞–ї–Њ—И—Ы—Г –Є –∞–Љ–њ–ї–Є—В—Г–і–Њ–Љ, –Ј–∞ –Њ–њ–Є—Б —Г –і–Њ–Љ–µ–љ—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є –Ј–∞—Е—В–µ–≤–∞ –±–µ—Б–Ї—А–∞—Ш–∞–љ –љ–Є–Ј —Г—З–µ—Б—В–∞–ї–Њ—Б—В–Є —Б–∞ –Њ–њ–∞–і–∞—Ш—Г—Ы–Њ–Љ –∞–Љ–њ–ї–Є—В—Г–і–Њ–Љ (–і–Њ–ї–µ –і–µ—Б–љ–Њ). –°–≤–∞–Ї–∞ –Њ–і –Њ–≤–Є—Е –∞–Љ–њ–ї–Є—В—Г–і–∞ —Б–µ –Љ–љ–Њ–ґ–Є —Б–∞ —Д—Г–љ–Ї—Ж–Є—Ш–Њ–Љ –њ—А–µ–љ–Њ—Б–∞ –≤–Є—Б–Є–љ–µ –§–Ю–Я-–∞ –Ј–∞ —Б–≤–∞–Ї—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В, –Є —Ъ–Є—Е–Њ–≤ –Ј–±–Є—А –њ—А–µ–і—Б—В–∞–≤—Щ–∞ –њ—А–µ–љ–Њ—Б –≤–Є—Б–Є–љ–µ –∞–Љ–њ–ї–Є—В—Г–і–µ –§–Я–Ъ-–∞ –Ј–∞ —В—Г —Г—З–µ—Б—В–∞–ї–Њ—Б—В.
–Ш –њ–Њ—А–µ–і —А–∞–Ј–ї–Є–Ї–µ —Г –Њ—Б–Њ–±–Є–љ–∞–Љ–∞ –Њ–±—Ш–µ–Ї—В–∞, –љ–µ–Љ–∞ –±–Є—В–љ–µ —А–∞–Ј–ї–Є–Ї–µ –Є–Ј–Љ–µ—Т—Г –§–Я–Ъ –Є –§–Ю–Я —Г –њ–Њ–≥–ї–µ–і—Г –і–µ—Ш—Б—В–≤–∞ –∞–±–µ—А–∞—Ж–Є—Ш–∞ –Є –Ј–∞–Ї–ї–Њ–љ–∞ –љ–∞ –Ї–∞–Ї–≤–Њ—Ы—Г –Њ–њ—В–Є—З–Ї–µ —Б–ї–Є–Ї–µ: —А–µ–ї–∞—В–Є–≤–љ–∞ –њ—А–Њ–Љ–µ–љ–∞ –Њ—И—В—А–Є–љ–µ —Б–ї–Є–Ї–µ —Ш–µ –≤—А–ї–Њ —Б–ї–Є—З–љ–∞ —Г –Њ–±–∞ —Б–ї—Г—З–∞—Ш–∞.
–Т–Є–і–Є —Ш–Њ—И
–†–µ—Д–µ—А–µ–љ—Ж–µ
–Ш–Ј–≤–Њ—А–Є
- Optical imaging and aberrations, V.N. Mahajan 1998
- Telescope optics, H. Rutten and M. van Venrooij, 1988
- Astronomical optics, D.J. Schroeder 1987
- Handbook of optical design, D. Malacara and Z. Malacara, 2004
- Handbook of optics, M. Bass (Optical Society of America), 1995
- Optical programs: SYNAPSIS, OSLO, Aberrator