![]() –ė–Ľ—É—Ā—ā—Ä–į—Ü–ł—ė–į –ł–∑—Ä–į–∑–į –∑–į —ė–Ķ–ī–į–Ĺ –ĺ–ī —ā–ł–Ņ–ł—á–Ĺ–ł—Ö –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į, –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—É –ļ–ĺ–Ķ—Ą–ł—Ü–ł—ė–Ķ–Ĺ—ā–į –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į —Ā –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ĺ–ľ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–≥ —É–≥–Ľ–į, –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ.
–ė–Ľ—É—Ā—ā—Ä–į—Ü–ł—ė–į –ł–∑—Ä–į–∑–į –∑–į —ė–Ķ–ī–į–Ĺ –ĺ–ī —ā–ł–Ņ–ł—á–Ĺ–ł—Ö –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į, –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—É –ļ–ĺ–Ķ—Ą–ł—Ü–ł—ė–Ķ–Ĺ—ā–į –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į —Ā –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ĺ–ľ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–≥ —É–≥–Ľ–į, –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ.
 –ė–Ľ—É—Ā—ā—Ä–į—Ü–ł—ė–į –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ĺ–≥ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ĺ–≥ —Ā–ł—Ā—ā–Ķ–ľ–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ł –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į –Ľ–Ķ—ā–į.
–ė–Ľ—É—Ā—ā—Ä–į—Ü–ł—ė–į –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ĺ–≥ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ĺ–≥ —Ā–ł—Ā—ā–Ķ–ľ–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ł –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į –Ľ–Ķ—ā–į.
–Ē–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł, —Ā—É —É—ė–Ķ–ī–Ĺ–ĺ –ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł, –į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į—ė—É –ľ–Ķ—Ä—É (–≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā) –Ņ–ĺ—ė–Ķ–ī–ł–Ĺ–ł—Ö –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł—Ö —Ā–ł–Ľ–į –ł –ľ–ĺ–ľ–Ķ–Ĺ–į—ā–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –Ņ–ĺ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł —ö–Ķ–Ĺ–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į –Ľ–Ķ—ā–į (–ļ–į–ĺ —ą—ā–ĺ —Ā—É –Ī—Ä–∑–ł–Ĺ–į, –≤–ł—Ā–ł–Ĺ–į, –Ĺ–į–Ņ–į–ī–Ĺ–ł —É–≥–į–ĺ, —É–≥–į–ĺ –ļ–Ľ–ł–∑–į—ö–į, –ĺ—ā–ļ–Ľ–ĺ–Ĺ –ļ–ĺ–ľ–į–Ĺ–ī–Ĺ–ł—Ö –Ņ–ĺ–≤—Ä—ą–ł–Ĺ–į –ł—ā–ī). –ó–į –ī–Ķ—Ą–ł–Ĺ–ł—Ā–į–Ĺ–ĺ —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ĺ–ĺ —Ā—ā–į—ö–Ķ, –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ –ł –ĺ—Ā—Ü–ł–Ľ–ĺ–≤–į—ö–Ķ –≤—Ä–Ķ–ī–Ĺ–ĺ—Ā—ā–ł –ĺ–≤–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į, –Ņ–ĺ—Ā–Ľ–Ķ —Ā–≤–į–ļ–ĺ–≥ –Ņ–ĺ—Ä–Ķ–ľ–Ķ—õ–į—ė–į. –ą–Ķ–ī–Ĺ–į—á–ł–Ĺ–Ķ –ļ—Ä–Ķ—ā–į—ö–į —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–Ķ –∑–į –į–Ĺ–į–Ľ–ł–∑—É –ĺ–≤–ł—Ö –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–į –ł –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į, –Ĺ–į–ļ–ĺ–Ĺ –Ņ–ĺ—Ä–Ķ–ľ–Ķ—õ–į—ė–į. –Ē–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–Ķ –∑–į –Ľ–ł–Ĺ–Ķ–į—Ä–ł–∑–į—Ü–ł—ė—É (–Ņ–ĺ—ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤—ô–Ķ—ö–Ķ) –ĺ–≤–ł—Ö —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –ļ—Ä–Ķ—ā–į—ö–į, —ā–į–ļ–ĺ –ī–į —Ā–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–į –ľ–ĺ–≥—É —ė–Ķ–ī–Ĺ–ĺ—Ā—ā–į–≤–Ĺ–ł—ė–Ķ –į–Ĺ–į–Ľ–ł–∑–ł—Ä–į—ā–ł.
–Ē–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł –ī–Ķ—Ą–ł–Ĺ–ł—ą—É –ł —É—Ā–Ľ–ĺ–≤—ô–į–≤–į—ė—É –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ –ĺ–Ī–Ľ–ł–ļ–į –ļ—Ä–Ķ—ā–į—ö–į –ĺ–ļ–ĺ —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ĺ–ĺ–≥ —Ā—ā–į—ö–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ. –°–ļ—É–Ņ —Ā–≤–ł—Ö –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł (–∑–į—ė–Ķ–ī–Ĺ–ĺ —Ā–į –ī—Ä—É–≥–ł–ľ –ļ–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į–ľ–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ), –Ņ–ĺ–≤–Ķ–∑–į–Ĺ–ĺ —É —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į–ľ–į –ļ—Ä–Ķ—ā–į—ö–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –ľ–ĺ–ī–Ķ–Ľ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ. –ě–≤–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –ľ–ĺ–ī–Ķ–Ľ–ł —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–Ķ —É —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä–ł–ľ–į –Ľ–Ķ—ā–į –∑–į –ł–Ĺ–∂–Ķ—ö–Ķ—Ä—Ā–ļ—É –į–Ĺ–į–Ľ–ł–∑—É —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ, –į —É —Ä–Ķ–į–Ľ–Ĺ–ĺ–ľ –≤—Ä–Ķ–ľ–Ķ–Ĺ—É, —Ā–Ľ—É–∂–Ķ –∑–į –ĺ–Ī—É–ļ—É –ł —ā—Ä–Ķ–Ĺ–į–∂—É –Ņ–ł–Ľ–ĺ—ā–į.
–£ –ł–Ĺ–∂–Ķ—ö–Ķ—Ä—Ā–ļ–ĺ—ė –Ņ—Ä–į–ļ—Ā–ł, –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł —Ā–Ķ –ī–Ķ–Ľ–Ķ —É —ā—Ä–ł –≥—Ä—É–Ņ–į—Ü–ł—ė–Ķ:
- –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł –Ņ–ĺ–Ľ–ĺ–∂–į—ė–į (—Ā—ā–į—ā–ł—á–ļ–ł, –Ņ–ĺ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–ľ —É–≥–Ľ—É őĪ –ł —É–≥–Ľ—É –ļ–Ľ–ł–∑–į—ö–į ő≤),
- –Ņ—Ä–ł–≥—É—ą–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł (–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł, –Ņ–ĺ —É–≥–į–ĺ–Ĺ–ĺ—ė –Ī—Ä–∑–ł–Ĺ–ł, –ĺ–ļ–ĺ –ĺ—Ā–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ q, r –ł p) –ł
- —É–Ĺ–į–ļ—Ä—Ā–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł (‚Äě–ļ—É–Ņ–Ľ–ĺ–≤–į–Ĺ–ł‚Äú, —É—ā–ł—Ü–į—ė –ļ–Ľ–ł–∑–į—ö–į –Ĺ–į –≤–į—ô–į—ö–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ł –ĺ–Ī—Ä–Ĺ—É—ā–ĺ).
–§–ł–∑–ł–ļ–į–Ľ–Ĺ–ĺ—Ā—ā
 –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ –Ľ–Ķ—ā–į (–Ī—Ä–∑–ł–Ĺ—Ā–ļ–ł).
–ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ –Ľ–Ķ—ā–į (–Ī—Ä–∑–ł–Ĺ—Ā–ļ–ł).
–ź–Ĺ–į–Ľ–ł—ā–ł—á–ļ–į –ī–Ķ—Ą–ł–Ĺ–ł—Ü–ł—ė–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł —Ā–Ķ –∑–į—Ā–Ĺ–ł–≤–į –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ—É –Ľ–ł–Ĺ–Ķ–į—Ä–Ĺ–ł—Ö —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į, –ļ–ĺ—ė–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į—ė—É —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ĺ–ĺ —Ā—ā–į—ö–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ. –£ —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į–ľ–į —Ā–Ķ –Ņ—Ä–ł–ļ–į–∑—É—ė—É —Ā–ł–Ľ–Ķ –ł –ľ–ĺ–ľ–Ķ–Ĺ—ā–ł —É –ĺ–Ī–Ľ–ł–ļ—É –∑–Ī–ł—Ä–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–į —ö–ł—Ö–ĺ–≤–ł—Ö –≥—Ä–į–ī–ł—ė–Ķ–Ĺ–į—ā–į –Ņ–ĺ –ĺ–ī—Ä–Ķ—í–Ķ–Ĺ–ĺ–ľ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—É –ł –Ņ—Ä–ł—Ä–į—ą—ā–į—ė–į —ā–ĺ–≥–į –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į. –ě–≤–ł –≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā–ł —É –Ī–Ķ–∑–ī–ł–ľ–Ķ–Ĺ–∑–ł–ĺ–Ĺ–ĺ–ľ –ĺ–Ī–Ľ–ł–ļ—É –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į—ė—É –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł. –ü–ĺ—ą—ā–ĺ —ė–Ķ –į–≤–ł–ĺ–Ĺ —Ā–ł–ľ–Ķ—ā—Ä–ł—á–į–Ĺ, —É –ĺ–ī–Ĺ–ĺ—Ā—É –Ĺ–į –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–Ĺ—É —Ä–į–≤–į–Ĺ, —É –ļ–ĺ—ė–ĺ—ė —Ā–Ķ –Ĺ–į–Ľ–į–∑–ł –ł —É–∑–ī—É–∂–Ĺ–į –ĺ—Ā–į, —Ā–į—Ā–≤–ł–ľ —Ā–Ķ –ĺ–ī–≤–ĺ—ė–Ķ–Ĺ–ĺ –į–Ĺ–į–Ľ–ł–∑–ł—Ä–į—ė—É —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–Ķ —É–∑–ī—É–∂–Ĺ–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ĺ–ī –Ņ–ĺ–Ņ—Ä–Ķ—á–Ĺ–ĺ-—Ā–ľ–Ķ—Ä–Ĺ–Ķ.
–°—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ —Ā—É –Ĺ–Ķ–ĺ–ī–≤–ĺ—ė–ł–≤–ł –Ņ–ĺ—ė–ľ–ĺ–≤–ł, —ā–Ķ –ł —Ā–≤–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł –ł–ľ–į—ė—É —É—ā–ł—Ü–į—ė –Ĺ–į —ā–Ķ –ĺ–Ī–Ķ –ĺ–Ī–Ľ–į—Ā—ā–ł –Ņ–ĺ–≤–Ķ–∑–į–Ĺ–Ķ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į—ā–ł–ļ–Ķ. –ú–Ĺ–ĺ–≥–ł, —Ā–į –ľ–į—ö–ł–ľ —É—ā–ł—Ü–į—ė–Ķ–ľ —Ā–Ķ –∑–į–Ĺ–Ķ–ľ–į—Ä—É—ė—É, –į –ī–ĺ–ľ–ł–Ĺ–į–Ĺ—ā–Ĺ–ł—ė–ł —Ā–Ķ —É–ļ—ô—É—á—É—ė—É —É —Ä–į–∑–ľ–į—ā—Ä–į—ö–Ķ.[1][2][3]
–£ —É–∑–ī—É–∂–Ĺ–ĺ–ľ –ļ—Ä–Ķ—ā–į—ö—É
–£–∑–ī—É–∂–Ĺ–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā –Ņ—Ä–ĺ–ł–∑–ł–Ľ–į–∑–ł –ł–∑ —É—Ā–Ľ–ĺ–≤–į —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ķ –ī—É–∂ –ĺ—Ā–į ‚ÄěX‚Äú –ł ‚ÄěZ‚Äú –ł –ĺ–ļ–ĺ ‚ÄěY‚Äú, –ł–∑ –Ņ—Ä–į–ļ—ā–ł—á–Ĺ–ł—Ö —Ä–į–∑–Ľ–ĺ–≥–į, —Ä–į–∑–ľ–į—ā—Ä–į–Ĺ–ĺ —É –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ĺ–ľ —Ā–ł—Ā—ā–Ķ–ľ—É –Ľ–Ķ—ā–į (–Ī—Ä–∑–ł–Ĺ—Ā–ļ–ĺ–ľ). –£ —ā–ĺ–ľ–Ķ –Ņ–ĺ–ļ—Ä–Ķ—ā–Ĺ–ĺ–ľ —Ā–ł—Ā—ā–Ķ–ľ—É, –Ņ–ĺ–ļ–Ľ–į–Ņ–į —Ā–Ķ ‚ÄěX‚Äú –ĺ—Ā–į –ł –Ņ—Ä–į–≤–į—Ü –ļ—Ä–Ķ—ā–į—ö–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ. –ú–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –Ņ—Ä–ł–ļ–į–∑ —ā–ł—Ö —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ĺ–ł—Ö —Ā—ā–į—ö–į —Ā—É –Ľ–ł–Ĺ–Ķ—Ä–Ĺ–Ķ —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–Ķ, –ļ–ĺ—ė–Ķ —Ā–į–ī—Ä–∂–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł, –ļ–į–ĺ –≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā–Ķ –Ņ–ĺ –ĺ–ī—Ä–Ķ—í–Ķ–Ĺ–ĺ–ľ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—É –Ľ–Ķ—ā–į. –ą–Ķ–ī–Ĺ–į—á–ł–Ĺ–Ķ —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ķ:

–ü–ĺ—Ā–Ľ–Ķ –Ī–Ķ–∑–ī–ł–ľ–Ķ–Ĺ–ł—Ā–į—ö–į —Ā–≤–ł—Ö –ī–Ķ–Ľ–ĺ–≤–į —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –ł —ö–ł—Ö–ĺ–≤–ł—Ö —Ā—Ä–Ķ—í–ł–≤–į—ö–į, —É —ö–ł—Ö–ĺ–≤–ł–ľ —Ā–į–Ī–ł—Ä—Ü–ł–ľ–į —Ā–Ķ –Ņ–ĺ—ė–į–≤—ô—É—ė—É –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł (—É –Ī–Ķ–∑–ī–ł–ľ–Ķ–Ĺ–∑–ł–ĺ–Ĺ–ĺ–ľ –ĺ–Ī–Ľ–ł–ļ—É).
 ‚Äď –Ņ—Ä–ł—Ä–į—Ā—ā —É–∑–≥–ĺ–Ĺ–į –Ņ–ĺ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–ľ —É–≥–Ľ—É (–≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā —É–∑–≥–ĺ–Ĺ–į)
‚Äď –Ņ—Ä–ł—Ä–į—Ā—ā —É–∑–≥–ĺ–Ĺ–į –Ņ–ĺ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–ľ —É–≥–Ľ—É (–≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā —É–∑–≥–ĺ–Ĺ–į) ‚Äď –Ņ—Ä–ł—Ä–į—Ā—ā –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į –Ņ–ĺ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–ľ —É–≥–Ľ—É, –ľ–Ķ—Ä–į —Ā—ā–į—ā–ł—á–ļ–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł (—Ā–≤–ĺ–ī–ł —Ā–Ķ –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī —Ä–Ķ–∑–Ķ—Ä–≤–Ķ —Ā—ā–į—ā–ł—á–ļ–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł –≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā–į —É–∑–≥–ĺ–Ĺ–į)
‚Äď –Ņ—Ä–ł—Ä–į—Ā—ā –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į –Ņ–ĺ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–ľ —É–≥–Ľ—É, –ľ–Ķ—Ä–į —Ā—ā–į—ā–ł—á–ļ–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł (—Ā–≤–ĺ–ī–ł —Ā–Ķ –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī —Ä–Ķ–∑–Ķ—Ä–≤–Ķ —Ā—ā–į—ā–ł—á–ļ–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł –≥—Ä–į–ī–ł—ė–Ķ–Ĺ—ā–į —É–∑–≥–ĺ–Ĺ–į) ‚Äď –Ņ—Ä–ł–≥—É—ą–Ķ—ö–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–Ķ—ö–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī –Ī—Ä–∑–ł–Ĺ–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–≥ —É–≥–Ľ–į, –≥–ī–Ķ —ė–Ķ –ł –≤—Ä–Ķ–ľ–Ķ –ĺ–Ī–Ķ–∑–ī–ł–ľ–Ķ–Ĺ–∑–ł–ĺ–Ĺ–ł—Ā–į–Ĺ–ĺ —Ā —Ą–į–ļ—ā–ĺ—Ä–ĺ–ľ
‚Äď –Ņ—Ä–ł–≥—É—ą–Ķ—ö–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–Ķ—ö–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī –Ī—Ä–∑–ł–Ĺ–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–≥ —É–≥–Ľ–į, –≥–ī–Ķ —ė–Ķ –ł –≤—Ä–Ķ–ľ–Ķ –ĺ–Ī–Ķ–∑–ī–ł–ľ–Ķ–Ĺ–∑–ł–ĺ–Ĺ–ł—Ā–į–Ĺ–ĺ —Ā —Ą–į–ļ—ā–ĺ—Ä–ĺ–ľ 
 ‚Äď –Ņ—Ä–ł–≥—É—ą–Ķ—ö–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–Ķ—ö–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į
‚Äď –Ņ—Ä–ł–≥—É—ą–Ķ—ö–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–Ķ—ö–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į 
 ‚Äď –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā –ļ—Ä–ľ–ł–Ľ–į –≤–ł—Ā–ł–Ĺ–Ķ
‚Äď –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā –ļ—Ä–ľ–ł–Ľ–į –≤–ł—Ā–ł–Ĺ–Ķ ‚Äď –Ņ—Ä–ł–≥—É—ą–Ķ—ö–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–Ķ—ö–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ –ĺ—ā–ļ–Ľ–ĺ–Ĺ–į –ļ—Ä–ľ–ł–Ľ–į —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–ĺ–≥ —Ä–Ķ–Ņ–į[1][4][5][6]
‚Äď –Ņ—Ä–ł–≥—É—ą–Ķ—ö–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ–ł—ö–Ķ—ö–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ –ĺ—ā–ļ–Ľ–ĺ–Ĺ–į –ļ—Ä–ľ–ł–Ľ–į —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–ĺ–≥ —Ä–Ķ–Ņ–į[1][4][5][6]
–£ –Ņ–ĺ–Ņ—Ä–Ķ—á–Ĺ–ĺ-—Ā–ľ–Ķ—Ä–Ĺ–ĺ–ľ –ļ—Ä–Ķ—ā–į—ö—É
–õ–ł–Ĺ–Ķ—Ä–Ĺ–Ķ —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–Ķ —Ä–į–≤–Ĺ–ĺ—ā–Ķ–∂–Ķ, —É –Ņ–ĺ–Ņ—Ä–Ķ—á–Ĺ–ĺ-—Ā–ľ–Ķ—Ä–Ĺ–ĺ–ľ –ļ—Ä–Ķ—ā–į—ö—É —Ā—É:

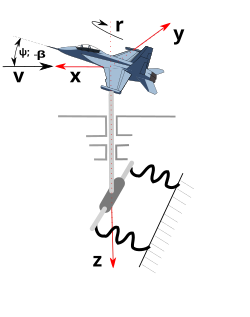 –í–Ķ—ā—Ä–Ķ–Ĺ–ł—Ü–į, —ą–Ķ–ľ–į—ā—Ā–ļ–ł –Ņ—Ä–ł–ļ–į–∑ —É—Ä–Ķ—í–į—ė–į –∑–į –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ –Ņ—Ä–į–≤—Ü—É, –ľ–Ķ—ā–ĺ–ī–ĺ–ľ —Ā–Ľ–ĺ–Ī–ĺ–ī–Ĺ–ł—Ö –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į. –Ē–ł–Ĺ–į–ľ–ł—á–ļ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ, –ĺ—Ā–Ķ –Ľ–Ķ—ā–į.
–í–Ķ—ā—Ä–Ķ–Ĺ–ł—Ü–į, —ą–Ķ–ľ–į—ā—Ā–ļ–ł –Ņ—Ä–ł–ļ–į–∑ —É—Ä–Ķ—í–į—ė–į –∑–į –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ –Ņ—Ä–į–≤—Ü—É, –ľ–Ķ—ā–ĺ–ī–ĺ–ľ —Ā–Ľ–ĺ–Ī–ĺ–ī–Ĺ–ł—Ö –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į. –Ē–ł–Ĺ–į–ľ–ł—á–ļ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ, –ĺ—Ā–Ķ –Ľ–Ķ—ā–į.–£ —ö–ł—Ö–ĺ–≤–ł–ľ —Ā–į–Ī–ł—Ä—Ü–ł–ľ–į —Ā–Ķ –Ņ–ĺ—ė–į–≤—ô—É—ė—É –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł (—É –Ī–Ķ–∑–ī–ł–ľ–Ķ–Ĺ–∑–ł–ĺ–Ĺ–ĺ–ľ –ĺ–Ī–Ľ–ł–ļ—É).
 ‚Äď –Ņ—Ä–ł—Ä–į—Ā—ā –Ī–ĺ—á–Ĺ–Ķ —Ā–ł–Ľ–Ķ, —É—Ā–Ľ–Ķ–ī –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ —É–≥–Ľ–į –ļ–Ľ–ł–∑–į—ö–į
‚Äď –Ņ—Ä–ł—Ä–į—Ā—ā –Ī–ĺ—á–Ĺ–Ķ —Ā–ł–Ľ–Ķ, —É—Ā–Ľ–Ķ–ī –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ —É–≥–Ľ–į –ļ–Ľ–ł–∑–į—ö–į ‚Äď –Ņ—Ä–ł–≥—É—ą–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤ —É –≤–į—ô–į—ö—É, –Ņ–ĺ —É–≥–į–ĺ–Ĺ–ĺ—ė –Ī—Ä–∑–ł–Ĺ–ł –≤–į—ô–į—ö–į p
‚Äď –Ņ—Ä–ł–≥—É—ą–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤ —É –≤–į—ô–į—ö—É, –Ņ–ĺ —É–≥–į–ĺ–Ĺ–ĺ—ė –Ī—Ä–∑–ł–Ĺ–ł –≤–į—ô–į—ö–į p ‚Äď —É–Ĺ–į–ļ—Ä—Ā–Ĺ–ł (—Ā–Ņ—Ä–Ķ–≥–Ĺ—É—ā–ł) –ī–Ķ—Ä–ł–≤–į—ā–ł–≤, –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤–į—ô–į—ö–į —É—Ā–Ľ–Ķ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ —Ā–ļ—Ä–Ķ—ā–į—ö–į r
‚Äď —É–Ĺ–į–ļ—Ä—Ā–Ĺ–ł (—Ā–Ņ—Ä–Ķ–≥–Ĺ—É—ā–ł) –ī–Ķ—Ä–ł–≤–į—ā–ł–≤, –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤–į—ô–į—ö–į —É—Ā–Ľ–Ķ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ —Ā–ļ—Ä–Ķ—ā–į—ö–į r ‚Äď —É–Ĺ–į–ļ—Ä—Ā–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤, –ľ–ĺ–ľ–Ķ–Ĺ—ā —Ā–ļ—Ä–Ķ—ā–į—ö–į —É—Ā–Ľ–Ķ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ –≤–į—ô–į—ö–į p
‚Äď —É–Ĺ–į–ļ—Ä—Ā–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤, –ľ–ĺ–ľ–Ķ–Ĺ—ā —Ā–ļ—Ä–Ķ—ā–į—ö–į —É—Ā–Ľ–Ķ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ –≤–į—ô–į—ö–į p ‚Äď –Ņ—Ä–ł–≥—É—ą–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤, –ľ–ĺ–ľ–Ķ–Ĺ—ā —Ā–ļ—Ä–Ķ—ā–į—ö–į —É—Ā–Ľ–Ķ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ —Ā–ļ—Ä–Ķ—ā–į—ö–į r
‚Äď –Ņ—Ä–ł–≥—É—ą–Ĺ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤, –ľ–ĺ–ľ–Ķ–Ĺ—ā —Ā–ļ—Ä–Ķ—ā–į—ö–į —É—Ā–Ľ–Ķ–ī —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ —Ā–ļ—Ä–Ķ—ā–į—ö–į r ‚Äď –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā –ļ—Ä–ł–Ľ–į—Ü–į
‚Äď –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā –ļ—Ä–ł–Ľ–į—Ü–į ‚Äď –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā –ļ—Ä–ľ–ł–Ľ–į –Ņ—Ä–į–≤—Ü–į[1][7][8][9]
‚Äď –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā –ļ—Ä–ľ–ł–Ľ–į –Ņ—Ä–į–≤—Ü–į[1][7][8][9]
–ú–Ķ—ā–ĺ–ī–Ķ –ĺ–ī—Ä–Ķ—í–ł–≤–į—ö–į –≤—Ä–Ķ–ī–Ĺ–ĺ—Ā—ā–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į
–ź–Ĺ–į–Ľ–ł—ā–ł—á–ļ–į
–£ –Ņ–ĺ—á–Ķ—ā–Ĺ–ĺ—ė —Ą–į–∑–ł –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į—ö–į, –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł —Ā–Ķ –ĺ–ī—Ä–Ķ—í—É—ė—É –į–Ĺ–į–Ľ–ł—ā–ł—á–ļ–ł. –Ę–ĺ —ė–Ķ –Ņ—Ä–į–ļ—ā–ł—á–Ĺ–ĺ –Ņ—Ä–≤–ĺ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–≤–į—ö–Ķ —É –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į—ö—É, –ļ–į–ī–į —Ā–Ķ –Ņ—Ä–Ķ–ľ–į –ī–ĺ–Ņ—Ä–ł–Ĺ–ĺ—Ā–ł–ľ–į –Ņ–ĺ—ė–Ķ–ī–ł–Ĺ–ł—Ö –ī–Ķ–Ľ–ĺ–≤–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ĺ–ī—Ä–Ķ—í—É—ė—É —Ā–į–Ī–ł—Ä—Ü–ł –ĺ–ī–Ķ—í–Ķ–Ĺ–ĺ–≥ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į. –Ę–ł –ī–ĺ–Ņ—Ä–ł–Ĺ–ĺ—Ā–ł —Ā–Ķ –ĺ–ī—Ä–Ķ—í—É—ė—É –Ņ—Ä–ĺ—Ä–į—á—É–Ĺ—Ā–ļ–ł –ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤—É —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–Ķ –Ņ–ĺ–∑–Ĺ–į—ā–ł—Ö –≤—Ä–Ķ–ī–Ĺ–ĺ—Ā—ā–ł –∑–į –ī–ĺ—ā–ł—á–Ĺ–ł –ī–Ķ–ĺ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ.
 –®–Ķ–ľ–į—ā—Ā–ļ–ł –Ņ—Ä–ł–ļ–į–∑ —É—Ä–Ķ—í–į—ė–į –∑–į –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł, –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –ļ—Ä—É—ā–ł—Ö –Ņ—Ä–ł–Ĺ—É–ī–Ĺ–ł—Ö –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į.
–®–Ķ–ľ–į—ā—Ā–ļ–ł –Ņ—Ä–ł–ļ–į–∑ —É—Ä–Ķ—í–į—ė–į –∑–į –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł, –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –ļ—Ä—É—ā–ł—Ö –Ņ—Ä–ł–Ĺ—É–ī–Ĺ–ł—Ö –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į.
–£ —ā–ĺ–ľ –ĺ–Ī–Ľ–ł–ļ—É —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–Ķ –∑–į –Ņ—Ä–Ķ–Ľ–ł–ľ–ł–Ĺ–į—Ä–Ĺ–Ķ —Ą–į–∑–Ķ –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į—ö–į (–Ņ—Ä–≤–ĺ–ľ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–≤–į—ö—É), —É –Ņ—Ä–≤–ł–ľ —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–į–ľ–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ.[1]
–ē–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–į, —É –į–Ķ—Ä–ĺ—ā—É–Ĺ–Ķ–Ľ—É
 –£–Ĺ—É—ā—Ä–į—ą—ö–į –į–Ķ—Ä–ĺ–≤–į–≥–į, —Ā –ī–≤–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ–į —Ā–Ľ–ĺ–Ī–ĺ–ī–Ķ, –∑–į –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –ļ—Ä—É—ā–ł—Ö –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į.
–£–Ĺ—É—ā—Ä–į—ą—ö–į –į–Ķ—Ä–ĺ–≤–į–≥–į, —Ā –ī–≤–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ–į —Ā–Ľ–ĺ–Ī–ĺ–ī–Ķ, –∑–į –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —Ā –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –ļ—Ä—É—ā–ł—Ö –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į.
–£ –Ĺ–į—Ä–Ķ–ī–Ĺ–ĺ—ė —Ą–į–∑–ł –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ, –ļ–į–ī–į —ė–Ķ –Ņ–ĺ–∑–Ĺ–į—ā –Ņ—Ä–Ķ–Ľ–ł–ľ–ł–Ĺ–į—Ä–Ĺ–ł —ö–Ķ–Ĺ –ĺ–Ī–Ľ–ł–ļ –ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—ė–į, —ā–į–ī–į —Ā–Ķ –ł–∑—Ä–į—í—É—ė–Ķ —ö–Ķ–Ĺ —Ą–ł–∑–ł—á–ļ–ł –ľ–ĺ–ī–Ķ–Ľ —É —Ā–ľ–į—ö–Ķ–Ĺ–ĺ—ė —Ä–į–∑–ľ–Ķ—Ä–ł, –∑–į –ł—Ā–Ņ–ł—ā–ł–≤–į—ö–Ķ –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ —É –į–Ķ—Ä–ĺ—ā—É–Ĺ–Ķ–Ľ—É. –£ –ĺ–ļ–≤–ł—Ä—É —ā–ł—Ö –ł—Ā–Ņ–ł—ā–ł–≤–į—ö–į —ė–Ķ –ł –ľ–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į.
–ú–Ķ—Ä–Ķ—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į —É –į–Ķ—Ä–ĺ—ā—É–Ĺ–Ķ–Ľ—É —Ā–Ķ –∑–į—Ā–Ĺ–ł–≤–į –Ĺ–į –ī–≤–į –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į:
- –ľ–Ķ—ā–ĺ–ī –Ņ–ĺ—Ä–Ķ–ľ–Ķ—õ–į—ė–į —Ā —ā–ł–Ņ–ł—á–Ĺ–ł–ľ –ļ—Ä–į—ā–ļ–ĺ—ā—Ä–į—ė–Ĺ–ł–ľ —É–Ľ–į–∑–ĺ–ľ, –ĺ–ī–≥–ĺ–≤–ĺ—Ä —Ā–Ľ–ĺ–Ī–ĺ–ī–Ĺ–Ķ –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–Ķ –ł
- –ľ–Ķ—ā–ĺ–ī –ī—É–≥–ĺ—ā—Ä–į—ė–Ĺ–Ķ –Ņ—Ä–ł–Ĺ—É–ī–Ķ, –ļ—Ä—É—ā–ł–ľ –ĺ—Ā—Ü–ł–Ľ–į—Ü–ł—ė–į–ľ–į
–ö–ĺ–ī –ĺ–Ī–į –ľ–Ķ–ī–ĺ–ī–į, —Ā–Ĺ–ł–ľ–į —Ā–Ķ –ĺ–ī–≥–ĺ–≤–ĺ—Ä –ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤—É —ö–Ķ–≥–ĺ–≤–Ķ –į–Ĺ–į–Ľ–ł–∑–Ķ, –ł–∑–ī–≤–į—ė–į—ė—É —Ā–Ķ –ĺ–ī–≥–ĺ–≤–į—Ä–į—ė—É—õ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł. –ó–į –ĺ–≤–į –ľ–Ķ—Ä–Ķ—ö–į —ė–Ķ –Ņ–ĺ—ā—Ä–Ķ–Ī–Ĺ–ĺ –ĺ–Ī–Ķ–∑–Ī–Ķ–ī–ł—ā–ł –ĺ–ī–≥–ĺ–≤–į—Ä–į—ė—É—õ–Ķ –ľ–Ķ—Ä–Ĺ–Ķ —É—Ä–Ķ—í–į—ė–Ķ –ł –ľ–Ķ—Ä–Ĺ—É –Ņ–ĺ—Ā—ā–į–≤—É. –Ě–Ķ–ļ–ł –ĺ–ī –ľ–Ķ—Ä–Ĺ–ł—Ö —É—Ä–Ķ—í–į—ė–į —Ā—É –ł–Ľ—É—Ā—ā—Ä–ĺ–≤–į–Ĺ–ł –Ĺ–į –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–ľ —Ā–Ľ–ł–ļ–į–ľ–į.
–ü–ĺ—Ā–Ľ–Ķ –ĺ–≤–Ķ –Ķ–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–Ķ —Ą–į–∑–Ķ –ĺ–ī—Ä–Ķ—í—É—ė—É —Ā–Ķ –≤—Ä–Ķ–ī–Ĺ–ĺ—Ā—ā–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į, –∑–į –Ĺ–ł–≤–ĺ –Ņ—Ä–ĺ—ā–ĺ—ā–ł–Ņ—Ā–ļ–ĺ–≥ —Ä–į–∑–≤–ĺ—ė–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ.[10][11][12]
–ē–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–į, —É –Ľ–Ķ—ā—É –ł —Ä–į–∑–≤–ĺ—ė–Ĺ–ĺ–ľ —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä—É
–°–Ľ–Ķ–ī–Ķ—õ–į —Ą–į–∑–į —ė–Ķ –ľ–Ķ—Ä–Ķ—ö–Ķ —É –Ľ–Ķ—ā—É, –Ņ—Ä–ł –ł—Ā–Ņ–ł—ā–ł–≤–į—ö—É –Ņ—Ä–ĺ—Ä–ĺ—ā–ł–Ņ–į. –°–į —É–≥—Ä–į—í–Ķ–Ĺ–ĺ–ľ —Ā–Ņ–Ķ—Ü–ł—ė–į–Ľ–Ĺ–ĺ–ľ –ĺ–Ņ—Ä–Ķ–ľ–ĺ–ľ –ł —Ä–į—Ā–Ņ–ĺ—Ä–Ķ–ī–ĺ–ľ —Ā–Ķ–Ĺ–∑–ĺ—Ä–į (–ī–į–≤–į—á–į), —Ā–Ĺ–ł–ľ–į —Ā–Ķ –ĺ–ī–≥–ĺ–≤–ĺ—Ä –į–≤–ł–ĺ–Ĺ–į —É –Ľ–Ķ—ā—É –Ĺ–į —É–≤–Ķ–ī–Ķ–Ĺ–ł —ā–ł–Ņ–ł—á–Ĺ–ł –Ņ–ĺ—Ä–Ķ–ľ–Ķ—õ–į—ė. –ú–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ĺ–ľ –į–Ĺ–į–Ľ–ł–∑–ĺ–ľ —ā–ĺ–≥–į –ĺ–ī–≥–ĺ–≤–ĺ—Ä–į –≤—Ä—ą–ł —Ā–Ķ –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł–ļ–į—Ü–ł—ė–į –į–Ķ—Ä–Ķ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į –į–≤–ł–ĺ–Ĺ–į, –ľ–Ķ—í—É –ļ–ĺ—ė–ł–ľ–į –ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į.
–ú–Ķ—ā–ĺ–ī–Ķ –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł–ļ–į—Ü–ł—ė–Ķ –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į —É –Ľ–Ķ—ā—É –∑–į—Ā–Ĺ–ł–≤–į—ė—É —Ā–Ķ –Ĺ–į –ī–ĺ–Ī—Ä–ĺ –Ņ–ĺ–∑–Ĺ–į—ā–ł–ľ —ā–Ķ–ĺ—Ä–ł—ė—Ā–ļ–ł–ľ –Ņ–ĺ—Ā—ā–į–≤–ļ–į–ľ–į. –Ē–ĺ–Ī–ł—ė–Ķ–Ĺ–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł –ľ–Ķ—í—É—Ā–ĺ–Ī–Ĺ–ĺ —Ā–Ķ —É—Ā–į–≥–Ľ–į—ą–į–≤–į—ė—É –Ĺ–į –Ĺ–ł–≤–ĺ—É –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–į –ł –ļ–ĺ—Ä–ł—Ā—ā–Ķ —Ā–Ķ –∑–į –į–∂—É—Ä–ł—Ä–į—ö–Ķ –Ī–į–∑–Ķ –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł—Ö –Ņ–ĺ–ī–į—ā–į–ļ–į –∑–į –ī–ĺ—ā–ł—á–Ĺ—É –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü—É, —É —Ā–≤–ł–ľ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł—ė–į–ľ–į. –°–ł—Ā—ā–Ķ–ľ –ī–ĺ—Ā—ā–ł–∂–Ķ –∑–į—Ö—ā–Ķ–≤–į–Ĺ–ł —Ā—ā–į–Ĺ–ī–į—Ä–ī –Ņ—É—ā–Ķ–ľ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–≥ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į—ö–į –ī–ł–Ĺ–į–ľ–ł–ļ–Ķ. –ú–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –ľ–ĺ–ī–Ķ–Ľ –ĺ–Ī—É—Ö–≤–į—ā–į –≤–Ķ–Ľ–ł–ļ–ł –Ī—Ä–ĺ—ė —Ā–Ņ–ĺ—ô–Ĺ–ł—Ö –ł —É–Ĺ—É—ā—Ä–į—ą—ö–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į –ļ–į–ĺ —ą—ā–ĺ —Ā—É —Ā—ā–į—ā–ł—á–ļ–ł –ł –ī–ł–Ĺ–į–ľ–ł—á–ļ–ł –Ņ—Ä–ł—ā–ł—Ā–į–ļ –ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –≤–į–∑–ī—É—Ö–į –ł —ö–ł—Ö–ĺ–≤ —É—ā–ł—Ü–į—ė –Ĺ–į –ĺ—Ā—ā–į–Ľ–Ķ –ļ–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–Ķ. –ó–į—ā–ł–ľ, –ĺ–Ī—É—Ö–≤–į—ā–į —Ā–≤–Ķ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł—ė–Ķ —ā–Ķ—Ä–Ķ—ā–į –ł —Ā–≤–Ķ –ĺ–Ī–Ľ–ł–ļ–Ķ –ł –Ī—Ä–∑–ł–Ĺ–Ķ –Ľ–Ķ—ā–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ. –ö–≤–į–Ľ–ł—ā–Ķ—ā–į–Ĺ —Ā–ł–ľ—É–Ľ–į—Ü–ł–ĺ–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ –Ĺ–į –Ņ—Ä–ĺ—ā–ĺ—ā–ł–Ņ—É –ĺ–ľ–ĺ–≥—É—õ–į–≤–į –Ņ—Ä–ł—Ö–≤–į—ā—ô–ł–≤ –Ņ–ĺ—á–Ķ—ā–Ĺ–ł —Ā–ĺ—Ą—ā–≤–Ķ—Ä –ļ–ĺ–ľ–į–Ĺ–ī–ł –Ľ–Ķ—ā–į –Ī–Ķ–∑ –ł—Ā–Ņ–ł—ā–ł–≤–į—ö–į —É –Ľ–Ķ—ā—É. –Ē–ĺ–Ī–ł—ė–Ķ–Ĺ–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā —Ā–Ķ –Ņ–ĺ—ā–≤—Ä—í—É—ė–Ķ –Ņ–ĺ—É–∑–ī–į–Ĺ–ĺ—ą—õ—É –Ņ—Ä–≤–ł—Ö –Ľ–Ķ—ā–ĺ–≤–į –Ņ—Ä–ĺ—ā–ĺ—ā–ł–Ņ–ĺ–≤–į. –Ę–į—ė —Ā—ā–į–Ĺ–ī–į—Ä–ī —ė–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į –∑–į –ī–į—ô–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā –ĺ–Ņ—ā–ł–ľ–ł–∑–į—Ü–ł—ė–Ķ —Ā–ł—Ā—ā–Ķ–ľ–į –ī–ĺ –ļ–ĺ–Ĺ–į—á–Ĺ–ĺ–≥ —Ä–Ķ—ą–Ķ—ö–į. –ö–ĺ–Ĺ–į—á–Ĺ–ĺ —Ä–Ķ—ą–Ķ—ö–Ķ —Ā–Ķ –Ņ–ĺ—Ā—ā–ł–∂–Ķ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ —É–Ņ–ĺ—Ä–Ķ—í–ł–≤–į—ö–į –ł —Ā—ā–į–Ľ–Ĺ–ĺ–≥ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–≤–į—ö–į –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ĺ–≥ –ĺ–ī–≥–ĺ–≤–ĺ—Ä–į —Ä–Ķ–į–Ľ–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ —É –Ľ–Ķ—ā—É –ł –ĺ–ī–≥–ĺ–≤–ĺ—Ä–į –ļ–ĺ—Ä–ł–≥–ĺ–≤–į–Ĺ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä—É (–≤–ł–ī–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –Ĺ–į —ą–Ķ–ľ–ł –ł—Ā–Ņ–ĺ–ī). –Ę–į—ė –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –ī–ĺ–Ī–ł—ė–į—ö–į –ļ–≤–į–Ľ–ł—ā–Ķ—ā–Ĺ–ĺ–≥ —Ä–Ķ—ą–Ķ—ö–į —Ā–ł—Ā—ā–Ķ–ľ–į –ľ–ĺ–∂–Ķ —Ā–Ķ –Ĺ–į–∑–≤–į—ā–ł —Ö–ł–Ī—Ä–ł–ī–Ĺ–į —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–į, –ĺ–Ņ—ā–ł–ľ–ł–∑–į—Ü–ł—ė–į –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –Ņ–ĺ—Ā—ā–Ķ–Ņ–Ķ–Ĺ–ĺ–≥ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–≤–į—ö–į.
–Ď–Ľ–ĺ–ļ —ą–Ķ–ľ–į –ļ–ĺ—Ä–ł—ą—õ–Ķ–Ĺ–ĺ–≥ —Ā–ł—Ā—ā–Ķ–ľ–į –∑–į –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł–ļ–į—Ü–ł—ė—É –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł—Ö –ļ–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į.[13]
–ě—Ā–Ĺ–ĺ–≤–į –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —ė–Ķ —Ā–Ĺ–ł–ľ–į—ö–Ķ –ĺ–ī–∑–ł–≤–į —Ä–Ķ–į–Ľ–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ł –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä—É –Ľ–Ķ—ā–į, –Ĺ–į –ł–∑–į–Ī—Ä–į–Ĺ–ł —ā–ł–Ņ–ł—á–Ĺ–ł —É–Ľ–į–∑, –∑–į—ā–ł–ľ —ö–ł—Ö–ĺ–≤–ĺ –Ņ–ĺ—Ä–Ķ—í–Ķ—ö–Ķ, —É–ĺ—á–į–≤–į—ö–Ķ –ľ–Ķ—í—É—Ā–ĺ–Ī–Ĺ–Ķ —Ä–į–∑–Ľ–ł–ļ–Ķ –ł –Ņ—Ä–Ķ–ī—É–∑–ł–ľ–į—ö–Ķ –ļ–ĺ—Ä–Ķ–ļ—Ü–ł—ė–į –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–į—Ä–Ĺ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į –ł –∑–į–ļ–ĺ–Ĺ–į —É–Ņ—Ä–į–≤—ô–į—ö–į —É —Ā–ľ–Ķ—Ä—É —Ā–ľ–į—ö–Ķ—ö–į —ā–ł—Ö —Ä–į–∑–Ľ–ł–ļ–į. –°–Ĺ–ł–ľ—ô–Ķ–Ĺ–ł –ĺ–ī–∑–ł–≤, –Ņ—Ä–Ķ–ļ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł—Ö –ľ–Ķ—ā–ĺ–ī–į –į–Ĺ–į–Ľ–ł–∑–Ķ, —Ā–Ľ—É–∂–ł –ł –∑–į –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł–ļ–į—Ü–ł—ė—É —Ā—ā–≤–į—Ä–Ĺ–ł—Ö —Ā–į–Ī–ł—Ä–į–ļ–į (–≥—Ä–į–ī–ł—ė–Ķ–Ĺ–į—ā–į, –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į) –ĺ–ī–≥–ĺ–≤–į—Ä–į—ė—É—õ–Ķ –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ–Ķ –ļ–į–ĺ —ą—ā–ĺ —ė–Ķ –ī–į—ā–ĺ —É —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–ł –∑–į –ĺ—ā–Ņ–ĺ—Ä. –Ę–ł–ľ –Ņ—É—ā–Ķ–ľ —Ā—É –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł –Ņ–ĺ–ī–į—Ü–ł –ļ–ĺ—Ä–ł–≥—É—ė—É —É –Ī–į–∑–ł –Ņ–ĺ–ī–į—ā–į–ļ–į –ł —É —Ä–Ķ–Ľ–Ķ–≤–į–Ĺ—ā–Ĺ–ł–ľ –Ņ—Ä–ĺ—Ä–į—á—É–Ĺ–ł–ľ–į. –£–ļ–Ľ–į—ö–į—ö–Ķ —Ä–į–∑–Ľ–ł–ļ–Ķ —É –ĺ–ī–∑–ł–≤—É —Ä–Ķ–į–Ľ–ł–∑—É—ė–Ķ —Ā–Ķ —Ā–į –Ņ–ĺ–Ņ—Ä–į–≤–ļ–ĺ–ľ –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–į—ā–ļ–į –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–į—Ä–Ĺ–ĺ–≥ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į –ļ—Ä–ĺ–∑ –ļ–ĺ—Ä–Ķ–ļ—Ü–ł—ė—É —ö–Ķ–≥–ĺ–≤–ł—Ö –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ–į—ā–į —Ā–į –Ĺ–ĺ–≤–ĺ–ī–ĺ–Ī–ł—ė–Ķ–Ĺ–ł–ľ –Ņ–ĺ–ī–į—Ü–ł–ľ–į –ł–∑ —Ā–Ĺ–ł–ľ–ļ–į –ĺ–ī–∑–ł–≤–į —Ä–Ķ–į–Ľ–Ĺ–ĺ–≥ –į–≤–ł–ĺ–Ĺ–į —É –Ľ–Ķ—ā—É. –ö–ĺ—Ä–Ķ–ļ—Ü–ł—ė–Ķ —Ā–Ķ –Ņ—Ä–ł–ĺ—Ä–ł—ā–Ķ—ā–Ĺ–ĺ —Ā–Ņ—Ä–ĺ–≤–ĺ–ī–Ķ –Ĺ–į –ľ–Ķ—Ā—ā–ł–ľ–į –≤–Ķ—õ–ł—Ö —Ä–į–∑–Ľ–ł–ļ–į ‚Äě–ĺ–ī–∑–ł–≤–į‚Äú —Ä–Ķ–į–Ľ–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ł –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä—É. –Ě–į —ā–į—ė –Ĺ–į—á–ł–Ĺ —Ā–Ķ –Ņ–ĺ—Ā—ā—É–Ņ–Ĺ–ĺ –į–∂—É—Ä–ł—Ä–į –Ī–į–∑–į –Ņ–ĺ–ī–į—ā–į–ļ–į –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–į—Ä–Ĺ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į –ł —Ā–į–≥–Ľ–į—Ā–Ĺ–ĺ —ā–ĺ–ľ–Ķ —Ā–Ķ –Ņ–ĺ–Ĺ–ĺ–≤–ĺ —É—Ā–ļ–Ľ–į—í—É—ė—É –∑–į–ļ–ĺ–Ĺ–ł —É–Ņ—Ä–į–≤—ô–į—ö–į.
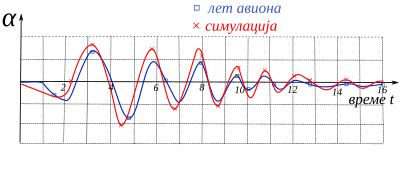 –£–Ņ–ĺ—Ä–Ķ–ī–Ĺ–ł –ĺ–ī–∑–ł–≤–ł —Ā—ā–≤–į—Ä–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ —É –Ľ–Ķ—ā—É –ł —Ā–ł–ľ—É–Ľ–į—Ü–ł–ĺ–Ĺ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į —Ä–į–∑–≤–ĺ—ė–Ĺ–ĺ–ľ —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä—É.
–£–Ņ–ĺ—Ä–Ķ–ī–Ĺ–ł –ĺ–ī–∑–ł–≤–ł —Ā—ā–≤–į—Ä–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ —É –Ľ–Ķ—ā—É –ł —Ā–ł–ľ—É–Ľ–į—Ü–ł–ĺ–Ĺ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į —Ä–į–∑–≤–ĺ—ė–Ĺ–ĺ–ľ —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä—É.
–ú–Ķ—ā–ĺ–ī–ĺ–ľ —É–∑–į—Ā—ā–ĺ–Ņ–Ĺ–ĺ–≥ –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–≤–į—ö–į –ī–ĺ–Ľ–į–∑–ł —Ā–Ķ –ī–ĺ –∑–į–ī–ĺ–≤–ĺ—ô–į–≤–į—ė—É—õ–Ķ–≥ —Ä–Ķ—ą–Ķ—ö–į, —É—Ā–Ņ–ĺ—Ā—ā–į–≤—ô–į —Ā–Ķ —Ā—ā–į–Ĺ–ī–į—Ä–ī –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –Ņ—Ä–Ķ–ľ–į –≤–į–∂–Ķ—õ–ł–ľ –Ņ—Ä–ĺ–Ņ–ł—Ā–ł–ľ–į, –Ĺ–į–ľ–Ķ–Ĺ–ł –ł –∑–į—Ö—ā–Ķ–≤–ł–ľ–į –Ņ–ł–Ľ–ĺ—ā–į.
–ź–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł –ĺ—ā–Ņ–ĺ—Ä, –ľ–ĺ–∂–Ķ —Ā–Ķ —Ä–į–∑–Ľ–ĺ–∂–ł—ā–ł –Ĺ–į —á–Ľ–į–Ĺ–ĺ–≤–Ķ:[1]

–ö–į–ĺ —ą—ā–ĺ —ė–Ķ –Ņ—Ä–ł–Ľ–į–∑ –∑–į –ļ—Ä–Ķ—ā–į—ö–Ķ –ī—É–∂ x –ĺ—Ā–Ķ, –ł—Ā—ā–ĺ –≤–į–∂–ł –ł –∑–į —Ā–≤–Ķ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ķ —Ā–Ľ–ĺ–Ī–ĺ–ī–Ķ –ļ—Ä–Ķ—ā–į—ö–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ, –ī—É–∂ —Ā–≤–Ķ —ā—Ä–ł –ĺ—Ā–Ķ –ł –∑–į —Ä–ĺ—ā–į—Ü–ł—ė—É –ĺ–ļ–ĺ —ö–ł—Ö.
–£ –Ņ—Ä–Ķ—ā—Ö–ĺ–ī–Ĺ–ĺ—ė —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–ł —ė–Ķ –ī–į—ā–į –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā –ļ–ĺ–Ķ—Ą–ł—Ü–ł—ė–Ķ–Ĺ—ā–į –ĺ—ā–Ņ–ĺ—Ä–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ —Ā–į –ī–ĺ–Ņ—Ä–ł–Ĺ–ĺ—Ā–ĺ–ľ —ö–Ķ–≥–ĺ–≤–ĺ–≥ —Ä–į—Ā—ā–į —É—Ā–Ľ–Ķ–ī –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ –Ĺ–į–Ņ–į–ī–Ĺ–ĺ–≥ —É–≥–Ľ–į, –ĺ—ā–ļ–Ľ–ĺ–Ĺ–į –ļ–ĺ–ľ–į–Ĺ–ī–Ĺ–Ķ –Ņ–ĺ–≤—Ä—ą–Ĺ–Ķ –ł –Ņ—Ä–ł–≥—É—ą–Ķ—ö–į –∑–Ī–ĺ–≥ —É–≥–į–ĺ–Ĺ–Ķ –Ī—Ä–∑–ł–Ĺ–Ķ —Ä–ĺ—ā–į—Ü–ł—ė–Ķ.
–ď—Ä–į–ī–ł—ė–Ķ–Ĺ—ā–ł –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ–ĺ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—ô–ł–≤–ĺ—ė —Ā—É –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł. –ü–ĺ –ł—Ā—ā–ĺ–ľ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—É —ė–Ķ –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł–ļ–ĺ–≤–į–Ĺ –ł –ľ–ĺ–ľ–Ķ–Ĺ—ā –Ņ—Ä–ĺ–Ņ–ł—ö–į—ö–į, –Ņ–į –ł –ĺ—Ā—ā–į–Ľ–Ķ –ļ–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–Ķ:[1]

–ě–≤–ĺ–ľ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ —Ā–Ķ —É—Ā–Ņ–Ķ—ą–Ĺ–ĺ –į–∂—É—Ä–ł—Ä–į–Ĺ–į –Ī–į–∑–į –Ņ–ĺ–ī–į—ā–į–ļ–į –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ—Ä–Ĺ–ĺ–≥ –ľ–ĺ–ī–Ķ–Ľ–į. –ö–ĺ—Ä–ł—ą—õ–Ķ–Ĺ–ł –į–Ľ–≥–ĺ—Ä–ł—ā–į–ľ –≥—Ä–Ķ—ą–ļ–Ķ —É –ĺ–ī–∑–ł–≤—É —Ä–Ķ–į–Ľ–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ł –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į–Ĺ–ĺ–≥ –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–į—Ä–Ĺ–ĺ–≥ –Ņ–į–ļ–Ķ—ā–į —Ā–≤–ĺ–ī–ł —Ä–į–∑–Ľ–ł–ļ—É –Ĺ–į –ľ–ł–Ĺ–ł–ľ—É–ľ. –Ę–ł–ľ–Ķ —ė–Ķ –Ĺ–į–Ņ—Ä–į–≤—ô–Ķ–Ĺ–į —Ä–Ķ–į–Ľ–Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į –∑–į –ł–∑–Ī–ĺ—Ä –ĺ–Ņ—ā–ł–ľ–į–Ľ–Ĺ–ł—Ö –∑–į–ļ–ĺ–Ĺ–į —É–Ņ—Ä–į–≤—ô–į—ö–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–ĺ–ľ, —ā–ĺ —ė–Ķ—Ā—ā, –ĺ–Ī–Ķ–∑–Ī–Ķ—í–Ķ–Ĺ–į —ė–Ķ ‚Äě–Ņ–į–ľ–Ķ—ā‚Äú –ļ–ĺ–ľ–į–Ĺ–ī–Ĺ–ĺ–ľ —Ā–ł—Ā—ā–Ķ–ľ—É –∑–į –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ —É–Ņ—Ä–į–≤—ô–į—ö–Ķ —Ā —ö–ĺ–ľ —É —Ü–Ķ–Ľ–ĺ—ė –į–Ĺ–≤–Ķ–Ľ–ĺ–Ņ–ł –Ľ–Ķ—ā–į –ł —É —Ā–≤–ł–ľ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł—ė–į–ľ–į.[13]
–£–Ņ–ĺ—ā—Ä–Ķ–Ī–į
–õ–ł–Ĺ–Ķ–į—Ä–ł–∑–į—Ü–ł—ė–į —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –ļ—Ä–Ķ—ā–į—ö–į –ł —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–į
–£–≤–ĺ—í–Ķ—ö–Ķ–ľ –Ņ–ĺ—ė–ľ–ĺ–≤–į –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į (—É–Ņ—Ä–ĺ—ą—õ–į–≤–į—ö–Ķ–ľ —Ā–į–ľ–ĺ —Ā –Ņ—Ä–≤–ĺ—Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł–ľ –ī–ł—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä–į—ö–Ķ–ľ) –ł–∑–≤—Ä—ą–Ķ–Ĺ–į —ė–Ķ –Ľ–ł–Ĺ–Ķ–į—Ä–ł–∑–į—Ü–ł—ė–į —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –ļ—Ä–Ķ—ā–į—ö–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ. –°–ł–ľ—É–Ľ–į—Ü–ł—ė–į –Ľ–Ķ—ā–į —Ā–Ķ –∑–į—Ā–Ĺ–ł–≤–į –Ĺ–į —ā–ĺ—ė –Ľ–ł–Ĺ–Ķ–į—Ä–ł–∑–į—Ü–ł—ė–ł —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į –ļ—Ä–Ķ—ā–į—ö–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–į, —ą—ā–ĺ —Ā–Ķ –∑–į—Ā–Ĺ–ł–≤–į –Ĺ–į –Ņ—Ä–Ķ—ā–Ņ–ĺ—Ā—ā–į–≤—Ü–ł –ľ–į–Ľ–ł—Ö –Ņ–ĺ—Ä–Ķ–ľ–Ķ—õ–į—ė–į. –Ę–į –į–Ņ—Ä–ĺ–ļ—Ā–ł–ľ–į—Ü–ł—ė–į –∑–į–ī–ĺ–≤–ĺ—ô–į–≤–į –Ņ–ĺ—ā—Ä–Ķ–Ī–Ķ –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–į. –£ —Ü–ł—ô—É –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į—á–ļ–ĺ–≥ –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į—ö–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ (—É–ļ—ô—É—á—É—ė—É—õ–ł –ł –ļ–ĺ–ľ–į–Ĺ–ī–Ķ –Ľ–Ķ—ā–į), —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–ĺ–ľ —Ā–Ķ –ļ—Ä–Ķ—õ–Ķ –ĺ–ī —Ā–į–ľ–ĺ–≥ –Ņ–ĺ—á–Ķ—ā–ļ–į –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–į, —Ā–į –Ņ–ĺ—á–Ķ—ā–Ĺ–ł–ľ –Ņ–ĺ–ī–į—Ü–ł–ľ–į –∑–į –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–Ķ, –ľ–į—Ā—É –ł –ľ–ĺ–ľ–Ķ–Ĺ—ā–Ķ –ł–Ĺ–Ķ—Ä—Ü–ł—ė–Ķ –ł—ā–ī.
–°–ł–ľ—É–Ľ–į—Ü–ł—ė–į –Ľ–Ķ—ā–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –ĺ–ľ—É–≥—É—õ—É—ė–Ķ –Ņ—Ä–ĺ—ė–Ķ–ļ–į—ā —Ä–į–∑–≤–ĺ—ė–Ĺ–ĺ–≥ —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä–į, —á–ł—ė–ł —ė–Ķ –ī–ĺ–Ņ—Ä–ł–Ĺ–ĺ—Ā –ĺ–Ņ–ł—Ā–į–Ĺ —É –Ņ—Ä–Ķ—ā—Ö–ĺ–ī–Ĺ–ĺ–ľ –Ņ–ĺ–≥–Ľ–į–≤—ô—É –ł —É—á–ł–Ľ–į –∑–į –ĺ–Ī—É–ļ—É –Ņ–ł–Ľ–ĺ—ā–į –Ĺ–į –∑–Ķ–ľ—ô–ł (—Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä–į –Ľ–Ķ—ā–į).[1][13]
–°–ł–ľ—É–Ľ–į—ā–ĺ—Ä–ł –Ľ–Ķ—ā–į –∑–į –ĺ–Ī—É–ļ—É –Ņ–ł–Ľ–ĺ—ā–į
 –í–ĺ—ė–Ĺ–ł —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä –Ľ–Ķ—ā–į —É –®–≤–į—ė—Ü–į—Ä—Ā–ļ–ĺ—ė.
–í–ĺ—ė–Ĺ–ł —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä –Ľ–Ķ—ā–į —É –®–≤–į—ė—Ü–į—Ä—Ā–ļ–ĺ—ė.
–°–ł–ľ—É–Ľ–į—ā–ĺ—Ä –Ľ–Ķ—ā–į —ė–Ķ —É—Ä–Ķ—í–į—ė –ļ–ĺ—ė–ł —Ā–ł–ľ—É–Ľ–ł—Ä–į —É—Ā–Ľ–ĺ–≤–Ķ –ł –ļ–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–Ķ –Ľ–Ķ—ā–į –≤–į–∑–ī—É—Ö–ĺ–Ņ–Ľ–ĺ–≤–į –ł —Ā—Ä–Ķ–ī–ł–Ĺ–Ķ —É –ļ–ĺ—ė–ĺ—ė —Ā–Ķ –ł—Ā—ā–ł —Ä–Ķ–į–Ľ–ł–∑—É—ė–Ķ. –Ě–į —ö–Ķ–ľ—É —Ā–Ķ –≤—Ä—ą–ł –ĺ–Ī—É–ļ–į, –Ņ—Ä–ĺ–≤–Ķ—Ä–į –ł —ā—Ä–Ķ–Ĺ–į–∂–į –Ņ–ł–Ľ–ĺ—ā–į, –Ĺ–į –∑–Ķ–ľ—ô–ł, —Ā–į —á–ł–ľ–Ķ —Ā–Ķ —É—ą—ā–Ķ–ī–Ķ –≤–Ķ–Ľ–ł–ļ–į —Ą–ł–Ĺ–į–Ĺ—Ā–ł—ė—Ā–ļ–į —Ā—Ä–Ķ–ī—Ā—ā–≤–į. –£–ļ—ô—É—á—É—ė—É—õ–ł —Ä–Ķ–Ņ–Ľ–ł—Ü–ł—Ä–į—ö–Ķ —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į, –ļ–ĺ—ė–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—ô–į—ė—É —Ą–ł–∑–ł–ļ–į–Ľ–Ĺ–ĺ—Ā—ā –Ľ–Ķ—ā–į –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ, —Ä–Ķ–į–ļ—Ü–ł—ė—É –Ĺ–į –Ņ—Ä–ł–ľ–Ķ–Ĺ—É —É–Ņ—Ä–į–≤—ô–į—á–ļ–ł—Ö –ļ–ĺ–ľ–į–Ĺ–ī–ł, –Ķ—Ą–Ķ–ļ—ā–Ķ —Ā–≤–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ–į –≤–į–∑–ī—É—Ö–ĺ–Ņ–Ľ–ĺ–≤–į –ł —Ä–Ķ–į–ļ—Ü–ł—ė—É –Ĺ–į —Ā–Ņ–ĺ—ô–Ĺ–Ķ —Ą–į–ļ—ā–ĺ—Ä–Ķ, –ļ–į–ĺ —ą—ā–ĺ —Ā—É –≥—É—Ā—ā–ł–Ĺ–į –≤–į–∑–ī—É—Ö–į, —ā—É—Ä–Ī—É–Ľ–Ķ–Ĺ—Ü–ł—ė–į, —É–ī–į—Ä–ł –≤–Ķ—ā—Ä–į, –Ņ–į–ī–į–≤–ł–Ĺ–Ķ –ł—ā–ī. (—Ā–Ņ–ĺ—ô–Ĺ–Ķ –Ņ–ĺ—Ä–Ķ–ľ–Ķ—õ–į—ė–Ķ). –°–ł–ľ—É–Ľ–į—ā–ĺ—Ä–ł –Ľ–Ķ—ā–į —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–Ķ —É —ā–ĺ–ļ—É —ą–ļ–ĺ–Ľ–ĺ–≤–į—ö–į –ł –ĺ–ī—Ä–∂–į–≤–į—ö–Ķ —ā—Ä–Ķ–Ĺ–į–∂–Ķ –Ņ–ł–Ľ–ĺ—ā–į. –£ –ł–Ĺ–∂–Ķ—ö–Ķ—Ä—Ā—ā–≤—É —Ā–Ķ –ļ–ĺ—Ä–ł—Ā—ā–ł —É —ā–ĺ–ļ—É —Ä–į–∑–≤–ĺ—ė–į –į–≤–ł–ĺ–Ĺ–į, –Ņ–ĺ—Ā–Ķ–Ī–Ĺ–ĺ –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–į —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł, —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā–ł –ł —Ā–ł—Ā—ā–ľ–į –ļ–ĺ–ľ–į–Ĺ–ī–ł –Ľ–Ķ—ā–į, —ą—ā–ĺ —ė–Ķ –ĺ–Ĺ–į–≤–Ķ–ī–Ķ–Ĺ–ĺ —É –Ņ—Ä–Ķ—ā—Ö–ĺ–ī–Ĺ–ĺ–ľ –Ņ–ĺ–≥–Ľ–į–≤—ô—É.[14]
–°–ł–ľ—É–Ľ–į—ā–ĺ—Ä–ł –Ľ–Ķ—ā–į —Ā–į–ī—Ä–∂–Ķ —Ä–į–∑–Ľ–ł—á–ł—ā–Ķ –≤—Ä—Ā—ā–Ķ —Ö–į—Ä–ī–≤–Ķ—Ä–į –ł —Ā–ĺ—Ą—ā–≤–Ķ—Ä–į, —É –∑–į–≤–ł—Ā–Ĺ–ĺ—Ā—ā–ł –ĺ–ī –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į—ö–į –ī–Ķ—ā–į—ô–į –ł —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–Ķ —Ä–į–ī—ö–ł. –ü—Ä–ĺ—ė–Ķ–ļ—ā–ł —Ā–į–ī—Ä–∂–Ķ –≤–į—Ä–ł—ė–į–Ĺ—ā–Ķ —É —Ä–į—Ā–Ņ–ĺ–Ĺ—É –ĺ–ī —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–Ķ –Ĺ–į –Ľ–į–Ņ—ā–ĺ–Ņ—É, –Ĺ–į –Ī–į–∑–ł –ľ–ĺ–ī–Ķ–Ľ–į —Ā–ł—Ā—ā–Ķ–ľ–į –≤–į–∑–ī—É—Ö–ĺ–Ņ–Ľ–ĺ–≤–į, –ī–ĺ –Ņ–ĺ—ā–Ņ—É–Ĺ–Ķ —Ä–Ķ–Ņ–Ľ–ł–ļ–Ķ –ļ–į–Ī–ł–Ĺ–Ķ –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–Ķ –∑–į –Ņ–ĺ—á–Ķ—ā–Ĺ–ĺ —É–Ņ–ĺ–∑–Ĺ–į–≤–į—ö–Ķ, –Ņ–į –ī–ĺ –Ņ–ĺ—ā–Ņ—É–Ĺ–ĺ —Ä–Ķ–į–Ľ–Ĺ–ł—Ö —Ā–ł–ľ—É–Ľ–į—Ü–ł—ė–į –ļ–į–Ī–ł–Ĺ–Ķ, –ļ–ĺ–ľ–į–Ĺ–ī–ł –Ľ–Ķ—ā–į –ł –ĺ—Ā—ā–į–Ľ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ–į –≤–į–∑–ī—É—Ö–ĺ–Ņ–Ľ–ĺ–≤–į, –∑–į –≤–ł—ą—É –ł –ļ–ĺ–ľ–Ņ–Ľ–Ķ—ā–Ĺ—É –ĺ–Ī—É–ļ—É –Ņ–ł–Ľ–ĺ—ā–į. –Ě–į—ė–≤–ł—ą–ł –Ĺ–ł–≤–ĺ —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä–į –Ľ–Ķ—ā–į —Ā—É –∑–į –ĺ–Ī—É–ļ—É –Ņ–ł–Ľ–ĺ—ā–į –Ņ—É—ā–Ĺ–ł—á–ļ–ł—Ö –į–≤–ł–ĺ–Ĺ–į, –į –∑–į –ĺ–Ī—É–ļ—É –≤–ĺ—ė–Ĺ–ł—Ö –Ņ–ł–Ľ–ĺ—ā–į —ė–Ķ –Ĺ–Ķ—ą—ā–ĺ –Ĺ–ł–∂–ł. –Ě–į –Ņ—Ä–ł–ľ–Ķ—Ä, –ľ–Ķ—í—É–Ĺ–į—Ä–ĺ–ī–Ĺ–ł –≤–ł—ą–ł –Ĺ–ł–≤–ĺ –∑–į—Ö—ā–Ķ–≤–į –ļ—Ä–Ķ—ā–į—ö–į –Ņ–Ľ–į—ā—Ą–ĺ—Ä–ľ–Ķ —Ā–į –ļ–į–Ī–ł–Ĺ–ĺ–ľ —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä–į, —É –ĺ–ļ–≤–ł—Ä—É —Ā–≤–ł—Ö —ą–Ķ—Ā—ā —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł —Ā–Ľ–ĺ–Ī–ĺ–ī–Ķ –ł –≤–ł–∑—É–Ķ–Ľ–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ĺ–ľ, —É –ĺ–ļ–≤–ł—Ä—É –≤–ł–ī—ô–ł–≤–ĺ—Ā—ā–ł –ĺ–ī 150 —Ö 40, –∑–į —Ü–Ķ–Ľ—É –Ņ–ĺ–Ņ—É–Ľ–į—Ü–ł—ė—É –Ņ–ł–Ľ–ĺ—ā–į. –í–ĺ—ė–Ĺ–ł —Ā–ł–ľ—É–Ľ–į—ā–ĺ—Ä–ł –Ľ–Ķ—ā–į –ł–ľ–į—ė—É –≤–ł—ą–Ķ –≤–į—Ä–ł—ė–į—Ü–ł—ė–į —É –Ņ—Ä–ĺ—ė–Ķ–ļ—ā–ĺ–≤–į—ö—É.[15][16]
–í–ł–ī–ł —ė–ĺ—ą
–†–Ķ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–Ķ
- ^ –į –Ī –≤ –≥ –ī —í –Ķ –Ě–Ķ–Ĺ–į–ī–ĺ–≤–ł—õ, –ú–ł—Ä–ĺ—Ā–Ľ–į–≤ (1971). ‚Äě–ź–Ķ—Ä–ĺ–ī–ł–Ĺ–į–ľ–ł—á–ļ–ł –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–ł‚ÄĚ. –°—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā –Ľ–Ķ—ā–Ķ–Ľ–ł—Ü–į (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: —Ā—Ä–Ņ—Ā–ļ–ł)). –Ď–Ķ–ĺ–≥—Ä–į–ī. 741: 668‚ÄĒ712.
- ^ –†–Ķ–Ĺ–ī—É–Ľ–ł—õ, –ó–Ľ–į—ā–ļ–ĺ (1987). ‚Äě–£–≤–ĺ–ī —É —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā –ł —É–Ņ—Ä–į–≤—ô–ł–≤–ĺ—Ā—ā‚ÄĚ. –ú–Ķ—Ö–į–Ĺ–ł–ļ–į –Ľ–Ķ—ā–į (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: —Ā—Ä–Ņ—Ā–ļ–ł)). –Ď–Ķ–ĺ–≥—Ä–į–ī. 615: 273‚ÄĒ279.
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, 1950.
- ^ –†–Ķ–Ĺ–ī—É–Ľ–ł—õ, –ó–Ľ–į—ā–ļ–ĺ (1987). ‚Äě–Ē–Ķ—Ä–ł–≤–į—ā–ł–≤–ł –ł –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ł —É —ė–Ķ–ī–Ĺ–į—á–ł–Ĺ–į–ľ–į –ļ—Ä–Ķ—ā–į—ö–į‚ÄĚ. –ú–Ķ—Ö–į–Ĺ–ł–ļ–į –Ľ–Ķ—ā–į (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: —Ā—Ä–Ņ—Ā–ļ–ł)). –Ď–Ķ–ĺ–≥—Ä–į–ī. 615: 457‚ÄĒ459.
- ^ ‚ÄěLongitudinal stability derivatives‚ÄĚ (PDF) (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: –Ķ–Ĺ–≥–Ľ–Ķ—Ā–ļ–ł)). aerostudents.com. –ź—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–ĺ –ł–∑ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–į (pdf) 23. 08. 2013. –≥. –ü—Ä–ł—Ā—ā—É–Ņ—ô–Ķ–Ĺ–ĺ 19. 8. 2013. ‚ÄěLongitudinal stability derivatives‚ÄĚ
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, p 65, 1950.
- ^ –†–Ķ–Ĺ–ī—É–Ľ–ł—õ, –ó–Ľ–į—ā–ļ–ĺ (1987). ‚Äě–°—É–ľ–ł—Ä–į—ö–Ķ –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į –ł –ļ–ĺ–Ķ—Ą–ł—Ü–ł—ė–Ķ–Ĺ–į—ā–į –ľ–ĺ–ľ–Ķ–Ĺ–į—ā–į –≤–į—ô–į—ö–į –ł —Ā–ļ—Ä–Ķ—ā–į—ö–į‚ÄĚ. –ú–Ķ—Ö–į–Ĺ–ł–ļ–į –Ľ–Ķ—ā–į (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: —Ā—Ä–Ņ—Ā–ļ–ł)). –Ď–Ķ–ĺ–≥—Ä–į–ī. 615: 433‚ÄĒ4436.
- ^ ‚ÄěLateral stability derivatives‚ÄĚ (PDF) (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: –Ķ–Ĺ–≥–Ľ–Ķ—Ā–ļ–ł)). aerostudents.com. –ź—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–ĺ –ł–∑ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–į (pdf) 23. 08. 2013. –≥. –ü—Ä–ł—Ā—ā—É–Ņ—ô–Ķ–Ĺ–ĺ 19. 8. 2013. ‚ÄěLateral stability derivatives‚ÄĚ
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, p 83, 1950.
- ^ Mesure des derivees aerodynamiquesen eceouulement transonique et supersonique, Sherer, Publication N0 104, 1962.g.
- ^ –°. –ü—É—Ā—ā–ł—ö–į, –°—ā—É–ī–ł—ė–į –ī–Ķ—Ä–ł–≤–į—ā–ł–≤–į –Ņ–ĺ–Ņ—Ä–Ķ—á–Ĺ–ĺ-—Ā–ľ–Ķ—Ä–Ĺ–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ĺ—Ā—ā–ł , –°–į–ĺ–Ņ—ą—ā–Ķ—ö–Ķ –í–Ę–ė-–į, 1968.
- ^ –°. –ü—É—Ā—ā–ł—ö–į, –ú–Ķ—Ä–Ķ—ö–Ķ –Ķ—Ą–ł–ļ–į—Ā–Ĺ–ĺ—Ā—ā–ł –ļ—Ä–ł–Ľ–į—Ü–į –į–≤–ł–ĺ–Ĺ–į —É –į–Ķ—Ä–ĺ—ā—É–Ĺ–Ķ–Ľ—É , –í–ĺ—ė–Ĺ–ĺ—ā–Ķ—Ö–Ĺ–ł—á–ļ–ł –≥–Ľ–į—Ā–Ĺ–ł–ļ, 1970.
- ^ –į –Ī –≤ Renzo Bava; Graham T. Hoare; Gabriel Garcia-Mesuro; Hans-Christoph Oelker. ‚ÄěRecent Experiences on Aerodynamic Parameter Identification for EUROFIGHTER at Alenia, British Aerospace, CASA and Daimler-Benz Aerospace‚ÄĚ (PDF) (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: –Ķ–Ĺ–≥–Ľ–Ķ—Ā–ļ–ł)). –ź—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–ĺ –ł–∑ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–į (PDF) 03. 03. 2012. –≥. –ü—Ä–ł—Ā—ā—É–Ņ—ô–Ķ–Ĺ–ĺ 18. 8. 2013. ‚Äě–ė–ī–Ķ–Ĺ—ā–ł—Ą–ł–ļ–į—Ü–ł—ė–į –į–Ķ—Ä–ĺ–ī–ł–Ĺ–į—á–ļ–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā–į—Ä–į —ā–į—ė—Ą—É–Ĺ–į‚ÄĚ
- ^ ‚Äě–ü–ł–Ľ–ĺ—ā–į–∂–Ĺ—č–Ļ —ā—Ä–Ķ–Ĺ–į–∂–Ķ—Ä —Ā–į–ľ–ĺ–Ľ–Ķ—ā–į SSJ 100 –≥–ĺ—ā–ĺ–≤ –ļ –ĺ–Ī—É—á–Ķ–Ĺ–ł—é —Ä–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–ł—Ö –Ņ–ł–Ľ–ĺ—ā–ĺ–≤‚ÄĚ (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: —Ä—É—Ā–ļ–ł)). ato.ru. 22. 11. 2011. –ü—Ä–ł—Ā—ā—É–Ņ—ô–Ķ–Ĺ–ĺ 11. 8. 2013. ‚Äě–ü–ł–Ľ–ĺ—ā–į–∂–Ĺ—č–Ļ —ā—Ä–Ķ–Ĺ–į–∂–Ķ—Ä —Ā–į–ľ–ĺ–Ľ–Ķ—ā–į SSJ 100 –≥–ĺ—ā–ĺ–≤ –ļ –ĺ–Ī—É—á–Ķ–Ĺ–ł—é —Ä–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–ł—Ö –Ņ–ł–Ľ–ĺ—ā–ĺ–≤‚ÄĚ
- ^ ‚ÄěASME International The Link Flight Trainer‚ÄĚ (PDF) (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: –Ķ–Ĺ–≥–Ľ–Ķ—Ā–ļ–ł)). files.asme.org. –ź—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–ĺ –ł–∑ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–į (pdf) 17. 12. 2011. –≥. –ü—Ä–ł—Ā—ā—É–Ņ—ô–Ķ–Ĺ–ĺ 19. 8. 2013. ‚ÄěASME International The Link Flight Trainer‚ÄĚ
- ^ ‚ÄěU.S. Air Force Fact Sheet LINK TRAINER‚ÄĚ (–Ĺ–į —ė–Ķ–∑–ł–ļ—É: (—ė–Ķ–∑–ł–ļ: –Ķ–Ĺ–≥–Ľ–Ķ—Ā–ļ–ł)). nationalmuseum.af.mil. –ź—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–ĺ –ł–∑ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–į 24. 01. 2012. –≥. –ü—Ä–ł—Ā—ā—É–Ņ—ô–Ķ–Ĺ–ĺ 19. 8. 2013. ‚ÄěLINK TRAINER‚ÄĚ
–°–Ņ–ĺ—ô–į—ą—ö–Ķ –≤–Ķ–∑–Ķ