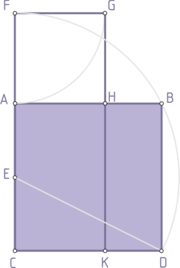
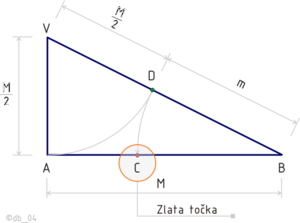
Zlati rez
|
Read other articles:

日本の行政機関公害等調整委員会こうがいとうちょうせいいいんかいEnvironmental Dispute Coordination Commission 公害等調整委員会が設置されている中央合同庁舎第4号館役職委員長 永野厚郎組織上部組織 総務省内部部局 事務局概要法人番号 1000012020002 所在地 〒100-0013東京都千代田区霞が関3丁目1番1号※令和7年度以降、中央合同庁舎第5号館別館に移転予定[1]。北緯35度40分2...

Lizzie Holden Lizzie Holden na de Amstel Gold Race 2022 Persoonlijke informatie Volledige naam Elizabeth Rose Rebecca Holden Geboortedatum 12 september 1997 Geboorteplaats Douglas (Man), Verenigd Koninkrijk Sportieve informatie Huidige ploeg UAE Team ADQ Ploegen 2017-20192020-202120222023 Drops Cycling TeamBizkaia-DurangoLe Col-WahooUAE Team ADQ Beste prestaties Amstel Gold Race 18e (2022) Portaal Wielersport Elizabeth Rose Rebecca Lizzie Holden (Douglas, 12 september 1997) is ee...

Фукунісі Такасі Фукунісі Такасі Особисті дані Повне ім'я Фукунісі Такасі Народження 1 вересня 1976(1976-09-01) (47 років) Ехіме, Японія Зріст 181 см Вага 77 кг Громадянство Японія Позиція Півзахисник Професіональні клуби* Роки Клуб Ігри (голи) 1995-200620072008 «Джубіло Івата�...

قاعة مشاهير الطب الكنديين الاختصار CMHF البلد كندا المقر الرئيسي لندن، مقاطعة أونتاريو، كندا تاريخ التأسيس 1994 منطقة الخدمة لندن، أونتاريو، كندا الموقع الرسمي الموقع الرسمي الإحداثيات 42°59′06″N 81°14′44″W / 42.9851°N 81.2456°W / 42.9851; -81.2456 تعديل مصدري - تعديل قاعة...

Cet article est une ébauche concernant la Hongrie et l’héraldique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Article principal : Armorial des localités de Hongrie. Cette page donne les armoiries (figures et blasonnements) des localités du comitat de Baranya. Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Abaliget Blason Détails Le statut officiel du blason reste à ...

US federal law Competition law Basic concepts History of competition law Monopoly and oligopoly Coercive monopoly Natural monopoly Barriers to entry Herfindahl–Hirschman Index Market concentration Market power SSNIP test Relevant market Merger control Anti-competitive practices Monopolization Collusion Formation of cartels Price fixing (cases) Bid rigging Tacit collusion Product bundling and tying Refusal to deal Group boycott Essential facilities Exclusive dealing Dividing territories Pred...

The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (October 2022) (Learn how and when to remove this template message) Typical hairstyles of the early 50s shown here on Fernando Lamas and Danielle Darrieux In the Western world, the 1950s were a decade known for experimentation with new styles and culture. Following World War II and the austeri...

Music genre British soulStylistic originsSoulrhythm and bluesgospelbluesblues rockCultural originsEarly 1960s, United KingdomTypical instrumentsStringshornsguitarvocalsDerivative formsNorthern soul British soul, Brit soul, or (in a US context) the British soul invasion, is soul music performed by British artists. Soul has been a major influence on British popular music since the 1960s, and American soul was extremely popular among some youth subcultures, such as mods, skinheads, and the North...

علي السلطان معلومات شخصية الاسم الكامل علي عبد الله السلطان الميلاد 27 أكتوبر 2001 (العمر 22 سنة)المملكة العربية السعودية مركز اللعب ظهير أيسر الجنسية السعودية معلومات النادي النادي الحالي نادي الفيصلي الرقم 66 مسيرة الشباب سنوات فريق نادي الفيصلي المسيرة الاحترافية1 سنوا�...

The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (December 2022) (Learn how and when to remove this template message)Medical equipment and devices The medical–industrial complex is a network of interactions between pharmaceutical corporations, health care personnel, and medical conglomerates to supply health care-related products and services for a profit.[1][2]...

British radio astronomer (1924–2021) Antony HewishFRS FInstPBorn(1924-05-11)11 May 1924Fowey, Cornwall, EnglandDied13 September 2021(2021-09-13) (aged 97)NationalityBritish[2]EducationKing's College, TauntonAlma materUniversity of Cambridge (BA, PhD)Known forPulsarsSpouse Marjorie Richards (m. 1950)[3]Awards Hughes Medal (1977) Nobel Prize for Physics (1974) Eddington Medal (1969) Scientific careerFieldsRadio astronomyInstitu...

Filipino-Argentine singer (born 2002) ChantyChanty in 2023BornMaria Chantal Videla (2002-12-15) December 15, 2002 (age 20)Manila, PhilippinesOther namesChantal VidelaLee Hee-jinOccupationsSingeractressmodelAgentSparkleMusical careerOriginSouth KoreaGenresK-popYears active2017—presentLabelsMLDMember ofLapillus Musical artistKorean nameHangul이희진Hanja李姬振Revised RomanizationI Hee-jinMcCune–ReischauerYi Hŭichun Maria Chantal Videla[1] (Tagalog: [mɐˈɾija ʃ...

Ulrike Liedtke (2019) Ulrike Liedtke, geb. Nehrdich[1] (* 17. November 1958 in Weimar, DDR) ist eine deutsche Musikwissenschaftlerin und Politikerin (SPD). Von 1991 bis 2014 war sie Gründungsdirektorin der Musikakademie Rheinsberg. Seit 2014 ist sie Mitglied des Landtags Brandenburg. Nach der Wiederwahl 2019 wurde sie zur Landtagspräsidentin gewählt. Inhaltsverzeichnis 1 Leben 2 Politik 3 Mitgliedschaften 4 Ehrungen 5 Schriften (Auswahl) 6 Weblinks 7 Einzelnachweise Leben Ulrike Li...

Pour les articles homonymes, voir Georges Ier. Georges Ier RákócziGeorges Ier RákócziTitre de noblesseBaronBiographieNaissance 8 juin 1593SzerencsDécès 11 octobre 1648 (à 55 ans)Alba IuliaSépulture Cathédrale Saint-Michel d’Alba IuliaActivité ÉcrivainFamille Famille RákócziPère Sigismond II RákócziMère Anna Gerendi (d)Fratrie Erzsébet Rákóczi (d)Zsigmond Rákóczi (d)Pál Rákóczi (d)Conjoint Zsuzsanna LorántffyEnfants Georges II RákócziZsigmond R...

Discs of Sulguni cheese This is a list of Georgian cheeses. Over 250 varieties of cheese are produced in Georgia.[1] Georgian cheeses Tenili cheese Dambal khacho[2] Guda, cheese from eastern Georgia's mountain region[1][3] Imeruli,[3] cheese from Imereti region Kalti[2] Rotten cheese[2] Sulguni,[3] cheese from Samegrelo region. It is sometimes smoked.[1] Svanetian marchvi[2] Tenili cheese, a variety of string chee...

Motorway on the Gold Coast, Queensland, Australia Tugun BypassPacific MotorwayQueensland–New South WalesGeneral informationTypeFreewayLocationTugunLength7 km (4.3 mi)OpenedJuly 2008Route number(s)Major junctionsNE end Pacific Motorway Currumbin, Gold Coast SW end Pacific Motorway Tweed Heads, New South Wales Highway system Highways in Australia National Highway • Freeways in Australia Highways in Queensland Highways in New South Wales Main article: Pacific Motorway ...

You can help expand this article with text translated from the corresponding article in German. (March 2010) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedi...

Petirtaan kuno Jolotundo Petirtaan Jolotundo disebut juga dengan Candi Jolotundo atau Jalatunda adalah kompleks petirtaan kuno yang merupakan kawasan kolam suci petirtaan yang dibangun sejak masa Kerajaan Medang yang telah berpindah dari Jawa Tengah ke Jawa Timur, atau lazim disebut Medang periode Jawa Timur dan masih berfungsi hingga sekarang, dugaan paling awal diperkirakan dibangun pada masa pemerintahan Sri Isyana Tunggawijaya putri raja Medang (Mpu Sindok) dengan suaminya Sri Lokapala ya...

Ten artykuł dotyczy duchownego i oficera WP. Zobacz też: inne osoby o tym imieniu i nazwisku. Stanisław Julian Michalski Data i miejsce urodzenia 3 maja 1916 Stodoły Data i miejsce śmierci 25 września 2003 Rzym Wyznanie katolicyzm Kościół rzymskokatolicki Prezbiterat 20 grudnia 1952 Odznaczenia pułkownik Data urodzenia 3 maja 1916 Data śmierci 25 września 2003 Przebieg służby Lata służby 1938–1945 Siły zbrojne Wojsko Polskie Polskie Siły Zbro...

округРязанский округ Страна СССР Входил в Московская область Адм. центр Рязань История и география Дата образования 1929-1930 Дата упразднения 23 июля 1930 Рязанский округ — административно-территориальная единица Московской области, существовавшая в 1929—1930 годах. Ряза�...