Эффект Фарадея
|
Read other articles:

English brewer and politician For other uses, see Whitbread (disambiguation). Samuel WhitbreadParliamentary ProcedureWhitbread as caricatured by Spy (Leslie Ward) in Vanity Fair, August 1895Member of Parliamentfor BedfordIn office1852–1895Serving with Henry Stuart 1852–1854William Stuart 1854–1857 & 1859–1868Thomas Barnard 1857–1859James Howard 1868–1874Frederick Charles Polhill-Turner 1874–1880Charles Magniac 1880–1885Preceded byHenry StuartSir Harry Verney, BtSuc...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Joseba Sarrionandia Joseba Sarrionandia Uribelarrea (lahir 13 April 1958) adalah seorangpenulis Basque. Ia menulis banyak buku puisi, cerita pendek dan novel. Pada tahun 1985, ia lolos dari penjara setelah ditangkap sebagai anggota grup bersenjata Bas...

Stadium Australia, home of the NRL Grand Final Old Trafford, home of the Super League Grand Final The following is a list of stadiums at which rugby league is played, ordered by seating capacity. All stadiums with a capacity of 5,000 or more which are the regular home venue of a club or national team, or are the regular hosts of a major competition (such as the State of Origin series, Magic Weekend, or the final of an annual national competition), are included. Stadiums for which the only rug...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2021) تعرف نسبة ضغط البيانات أو قوة الضغط بمقاييس الانخفاض في حجم البيانات المماثلة التي تولد من ضغط البيانات الخوارزمية، ويعبر عنها غالبا تقسيم البيانات غير الم�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Jytte Laila Zabell Abildstrøm MygindLahir25 Maret 1934 (umur 89)Copenhagen, DenmarkPekerjaanPemeranTahun aktif1956-kini Jytte Abildstrøm (lahir 25 Maret 1934) adalah seorang pemeran film Denmark. Ia tampil dalam 40 film sejak 1956. Ia lahi...

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (beispielsweise Einzelnachweisen) ausgestattet. Angaben ohne ausreichenden Beleg könnten demnächst entfernt werden. Bitte hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Power Metal ist ein Metal-Subgenre hauptsächlich europäischen Ursprungs.[1] Vor der europäischen Strömung entstand auch ein US-amerikanischer Metal-Stil gleichen Namens, der jedoch nicht die Popularität de...

1st United Nations Deputy Secretary-General Louise FréchetteOCLouise Fréchette in May 20151st United Nations Deputy Secretary-GeneralIn office1 April 1997 – 1 April 2006Secretary-GeneralKofi AnnanPreceded byOffice establishedSucceeded byMark Malloch-BrownCanadian Ambassador to the United NationsIn officeJanuary 1992 – December 1994Preceded byYves FortierSucceeded byRobert Fowler Personal detailsBorn (1946-07-16) July 16, 1946 (age 77)MontrealNationalityCanadia...

«Лукас» Кременчук Повна назва Футбольний клуб «Лукас» (Кременчук) Прізвисько кондитери Засновано 2009 Розформовано 2015 Населений пункт Кременчук, Україна Стадіон СК «Політехнік» Вміщує 500[1] Президент Олександр Віталійович Порохня Головний тренер Валентин Цвелих Ліг�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 15th century – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this template message) Millennium 2nd millennium Centuries 14th century 15th century 16th century Timelines 14th century 15th ...

Sourcebook for GURPS game system GURPS HumanxCoverPublishersSteve Jackson GamesSystemsGURPS GURPS Humanx is a sourcebook for GURPS. Contents GURPS Humanx is a GURPS supplement of science-fiction role-playing rules set in an interstellar commonwealth of humans and the Thranx, allied insectoid aliens. The book covers character rules for nine alien races, basic psionics, spacecraft and equipment. The Commonwealth Gazetteer section describes the inhabited planets, their cultures, and hi...

2008 live album by Chayanne Chayanne: VivoLive album by ChayanneReleasedOctober 28, 2008RecordedLive in 2007 at the River Plate Stadium, Buenos Aires, ArgentinaGenreLatin popLength52:50Chayanne chronology Mi Tiempo(2007) Chayanne: Vivo(2008) De Piel A Piel(2008) Chayanne: Vivo is the first live album by Puerto Rican singer Chayanne. The earliest songs from this album are from Provócame (1992). Track listing Y Tú Te Vas Yo Te Amo (Atado a Tu Amor medley) No Te Preocupes Por Mi Caprichosa...

Bài viết này là một bài mồ côi vì không có bài viết khác liên kết đến nó. Vui lòng tạo liên kết đến bài này từ các bài viết liên quan; có thể thử dùng công cụ tìm liên kết. (tháng 7 2018) Hiệp hội Quốc tế về Tự do Cá nhânTên viết tắtISILThành lập1969LoạiTổ chức phi chính phủ, phi lợi nhuậnVùng phục vụ Toàn cầuNgôn ngữ chính Tiếng AnhTrang webISIL Official website Hiệp hội Quốc tế ...

Kartu Vaksin Covid-19 yang dikeluarkan oleh Kementerian Kesehatan Republik Indonesia. Kartu vaksin kosong yang dikeluarkan oleh Pusat Pengendalian dan Pencegahan Penyakit Amerika Serikat. Bagian dari seri artikel mengenaiPandemi Covid-19Permodelan atomik akurat yang menggambarkan struktur luar virus SARS-CoV-2. Tiap bola yang tergambarkan di sini adalah sebuah atom. SARS-CoV-2 (virus) Covid-19 (penyakit) Kronologi2019 2020 Januari Februari Maret April Mei Juni Juli Agustus September Oktober N...

Kyle Rote Jr. Nazionalità Stati Uniti Altezza 183 cm Calcio Ruolo Allenatore (ex attaccante) Termine carriera 1979 Carriera Giovanili 1969-1972 Sewanee Tigers1966-19?? Black Bandits Squadre di club1 1972-1978 Dallas Tornado121 (42)1979 Houston Hurricane21 (1) Nazionale 1973-1975 Stati Uniti5 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Indoor soccer Termine carriera 1...

6th-century Arab chieftain and poet For other uses, see Hatimtai. Hatim Al-Tayyi (left) depicted in an Urdu Diwan Hatim Tai redirects here. For the films, see Hatim Tai (1956 film) and Haatim Tai (1990 film). Hatim al-Tai (Arabic: حاتم الطائي, 'Hatim of the Tayy tribe'; died 578), full name Ḥātim bin ʿAbd Allāh bin Saʿd aṭ-Ṭāʾiyy (Arabic: حاتم بن عبد الله بن سعد الطائي) was an Arab chieftain of the Tayyi tribe of Arabia, ruler of Shammar, and poet...

Skema stasiun lisimeter;(a) tanah;(b) timbangan tanah;(c) penampung perkolasi;(d) penampung limpasan permukaan Stasiun lisimeter di Kittendorf, Germany Tangga menuju ruang inspeksi lisimeter di Kittendorf, Jerman Lisimeter adalah alat ukur yang digunakan untuk mengukur evapotranspirasi aktual yang dilepaskan oleh tumbuhan dan tanah di sekitarnya. Alat ini biasanya digunakan bersama dengan penakar curah hujan (pluviometer). Dengan mengetahui besar presipitasi dan perkolasi, evapotranspirasi da...

函館大谷短期大学 大学設置 1963年創立 1888年学校種別 私立設置者 学校法人函館大谷学園本部所在地 北海道函館市鍛治1-2-3北緯41度48分5.24秒 東経140度45分47.74秒 / 北緯41.8014556度 東経140.7632611度 / 41.8014556; 140.7632611座標: 北緯41度48分5.24秒 東経140度45分47.74秒 / 北緯41.8014556度 東経140.7632611度 / 41.8014556; 140.7632611学部 コミュニティー総合学科�...
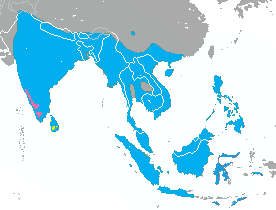
اضغط هنا للاطلاع على كيفية قراءة التصنيف زباد النخل المرتبة التصنيفية جنس[1][2] التصنيف العلمي فوق النطاق حيويات مملكة عليا خيطانيات مملكة نظائر حيوانات النحت عويلم كلوانيات مملكة فرعية ثانويات الفم شعبة شميات شعيبة فقاريات شعبة ف...

Jerry Orbach VidaNacimientu Nueva York[1], 20 d'ochobre de 1935[2]Nacionalidá Estaos XuníosLlingua materna inglésMuerte Nueva York[3], 28 d'avientu de 2004[4] (69 años)Sepultura Cementerio de la Iglesia de la Trinidad (es) Causa de la muerte cáncanu de próstataFamiliaCasáu con Elaine Cancilla Orbach (1979 – 2004)Fíos/es Chris OrbachTony Orbach EstudiosEstudios Universidá d'Illinois n'Urbana-Champaign Northwest...









