Шестиугольная призма — призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин[1].
До заточки многие карандаши имеют форму длинной шестиугольной призмы[2].
Полуправильный (или однородный) многогранник
Если все боковые грани одинаковые, шестиугольная призма является полуправильным многогранником, более обще, однородным многогранником и четвёртой призмой в бесконечном множестве призм, образованных прямоугольными боковыми сторонами и двумя правильными основаниями. Призму можно рассматривать как усечённый[англ.] шестигранный осоэдр, представленный символом Шлефли t{2,6}. С другой стороны, его можно рассматривать как прямое произведение правильного шестиугольника на отрезок, которое представляется как {6}×{}. Двойственным многогранником шестиугольной призмы является шестиугольная бипирамида[англ.].
Группой симметрии прямой шестиугольной призмы является D6h с порядком 24, а группой вращений является D6 с порядком 12.
Объём
Как и у большинства призм, объём правильной шестигранной призмы можно найти умножением площади основания (с длиной стороны 
) на высоту 
, что даёт формулу[3]:
Симметрия
Топология однородной шестиугольной призмы могут иметь геометрические вариации с низкой симметрией:
| Симметрия
|
D6h, [2,6], (*622)
|
C6v, [6], (*66)
|
D3h, [2,3], (*322)
|
D3d, [2+,6], (2*3)
|
| Конструкция
|
{6}×{},    
|
|
t{3}×{}, 
|
|
s2{2,6},  
|
| Рисунок
|
![]()
|
|
|
|
|
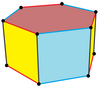
| Нарушение
|
|
|
|
|
|
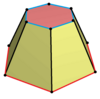
Как часть пространственных мозаик
Шестигранная призма присутствует как ячейка в четырёх призматических однородных выпуклых сотах[англ.] в трёхмерном пространстве:
Шестигранные призмы существуют также в качестве трёхмерных граней четырёхмерных однородных многогранников[англ.]:
Связанные многогранники и мозаики
Однородные шестиугольные диэдральные сферические многогранники
| Симметрия: [6,2], (*622)
|
[6,2]+, (622)
|
[6,2+], (2*3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| {6,2}
|
t{6,2}
|
r{6,2}
|
t{2,6}
|
{2,6}
|
rr{2,6}
|
tr{6,2}[англ.]
|
sr{6,2}
|
s{2,6}
|
| Двойственные им многогранники
|
|
|
|
|
|
|
|
|
|
|
| V62
|
V122
|
V62
|
V4.4.6[англ.]
|
V26
|
V4.4.6[англ.]
|
V4.4.12
|
V3.3.3.6[англ.]
|
V3.3.3.3
|
Этот многогранник можно считать членом последовательности однородных многогранников с угловой фигурой (4.6.2p) и диаграммой Коксетера — Дынкина 
. Для p < 6 членами последовательности являются усечённые во всех углах многогранники (зоноэдры), и они показаны ниже как сферические мозаики. Для p > 6 они являются мозаиками гиперболической плоскости начиная с усечённой трисемиугольной мозаики[англ.].
*n32 мутации по симметрии полностью усечённых мозаик: 4.6.2n
Симметрия
*n32[англ.]
n,3[англ.]
|
Сферическая
|
Евклидова
|
Компактная гиперболическая
|
Паракомп.
|
Некомпактная гиперболическая
|
*232
[2,3]
|
*332
[3,3]
|
*432
[4,3]
|
*532
[5,3]
|
*632
[6,3]
|
*732
[7,3]
|
*832
[8,3]
|
*∞32
[∞,3]
|
[12i,3]
|
[9i,3]
|
[6i,3]
|
[3i,3]
|
| Фигуры
|
|
|
|
|
|
|
|
|
|
|
|
|
| Конфигурация
|
4.6.4
|
4.6.6
|
4.6.8
|
4.6.10
|
4.6.12[англ.]
|
4.6.14[англ.]
|
4.6.16[англ.]
|
4.6.∞[англ.]
|
4.6.24i
|
4.6.18i
|
4.6.12i
|
4.6.6i
|
| Двойственная
|
|
|
|
|
|
|
|
|
|
|
|
|
| Конфигурация грани
|
V4.6.4[англ.]
|
V4.6.6
|
V4.6.8[англ.]
|
V4.6.10
|
V4.6.12[англ.]
|
V4.6.14[англ.]
|
V4.6.16[англ.]
|
V4.6.∞
|
V4.6.24i
|
V4.6.18i
|
V4.6.12i
|
V4.6.6i
|
См. также
Примечания
Ссылки
