ذںر€ر‹ذ³ذ°رژر‰ذ¸ذ¹ ذ¼رڈر‡. ذ”ذ²ذ¸ذ¶ذµذ½ذ¸ذµ ذ½ذµ رپذ¾ذ²رپذµذ¼ ذ؟ذ°ر€ذ°ذ±ذ¾ذ»ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ¸ذ·-ذ·ذ° رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ ذ²ذ¾ذ·ذ´رƒر…ذ° . ذ¤ذ¸ذ·ذ¸ذ؛ذ° ذ؟ر€ر‹ذ³ذ°رژر‰ذµذ³ذ¾ ذ¼رڈر‡ذ° ذ؛ذ°رپذ°ذµر‚رپرڈ ر„ذ¸ذ·ذ¸ر‡ذµرپذ؛ذ¾ذ³ذ¾ ذ؟ذ¾ذ²ذµذ´ذµذ½ذ¸رڈ ذ؟ر€ر‹ذ³ذ°رژر‰ذµذ³ذ¾ ذ¼رڈر‡ذ° , ذ² ر‡ذ°رپر‚ذ½ذ¾رپر‚ذ¸ ذµذ³ذ¾ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ ذ´ذ¾, ذ²ذ¾ ذ²ر€ذµذ¼رڈ ذ¸ ذ؟ذ¾رپذ»ذµ رƒذ´ذ°ر€ذ° ذ¾ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ ذ´ر€رƒذ³ذ¾ذ³ذ¾ ر‚ذµذ»ذ° . ذذµذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ°رپذ؟ذµذ؛ر‚ر‹ ذ؟ذ¾ذ²ذµذ´ذµذ½ذ¸رڈ ذ؟ر€ر‹ذ³ذ°رژر‰ذµذ³ذ¾ ذ¼رڈر‡ذ° رپذ»رƒذ¶ذ°ر‚ ذ²ذ²ذµذ´ذµذ½ذ¸ذµذ¼ ذ² ذ¼ذµر…ذ°ذ½ذ¸ذ؛رƒ ذ½ذ° ذ؛رƒر€رپذ°ر… ر„ذ¸ذ·ذ¸ذ؛ذ¸ ذ² رپر€ذµذ´ذ½ذµذ¹ رˆذ؛ذ¾ذ»ذµ ذ¸ذ»ذ¸ ذ±ذ°ذ؛ذ°ذ»ذ°ذ²ر€ذ¸ذ°ر‚ذµ . ذذ´ذ½ذ°ذ؛ذ¾ ر‚ذ¾ر‡ذ½ذ¾ذµ ذ¼ذ¾ذ´ذµذ»ذ¸ر€ذ¾ذ²ذ°ذ½ذ¸ذµ ذ؟ذ¾ذ²ذµذ´ذµذ½ذ¸رڈ رپذ»ذ¾ذ¶ذ½ذ¾ ذ¸ ذ؟ر€ذµذ´رپر‚ذ°ذ²ذ»رڈذµر‚ ذ¸ذ½ر‚ذµر€ذµرپ ذ´ذ»رڈ رپذ؟ذ¾ر€ر‚ذ¸ذ²ذ½ذ¾ذ¹ ذ¸ذ½ذ¶ذµذ½ذµر€ذ¸ذ¸ .
ذ”ذ²ذ¸ذ¶ذµذ½ذ¸ذµ ذ¼رڈر‡ذ° ذ¾ذ±ر‹ر‡ذ½ذ¾ ذ¾ذ؟ذ¸رپر‹ذ²ذ°ذµر‚رپرڈ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸ذµذ¼ رپذ½ذ°ر€رڈذ´ذ° (ذ½ذ° ذ؛ذ¾ر‚ذ¾ر€ذ¾ذµ ذ¼ذ¾ذ³رƒر‚ ذ²ذ»ذ¸رڈر‚رŒ ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸رڈ , رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸ذµ , رچر„ر„ذµذ؛ر‚ ذœذ°ذ³ذ½رƒرپذ° ذ¸ ذ؟ذ»ذ°ذ²رƒر‡ذµرپر‚رŒ ), ر‚ذ¾ذ³ذ´ذ° ذ؛ذ°ذ؛ ذµذ³ذ¾ ذ²ذ¾ذ·ذ´ذµذ¹رپر‚ذ²ذ¸ذµ ذ¾ذ±ر‹ر‡ذ½ذ¾ ر…ذ°ر€ذ°ذ؛ر‚ذµر€ذ¸ذ·رƒذµر‚رپرڈ ذ؛ذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ذ¾ذ¼ ذ²ذ¾رپرپر‚ذ°ذ½ذ¾ذ²ذ»ذµذ½ذ¸رڈ (ذ½ذ° ذ؛ذ¾ر‚ذ¾ر€ر‹ذ¹ ذ¼ذ¾ذ¶ذµر‚ ذ²ذ»ذ¸رڈر‚رŒ ذ؟ر€ذ¸ر€ذ¾ذ´ذ° رˆذ°ر€ذ°, ر…ذ°ر€ذ°ذ؛ر‚ذµر€ رƒذ´ذ°ر€رڈرژر‰ذµذ¹ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸, رپذ؛ذ¾ر€ذ¾رپر‚رŒ رƒذ´ذ°ر€ذ°, ذ²ر€ذ°ر‰ذµذ½ذ¸ذµ ذ¸ ذ¼ذµرپر‚ذ½ر‹ذµ رƒرپذ»ذ¾ذ²ذ¸رڈ, ر‚ذ°ذ؛ذ¸ذµ ذ؛ذ°ذ؛ ر‚ذµذ¼ذ؟ذµر€ذ°ر‚رƒر€ذ° ذ¸ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ). ذ§ر‚ذ¾ذ±ر‹ ذ¾ذ±ذµرپذ؟ذµر‡ذ¸ر‚رŒ ر‡ذµرپر‚ذ½رƒرژ ذ¸ذ³ر€رƒ , ذ¼ذ½ذ¾ذ³ذ¸ذµ رپذ؟ذ¾ر€ر‚ذ¸ذ²ذ½ر‹ذµ ر€رƒذ؛ذ¾ذ²ذ¾ذ´رڈر‰ذ¸ذµ ذ¾ر€ذ³ذ°ذ½ر‹ رƒرپر‚ذ°ذ½ذ°ذ²ذ»ذ¸ذ²ذ°رژر‚ ذ¾ذ³ر€ذ°ذ½ذ¸ر‡ذµذ½ذ¸رڈ ذ½ذ° رƒذ؟ر€رƒذ³ذ¾رپر‚رŒ ذ¼رڈر‡ذ° ذ¸ ذ·ذ°ذ؟ر€ذµر‰ذ°رژر‚ ذ¸ذ·ذ¼ذµذ½ذµذ½ذ¸ذµ ذµذ³ذ¾ ذ°رچر€ذ¾ذ´ذ¸ذ½ذ°ذ¼ذ¸ر‡ذµرپذ؛ذ¸ر… رپذ²ذ¾ذ¹رپر‚ذ². ذر‚رپذ؛ذ¾ذ؛ ذ¼رڈر‡ذµذ¹ ذ±ر‹ذ» ر…ذ°ر€ذ°ذ؛ر‚ذµر€ذ½ذ¾ذ¹ ر‡ذµر€ر‚ذ¾ذ¹ ر‚ذ°ذ؛ذ¸ر… ذ´ر€ذµذ²ذ½ذ¸ر… ذ²ذ¸ذ´ذ¾ذ² رپذ؟ذ¾ر€ر‚ذ°, ذ؛ذ°ذ؛ ذ¼ذµذ·ر€ذ°ذ¼ذµر€ذ¸ذ؛ذ°ذ½رپذ؛ذ°رڈ ذ¸ذ³ر€ذ° ذ² ذ¼رڈر‡ [ 1]
ذ،ذ¸ذ»ر‹, ذ´ذµذ¹رپر‚ذ²رƒرژر‰ذ¸ذµ ذ½ذ° ذ²ر€ذ°ر‰ذ°رژر‰ذ¸ذ¹رپرڈ رˆذ°ر€ ذ²ذ¾ ذ²ر€ذµذ¼رڈ ذµذ³ذ¾ ذ؟ذ¾ذ»ر‘ر‚ذ°, — رچر‚ذ¾ رپذ¸ذ»ذ° ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸ذ¸ (FG ), رپذ¸ذ»ذ° رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ ذ²ذ¾ذ·ذ´رƒر…ذ° (FD ), رپذ¸ذ»ذ° ذœذ°ذ³ذ½رƒرپذ° (FM ) ذ¸ ذ؟ذ»ذ°ذ²رƒر‡ذµرپر‚رŒ (FB ). ذ”ذ²ذ¸ذ¶ذµذ½ذ¸ذµ ذ؟ر€ر‹ذ³ذ°رژر‰ذµذ³ذ¾ ذ¼رڈر‡ذ° ذ°ذ½ذ°ذ»ذ¾ذ³ذ¸ر‡ذ½ذ¾ ذ؟ذ¾ذ»ر‘ر‚رƒ رپذ½ذ°ر€رڈذ´ذ° [ 2] [ 3] رپذ¸ذ»ذ° ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸ذ¸ (F G ), ذ»ذ¾ذ±ذ¾ذ²ذ¾ذµ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸ذµ ذ¸ذ·-ذ·ذ° رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ ذ²ذ¾ذ·ذ´رƒر…ذ° (F D ), رپذ¸ذ»ذ° ذœذ°ذ³ذ½رƒرپذ° ذ¸ذ·-ذ·ذ° ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° (F M ) ذ¸ رپذ¸ذ»ذ° ذ؟ذ»ذ°ذ²رƒر‡ذµرپر‚ذ¸ (F B ). ذ’ ذ¾ذ±ر‰ذµذ¼ رپذ»رƒر‡ذ°ذµ ذ´ذ»رڈ ذ°ذ½ذ°ذ»ذ¸ذ·ذ° ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° ذ½ذµذ¾ذ±ر…ذ¾ذ´ذ¸ذ¼ذ¾ ذ¸رپذ؟ذ¾ذ»رŒذ·ذ¾ذ²ذ°ر‚رŒ ذ²ر‚ذ¾ر€ذ¾ذ¹ ذ·ذ°ذ؛ذ¾ذ½ ذرŒرژر‚ذ¾ذ½ذ° رپ رƒر‡ر‘ر‚ذ¾ذ¼ ذ²رپذµر… رپذ¸ذ»:
∑ ∑ -->
F
=
m
a
,
F
G
+
F
D
+
F
M
+
F
B
=
m
a
=
m
d
v
d
t
=
m
d
2
r
d
t
2
,
{\displaystyle {\begin{aligned}\sum \mathbf {F} &=m\mathbf {a} ,\\\mathbf {F} _{\text{G}}+\mathbf {F} _{\text{D}}+\mathbf {F} _{\text{M}}+\mathbf {F} _{\text{B}}&=m\mathbf {a} =m{\frac {d\mathbf {v} }{dt}}=m{\frac {d^{2}\mathbf {r} }{dt^{2}}},\end{aligned}}}
ذ³ذ´ذµ m — ذ¼ذ°رپرپذ° ذ¼رڈر‡ذ°. ذ—ذ´ذµرپرŒ ذ²ذµذ؛ر‚ذ¾ر€ذ° a , v , r ذ¾ذ±ذ¾ذ·ذ½ذ°ر‡ذ°رژر‚ رƒرپذ؛ذ¾ر€ذµذ½ذ¸ذµ , رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¸ ذ؟ذ¾ذ»ذ¾ذ¶ذµذ½ذ¸ذµ ذ¼رڈر‡ذ° ذ² ذ¼ذ¾ذ¼ذµذ½ر‚ ذ²ر€ذµذ¼ذµذ½ذ¸ t .
ذ¢ر€ذ°ذµذ؛ر‚ذ¾ر€ذ¸رڈ ذ¼رڈر‡ذ°, ذ¾ر‚رپذ؛ذ°ذ؛ذ¸ذ²ذ°رژر‰ذµذ³ذ¾ ذ؟ذ¾ذ´ رƒذ³ذ»ذ¾ذ¼ 70آ° ذ؟ذ¾رپذ»ذµ رƒذ´ذ°ر€ذ°. ذ§ر‘ر€ذ½ر‹ذ¹ ذ¾ذ±رٹذµذ؛ر‚ ذ½ذµ ذ¸رپذ؟ر‹ر‚ر‹ذ²ذ°ذµر‚ ذ½ذ¸ذ؛ذ°ذ؛ذ¾ذ³ذ¾ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ ذ¸ ذ´ذ²ذ¸ذ¶ذµر‚رپرڈ ذ؟ذ¾ ذ؟ذ°ر€ذ°ذ±ذ¾ذ»ذµ, ذ½ذ° ذ³ذ¾ذ»رƒذ±ذ¾ذ¹ ذ¾ذ±رٹذµذ؛ر‚ ذ´ذµذ¹رپر‚ذ²رƒذµر‚ ذ·ذ°ذ؛ذ¾ذ½ ذ،ر‚ذ¾ذ؛رپذ° , ذ½ذ° ذ·ذµذ»ر‘ذ½ر‹ذ¹ ذ¾ذ±رٹذµذ؛ر‚ — ذ·ذ°ذ؛ذ¾ذ½ ذ²رڈذ·ذ؛ذ¾رپر‚ذ¸ ذرŒرژر‚ذ¾ذ½ذ° . ذ،ذ¸ذ»ذ° ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸ذ¸ ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ° ذ²ذ½ذ¸ذ· ذ¸ ر€ذ°ذ²ذ½ذ°[ 4]
F
G
=
m
g
,
{\displaystyle F_{\text{G}}=mg,}
ذ³ذ´ذµ m — ذ¼ذ°رپرپذ° ذ¼رڈر‡ذ°, ذ° g — رƒرپذ؛ذ¾ر€ذµذ½ذ¸ذµ رپذ²ذ¾ذ±ذ¾ذ´ذ½ذ¾ذ³ذ¾ ذ؟ذ°ذ´ذµذ½ذ¸رڈ , ذ؛ذ¾ر‚ذ¾ر€ذ¾ذµ ذ½ذ° ذ—ذµذ¼ذ»ذµ ذ؛ذ¾ذ»ذµذ±ذ»ذµر‚رپرڈ ذ² ذ؟ر€ذµذ´ذµذ»ذ°ر… 9,764 ذ¸ 9,834 ذ¼/رپ2 [ 5] ذ¸ذ´ذµذ°ذ»ذ¸ذ·ذ¸ر€رƒذµر‚رپرڈ ذ؛ذ°ذ؛ ذ؟ر€ذ¾ذ¸رپر…ذ¾ذ´رڈر‰ذµذµ ر‚ذ¾ذ»رŒذ؛ذ¾ ذ؟ذ¾ذ´ ذ´ذµذ¹رپر‚ذ²ذ¸ذµذ¼ رپذ¸ذ»ر‹ ر‚رڈذ¶ذµرپر‚ذ¸. ذ•رپذ»ذ¸ ذ½ذ° ذ¼رڈر‡ ذ´ذµذ¹رپر‚ذ²رƒذµر‚ ر‚ذ¾ذ»رŒذ؛ذ¾ رپذ¸ذ»ذ° ر‚رڈذ¶ذµرپر‚ذ¸, ر‚ذ¾ ذ¼ذµر…ذ°ذ½ذ¸ر‡ذµرپذ؛ذ°رڈ رچذ½ذµر€ذ³ذ¸رڈ رپذ¾ر…ر€ذ°ذ½ذ¸ر‚رپرڈ ذ²ذ¾ ذ²ر€ذµذ¼رڈ ذµذ³ذ¾ ذ؟ذ¾ذ»ر‘ر‚ذ°. ذ’ رچر‚ذ¾ذ¼ ذ¸ذ´ذµذ°ذ»ذ¸ذ·ذ¸ر€ذ¾ذ²ذ°ذ½ذ½ذ¾ذ¼ رپذ»رƒر‡ذ°ذµ رƒر€ذ°ذ²ذ½ذµذ½ذ¸رڈ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ ذ¸ذ¼ذµرژر‚ ذ²ذ¸ذ´
a
=
− − -->
g
j
^ ^ -->
,
v
=
v
0
+
a
t
,
r
=
r
0
+
v
0
t
+
1
2
a
t
2
,
{\displaystyle {\begin{aligned}\mathbf {a} &=-g\mathbf {\hat {j}} ,\\\mathbf {v} &=\mathbf {v} _{\text{0}}+\mathbf {a} t,\\\mathbf {r} &=\mathbf {r} _{0}+\mathbf {v} _{0}t+{\frac {1}{2}}\mathbf {a} t^{2},\end{aligned}}}
ذ³ذ´ذµ a , v ذ¸ r — رƒرپذ؛ذ¾ر€ذµذ½ذ¸ذµ, رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¸ ذ؟ذ¾ذ»ذ¾ذ¶ذµذ½ذ¸ذµ ذ¼رڈر‡ذ°, ذ° v 0 ذ¸ r 0 — ذ½ذ°ر‡ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¸ ذ؟ذ¾ذ»ذ¾ذ¶ذµذ½ذ¸ذµ ذ¼رڈر‡ذ° رپذ¾ذ¾ر‚ذ²ذµر‚رپر‚ذ²ذµذ½ذ½ذ¾.
ذ’ ذ؛ذ¾ذ¾ر€ذ´ذ¸ذ½ذ°ر‚ذ½ذ¾ذ¹ ذ·ذ°ذ؟ذ¸رپذ¸, ذµرپذ»ذ¸ ذ¼رڈر‡ ذ¾ر‚رپذ؛ذ°ذ؛ذ¸ذ²ذ°ذµر‚ ذ؟ذ¾ذ´ رƒذ³ذ»ذ¾ذ¼ خ¸ ذ؛ ذ·ذµذ¼ذ»ذµ, ذ´ذ²ذ¸ذ¶ذµذ½ذ¸ذµ ذ؟ذ¾ ذ¾رپرڈذ¼ x ذ¸ y (ذ؟ر€ذµذ´رپر‚ذ°ذ²ذ»رڈرژر‰ذµذµ ذ³ذ¾ر€ذ¸ذ·ذ¾ذ½ر‚ذ°ذ»رŒذ½ذ¾ذµ ذ¸ ذ²ذµر€ر‚ذ¸ذ؛ذ°ذ»رŒذ½ذ¾ذµ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸ذµ رپذ¾ذ¾ر‚ذ²ذµر‚رپر‚ذ²ذµذ½ذ½ذ¾) ذ¾ذ؟ذ¸رپر‹ذ²ذ°ذµر‚رپرڈ ر„ذ¾ر€ذ¼رƒذ»ذ¾ذ¹[ 6]
ذ¾رپرŒ X
ذ¾رپرŒ Y
a
x
=
0
,
v
x
=
v
0
cos
âپ، -->
(
θ خ¸ -->
)
,
x
=
x
0
+
v
0
cos
âپ، -->
(
θ خ¸ -->
)
t
,
{\displaystyle {\begin{aligned}a_{\text{x}}&=0,\\v_{\text{x}}&=v_{0}\cos \left(\theta \right),\\x&=x_{0}+v_{0}\cos \left(\theta \right)t,\end{aligned}}}
a
y
=
− − -->
g
,
v
y
=
v
0
sin
âپ، -->
(
θ خ¸ -->
)
− − -->
g
t
,
y
=
y
0
+
v
0
sin
âپ، -->
(
θ خ¸ -->
)
t
− − -->
1
2
g
t
2
.
{\displaystyle {\begin{aligned}a_{\text{y}}&=-g,\\v_{\text{y}}&=v_{0}\sin \left(\theta \right)-gt,\\y&=y_{0}+v_{0}\sin \left(\theta \right)t-{\frac {1}{2}}gt^{2}.\end{aligned}}}
ذکذ· رƒر€ذ°ذ²ذ½ذµذ½ذ¸ذ¹ رپذ»ذµذ´رƒذµر‚, ر‡ر‚ذ¾ ذ¼ذ°ذ؛رپذ¸ذ¼ذ°ذ»رŒذ½ذ°رڈ ذ²ر‹رپذ¾ر‚ذ° (H ), ذ´ذ°ذ»رŒذ½ذ¾رپر‚رŒ (R ) ذ¸ ذ²ر€ذµذ¼رڈ ذ؟ذ¾ذ»ر‘ر‚ذ° (T ) ذ¼رڈر‡ذ°, ذ¾ر‚رپذ؛ذ°ذ؛ذ¸ذ²ذ°رژر‰ذµذ³ذ¾ ذ¾ر‚ ذ؟ذ»ذ¾رپذ؛ذ¾ذ¹ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸, ذ¾ذ؟ر€ذµذ´ذµذ»رڈرژر‚رپرڈ ذ²ر‹ر€ذ°ذ¶ذµذ½ذ¸رڈذ¼ذ¸[ 2] [ 6]
H
=
v
0
2
2
g
sin
2
âپ، -->
(
θ خ¸ -->
)
,
R
=
v
0
2
g
sin
âپ، -->
(
2
θ خ¸ -->
)
,
and
T
=
2
v
0
g
sin
âپ، -->
(
θ خ¸ -->
)
.
{\displaystyle {\begin{aligned}H&={\frac {v_{0}^{2}}{2g}}\sin ^{2}\left(\theta \right),\\R&={\frac {v_{0}^{2}}{g}}\sin \left(2\theta \right),~{\text{and}}\\T&={\frac {2v_{0}}{g}}\sin \left(\theta \right).\end{aligned}}}
ذ”ذ°ذ»رŒذ½ذµذ¹رˆذ¸ذµ رƒر‚ذ¾ر‡ذ½ذµذ½ذ¸رڈ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° ذ¼ذ¾ذ¶ذ½ذ¾ ذ²ذ½ذµرپر‚ذ¸, ذ؟ر€ذ¸ذ½رڈذ² ذ²ذ¾ ذ²ذ½ذ¸ذ¼ذ°ذ½ذ¸ذµ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸ذµ ذ²ذ¾ذ·ذ´رƒر…ذ° (ذ¸ رپذ²رڈذ·ذ°ذ½ذ½ر‹ذµ رپ ذ½ذ¸ذ¼ رچر„ر„ذµذ؛ر‚ر‹, ر‚ذ°ذ؛ذ¸ذµ ذ؛ذ°ذ؛ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸ذµ ذ¸ ذ²ذµر‚ذµر€ ), رچر„ر„ذµذ؛ر‚ ذœذ°ذ³ذ½رƒرپذ° ذ¸ ذ؟ذ»ذ°ذ²رƒر‡ذµرپر‚رŒ . ذںذ¾رپذ؛ذ¾ذ»رŒذ؛رƒ ذ±ذ¾ذ»ذµذµ ذ»ر‘ذ³ذ؛ذ¸ذµ ذ¼رڈر‡ذ¸ رƒرپذ؛ذ¾ر€رڈرژر‚رپرڈ ذ±ر‹رپر‚ر€ذµذµ, ر‚ذ¾ رچر‚ذ¸ رپذ¸ذ»ر‹ ذ¾ذ؛ذ°ذ·ر‹ذ²ذ°رژر‚ ذ±ذ¾ذ»رŒرˆذµذµ ذ²ذ»ذ¸رڈذ½ذ¸ذµ ذ½ذ° ذ¸ر… ذ´ذ²ذ¸ذ¶ذµذ½ذ¸ذµ.
ذذ±ر‚ذµذ؛ذ°ذ½ذ¸ذµ رˆذ°ر€ذ° ذ²ذ¾ذ·ذ´رƒر…ذ¾ذ¼ ذ¼ذ¾ذ¶ذµر‚ ذ±ر‹ر‚رŒ ذ؛ذ°ذ؛ ذ»ذ°ذ¼ذ¸ذ½ذ°ر€ذ½ر‹ذ¼ , ر‚ذ°ذ؛ ذ¸ ر‚رƒر€ذ±رƒذ»ذµذ½ر‚ذ½ر‹ذ¼ ذ² ذ·ذ°ذ²ذ¸رپذ¸ذ¼ذ¾رپر‚ذ¸ ذ¾ر‚ ر‡ذ¸رپذ»ذ° ذ ذµذ¹ذ½ذ¾ذ»رŒذ´رپذ° (Re), ذ¾ذ؟ر€ذµذ´ذµذ»رڈذµذ¼ذ¾ذ³ذ¾ ذ؛ذ°ذ؛:
Re
=
ρ دپ -->
D
v
μ خ¼ -->
,
{\displaystyle {\text{Re}}={\frac {\rho Dv}{\mu }},}
ذ³ذ´ذµ دپ — ذ؟ذ»ذ¾ر‚ذ½ذ¾رپر‚رŒ ذ²ذ¾ذ·ذ´رƒر…ذ° , خ¼ — ذ´ذ¸ذ½ذ°ذ¼ذ¸ر‡ذµرپذ؛ذ°رڈ ذ²رڈذ·ذ؛ذ¾رپر‚رŒ ذ²ذ¾ذ·ذ´رƒر…ذ°, D — ذ´ذ¸ذ°ذ¼ذµر‚ر€ ذ¼رڈر‡ذ°, ذ° v — رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¼رڈر‡ذ° ذ² ذ²ذ¾ذ·ذ´رƒر…ذµ. ذںر€ذ¸ ر‚ذµذ¼ذ؟ذµر€ذ°ر‚رƒر€ذµ 20 degC , ρ = 1,2 ذ؛ذ³/ذ¼3 μ = 1,8â‹…10−5 ذںذ°آ·رپ [ 7]
ذ•رپذ»ذ¸ ر‡ذ¸رپذ»ذ¾ ذ ذµذ¹ذ½ذ¾ذ»رŒذ´رپذ° ذ¾ر‡ذµذ½رŒ ذ¼ذ°ذ»ذ¾ (Re < 1), ذ¸ رپذ¸ذ»ذ° رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رژ ذ¼رڈر‡ذ° ذ¾ذ؟ذ¸رپر‹ذ²ذ°ذµر‚رپرڈ ذ·ذ°ذ؛ذ¾ذ½ذ¾ذ¼ ذ،ر‚ذ¾ذ؛رپذ° [ 8]
F
D
=
6
π د€ -->
μ خ¼ -->
r
v
,
{\displaystyle F_{\text{D}}=6\pi \mu rv,}
ذ³ذ´ذµ r — ر€ذ°ذ´ذ¸رƒرپ رˆذ°ر€ذ°. ذر‚ذ° رپذ¸ذ»ذ° ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ° ذ؟ر€ذ¾ر‚ذ¸ذ² ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° (ذ² ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸
− − -->
v
^ ^ -->
{\displaystyle \textstyle -{\hat {\mathbf {v} }}}
4 ذ´ذ¾ 105 , ذ¸ ذ·ذ°ذ؛ذ¾ذ½ ذ،ر‚ذ¾ذ؛رپذ° ذ½ذµذ؟ر€ذ¸ذ¼ذµذ½ذ¸ذ¼[ 9] ر„ذ¾ر€ذ¼رƒذ»ذ¾ذ¹ ذ»ذ¾ذ±ذ¾ذ²ذ¾ذ³ذ¾ ذ°رچر€ذ¾ذ´ذ¸ذ½ذ°ذ¼ذ¸ر‡ذµرپذ؛ذ¾ذ³ذ¾ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ [ 10]
F
D
=
1
2
ρ دپ -->
C
d
A
v
2
,
{\displaystyle F_{\text{D}}={\frac {1}{2}}\rho C_{\text{d}}Av^{2},}
ذ³ذ´ذµ C d — ذ؛ذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸رڈ ر„ذ¾ر€ذ¼ر‹ , ذ° A — ذ؟ذ»ذ¾ر‰ذ°ذ´رŒ ذ؟ذ¾ذ؟ذµر€ذµر‡ذ½ذ¾ذ³ذ¾ رپذµر‡ذµذ½ذ¸رڈ ذ¼رڈر‡ذ°.
ذ،ذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸ذµ ذ؟ر€ذ¸ذ²ذµذ´ر‘ر‚ ذ؛ ر‚ذ¾ذ¼رƒ, ر‡ر‚ذ¾ ذ¼رڈر‡ ذ؟ذ¾ر‚ذµر€رڈذµر‚ ذ¼ذµر…ذ°ذ½ذ¸ر‡ذµرپذ؛رƒرژ رچذ½ذµر€ذ³ذ¸رژ ذ²ذ¾ ذ²ر€ذµذ¼رڈ ذ؟ذ¾ذ»ر‘ر‚ذ°, ذ° ر‚ذ°ذ؛ذ¶ذµ رƒذ¼ذµذ½رŒرˆذ¸ر‚ ذµذ³ذ¾ ذ´ذ°ذ»رŒذ½ذ¾رپر‚رŒ ذ¸ ذ²ر‹رپذ¾ر‚رƒ, ذ° ذ±ذ¾ذ؛ذ¾ذ²ذ¾ذ¹ ذ²ذµر‚ذµر€ ذ¾ر‚ذ؛ذ»ذ¾ذ½ذ¸ر‚ ذµذ³ذ¾ ذ¾ر‚ ذ؟ذµر€ذ²ذ¾ذ½ذ°ر‡ذ°ذ»رŒذ½ذ¾ذ³ذ¾ ذ؟رƒر‚ذ¸. ذذ±ذ° رچر„ر„ذµذ؛ر‚ذ° ذ´ذ¾ذ»ذ¶ذ½ر‹ رƒر‡ذ¸ر‚ر‹ذ²ذ°ر‚رŒرپرڈ ذ¸ذ³ر€ذ¾ذ؛ذ°ذ¼ذ¸ ذ² ر‚ذ°ذ؛ذ¸ر… ذ²ذ¸ذ´ذ°ر… رپذ؟ذ¾ر€ر‚ذ°, ذ؛ذ°ذ؛ ذ³ذ¾ذ»رŒر„.
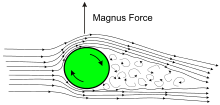
ذ،ذ¸ذ»ذ° ذœذ°ذ³ذ½رƒرپذ°, ذ´ذµذ¹رپر‚ذ²رƒرژر‰ذ°رڈ ذ½ذ° ذ¼رڈر‡ ذ؟ر€ذ¸ ذ¾ذ±ر€ذ°ر‚ذ½ذ¾ذ¼ ذ²ر€ذ°ر‰ذµذ½ذ¸ذ¸ . ذ—ذ°ذ؛ر€رƒر‡ذµذ½ذ½ر‹ذµ ذ»ذ¸ذ½ذ¸ذ¸ ذ؟ذ¾ر‚ذ¾ذ؛ذ° ذ؟ر€ذµذ´رپر‚ذ°ذ²ذ»رڈرژر‚ رپذ¾ذ±ذ¾ذ¹ ر‚رƒر€ذ±رƒذ»ذµذ½ر‚ذ½ر‹ذ¹ رپذ»ذµذ´ . ذ’ذ¾ذ·ذ´رƒرˆذ½ر‹ذ¹ ذ؟ذ¾ر‚ذ¾ذ؛ ذ¾ر‚ذ؛ذ»ذ¾ذ½رڈذµر‚رپرڈ ذ² رپر‚ذ¾ر€ذ¾ذ½رƒ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ. ذ’ر€ذ°ر‰ذµذ½ذ¸ذµ ذ¼رڈر‡ذ° ذ²ذ»ذ¸رڈذµر‚ ذ½ذ° ذµذ³ذ¾ ر‚ر€ذ°ذµذ؛ر‚ذ¾ر€ذ¸رژ ذ؟ذ¾رپر€ذµذ´رپر‚ذ²ذ¾ذ¼ رچر„ر„ذµذ؛ر‚ذ° ذœذ°ذ³ذ½رƒرپذ° . ذ،ذ¾ذ³ذ»ذ°رپذ½ذ¾ ر‚ذµذ¾ر€ذµذ¼ذµ ذڑرƒر‚ر‚ر‹ — ذ–رƒذ؛ذ¾ذ²رپذ؛ذ¾ذ³ذ¾ , ذ´ذ»رڈ ذ²ر€ذ°ر‰ذ°رژر‰ذµذ¹رپرڈ رپر„ذµر€ر‹ رپ ذ½ذµذ²رڈذ·ذ؛ذ¸ذ¼ ذ؟ذ¾ر‚ذ¾ذ؛ذ¾ذ¼ ذ²ذ¾ذ·ذ´رƒر…ذ° رپذ¸ذ»ذ° ذœذ°ذ³ذ½رƒرپذ° ر€ذ°ذ²ذ½ذ°[ 11]
F
M
=
8
3
π د€ -->
r
3
ρ دپ -->
ω د‰ -->
v
,
{\displaystyle F_{\text{M}}={\frac {8}{3}}\pi r^{3}\rho \omega v,}
ذ³ذ´ذµ r — ر€ذ°ذ´ذ¸رƒرپ رˆذ°ر€ذ°, د‰ — رƒذ³ذ»ذ¾ذ²ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ (ذ¸ذ»ذ¸ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ) ذ¼رڈر‡ذ°, دپ — ذ؟ذ»ذ¾ر‚ذ½ذ¾رپر‚رŒ ذ²ذ¾ذ·ذ´رƒر…ذ° ذ¸ v — رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¼رڈر‡ذ° ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½ذ¾ ذ²ذ¾ذ·ذ´رƒر…ذ°. ذر‚ذ° رپذ¸ذ»ذ° ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ° ذ؟ذµر€ذ؟ذµذ½ذ´ذ¸ذ؛رƒذ»رڈر€ذ½ذ¾ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رژ ذ¸ ذ؟ذµر€ذ؟ذµذ½ذ´ذ¸ذ؛رƒذ»رڈر€ذ½ذ¾ ذ¾رپذ¸ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ (ذ² ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸
ω د‰ -->
^ ^ -->
× أ— -->
v
^ ^ -->
{\displaystyle \textstyle {\hat {\mathbf {\omega } }}\times {\hat {\mathbf {v} }}}
[ 12]
F
M
=
1
2
ρ دپ -->
C
L
A
v
2
,
{\displaystyle F_{\text{M}}={\frac {1}{2}}\rho C_{\text{L}}Av^{2},}
ذ³ذ´ذµ دپ — ذ؟ذ»ذ¾ر‚ذ½ذ¾رپر‚رŒ ذ²ذ¾ذ·ذ´رƒر…ذ°, C L — ذ؛ذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ ذ؟ذ¾ذ´رٹر‘ذ¼ذ½ذ¾ذ¹ رپذ¸ذ»ر‹, A — ذ؟ذ»ذ¾ر‰ذ°ذ´رŒ ذ؟ذ¾ذ؟ذµر€ذµر‡ذ½ذ¾ذ³ذ¾ رپذµر‡ذµذ½ذ¸رڈ رˆذ°ر€ذ°, ذ° v — رپذ؛ذ¾ر€ذ¾رپر‚رŒ رˆذ°ر€ذ° ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½ذ¾ ذ²ذ¾ذ·ذ´رƒر…ذ°. ذڑذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ ذ؟ذ¾ذ´رٹذµذ¼ذ½ذ¾ذ¹ رپذ¸ذ»ر‹ ذ؟ر€ذµذ´رپر‚ذ°ذ²ذ»رڈذµر‚ رپذ¾ذ±ذ¾ذ¹ رپذ»ذ¾ذ¶ذ½ر‹ذ¹ ذ؟ذ°ر€ذ°ذ¼ذµر‚ر€, ذ؛ذ¾ر‚ذ¾ر€ر‹ذ¹ ذ·ذ°ذ²ذ¸رپذ¸ر‚, رپر€ذµذ´ذ¸ ذ؟ر€ذ¾ر‡ذµذ³ذ¾, ذ¾ر‚ ذ¾ر‚ذ½ذ¾رˆذµذ½ذ¸رڈ rد‰ /v , ر‡ذ¸رپذ»ذ° ذ ذµذ¹ذ½ذ¾ذ»رŒذ´رپذ° ذ¸ رˆذµر€ذ¾ر…ذ¾ذ²ذ°ر‚ذ¾رپر‚ذ¸ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸ [ 12] ذ¾ذ±ر€ذ°ر‚ذ½ر‹ذ¹ رچر„ر„ذµذ؛ر‚ ذœذ°ذ³ذ½رƒرپذ° )[ 4] [ 13] [ 14]
ذ’ ر‚ذ°ذ؛ذ¸ر… ذ²ذ¸ذ´ذ°ر… رپذ؟ذ¾ر€ر‚ذ°, ذ؛ذ°ذ؛ ر‚ذµذ½ذ½ذ¸رپ ذ¸ذ»ذ¸ ذ²ذ¾ذ»ذµذ¹ذ±ذ¾ذ» , ذ¸ذ³ر€ذ¾ذ؛ ذ¼ذ¾ذ¶ذµر‚ ذ¸رپذ؟ذ¾ذ»رŒذ·ذ¾ذ²ذ°ر‚رŒ رچر„ر„ذµذ؛ر‚ ذœذ°ذ³ذ½رƒرپذ° ذ´ذ»رڈ رƒذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸رڈ ر‚ر€ذ°ذµذ؛ر‚ذ¾ر€ذ¸ذµذ¹ ذ¼رڈر‡ذ° (ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, رپ ذ؟ذ¾ذ¼ذ¾ر‰رŒرژ ر‚ذ¾ذ؟-رپذ؟ذ¸ذ½ذ° ذ¸ذ»ذ¸ ذ¾ذ±ر€ذ°ر‚ذ½ذ¾ذ³ذ¾ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ) ذ²ذ¾ ذ²ر€ذµذ¼رڈ ذ؟ذ¾ذ»ر‘ر‚ذ°. ذ’ ذ³ذ¾ذ»رŒر„ذµ رچر‚ذ¾ر‚ رچر„ر„ذµذ؛ر‚ ذ¾ر‚ذ²ذµر‡ذ°ذµر‚ ذ·ذ° ذ½ذ°ر€ذµذ·ذ؛رƒ ذ¸ ذ·ذ°ر†ذµذ؟ , ذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ¾ذ±ر‹ر‡ذ½ذ¾ ذ½ذ°ذ½ذ¾رپرڈر‚ رƒر‰ذµر€ذ± ذ¸ذ³ر€ذ¾ذ؛رƒ ذ² ذ³ذ¾ذ»رŒر„, ذ½ذ¾ ر‚ذ°ذ؛ذ¶ذµ ذ؟ذ¾ذ¼ذ¾ذ³ذ°رژر‚ رƒذ²ذµذ»ذ¸ر‡ذ¸ر‚رŒ ذ´ذ°ذ»رŒذ½ذ¾رپر‚رŒ رƒذ´ذ°ر€ذ° ذ¸ ذ´ر€رƒذ³ذ¸ر… رƒذ´ذ°ر€ذ¾ذ²[ 15] [ 16] ذ±ذµذ¹رپذ±ذ¾ذ»ذµ ذ؟ذ¸ر‚ر‡ذµر€ر‹ ذ¸رپذ؟ذ¾ذ»رŒذ·رƒرژر‚ رچر‚ذ¾ر‚ رچر„ر„ذµذ؛ر‚ ذ´ذ»رڈ رپذ¾ذ·ذ´ذ°ذ½ذ¸رڈ ذ؛ر€رƒر‡ر‘ذ½ر‹ر… ذ¼رڈر‡ذµذ¹ ذ¸ ذ´ر€رƒذ³ذ¸ر… رپذ؟ذµر†ذ¸ذ°ذ»رŒذ½ر‹ر… ذ؟ذ¾ذ»ذµذ¹ [ 17]
ذ¤ذ°ذ»رŒرپذ¸ر„ذ¸ذ؛ذ°ر†ذ¸رڈ ذ¼رڈر‡ذ° ر‡ذ°رپر‚ذ¾ رڈذ²ذ»رڈذµر‚رپرڈ ذ½ذµذ·ذ°ذ؛ذ¾ذ½ذ½ذ¾ذ¹ ذ¸ ر‡ذ°رپر‚ذ¾ ذ¾ذ؛ذ°ذ·ر‹ذ²ذ°ذµر‚رپرڈ ذ² ر†ذµذ½ر‚ر€ذµ رپذ؟ذ¾ر€ذ¾ذ² ذ؟ذ¾ ذ؛ر€ذ¸ذ؛ذµر‚رƒ , ر‚ذ°ذ؛ذ¸ر… ذ؛ذ°ذ؛ رپذ؟ذ¾ر€ ذ¼ذµذ¶ذ´رƒ ذگذ½ذ³ذ»ذ¸ذµذ¹ ذ¸ ذںذ°ذ؛ذ¸رپر‚ذ°ذ½ذ¾ذ¼ ذ² ذ°ذ²ذ³رƒرپر‚ذµ 2006 ذ³ذ¾ذ´ذ° [ 18] رپذ؟ذ¸ر‚ذ±ذ¾ذ» آ» ذ¾ذ·ذ½ذ°ر‡ذ°ذµر‚ ذ½ذµذ·ذ°ذ؛ذ¾ذ½ذ½ذ¾ذµ ذ؟ذ¾ذ؛ر€ر‹ر‚ذ¸ذµ ذ¼رڈر‡ذ° رپذ»رژذ½ذ¾ذ¹ ذ¸ذ»ذ¸ ذ´ر€رƒذ³ذ¸ذ¼ذ¸ ذ²ذµر‰ذµرپر‚ذ²ذ°ذ¼ذ¸ رپ ر†ذµذ»رŒرژ ذ¸ذ·ذ¼ذµذ½ذµذ½ذ¸رڈ ذ°رچر€ذ¾ذ´ذ¸ذ½ذ°ذ¼ذ¸ذ؛ذ¸ ذ¼رڈر‡ذ°[ 19]
ذ›رژذ±ذ¾ذ¹ ذ¾ذ±رٹذµذ؛ر‚, ذ؟ذ¾ذ³ر€رƒذ¶ر‘ذ½ذ½ر‹ذ¹ ذ² ذ¶ذ¸ذ´ذ؛ذ¾رپر‚رŒ , ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ذ² ذ²ذ¾ذ´رƒ ذ¸ذ»ذ¸ ذ²ذ¾ذ·ذ´رƒر…, ذ±رƒذ´ذµر‚ ذ¸رپذ؟ر‹ر‚ر‹ذ²ذ°ر‚رŒ ذ؟ذ¾ذ´رٹر‘ذ¼ذ½رƒرژ رپذ¸ذ»رƒ ذ²ذ²ذµر€ر…[ 20] ذ؟ر€ذ¸ذ½ر†ذ¸ذ؟رƒ ذگر€ر…ذ¸ذ¼ذµذ´ذ° , رچر‚ذ° ذ²ر‹ر‚ذ°ذ»ذ؛ذ¸ذ²ذ°رژر‰ذ°رڈ رپذ¸ذ»ذ° ر€ذ°ذ²ذ½ذ° ذ²ذµرپرƒ ذ¶ذ¸ذ´ذ؛ذ¾رپر‚ذ¸, ذ²ر‹ر‚ذµرپذ½ذµذ½ذ½ذ¾ذ¹ ذ؟ر€ذµذ´ذ¼ذµر‚ذ¾ذ¼. ذ’ رپذ»رƒر‡ذ°ذµ رپر„ذµر€ر‹, ذ؟ذ¾ذ»ذ½ذ¾رپر‚رŒرژ ذ؟ذ¾ذ³ر€رƒذ¶ر‘ذ½ذ½ذ¾ذ¹ ذ² رپر€ذµذ´رƒ, رچر‚ذ° رپذ¸ذ»ذ° ر€ذ°ذ²ذ½ذ°
F
B
=
4
3
π د€ -->
r
3
ρ دپ -->
g
.
{\displaystyle F_{\text{B}}={\frac {4}{3}}\pi r^{3}\rho g.}
ذ’ر‹ر‚ذ°ذ»ذ؛ذ¸ذ²ذ°رژر‰ذ°رڈ رپذ¸ذ»ذ° ذ¾ذ±ر‹ر‡ذ½ذ¾ ذ¼ذ°ذ»ذ° ذ؟ذ¾ رپر€ذ°ذ²ذ½ذµذ½ذ¸رژ رپ رپذ¾ذ؟ر€ذ¾ر‚ذ¸ذ²ذ»ذµذ½ذ¸ذµذ¼ ذ¸ رپذ¸ذ»ذ°ذ¼ذ¸ ذœذ°ذ³ذ½رƒرپذ°, ذ¸ ذµرژ ر‡ذ°رپر‚ذ¾ ذ¼ذ¾ذ¶ذ½ذ¾ ذ؟ر€ذµذ½ذµذ±ر€ذµر‡رŒ. ذذ´ذ½ذ°ذ؛ذ¾ ذ² رپذ»رƒر‡ذ°ذµ رپ ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ر‹ذ¼ ذ¼رڈر‡ذ¾ذ¼ ذ²ر‹ر‚ذ°ذ»ذ؛ذ¸ذ²ذ°رژر‰ذ°رڈ رپذ¸ذ»ذ° ذ¼ذ¾ذ¶ذµر‚ رپذ¾رپر‚ذ°ذ²ذ»رڈر‚رŒ ذ¾ذ؛ذ¾ذ»ذ¾ 1,5 % ذ²ذµرپذ° ذ¼رڈر‡ذ°[ 20]
ذ،ذ¶ذ°ر‚ذ¸ذµ (A→B) ذ¸ ذ´ذµذ؛ذ¾ذ¼ذ؟ر€ذµرپرپذ¸رڈ (B→C) ذ¼رڈر‡ذ°, رƒذ´ذ°ر€رڈرژر‰ذµذ³ذ¾رپرڈ ذ¾ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ. ذ،ذ¸ذ»ذ° رƒذ´ذ°ر€ذ° ذ¾ذ±ر‹ر‡ذ½ذ¾ ذ؟ر€ذ¾ذ؟ذ¾ر€ر†ذ¸ذ¾ذ½ذ°ذ»رŒذ½ذ° ر€ذ°رپرپر‚ذ¾رڈذ½ذ¸رژ رپذ¶ذ°ر‚ذ¸رڈ, ذ؟ذ¾ ذ؛ر€ذ°ذ¹ذ½ذµذ¹ ذ¼ذµر€ذµ, ذ؟ر€ذ¸ ذ½ذµذ±ذ¾ذ»رŒرˆذ¸ر… رپذ¶ذ°ر‚ذ¸رڈر…, ذ¸ ذµر‘ ذ¼ذ¾ذ¶ذ½ذ¾ ذ¼ذ¾ذ´ذµذ»ذ¸ر€ذ¾ذ²ذ°ر‚رŒ ذ؟ذ¾ ذ·ذ°ذ؛ذ¾ذ½رƒ ذ“رƒذ؛ذ° ذ´ذ»رڈ ذ؟ر€رƒذ¶ذ¸ذ½ر‹ [ 21] [ 22] ذڑذ¾ذ³ذ´ذ° ذ¼رڈر‡ رƒذ´ذ°ر€رڈذµر‚رپرڈ ذ¾ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ, ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ ذ´ذµر„ذ¾ر€ذ¼ذ¸ر€رƒذµر‚رپرڈ ذ¸ ذ²ذ¸ذ±ر€ذ¸ر€رƒذµر‚ , ذ؛ذ°ذ؛ ذ¸ ذ¼رڈر‡, رپذ¾ذ·ذ´ذ°ذ²ذ°رڈ ذ·ذ²رƒذ؛ ذ¸ ر‚ذµذ؟ذ»ذ¾ , ذ° ذ¼رڈر‡ ر‚ذµر€رڈذµر‚ ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛رƒرژ رچذ½ذµر€ذ³ذ¸رژ . ذڑر€ذ¾ذ¼ذµ ر‚ذ¾ذ³ذ¾, رƒذ´ذ°ر€ ذ¼ذ¾ذ¶ذµر‚ ذ؟ر€ذ¸ذ´ذ°ر‚رŒ رˆذ°ر€رƒ ذ½ذµذ؛ذ¾ر‚ذ¾ر€ذ¾ذµ ذ²ر€ذ°ر‰ذµذ½ذ¸ذµ, ذ؟ر€ذµذ¾ذ±ر€ذ°ذ·رƒرڈ ر‡ذ°رپر‚رŒ ذµذ³ذ¾ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ذ¾ذ¹ ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛ذ¾ذ¹ رچذ½ذµر€ذ³ذ¸ذ¸ ذ² ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛رƒرژ رچذ½ذµر€ذ³ذ¸رژ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ . ذر‚ذ¸ ذ؟ذ¾ر‚ذµر€ذ¸ رچذ½ذµر€ذ³ذ¸ذ¸ ذ¾ذ±ر‹ر‡ذ½ذ¾ ر…ذ°ر€ذ°ذ؛ر‚ذµر€ذ¸ذ·رƒرژر‚رپرڈ (ذ؛ذ¾رپذ²ذµذ½ذ½ذ¾) ر‡ذµر€ذµذ· ذ؛ذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ ذ²ذ¾رپرپر‚ذ°ذ½ذ¾ذ²ذ»ذµذ½ذ¸رڈ (ذ¸ذ»ذ¸ COR, ذ¾ذ±ذ¾ذ·ذ½ذ°ر‡ذ°ذµذ¼ر‹ذ¹ e )[ 23] [ note 1]
e
=
− − -->
v
f
− − -->
u
f
v
i
− − -->
u
i
,
{\displaystyle e=-{\frac {v_{\text{f}}-u_{\text{f}}}{v_{\text{i}}-u_{\text{i}}}},}
ذ³ذ´ذµ v f ذ¸ vi — ذ؛ذ¾ذ½ذµر‡ذ½ذ°رڈ ذ¸ ذ½ذ°ر‡ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚ذ¸ ذ¼رڈر‡ذ°, ذ° u f ذ¸ u i — ذ؛ذ¾ذ½ذµر‡ذ½ذ°رڈ ذ¸ ذ½ذ°ر‡ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚ذ¸ رƒذ´ذ°ر€رڈرژر‰ذµذ¹رپرڈ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸ رپذ¾ذ¾ر‚ذ²ذµر‚رپر‚ذ²ذµذ½ذ½ذ¾. ذ’ ذ؛ذ¾ذ½ذ؛ر€ذµر‚ذ½ذ¾ذ¼ رپذ»رƒر‡ذ°ذµ, ذ؛ذ¾ذ³ذ´ذ° ذ¼رڈر‡ رƒذ´ذ°ر€رڈذµر‚رپرڈ ذ¾ ذ½ذµذ؟ذ¾ذ´ذ²ذ¸ذ¶ذ½رƒرژ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ, COR رƒذ؟ر€ذ¾ر‰ذ°ذµر‚رپرڈ ذ´ذ¾
e
=
− − -->
v
f
v
i
.
{\displaystyle e=-{\frac {v_{\text{f}}}{v_{\text{i}}}}.}
ذ¢ذ°ذ؛ذ¸ذ¼ ذ¾ذ±ر€ذ°ذ·ذ¾ذ¼, ذ´ذ»رڈ ذ¼رڈر‡ذ°, رƒذ؟ذ°ذ²رˆذµذ³ذ¾ ذ½ذ° ذ؟ذ¾ذ», COR ذ±رƒذ´ذµر‚ ذ²ذ°ر€رŒذ¸ر€ذ¾ذ²ذ°ر‚رŒرپرڈ ذ¾ر‚ 0 (ذ½ذµر‚ ذ¾ر‚رپذ؛ذ¾ذ؛ذ°, ذ؟ذ¾ذ»ذ½ذ°رڈ ذ؟ذ¾ر‚ذµر€رڈ رچذ½ذµر€ذ³ذ¸ذ¸) ذ´ذ¾ 1 (ذ¸ذ´ذµذ°ذ»رŒذ½ر‹ذ¹ ذ¾ر‚رپذ؛ذ¾ذ؛, ذ¾ر‚رپرƒر‚رپر‚ذ²ذ¸ذµ ذ؟ذ¾ر‚ذµر€ذ¸ رچذ½ذµر€ذ³ذ¸ذ¸). ذ—ذ½ذ°ر‡ذµذ½ذ¸ذµ COR ذ½ذ¸ذ¶ذµ 0 ذ¸ذ»ذ¸ ذ²ر‹رˆذµ 1 ر‚ذµذ¾ر€ذµر‚ذ¸ر‡ذµرپذ؛ذ¸ ذ²ذ¾ذ·ذ¼ذ¾ذ¶ذ½ذ¾, ذ½ذ¾ ذ±رƒذ´ذµر‚ رƒذ؛ذ°ذ·ر‹ذ²ذ°ر‚رŒ ذ½ذ° ر‚ذ¾, ر‡ر‚ذ¾ ذ¼رڈر‡ ذ؟ر€ذ¾رˆذµذ» ر‡ذµر€ذµذ· ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ (e < 0e > 1
ذ§ر‚ذ¾ذ±ر‹ ذ؟ر€ذ¾ذ°ذ½ذ°ذ»ذ¸ذ·ذ¸ر€ذ¾ذ²ذ°ر‚رŒ ذ²ذµر€ر‚ذ¸ذ؛ذ°ذ»رŒذ½ر‹ذµ ذ¸ ذ³ذ¾ر€ذ¸ذ·ذ¾ذ½ر‚ذ°ذ»رŒذ½ر‹ذµ ذ؛ذ¾ذ¼ذ؟ذ¾ذ½ذµذ½ر‚ر‹ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ, COR ذ¸ذ½ذ¾ذ³ذ´ذ° ر€ذ°ذ·ذ´ذµذ»رڈرژر‚ ذ½ذ° ذ؟ر€ذ¾ذµذ؛ر†ذ¸ذ¸: ذ½ذ¾ر€ذ¼ذ°ذ»رŒذ½ر‹ذ¹ e y ) ذ¸ ر‚ذ°ذ½ذ³ذµذ½ر†ذ¸ذ°ذ»رŒذ½ر‹ذ¹ e x ), ذ¾ذ؟ر€ذµذ´ذµذ»رڈذµذ¼ر‹ذµ ذ؛ذ°ذ؛[ 24]
e
y
=
− − -->
v
yf
− − -->
u
yf
v
yi
− − -->
u
yi
,
{\displaystyle e_{\text{y}}=-{\frac {v_{\text{yf}}-u_{\text{yf}}}{v_{\text{yi}}-u_{\text{yi}}}},}
e
x
=
− − -->
(
v
xf
− − -->
r
ω د‰ -->
f
)
− − -->
(
u
xf
− − -->
R
Ω خ© -->
f
)
(
v
xi
− − -->
r
ω د‰ -->
i
)
− − -->
(
u
xi
− − -->
R
Ω خ© -->
i
)
,
{\displaystyle e_{\text{x}}=-{\frac {(v_{\text{xf}}-r\omega _{\text{f}})-(u_{\text{xf}}-R\Omega _{\text{f}})}{(v_{\text{xi}}-r\omega _{\text{i}})-(u_{\text{xi}}-R\Omega _{\text{i}})}},}
ذ³ذ´ذµ r ذ¸ د‰ — ر€ذ°ذ´ذ¸رƒرپ ذ¸ رƒذ³ذ»ذ¾ذ²رƒرژ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¼رڈر‡ذ°, ذ° R ذ¸ خ© — ر€ذ°ذ´ذ¸رƒرپ ذ¸ رƒذ³ذ»ذ¾ذ²رƒرژ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸ رƒذ´ذ°ر€ذ° (ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ذ±ذµذ¹رپذ±ذ¾ذ»رŒذ½ذ¾ذ¹ ذ±ذ¸ر‚ر‹). ذ’ ر‡ذ°رپر‚ذ½ذ¾رپر‚ذ¸ , rد‰ — رچر‚ذ¾ ر‚ذ°ذ½ذ³ذµذ½ر†ذ¸ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸ رˆذ°ر€ذ°, ذ° Rخ© — رچر‚ذ¾ ر‚ذ°ذ½ذ³ذµذ½ر†ذ¸ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ رپذ¾رƒذ´ذ°ر€رڈرژر‰ذµذ¹رپرڈ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸. ذر‚ذ¾ ذ¾رپذ¾ذ±ذµذ½ذ½ذ¾ ذ²ذ°ذ¶ذ½ذ¾, ذ؛ذ¾ذ³ذ´ذ° ذ¼رڈر‡ رƒذ´ذ°ر€رڈذµر‚رپرڈ ذ¾ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ ذ؟ذ¾ذ´ ذ؛ذ¾رپر‹ذ¼ رƒذ³ذ»ذ¾ذ¼ ذ¸ذ»ذ¸ ذ؛ذ¾ذ³ذ´ذ° ذ·ذ°ذ´ذµذ¹رپر‚ذ²ذ¾ذ²ذ°ذ½ذ¾ ذ²ر€ذ°ر‰ذµذ½ذ¸ذµ .
ذںر€ذ¸ ذ؟ر€رڈذ¼ذ¾ذ¼ ذ؟ذ°ذ´ذµذ½ذ¸ذ¸ ذ½ذ° ذ·ذµذ¼ذ»رژ ذ±ذµذ· ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ, ذ؛ذ¾ذ³ذ´ذ° ذ½ذ° ذ¼رڈر‡ ذ´ذµذ¹رپر‚ذ²رƒذµر‚ ر‚ذ¾ذ»رŒذ؛ذ¾ رپذ¸ذ»ذ° ر‚رڈذ¶ذµرپر‚ذ¸, COR ذ¼ذ¾ذ¶ذ½ذ¾ رپذ²رڈذ·ذ°ر‚رŒ رپ ذ½ذµرپذ؛ذ¾ذ»رŒذ؛ذ¸ذ¼ذ¸ ذ´ر€رƒذ³ذ¸ذ¼ذ¸ ذ²ذµذ»ذ¸ر‡ذ¸ذ½ذ°ذ¼ذ¸ رپذ»ذµذ´رƒرژر‰ذ¸ذ¼ ذ¾ذ±ر€ذ°ذ·ذ¾ذ¼[ 22] [ 25]
e
=
|
v
f
v
i
|
=
K
f
K
i
=
U
f
U
i
=
H
f
H
i
=
T
f
T
i
=
g
T
f
2
8
H
i
.
{\displaystyle e=\left|{\frac {v_{\text{f}}}{v_{\text{i}}}}\right|={\sqrt {\frac {K_{\text{f}}}{K_{\text{i}}}}}={\sqrt {\frac {U_{\text{f}}}{U_{\text{i}}}}}={\sqrt {\frac {H_{\text{f}}}{H_{\text{i}}}}}={\frac {T_{\text{f}}}{T_{\text{i}}}}={\sqrt {\frac {gT_{\text{f}}^{2}}{8H_{\text{i}}}}}.}
ذ—ذ´ذµرپرŒ K ذ¸ U ذ¾ذ±ذ¾ذ·ذ½ذ°ر‡ذ°رژر‚ ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛رƒرژ ذ¸ ذ؟ذ¾ر‚ذµذ½ر†ذ¸ذ°ذ»رŒذ½رƒرژ رچذ½ذµر€ذ³ذ¸رژ ذ¼رڈر‡ذ°, H — ذ¼ذ°ذ؛رپذ¸ذ¼ذ°ذ»رŒذ½رƒرژ ذ²ر‹رپذ¾ر‚رƒ ذ¼رڈر‡ذ°, ذ° T — ذ²ر€ذµذ¼رڈ ذ؟ذ¾ذ»ذµر‚ذ° ذ¼رڈر‡ذ°. ذکذ½ذ´ذµذ؛رپر‹ آ«iآ» ذ¸ آ«fآ» ذ¾ر‚ذ½ذ¾رپرڈر‚رپرڈ ذ؛ ذ½ذ°ر‡ذ°ذ»رŒذ½ذ¾ذ¼رƒ (ذ´ذ¾ رƒذ´ذ°ر€ذ°) ذ¸ ذ؛ذ¾ذ½ذµر‡ذ½ذ¾ذ¼رƒ (ذ؟ذ¾رپذ»ذµ رƒذ´ذ°ر€ذ°) رپذ¾رپر‚ذ¾رڈذ½ذ¸رڈذ¼ ذ¼رڈر‡ذ°. ذگذ½ذ°ذ»ذ¾ذ³ذ¸ر‡ذ½ر‹ذ¼ ذ¾ذ±ر€ذ°ذ·ذ¾ذ¼, ذ؟ذ¾ر‚ذµر€رژ رچذ½ذµر€ذ³ذ¸ذ¸ ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ ذ¼ذ¾ذ¶ذ½ذ¾ رپذ²رڈذ·ذ°ر‚رŒ رپ COR رپذ¾ذ¾ر‚ذ½ذ¾رˆذµذ½ذ¸ذµذ¼
Energy Loss
=
K
i
− − -->
K
f
K
i
× أ— -->
100
% % -->
=
(
1
− − -->
e
2
)
× أ— -->
100
% % -->
.
{\displaystyle {\text{Energy Loss}}={\frac {{K_{\text{i}}}-{K_{\text{f}}}}{K_{\text{i}}}}\times 100\%=\left(1-e^{2}\right)\times 100\%.}
ذذ° COR ذ¼رڈر‡ذ° ذ¼ذ¾ذ³رƒر‚ ذ²ذ»ذ¸رڈر‚رŒ ذ½ذµرپذ؛ذ¾ذ»رŒذ؛ذ¾ ر„ذ°ذ؛ر‚ذ¾ر€ذ¾ذ², ذ² ذ¾رپذ½ذ¾ذ²ذ½ذ¾ذ¼
ر…ذ°ر€ذ°ذ؛ر‚ذµر€ ذ²ذ¾ذ·ذ´ذµذ¹رپر‚ذ²رƒرژر‰ذµذ¹ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸ (ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ر‚ر€ذ°ذ²ذ°, ذ±ذµر‚ذ¾ذ½, ذ؟ر€ذ¾ذ²ذ¾ذ»ذ¾ر‡ذ½ذ°رڈ رپذµر‚ذ؛ذ°)[ 25] [ 26]
ذ¼ذ°ر‚ذµر€ذ¸ذ°ذ» ذ¼رڈر‡ذ° (ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ذ؛ذ¾ذ¶ذ°, ر€ذµذ·ذ¸ذ½ذ°, ذ؟ذ»ذ°رپر‚ذ¸ذ؛)[ 22]
ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ذ²ذ½رƒر‚ر€ذ¸ رˆذ°ر€ذ° (ذµرپذ»ذ¸ ذ؟ذ¾ذ»ر‹ذ¹)[ 22]
ذ²ذµذ»ذ¸ر‡ذ¸ذ½ذ° ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ, ذ²ذ¾ذ·ذ½ذ¸ذ؛ذ°رژر‰ذ°رڈ ذ² ذ¼رڈر‡ذµ ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ[ 27]
رپذ؛ذ¾ر€ذ¾رپر‚رŒ رƒذ´ذ°ر€ذ°[ 21] [ 22] [ 26] [ 28] ذ’ذ½ذµرˆذ½ذ¸ذµ رƒرپذ»ذ¾ذ²ذ¸رڈ, ر‚ذ°ذ؛ذ¸ذµ ذ؛ذ°ذ؛ ر‚ذµذ¼ذ؟ذµر€ذ°ر‚رƒر€ذ° , ذ¼ذ¾ذ³رƒر‚ ذ¸ذ·ذ¼ذµذ½ذ¸ر‚رŒ رپذ²ذ¾ذ¹رپر‚ذ²ذ° رƒذ´ذ°ر€رڈرژر‰ذµذ¹رپرڈ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸ ذ¸ذ»ذ¸ ذ¼رڈر‡ذ°, ذ´ذµذ»ذ°رڈ ذ¸ر… ذ±ذ¾ذ»ذµذµ ذ³ذ¸ذ±ذ؛ذ¸ذ¼ذ¸ ذ¸ذ»ذ¸ ذ±ذ¾ذ»ذµذµ ذ¶ر‘رپر‚ذ؛ذ¸ذ¼ذ¸. ذر‚ذ¾, ذ² رپذ²ذ¾رژ ذ¾ر‡ذµر€ذµذ´رŒ, ذ؟ذ¾ذ²ذ»ذ¸رڈذµر‚ ذ½ذ° COR[ 22] [ 22] [ 28]
ذ،ذ¸ذ»ر‹, ذ´ذµذ¹رپر‚ذ²رƒرژر‰ذ¸ذµ ذ½ذ° ذ²ر€ذ°ر‰ذ°رژر‰ذ¸ذ¹رپرڈ ذ¼رڈر‡ ذ²ذ¾ ذ²ر€ذµذ¼رڈ رƒذ´ذ°ر€ذ°, — رچر‚ذ¾ رپذ¸ذ»ذ° ر‚رڈذ¶ذµرپر‚ذ¸ , ذ½ذ¾ر€ذ¼ذ°ذ»رŒذ½ذ°رڈ رپذ¸ذ»ذ° ذ¸ رپذ¸ذ»ذ° ر‚ر€ذµذ½ذ¸رڈ (ذ؛ذ¾ر‚ذ¾ر€ذ°رڈ ذ¾ذ±ر‹ر‡ذ½ذ¾ ذ¸ذ¼ذµذµر‚ ذ؛ذ°ذ؛ آ«ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½رƒرژآ», ر‚ذ°ذ؛ ذ¸ آ«ذ²ر€ذ°ر‰ذ°ر‚ذµذ»رŒذ½رƒرژآ» رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰رƒرژ). ذ•رپذ»ذ¸ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ ذ½ذ°ذ؛ذ»ذ¾ذ½ذµذ½ذ°, ر‚ذ¾ رپذ¸ذ»ذ° ر‚رڈذ¶ذµرپر‚ذ¸ ذ±رƒذ´ذµر‚ ذ½ذ°ر…ذ¾ذ´ذ¸ر‚رŒرپرڈ ذ؟ذ¾ذ´ رƒذ³ذ»ذ¾ذ¼ ذ؛ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸, ذ² ر‚ذ¾ ذ²ر€ذµذ¼رڈ ذ؛ذ°ذ؛ ذ´ر€رƒذ³ذ¸ذµ رپذ¸ذ»ر‹ ذ¾رپر‚ذ°ذ½رƒر‚رپرڈ ذ؟ذµر€ذ؟ذµذ½ذ´ذ¸ذ؛رƒذ»رڈر€ذ½ر‹ذ¼ذ¸ ذ¸ذ»ذ¸ ذ؟ذ°ر€ذ°ذ»ذ»ذµذ»رŒذ½ر‹ذ¼ذ¸ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸. ذںر€ذ¸ رƒذ´ذ°ر€ذµ ذ¾ ذ·ذµذ¼ذ»رژ ذ½ذµذ؛ذ¾ر‚ذ¾ر€ذ°رڈ ر‡ذ°رپر‚رŒ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ذ¾ذ¹ ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛ذ¾ذ¹ رچذ½ذµر€ذ³ذ¸ذ¸ ذ¼ذ¾ذ¶ذµر‚ ذ±ر‹ر‚رŒ ذ؟ر€ذµذ¾ذ±ر€ذ°ذ·ذ¾ذ²ذ°ذ½ذ° ذ² ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛رƒرژ رچذ½ذµر€ذ³ذ¸رژ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ذ¸ ذ½ذ°ذ¾ذ±ذ¾ر€ذ¾ر‚, ذ² ذ·ذ°ذ²ذ¸رپذ¸ذ¼ذ¾رپر‚ذ¸ ذ¾ر‚ رƒذ³ذ»ذ° رƒذ´ذ°ر€ذ° ذ¼رڈر‡ذ° ذ¸ رƒذ³ذ»ذ¾ذ²ذ¾ذ¹ رپذ؛ذ¾ر€ذ¾رپر‚ذ¸. ذ•رپذ»ذ¸ ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ ذ¼رڈر‡ ذ´ذ²ذ¸ذ¶ذµر‚رپرڈ ذ³ذ¾ر€ذ¸ذ·ذ¾ذ½ر‚ذ°ذ»رŒذ½ذ¾, ر‚ر€ذµذ½ذ¸ذµ ذ±رƒذ´ذµر‚ ذ¸ذ¼ذµر‚رŒ آ«ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½رƒرژآ» رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰رƒرژ ذ² ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸, ذ؟ر€ذ¾ر‚ذ¸ذ²ذ¾ذ؟ذ¾ذ»ذ¾ذ¶ذ½ذ¾ذ¼ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رژ ذ¼رڈر‡ذ°. ذذ° ر€ذ¸رپرƒذ½ذ؛ذµ ذ¼رڈر‡ ذ´ذ²ذ¸ذ¶ذµر‚رپرڈ ذ²ذ؟ر€ذ°ذ²ذ¾ , ذ¸, رپذ»ذµذ´ذ¾ذ²ذ°ر‚ذµذ»رŒذ½ذ¾, رƒ ذ½ذµذ³ذ¾ ذ±رƒذ´ذµر‚ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ذ°رڈ رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰ذ°رڈ ر‚ر€ذµذ½ذ¸رڈ, ر‚ذ¾ذ»ذ؛ذ°رژر‰ذ°رڈ ذ¼رڈر‡ ذ²ذ»ذµذ²ذ¾ . ذڑر€ذ¾ذ¼ذµ ر‚ذ¾ذ³ذ¾, ذµرپذ»ذ¸ ذ¼رڈر‡ ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ ذ²ر€ذ°ر‰ذ°ذµر‚رپرڈ, ر‚ر€ذµذ½ذ¸ذµ ذ±رƒذ´ذµر‚ ذ¸ذ¼ذµر‚رŒ آ«ذ²ر€ذ°ر‰ذ°ر‚ذµذ»رŒذ½رƒرژآ» رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰رƒرژ ذ² ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸, ذ؟ر€ذ¾ر‚ذ¸ذ²ذ¾ذ؟ذ¾ذ»ذ¾ذ¶ذ½ذ¾ذ¼ ذ²ر€ذ°ر‰ذµذ½ذ¸رژ ذ¼رڈر‡ذ°. ذذ° ر€ذ¸رپرƒذ½ذ؛ذµ ذ¼رڈر‡ ذ²ر€ذ°ر‰ذ°ذµر‚رپرڈ ذ؟ذ¾ ر‡ذ°رپذ¾ذ²ذ¾ذ¹ رپر‚ر€ذµذ»ذ؛ذµ, ذ° ر‚ذ¾ر‡ذ؛ذ° رƒذ´ذ°ر€ذ° ذ¾ ذ·ذµذ¼ذ»رژ ذ؟ذµر€ذµذ¼ذµر‰ذ°ذµر‚رپرڈ ذ²ذ»ذµذ²ذ¾ ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½ذ¾ ر†ذµذ½ر‚ر€ذ° ذ¼ذ°رپرپ ذ¼رڈر‡ذ°. ذ¢ذ°ذ؛ذ¸ذ¼ ذ¾ذ±ر€ذ°ذ·ذ¾ذ¼, ذ²ر€ذ°ر‰ذ°ر‚ذµذ»رŒذ½ذ°رڈ رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰ذ°رڈ ر‚ر€ذµذ½ذ¸رڈ ر‚ذ¾ذ»ذ؛ذ°ذµر‚ ذ¼رڈر‡ ذ²ذ؟ر€ذ°ذ²ذ¾ . ذ’ ذ¾ر‚ذ»ذ¸ر‡ذ¸ذµ ذ¾ر‚ ذ½ذ¾ر€ذ¼ذ°ذ»رŒذ½ذ¾ذ¹ رپذ¸ذ»ر‹ ذ¸ رپذ¸ذ»ر‹ ر‚رڈذ¶ذµرپر‚ذ¸, رچر‚ذ¸ رپذ¸ذ»ر‹ ر‚ر€ذµذ½ذ¸رڈ ذ¾ذ؛ذ°ذ·ر‹ذ²ذ°رژر‚ ذ½ذ° رˆذ°ر€ ذ؛ر€رƒر‚رڈر‰ذ¸ذ¹ ذ¼ذ¾ذ¼ذµذ½ر‚ ذ¸ ذ¸ذ·ذ¼ذµذ½رڈرژر‚ ذµذ³ذ¾ رƒذ³ذ»ذ¾ذ²رƒرژ رپذ؛ذ¾ر€ذ¾رپر‚رŒ (د‰ )[ 29] [ 30] [ 31] [ 32]
ذœذ¾ذ³رƒر‚ ذ²ذ¾ذ·ذ½ذ¸ذ؛ذ½رƒر‚رŒ ر‚ر€ذ¸ رپذ¸ر‚رƒذ°ر†ذ¸ذ¸[ 32] [ 33] [ 34]
ذ•رپذ»ذ¸ ذ¼رڈر‡ ذ´ذ²ذ¸ذ¶ذµر‚رپرڈ ذ²ذ؟ذµر€ذµذ´ رپ ذ¾ذ±ر€ذ°ر‚ذ½ر‹ذ¼ ذ²ر€ذ°ر‰ذµذ½ذ¸ذµذ¼ ذ²ذ²ذµر€ر… , ذ²ذ¾ذ·ذ¼ذ¾ذ¶ذ½ذ¾, ذ´ذ°ذ¶ذµ ذ؟ر€ذµذ²ر‹رپذ¸ذ² رپذ²ذ¾رژ ذ؟ذµر€ذ²ذ¾ذ½ذ°ر‡ذ°ذ»رŒذ½رƒرژ ذ²ر‹رپذ¾ر‚رƒ. ذ¢ذ°ذ؛ذ¶ذµ ذ²ذ¾ذ·ذ¼ذ¾ذ¶ذ½ذ¾, ر‡ر‚ذ¾ ذ¼رڈر‡ ذ½ذ°ر‡ذ½ر‘ر‚ ذ²ر€ذ°ر‰ذ°ر‚رŒرپرڈ ذ² ذ؟ر€ذ¾ر‚ذ¸ذ²ذ¾ذ؟ذ¾ذ»ذ¾ذ¶ذ½ذ¾ذ¼ ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸ ذ¸ ذ´ذ°ذ¶ذµ ذ¾ر‚رپذ؛ذ¾ر‡ذ¸ر‚ ذ½ذ°ذ·ذ°ذ´.
ذ•رپذ»ذ¸ ذ¼رڈر‡ ذ´ذ²ذ¸ذ¶ذµر‚رپرڈ ذ²ذ؟ذµر€ذµذ´ رپ ر‚ذ¾ذ؟-رپذ؟ذ¸ذ½ذ¾ذ¼ ذ•رپذ»ذ¸ ذ¼رڈر‡ ذ²ر€ذ°ر‰ذ°ذµر‚رپرڈ ذ³ذ¾ر€ذ°ذ·ذ´ذ¾ ذ±ر‹رپر‚ر€ذµذµ, ر‡ذµذ¼ ذ´ذ²ذ¸ذ³ذ°ذ»رپرڈ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ذ¾, ر‚ذ¾ ر‚ر€ذµذ½ذ¸ذµ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ذ±رƒذ´ذµر‚ ذ؟ر€ذµذ¾ذ±ذ»ذ°ذ´ذ°ر‚رŒ. ذ£ذ³ذ»ذ¾ذ²ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¼رڈر‡ذ° ذ؟ذ¾رپذ»ذµ رƒذ´ذ°ر€ذ° رƒذ¼ذµذ½رŒرˆذ¸ر‚رپرڈ, ذ½ذ¾ ذµذ³ذ¾ ذ³ذ¾ر€ذ¸ذ·ذ¾ذ½ر‚ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ رƒذ²ذµذ»ذ¸ر‡ذ¸ر‚رپرڈ. ذœرڈر‡ ذ±رƒذ´ذµر‚ ذ´ذ²ذ¸ذ³ذ°ر‚رŒرپرڈ ذ²ذ؟ذµر€ر‘ذ´ , ذ½ذ¾ ذ½ذµ ذ؟ر€ذµذ²ر‹رپذ¸ر‚ رپذ²ذ¾ذµذ¹ ذ؟ذµر€ذ²ذ¾ذ½ذ°ر‡ذ°ذ»رŒذ½ذ¾ذ¹ ذ²ر‹رپذ¾ر‚ر‹ ذ¸ ذ؟ر€ذ¾ذ´ذ¾ذ»ذ¶ذ¸ر‚ ذ²ر€ذ°ر‰ذ°ر‚رŒرپرڈ ذ² ر‚ذ¾ذ¼ ذ¶ذµ ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸.
ذ•رپذ»ذ¸ ذ¼رڈر‡ ذ´ذ²ذ¸ذ¶ذµر‚رپرڈ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ذ¾ ذ³ذ¾ر€ذ°ذ·ذ´ذ¾ ذ±ر‹رپر‚ر€ذµذµ, ر‡ذµذ¼ ذ²ر€ذ°ر‰ذ°ذ»رپرڈ, ر‚ذ¾ ر‚ر€ذµذ½ذ¸ذµ, رپذ²رڈذ·ذ°ذ½ذ½ذ¾ذµ رپ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ر‹ذ¼ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸ذµذ¼ ذ±رƒذ´ذµر‚ ذ؟ر€ذµذ¾ذ±ذ»ذ°ذ´ذ°ر‚رŒ. ذ£ذ³ذ»ذ¾ذ²ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¼رڈر‡ذ° ذ؟ذ¾رپذ»ذµ رƒذ´ذ°ر€ذ° رƒذ²ذµذ»ذ¸ر‡ذ¸ر‚رپرڈ, ذ½ذ¾ ذµذ³ذ¾ ذ³ذ¾ر€ذ¸ذ·ذ¾ذ½ر‚ذ°ذ»رŒذ½ذ°رڈ رپذ؛ذ¾ر€ذ¾رپر‚رŒ رƒذ¼ذµذ½رŒرˆذ¸ر‚رپرڈ. ذœرڈر‡ ذ½ذµ ذ؟ر€ذµذ²ر‹رپذ¸ر‚ رپذ²ذ¾رژ ذ؟ذµر€ذ²ذ¾ذ½ذ°ر‡ذ°ذ»رŒذ½رƒرژ ذ²ر‹رپذ¾ر‚رƒ ذ¸ ذ؟ر€ذ¾ذ´ذ¾ذ»ذ¶ذ¸ر‚ ذ²ر€ذ°ر‰ذ°ر‚رŒرپرڈ ذ² ر‚ذ¾ذ¼ ذ¶ذµ ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذ¸. ذ•رپذ»ذ¸ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ ذ½ذ°ذ؛ذ»ذ¾ذ½ذµذ½ذ° ذ½ذ° ذ½ذµذ؛ذ¾ر‚ذ¾ر€رƒرژ ذ²ذµذ»ذ¸ر‡ذ¸ذ½رƒ خ¸ , ذ²رپرڈ ذ´ذ¸ذ°ذ³ر€ذ°ذ¼ذ¼ذ° ذ؟ذ¾ذ²ذµر€ذ½ر‘ر‚رپرڈ ذ½ذ° خ¸ , ذ½ذ¾ رپذ¸ذ»ذ° ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸ذ¸ ذ¾رپر‚ذ°ذ½ذµر‚رپرڈ ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ½ذ¾ذ¹ ذ²ذ½ذ¸ذ· (ذ¾ذ±ر€ذ°ذ·رƒرڈ رƒذ³ذ¾ذ» خ¸ رپ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒرژ). ذ¢ذ¾ذ³ذ´ذ° ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸رڈ ذ±رƒذ´ذµر‚ ذ¸ذ¼ذµر‚رŒ ذ؛ذ¾ذ¼ذ؟ذ¾ذ½ذµذ½ر‚رƒ, ذ؟ذ°ر€ذ°ذ»ذ»ذµذ»رŒذ½رƒرژ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذ¸, ذ؛ذ¾ر‚ذ¾ر€ر‹ذ¹ ذ±رƒذ´ذµر‚ رپذ؟ذ¾رپذ¾ذ±رپر‚ذ²ذ¾ذ²ذ°ر‚رŒ ر‚ر€ذµذ½ذ¸رژ ذ¸, ر‚ذ°ذ؛ذ¸ذ¼ ذ¾ذ±ر€ذ°ذ·ذ¾ذ¼, رپذ؟ذ¾رپذ¾ذ±رپر‚ذ²ذ¾ذ²ذ°ر‚رŒ ذ²ر€ذ°ر‰ذµذ½ذ¸رژ[ 32]
ذ’ ذ²ذ¸ذ´ذ°ر… رپذ؟ذ¾ر€ر‚ذ° رپ ر€ذ°ذ؛ذµر‚ذ؛ذ°ذ¼ذ¸ , ر‚ذ°ذ؛ذ¸ر… ذ؛ذ°ذ؛ ذ½ذ°رپر‚ذ¾ذ»رŒذ½ر‹ذ¹ ر‚ذµذ½ذ½ذ¸رپ ذ¸ذ»ذ¸ ر€ذ°ذ؛ذµر‚ذ±ذ¾ذ» , ذ¾ذ؟ر‹ر‚ذ½ر‹ذµ ذ¸ذ³ر€ذ¾ذ؛ذ¸ ذ±رƒذ´رƒر‚ ذ¸رپذ؟ذ¾ذ»رŒذ·ذ¾ذ²ذ°ر‚رŒ ذ²ر€ذ°ر‰ذµذ½ذ¸ذµ (ذ²ذ؛ذ»رژر‡ذ°رڈ ذ±ذ¾ذ؛ذ¾ذ²ذ¾ذµ ذ²ر€ذ°ر‰ذµذ½ذ¸ذµ ), ر‡ر‚ذ¾ذ±ر‹ ذ²ذ½ذµذ·ذ°ذ؟ذ½ذ¾ ذ¸ذ·ذ¼ذµذ½ذ¸ر‚رŒ ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذµ ذ¼رڈر‡ذ°, ذ؛ذ¾ذ³ذ´ذ° ذ¾ذ½ رƒذ´ذ°ر€رڈذµر‚رپرڈ ذ¾ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ, ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ذ¾ ذ·ذµذ¼ذ»رژ ذ¸ذ»ذ¸ ر€ذ°ذ؛ذµر‚ذ؛رƒ ذ؟ر€ذ¾ر‚ذ¸ذ²ذ½ذ¸ذ؛ذ°. ذ¢ذ¾ر‡ذ½ذ¾ ر‚ذ°ذ؛ ذ¶ذµ ذ² ذ؛ر€ذ¸ذ؛ذµر‚ذµ رپرƒر‰ذµرپر‚ذ²رƒرژر‚ ر€ذ°ذ·ذ»ذ¸ر‡ذ½ر‹ذµ ذ¼ذµر‚ذ¾ذ´ر‹ ذ؟ذ¾ذ´ذ°ر‡ذ¸ رپ ذ²ر€ذ°ر‰ذµذ½ذ¸ذµذ¼ , ذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ¼ذ¾ذ³رƒر‚ ذ؟ر€ذ¸ذ²ذµرپر‚ذ¸ ذ؛ ذ·ذ½ذ°ر‡ذ¸ر‚ذµذ»رŒذ½ذ¾ذ¼رƒ ذ¾ر‚ذ؛ذ»ذ¾ذ½ذµذ½ذ¸رژ ذ¼رڈر‡ذ° ذ¾ر‚ ذ؟ذ¾ذ»رڈ .
ذ،ذ¸ذ»ر‹, ذ´ذµذ¹رپر‚ذ²رƒرژر‰ذ¸ذµ ذ½ذ° ر„رƒر‚ذ±ذ¾ذ»رŒذ½ر‹ذ¹ ذ¼رڈر‡ ذ¸ذ»ذ¸ ذ¼رڈر‡ ذ´ذ»رڈ ر€ذµذ³ذ±ذ¸ ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ, — رچر‚ذ¾ رپذ¸ذ»ذ° ر‚رڈذ¶ذµرپر‚ذ¸ , ذ½ذ¾ر€ذ¼ذ°ذ»رŒذ½ذ°رڈ رپذ¸ذ»ذ° ذ¸ رپذ¸ذ»ذ° ر‚ر€ذµذ½ذ¸رڈ . ذ¢ر€ذµذ½ذ¸ذµ ذ¾ذ±ر‹ر‡ذ½ذ¾ ذ¸ذ¼ذµذµر‚ آ«ذ؟ر€ذ¾ذ´ذ¾ذ»رŒذ½رƒرژآ» رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰رƒرژ ذ¸ذ·-ذ·ذ° رپذ؛ذ¾ر€ذ¾رپر‚ذ¸ ذ¼رڈر‡ذ° ذ¸ آ«ذ؛رƒذ²ر‹ر€ذ؛ذ°رژر‰ذµذ³ذ¾رپرڈآ» ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ, ذ° ر‚ذ°ذ؛ذ¶ذµ آ«ذ±ذ¾ذ؛ذ¾ذ²رƒرژآ» رپذ¾رپر‚ذ°ذ²ذ»رڈرژر‰رƒرژ ذ¸ذ·-ذ·ذ° ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° آ«ذ؟ذ¾ ذ¾رپذ¸آ», ذ²ر‹ذ·ذ²ذ°ذ½ذ½ذ¾ذ³ذ¾ ذ±ر€ذ¾رپذ؛ذ¾ذ¼. ذر‚رپذ؛ذ¾ذ؛ ذ¼رڈر‡ذ° ذ¾ذ²ذ°ذ»رŒذ½ذ¾ذ¹ ر„ذ¾ر€ذ¼ر‹ (ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ر‚ذµر…, ذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ¸رپذ؟ذ¾ذ»رŒذ·رƒرژر‚رپرڈ ذ² ر„رƒر‚ذ±ذ¾ذ»ذµ رپ رپذµر‚ذ؛ذ¾ذ¹ ذ¸ذ»ذ¸ ر€ذµذ³ذ±ذ¸ ) ذ² ر†ذµذ»ذ¾ذ¼ ذ³ذ¾ر€ذ°ذ·ذ´ذ¾ ذ¼ذµذ½ذµذµ ذ؟ر€ذµذ´رپذ؛ذ°ذ·رƒذµذ¼, ر‡ذµذ¼ ذ¾ر‚رپذ؛ذ¾ذ؛ رپر„ذµر€ذ¸ر‡ذµرپذ؛ذ¾ذ³ذ¾ ذ¼رڈر‡ذ°. ذ’ ذ·ذ°ذ²ذ¸رپذ¸ذ¼ذ¾رپر‚ذ¸ ذ¾ر‚ ذ؟ذ¾ذ»ذ¾ذ¶ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ ذ½ذ¾ر€ذ¼ذ°ذ»رŒذ½ذ°رڈ رپذ¸ذ»ذ° ذ¼ذ¾ذ¶ذµر‚ ذ´ذµذ¹رپر‚ذ²ذ¾ذ²ذ°ر‚رŒ ذ²ذ؟ذµر€ذµذ´ذ¸ ذ¸ذ»ذ¸ ذ؟ذ¾ذ·ذ°ذ´ذ¸ ر†ذµذ½ر‚ر€ذ° ذ¼ذ°رپرپر‹ ذ¼رڈر‡ذ°, ذ° ر‚ر€ذµذ½ذ¸ذµ ذ¾ ذ·ذµذ¼ذ»رژ ذ±رƒذ´ذµر‚ ذ·ذ°ذ²ذ¸رپذµر‚رŒ ذ¾ر‚ ذ²ر‹ر€ذ°ذ²ذ½ذ¸ذ²ذ°ذ½ذ¸رڈ ذ¼رڈر‡ذ°, ذ° ر‚ذ°ذ؛ذ¶ذµ ذ¾ر‚ ذµذ³ذ¾ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ, ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ذ¸ رپذ؛ذ¾ر€ذ¾رپر‚ذ¸ رƒذ´ذ°ر€ذ°. ذڑذ¾ذ³ذ´ذ° رپذ¸ذ»ر‹, ذ´ذµذ¹رپر‚ذ²رƒرژر‰ذ¸ذµ ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½ذ¾ ر†ذµذ½ر‚ر€ذ° ذ¼ذ°رپرپ ذ¼رڈر‡ذ°, ذ¸ذ·ذ¼ذµذ½رڈرژر‚رپرڈ ذ؟ذ¾ ذ¼ذµر€ذµ ر‚ذ¾ذ³ذ¾, ذ؛ذ°ذ؛ ذ¼رڈر‡ ذ؛ذ°ر‚ذ¸ر‚رپرڈ ذ؟ذ¾ ذ·ذµذ¼ذ»ذµ, ذ¸ ذ²رپذµ رپذ¸ذ»ر‹ ذ¼ذ¾ذ³رƒر‚ ذ¾ذ؛ذ°ذ·ر‹ذ²ذ°ر‚رŒ ذ½ذ° ذ¼رڈر‡ ذ؛ر€رƒر‚رڈر‰ذ¸ذ¹ ذ¼ذ¾ذ¼ذµذ½ر‚ , ذ²ذ؛ذ»رژر‡ذ°رڈ ذ½ذ¾ر€ذ¼ذ°ذ»رŒذ½رƒرژ رپذ¸ذ»رƒ ذ¸ رپذ¸ذ»رƒ ر‚رڈذ¶ذµرپر‚ذ¸. ذر‚ذ¾ ذ¼ذ¾ذ¶ذµر‚ ذ؟ر€ذ¸ذ²ذµرپر‚ذ¸ ذ؛ ذ¾ر‚رپذ؛ذ¾ذ؛رƒ ذ¼رڈر‡ذ° ذ²ذ؟ذµر€ر‘ذ´, ذ½ذ°ذ·ذ°ذ´ ذ¸ذ»ذ¸ ذ² رپر‚ذ¾ر€ذ¾ذ½رƒ. ذںذ¾رپذ؛ذ¾ذ»رŒذ؛رƒ ذ¼ذ¾ذ¶ذ½ذ¾ ذ؟ذµر€ذµذ´ذ°ر‚رŒ ذ½ذµذ؛ذ¾ر‚ذ¾ر€رƒرژ ر‡ذ°رپر‚رŒ ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛ذ¾ذ¹ رچذ½ذµر€ذ³ذ¸ذ¸ ذ²ر€ذ°ر‰ذµذ½ذ¸رڈ ذ² ذ؛ذ¸ذ½ذµر‚ذ¸ر‡ذµرپذ؛رƒرژ رچذ½ذµر€ذ³ذ¸رژ ذ؟ذ¾رپر‚رƒذ؟ذ°ر‚ذµذ»رŒذ½ذ¾ذ³ذ¾ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ, ذ²ذ¾ذ·ذ¼ذ¾ذ¶ذ½ذ¾ ذ´ذ°ذ¶ذµ, ر‡ر‚ذ¾ COR ذ±رƒذ´ذµر‚ ذ±ذ¾ذ»رŒرˆذµ 1 ذ¸ذ»ذ¸ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ´ذ²ذ¸ذ¶ذµذ½ذ¸رڈ ذ¼رڈر‡ذ° ذ²ذ؟ذµر€ر‘ذ´ رƒذ²ذµذ»ذ¸ر‡ذ¸ر‚رپرڈ ذ؟ر€ذ¸ رƒذ´ذ°ر€ذµ[ 35]
ذںذ¾ذ؟رƒذ»رڈر€ذ½ذ°رڈ ذ´ذµذ¼ذ¾ذ½رپر‚ر€ذ°ر†ذ¸رڈ ذ²ذ؛ذ»رژر‡ذ°ذµر‚ ذ² رپذµذ±رڈ ذ¾ر‚رپذ؛ذ¾ذ؛ ذ½ذµرپذ؛ذ¾ذ»رŒذ؛ذ¸ر… رپذ»ذ¾ذ¶ذµذ½ذ½ر‹ر… ذ¼رڈر‡ذµذ¹. ذ•رپذ»ذ¸ ر‚ذµذ½ذ½ذ¸رپذ½ر‹ذ¹ ذ¼رڈر‡ ذ؟ذ¾ذ»ذ¾ذ¶ذ¸ر‚رŒ ذ½ذ° ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ر‹ذ¹ ذ¼رڈر‡ ذ¸ ذ¾ذ±ذ° ذ¼رڈر‡ذ° رƒر€ذ¾ذ½ذ¸ر‚رŒ ذ¾ذ´ذ½ذ¾ذ²ر€ذµذ¼ذµذ½ذ½ذ¾, ر‚ذµذ½ذ½ذ¸رپذ½ر‹ذ¹ ذ¼رڈر‡ ذ؟ذ¾ذ´ذ؟ر€ر‹ذ³ذ½ذµر‚ ذ½ذ°ذ¼ذ½ذ¾ذ³ذ¾ ذ²ر‹رˆذµ, ر‡ذµذ¼ ذµرپذ»ذ¸ ذ±ر‹ ذ¾ذ½ رƒذ؟ذ°ذ» رپذ°ذ¼ ذ؟ذ¾ رپذµذ±ذµ, ذ´ذ°ذ¶ذµ ذ؟ر€ذµذ²ر‹رپذ¸ذ² رپذ²ذ¾رژ ذ؟ذµر€ذ²ذ¾ذ½ذ°ر‡ذ°ذ»رŒذ½رƒرژ ذ²ر‹رپذ¾ر‚رƒ ذ²ر‹ذ±ر€ذ¾رپذ°[ 36] [ 37] [ 38] [ 36]
ذذ±ر‹ر‡ذ½ذ¾ذµ ذ¾ذ±رٹرڈرپذ½ذµذ½ذ¸ذµ ذ؟ر€ذµذ´ذ؟ذ¾ذ»ذ°ذ³ذ°ذµر‚ ر€ذ°رپرپذ¼ذ¾ر‚ر€ذµذ½ذ¸ذµ ذ´ذ²رƒر… ذ¾ر‚ذ´ذµذ»رŒذ½ر‹ر… رƒذ´ذ°ر€ذ¾ذ²: رƒذ´ذ°ر€ذ° ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ¾ذ± ذ؟ذ¾ذ» ذ¸ رƒذ´ذ°ر€ذ° ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ¾ ر‚ذµذ½ذ½ذ¸رپذ½ر‹ذ¹ ذ¼رڈر‡[ 36] [ 37] رƒذ؟ر€رƒذ³ذ¸ذµ رپر‚ذ¾ذ»ذ؛ذ½ذ¾ذ²ذµذ½ذ¸رڈ , ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ر‹ذ¹ ذ¼رڈر‡ رƒذ´ذ°ر€رڈذµر‚رپرڈ ذ¾ذ± ذ؟ذ¾ذ» ذ؟ر€ذ¸ رپذ؛ذ¾ر€ذ¾رپر‚ذ¸ 1 ذ¼/رپ ذ¸ ذ²ذ¾رپرپر‚ذ°ذ½ذ¾ذ²ذ¸ر‚رپرڈ ذ´ذ¾ رپذ؛ذ¾ر€ذ¾رپر‚ذ¸ 1 ذ¼/رپ. ذ¢ذµذ½ذ½ذ¸رپذ½ر‹ذ¹ ذ¼رڈر‡ ذ»ذµر‚ذ¸ر‚ رپذ¾ رپذ؛ذ¾ر€ذ¾رپر‚رŒرژ 1 ذ¼/رپ ر‚ذ¾ذ³ذ´ذ° ذ±رƒذ´ذµر‚ ذ¸ذ¼ذµر‚رŒ ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½رƒرژ رپذ؛ذ¾ر€ذ¾رپر‚رŒ رƒذ´ذ°ر€ذ° 2 ذ¼/رپ, ر‡ر‚ذ¾ ذ¾ذ·ذ½ذ°ر‡ذ°ذµر‚, ر‡ر‚ذ¾ ذ¾ذ½ ذ¾ر‚رپذ؛ذ¾ر‡ذ¸ر‚ رپذ¾ رپذ؛ذ¾ر€ذ¾رپر‚رŒرژ 2 ذ¼/رپ ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½ذ¾ ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ°, ذ¸ذ»ذ¸ 3 ذ¼/رپ ذ¾ر‚ذ½ذ¾رپذ¸ر‚ذµذ»رŒذ½ذ¾ ذ؟ذ¾ذ»ذ° ذ¸ رƒر‚ر€ذ¾ذ¸ر‚ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¾ر‚رپذ؛ذ¾ذ؛ذ° ذ؟ذ¾ رپر€ذ°ذ²ذ½ذµذ½ذ¸رژ رپذ¾ رپذ؛ذ¾ر€ذ¾رپر‚رŒرژ رƒذ´ذ°ر€ذ° ذ¾ ذ؟ذ¾ذ». ذر‚ذ¾ ذ¾ذ·ذ½ذ°ر‡ذ°ذµر‚, ر‡ر‚ذ¾ ذ¼رڈر‡ ذ¾ر‚رپذ؛ذ¾ر‡ذ¸ر‚ ذ½ذ° ذ²ر‹رپذ¾ر‚رƒ, ذ² ذ´ذµذ²رڈر‚رŒ ر€ذ°ذ· ذ؟ر€ذµذ²ر‹رˆذ°رژر‰رƒرژ ذµذ³ذ¾ ذ؟ذµر€ذ²ذ¾ذ½ذ°ر‡ذ°ذ»رŒذ½رƒرژ ذ²ر‹رپذ¾ر‚رƒ[ note 2] ذ½ذµرƒذ؟ر€رƒذ³ذ¸ر… رپر‚ذ¾ذ»ذ؛ذ½ذ¾ذ²ذµذ½ذ¸ذ¹ ر‚ذµذ½ذ½ذ¸رپذ½ر‹ذ¹ ذ¼رڈر‡ رƒذ²ذµذ»ذ¸ر‡ذ¸ر‚ رپذ²ذ¾رژ رپذ؛ذ¾ر€ذ¾رپر‚رŒ ذ¸ ذ²ر‹رپذ¾ر‚رƒ ذ¾ر‚رپذ؛ذ¾ذ؛ذ° ذ² ذ¼ذµذ½رŒرˆذµذµ ر‡ذ¸رپذ»ذ¾ ر€ذ°ذ·, ذ½ذ¾ ذ²رپر‘ ر€ذ°ذ²ذ½ذ¾ ذ±رƒذ´ذµر‚ ذ؟ذ¾ذ´ذ؟ر€ر‹ذ³ذ¸ذ²ذ°ر‚رŒ ذ±ر‹رپر‚ر€ذµذµ ذ¸ ذ²ر‹رˆذµ, ر‡ذµذ¼ رپذ°ذ¼ ذ؟ذ¾ رپذµذ±ذµ[ 37]
ذ¥ذ¾ر‚رڈ ذ؟ر€ذµذ´ذ؟ذ¾ذ»ذ¾ذ¶ذµذ½ذ¸رڈ ذ¾ذ± ذ¾ر‚ذ´ذµذ»رŒذ½ر‹ر… رƒذ´ذ°ر€ذ°ر… ذ½ذ° رپذ°ذ¼ذ¾ذ¼ ذ´ذµذ»ذµ ذ½ذµذ²ذµر€ذ½ر‹ (رˆذ°ر€ر‹ ذ¾رپر‚ذ°رژر‚رپرڈ ذ² ر‚ذµرپذ½ذ¾ذ¼ ذ؛ذ¾ذ½ر‚ذ°ذ؛ر‚ذµ ذ´ر€رƒذ³ رپ ذ´ر€رƒذ³ذ¾ذ¼ ذ½ذ° ذ؟ر€ذ¾ر‚رڈذ¶ذµذ½ذ¸ذ¸ ذ±ذ¾ذ»رŒرˆذµذ¹ ر‡ذ°رپر‚ذ¸ رƒذ´ذ°ر€ذ°), رچر‚ذ° ذ¼ذ¾ذ´ذµذ»رŒ, ر‚ذµذ¼ ذ½ذµ ذ¼ذµذ½ذµذµ, ر…ذ¾ر€ذ¾رˆذ¾ ذ²ذ¾رپذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´ذ¸ر‚ رچذ؛رپذ؟ذµر€ذ¸ذ¼ذµذ½ر‚ذ°ذ»رŒذ½ر‹ذµ ر€ذµذ·رƒذ»رŒر‚ذ°ر‚ر‹[ 37] ذ؛ذ¾ذ»ذ»ذ°ذ؟رپ رڈذ´ر€ذ° رپذ²ذµر€ر…ذ½ذ¾ذ²ر‹ر… [ 36] ذ³ر€ذ°ذ²ذ¸ر‚ذ°ر†ذ¸ذ¾ذ½ذ½ر‹ر… ذ¼ذ°ذ½ر‘ذ²ر€ذ°ر… [ 39]
ذ،ذ؟ذ¾ر€ر‚ذ¸ذ²ذ½ر‹ذµ ر„ذµذ´ذµر€ذ°ر†ذ¸ذ¸ ذ½ذµذ؛ذ¾ر‚ذ¾ر€ر‹ر… ذ²ذ¸ذ´ذ¾ذ² رپذ؟ذ¾ر€ر‚ذ° ر€ذµذ³رƒذ»ذ¸ر€رƒرژر‚ رƒذ؟ر€رƒذ³ذ¾رپر‚رŒ ذ¼رڈر‡ذ° ر€ذ°ذ·ذ»ذ¸ر‡ذ½ر‹ذ¼ذ¸ رپذ؟ذ¾رپذ¾ذ±ذ°ذ¼ذ¸: ذ½ذµذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ؟ر€رڈذ¼ر‹ذ¼ذ¸, ذ½ذµذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ؛ذ¾رپذ²ذµذ½ذ½ر‹ذ¼ذ¸.
AFL : ر€ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ¼ذ°ذ½ذ¾ذ¼ذµر‚ر€ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ر„رƒر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ½ذ° رƒر€ذ¾ذ²ذ½ذµ 62 ذ؛ذںذ° ذ¸ 76 ذ؛ذںذ° [ 40] ذ¤ذکذ‘ذگ : ذ ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ¼ذ°ذ½ذ¾ذ¼ذµر‚ر€ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ, ر‡ر‚ذ¾ذ±ر‹ ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ر‹ذ¹ ذ¼رڈر‡ ذ؟ذ¾ذ´ذ؟ر€ر‹ذ³ذ¸ذ²ذ°ذ» ذ² ذ؟ر€ذµذ´ذµذ»ذ°ر… 1200 ذ¼ذ¼ ذ¸ 1400 ذ¼ذ¼ (ذ²ذµر€ر…ذ½رڈرڈ ر‡ذ°رپر‚رŒ رˆذ°ر€ذ°) ذ؟ر€ذ¸ ذ؟ذ°ذ´ذµذ½ذ¸ذ¸ رپ ذ²ر‹رپذ¾ر‚ر‹ 1800 ذ¼ذ¼ (ذ½ذ¸ذ¶ذ½رڈرڈ ر‡ذ°رپر‚رŒ رˆذ°ر€ذ°)[ 41] [ note 3] FIFA : ر€ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ¼ذ°ذ½ذ¾ذ¼ذµر‚ر€ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ر„رƒر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ² ذ؟ر€ذµذ´ذµذ»ذ°ر… 0,6 ذ¸ 1,1 ذ°ر‚ذ¼ ذ½ذ° رƒر€ذ¾ذ²ذ½ذµ ذ¼ذ¾ر€رڈ (ذ¾ر‚ 61 ذ´ذ¾ 111 ذ؛ذںذ° )[ 42] FIVB : ذ ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ¼ذ°ذ½ذ¾ذ¼ذµر‚ر€ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ذ²ذ¾ذ»ذµذ¹ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ² ذ؟ر€ذµذ´ذµذ»ذ°ر… 0,30 kgF /cm2 ذ´ذ¾ 0,325 kgF /cm2 (ذ¾ر‚ 29,4 ذ´ذ¾ 31,9 ذ؛ذںذ°) ذ´ذ»رڈ ذ²ذ¾ذ»ذµذ¹ذ±ذ¾ذ»ذ° ذ² ذ·ذ°ذ؛ر€ر‹ر‚ر‹ر… ذ؟ذ¾ذ¼ذµر‰ذµذ½ذ¸رڈر… ذ¸ 0,175 kgF /cm2 ذ´ذ¾ 0,225 kgF /cm2 (ذ¾ر‚ 17,2 ذ´ذ¾ 22,1 ذ؛ذںذ°) ذ´ذ»رڈ ذ؟ذ»رڈذ¶ذ½ذ¾ذ³ذ¾ ذ²ذ¾ذ»ذµذ¹ذ±ذ¾ذ»ذ° [ 43] [ 44] ITF : ذ ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ²ر‹رپذ¾ر‚رƒ ذ¾ر‚رپذ؛ذ¾ذ؛ذ° ر‚ذµذ½ذ½ذ¸رپذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ؟ر€ذ¸ ذ؟ذ°ذ´ذµذ½ذ¸ذ¸ ذ½ذ° آ«ذ³ذ»ذ°ذ´ذ؛ذ¸ذ¹, ذ¶ر‘رپر‚ذ؛ذ¸ذ¹ ذ¸ ذ³ذ¾ر€ذ¸ذ·ذ¾ذ½ر‚ذ°ذ»رŒذ½ر‹ذ¹ ذ±ذ»ذ¾ذ؛ ذ±ذ¾ذ»رŒرˆذ¾ذ¹ ذ¼ذ°رپرپر‹آ». ذ”ذ»رڈ ر€ذ°ذ·ذ½ر‹ر… ر‚ذ¸ذ؟ذ¾ذ² ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚ذµذ¹ ر€ذ°ذ·ر€ذµرˆذµذ½ر‹ ر€ذ°ذ·ذ½ر‹ذµ ر‚ذ¸ذ؟ر‹ ذ¼رڈر‡ذµذ¹. ذںر€ذ¸ ذ؟ذ°ذ´ذµذ½ذ¸ذ¸ رپ ذ²ر‹رپذ¾ر‚ر‹ 100 ذ´رژذ¹ذ¼ذ¾ذ² (254 رپذ¼), ذ¾ر‚رپذ؛ذ¾ذ؛ ذ´ذ¾ذ»ذ¶ذµذ½ رپذ¾رپر‚ذ°ذ²ذ»رڈر‚رŒ ذ¨ذ°ذ±ذ»ذ¾ذ½:Convert/– ذ´ذ»رڈ رˆذ°ر€ذ¾ذ² ر‚ذ¸ذ؟ذ° 1 — ذ¨ذ°ذ±ذ»ذ¾ذ½:Convert/– ذ´ذ»رڈ رˆذ°ر€ذ¾ذ² ر‚ذ¸ذ؟ذ° 2 ذ¸ ر‚ذ¸ذ؟ذ° 3 ذ¸ ذ¨ذ°ذ±ذ»ذ¾ذ½:Convert/– ذ´ذ»رڈ ذ²ر‹رپذ¾ر‚ذ½ر‹ر… ذ¼رڈر‡ذµذ¹[ 45] [ note 3] ITTF : ر€ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ¸ذ³ر€ذ¾ذ²رƒرژ ذ؟ذ¾ذ²ذµر€ر…ذ½ذ¾رپر‚رŒ ر‚ذ°ذ؛, ر‡ر‚ذ¾ذ±ر‹ ذ¼رڈر‡ ذ´ذ»رڈ ذ½ذ°رپر‚ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ر‚ذµذ½ذ½ذ¸رپذ° ذ؟ذ¾ذ´ذ؟ر€ر‹ذ³ذ¸ذ²ذ°ذ» ذ؟ر€ذ¸ذ¼ذµر€ذ½ذ¾ ذ½ذ° 23 رپذ¼ ذ؟ر€ذ¸ ذ؟ذ°ذ´ذµذ½ذ¸ذ¸ رپ ذ²ر‹رپذ¾ر‚ر‹ 30 رپذ¼[ 46] [ note 3] ذذ‘ذگ : ر€ذµذ³رƒذ»ذ¸ر€رƒذµر‚ ذ¼ذ°ذ½ذ¾ذ¼ذµر‚ر€ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ذ±ذ°رپذ؛ذµر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ² ذ؟ر€ذµذ´ذµذ»ذ°ر… ذ¾ر‚ 7,5 ذ´ذ¾ 8,5 ر„رƒذ½ر‚ذ¾ذ² ذ½ذ° ذ؛ذ²ذ°ذ´ر€ذ°ر‚ذ½ر‹ذ¹ ذ´رژذ¹ذ¼ (ذ¾ر‚ 51,7 ذ´ذ¾ 58,6 ذ؛ذںذ°)[ 47] ذذ¤ذ› : ذœذ°ذ½ذ¾ذ¼ذµر‚ر€ذ¸ر‡ذµرپذ؛ذ¾ذµ ذ´ذ°ذ²ذ»ذµذ½ذ¸ذµ ذ² ذ°ذ¼ذµر€ذ¸ذ؛ذ°ذ½رپذ؛ذ¾ذ¼ ر„رƒر‚ذ±ذ¾ذ»ذµ ر€ذµذ³رƒذ»ذ¸ر€رƒذµر‚رپرڈ ذ² ذ´ذ¸ذ°ذ؟ذ°ذ·ذ¾ذ½ذµ ذ¾ر‚ 12,5 ذ´ذ¾ 13,5 ر„رƒذ½ر‚ذ¾ذ² ذ½ذ° ذ؛ذ²ذ°ذ´ر€ذ°ر‚ذ½ر‹ذ¹ ذ´رژذ¹ذ¼ (ذ¾ر‚ 86 ذ´ذ¾ 93 ذ؛ذںذ°)[ 48] R&A /USGA : ذ½ذ°ذ؟ر€رڈذ¼رƒرژ ذ¾ذ³ر€ذ°ذ½ذ¸ر‡ذ¸ذ²ذ°ذµر‚ COR ذ¼رڈر‡ذ° ذ´ذ»رڈ ذ³ذ¾ذ»رŒر„ذ° , ذ؛ذ¾ر‚ذ¾ر€ر‹ذ¹ ذ½ذµ ذ´ذ¾ذ»ذ¶ذµذ½ ذ؟ر€ذµذ²ر‹رˆذ°ر‚رŒ 0,83 ذ؟ذ¾ ذ¾ر‚ذ½ذ¾رˆذµذ½ذ¸رژ ذ؛ ذ؛ذ»رژرˆذ؛ذµ ذ´ذ»رڈ ذ³ذ¾ذ»رŒر„ذ° [ 49] ذ”ذ°ذ²ذ»ذµذ½ذ¸ذµ ذ°ذ¼ذµر€ذ¸ذ؛ذ°ذ½رپذ؛ذ¾ذ³ذ¾ ر„رƒر‚ذ±ذ¾ذ»رŒذ½ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ±ر‹ذ»ذ¾ ذ² ر†ذµذ½ر‚ر€ذµ رپذ؟ذ¾ر€ذ° ذ¾ ذ´ذµر„ذ»ذ°ر‚ذ³ذ°ر‚ذµ [ 50] [ 51] ذ±ذµذ¹رپذ±ذ¾ذ»ذµ ذ؟ذ¾رڈذ²ذ»ذµذ½ذ¸ذµ ذ¼رڈر‡ذ° ذ½ذ° ذ¾رپذ½ذ¾ذ²ذµ ذ؟ر€ذ¾ذ±ذ؛ذ¸ ذ؟ذ¾ذ¼ذ¾ذ³ذ»ذ¾ ذ؟ذ¾ذ»ذ¾ذ¶ذ¸ر‚رŒ ذ؛ذ¾ذ½ذµر† رچذ؟ذ¾ر…ذµ ذ¼ر‘ر€ر‚ذ²ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° ذ¸ ذ؟ذ¾ذ»ذ¾ذ¶ذ¸ر‚رŒ ذ½ذ°ر‡ذ°ذ»ذ¾ رچذ؟ذ¾ر…ذµ ذ¶ذ¸ذ²ذ¾ذ³ذ¾ ذ¼رڈر‡ذ° [ 52] [ 53]
ذڑذ¾ذ¼ذ¼ذµذ½ر‚ذ°ر€ذ¸ذ¸
↑ ذ—ذ´ذµرپرŒ v ذ¸ u — رچر‚ذ¾ ذ½ذµ ر‚ذ¾ذ»رŒذ؛ذ¾ ذ²ذµذ»ذ¸ر‡ذ¸ذ½ذ° رپذ؛ذ¾ر€ذ¾رپر‚ذµذ¹, ذ½ذ¾ ذ¸ ذ¸ر… ذ½ذ°ذ؟ر€ذ°ذ²ذ»ذµذ½ذ¸ذµ (ذ·ذ½ذ°ذ؛).
↑ ذںذ¾رپذ؛ذ¾ذ»رŒذ؛رƒ رپذ¾ر…ر€ذ°ذ½ذµذ½ذ¸ذµ ذ¼ذµر…ذ°ذ½ذ¸ر‡ذµرپذ؛ذ¾ذ¹ رچذ½ذµر€ذ³ذ¸ذ¸ ذ؟ذ¾ذ´ر€ذ°ذ·رƒذ¼ذµذ²ذ°ذµر‚
1
2
m
v
f
2
=
m
g
H
f
{\displaystyle \textstyle {\frac {1}{2}}mv_{\text{f}}^{2}=mgH_{\text{f}}}
H
f
{\displaystyle \textstyle H_{\text{f}}}
v
f
2
{\displaystyle v_{\text{f}}^{2}}
↑ 1 2 3 ذ ذ°رپرپر‡ذ¸ر‚ذ°ذ½ذ¾ رپ ذ¸رپذ؟ذ¾ذ»رŒذ·ذ¾ذ²ذ°ذ½ذ¸ذµذ¼
e
=
H
f
H
i
{\displaystyle \textstyle e={\sqrt {\frac {H_{\text{f}}}{H_{\text{i}}}}}}
ذکرپر‚ذ¾ر‡ذ½ذ¸ذ؛ذ¸
↑
The Sport of Life and Death: The Mesoamerican Ballgame . — Thames & Hudson , 2001. — ISBN 0-500-05108-9 .
↑ 1 2
Brancazio, P. J. (1985). "Trajectory of a fly ball" . The Physics Teacher 23 (1): 20—23. Bibcode :1985PhTea..23...20B . doi :10.1119/1.2341702 .
↑
Walker, J. Fundamentals of Physics . — 10th Extended. — John Wiley & Sons , 2014. — ISBN 978-1-118-23072-5 .
↑ 1 2
Bush, J. W. M. The aerodynamics of the beautiful game // Sports Physics. — Les أ‰ditions de l'أ‰cole Polytechnique , 2013. — P. 171. — ISBN 978-2-7302-1615-9 .
↑
Hirt, C.; Claessens, S.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. (2013). "New ultrahigh-resolution picture of Earth's gravity field" . Geophysical Research Letters 40 (16): 4279—4283. Bibcode :2013GeoRL..40.4279H . doi :10.1002/grl.50838
↑ 1 2 Nave, R. Trajectories (ذ½ذµذ¾ذ؟ر€.) . HyperPhysics ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 18 ذ¸رژذ»رڈ 2019 ذ³ذ¾ذ´ذ°.↑ Dry air properties (ذ½ذµذ¾ذ؟ر€.) . The Engineering Toolbox ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 25 ذ¼ذ°ر€ر‚ذ° 2017 ذ³ذ¾ذ´ذ°.↑
Southard, J. Chapter 3: Flow past a sphere II: Stoke's law, the Bernoulli equation, turbulence, boundary layers, flow separation // Special Topics: An Introduction to Fluid Motions, Sediment Transport, and Current-generated Sedimentary Structures. — MIT , Fall 2006. — P. 35–82.
↑
Metha, R. D. Sports ball aerodynamics // Sport Aerodynamics. — Springer , 2008. — Vol. 506. — P. 229–331. — ISBN 978-3-211-89296-1 . — doi :10.1007/978-3-211-89297-8_12 .
↑ Drag of a sphere (ذ½ذµذ¾ذ؟ر€.) . NASA . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 28 ذ¼ذ°رڈ 2019 ذ³ذ¾ذ´ذ°.↑ Ideal lift of a spinning ball (ذ½ذµذ¾ذ؟ر€.) . NASA . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 2 ر„ذµذ²ر€ذ°ذ»رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 4 رپذµذ½ر‚رڈذ±ر€رڈ 2018 ذ³ذ¾ذ´ذ°.↑ 1 2 Nathan, A. M. (2008). "The effect of spin on the flight of a baseball" (PDF) . American Journal of Physics 76 (2): 119—124. arXiv :physics/0605041 Bibcode :2008AmJPh..76..119N . doi :10.1119/1.2805242 . S2CID 15494386 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 26 ذ¼ذ°رڈ 2019 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ Kim, J.; Park, H.; Choi, H.; Yoo, J. Y. (2011). "Inverse Magnus effect on a rotating sphere" (PDF) . 64th Annual Meeting of the APS Division of Fluid Dynamics . American Physical Society . Bibcode :2011APS..DFD.A7008K . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 1 ذ°ذ²ذ³رƒرپر‚ذ° 2023 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑
Kim, J.; Choi, H.; Park, H.; Yoo, J. Y. (2014). "Inverse Magnus effect on a rotating sphere: When and why". Journal of Fluid Mechanics 754 : R2. Bibcode :2014JFM...754R...2K . doi :10.1017/jfm.2014.428 . S2CID 122453684 .
↑ Magnus effect (ذ½ذµذ¾ذ؟ر€.) . HumanKinetics.com (11 ذ½ذ¾رڈذ±ر€رڈ 2008). ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 27 رڈذ½ذ²ذ°ر€رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ ذ¸ذ· ذ¾ر€ذ¸ذ³ذ¸ذ½ذ°ذ»ذ° 28 ذ´ذµذ؛ذ°ذ±ر€رڈ 2018 ذ³ذ¾ذ´ذ°.↑ DeForest, C. Why are golf balls dimpled? (ذ½ذµذ¾ذ؟ر€.) The Original Usenet Physics FAQ (1997). ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 27 رڈذ½ذ²ذ°ر€رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ ذ¸ذ· ذ¾ر€ذ¸ذ³ذ¸ذ½ذ°ذ»ذ° 23 ذ¸رژذ»رڈ 2019 ذ³ذ¾ذ´ذ°.↑ Clanet, C. (2015). "Sports ballistics" (PDF) . Annual Review of Fluid Mechanics 47 : 455—478. Bibcode :2015AnRFM..47..455C . doi :10.1146/annurev-fluid-010313-141255 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 29 ذ¼ذ°ر€ر‚ذ° 2017 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ Inzamam charged by ICC (ذ½ذµذ¾ذ؟ر€.) . The Guardian ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 18 ذ½ذ¾رڈذ±ر€رڈ 2018 ذ³ذ¾ذ´ذ°.↑
Okrent, D. Baseball anecdotes / D. Okrent, S. Wulf. — Oxford University Press , 1989. — P. 89. — ISBN 978-0-19-504396-9 .
↑ 1 2
Post, S. Applied and computational fluid mechanics . — Jones and Bartlett Publishers , 2010. — P. 280–282. — ISBN 978-1-934015-47-6 .
↑ 1 2 Cross, R. (1999). "The bounce of a ball" (PDF) . American Journal of Physics 67 (3): 222—227. Bibcode :1999AmJPh..67..222C . doi :10.1119/1.19229 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 23 ذ´ذµذ؛ذ°ذ±ر€رڈ 2018 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ 1 2 3 4 5 6 7
Georgallas, A.; Landry, G. (2016). "The coefficient of restitution of pressurized balls: A mechanistic model" . Canadian Journal of Physics 94 (1): 42. Bibcode :2016CaJPh..94...42G . doi :10.1139/cjp-2015-0378 . hdl :1807/69855
↑
Coefficient of restitution (ذ½ذµذ¾ذ؟ر€.) . RacquetResearch.com . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 27 رڈذ½ذ²ذ°ر€رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ ذ¸ذ· ذ¾ر€ذ¸ذ³ذ¸ذ½ذ°ذ»ذ° 23 ذ½ذ¾رڈذ±ر€رڈ 2016 ذ³ذ¾ذ´ذ°.
↑
Cross, R.; Nathan, A. M. (2006). "Scattering of a baseball by a bat". American Journal of Physics 74 (10): 896—904. arXiv :physics/0605040 Bibcode :2006AmJPh..74..896C . doi :10.1119/1.2209246 . S2CID 15488042 .
↑ 1 2
Haron, A.; Ismail, K. A. (2012). "Coefficient of restitution of sports balls: A normal drop test" . IOP Conference Series: Materials Science and Engineering 36 (1): 012038. Bibcode :2012MS&E...36a2038H . doi :10.1088/1757-899X/36/1/012038
↑ 1 2 Cross, R. (2000). "The coefficient of restitution for collisions of happy balls, unhappy balls, and tennis balls" (PDF) . American Journal of Physics 68 (11): 1025—1031. Bibcode :2000AmJPh..68.1025C . doi :10.1119/1.1285945 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 22 ذ´ذµذ؛ذ°ذ±ر€رڈ 2018 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ Cross, R. (2002). "Grip-slip behavior of a bouncing ball" (PDF) . American Journal of Physics 70 (11): 1093—1102. Bibcode :2002AmJPh..70.1093C . doi :10.1119/1.1507792 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 22 ذ´ذµذ؛ذ°ذ±ر€رڈ 2018 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ 1 2
Zhang, X.; Vu-Quoc, L. (2002). "Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisions". International Journal of Impact Engineering 27 (3): 317—341. doi :10.1016/S0734-743X(01)00052-5 .
↑ Hesser-Knoll, M. Ball spin during bounce (ذ½ذµذ¾ذ؟ر€.) . The Physics of Tennis . University of Alaska Fairbanks (2014). ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 1 ر„ذµذ²ر€ذ°ذ»رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 2 رڈذ½ذ²ذ°ر€رڈ 2019 ذ³ذ¾ذ´ذ°.↑ Lindsey, C. Follow the bouncing ball (ذ½ذµذ¾ذ؟ر€.) . Tennis Industry (ذ°ذ؟ر€ذµذ»رŒ 2004). ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 1 ر„ذµذ²ر€ذ°ذ»رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 20 ذ½ذ¾رڈذ±ر€رڈ 2018 ذ³ذ¾ذ´ذ°.↑
Allen, T.; Haake, S.; Goodwill, S. (2010). "Effect of friction on tennis ball impacts". Proceedings of the Institution of Mechanical Engineers, Part P 224 (3): 229—236. doi :10.1243/17543371JSET66 .
↑ 1 2 3 Cross, R. (2005). "Bounce of a spinning ball near normal incidence" (PDF) . American Journal of Physics 73 (10): 914—920. Bibcode :2005AmJPh..73..914C . doi :10.1119/1.2008299 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 21 رپذµذ½ر‚رڈذ±ر€رڈ 2018 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑
Allen, T. (2012). "The ball's in your court" (PDF) . ANSYS Advantage ذ¾ر€ذ¸ذ³ذ¸ذ½ذ°ذ»ذ° (PDF) 5 ر„ذµذ²ر€ذ°ذ»رڈ 2017 .
↑ Jafri, S. M. M. (2004). Modeling of impact dynamics of a tennis ball with a flat surface (PDF) (Thesis). Texas A&M University . hdl :1969.1/2441 ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 22 رپذµذ½ر‚رڈذ±ر€رڈ 2017 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ Cross, R. (2011). "Bounce of an oval shaped football" (PDF) . Sports Technology 3 (3): 168—180. doi :10.1080/19346182.2011.564283 . S2CID 108409393 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 24 ذ¼ذ°ر€ر‚ذ° 2019 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ 1 2 3 4 Huebner, J. S.; Smith, T. L. (1992). "Multi-ball collisions" . The Physics Teacher 30 (1): 46. Bibcode :1992PhTea..30...46H . doi :10.1119/1.2343467 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 26 رڈذ½ذ²ذ°ر€رڈ 2020 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ 1 2 3 4 Cross, R. (2007). "Vertical bounce of two vertically aligned balls" (PDF) . American Journal of Physics 75 (11): 1009—1016. Bibcode :2007AmJPh..75.1009C . doi :10.1119/1.2772286 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 22 ذ¼ذ°ر€ر‚ذ° 2019 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ Harter, W. G. (1971). "Velocity amplification in collision experiments involving superballs" (PDF) . American Journal of Physics 39 (6): 656—663. Bibcode :1971AmJPh..39..656H . doi :10.1119/1.1986253 . ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ (PDF) 10 ذ½ذ¾رڈذ±ر€رڈ 2016 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 21 رپذµذ½ر‚رڈذ±ر€رڈ 2023 . ↑ Nave, R. Double ball drop (ذ½ذµذ¾ذ؟ر€.) . HyperPhysics ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 5 ذ¸رژذ½رڈ 2019 ذ³ذ¾ذ´ذ°.↑ Laws of Australian Football 2017 . — AFL , 2017. — P. 15.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 5 ذ¼ذ°ر€ر‚ذ° 2019 ذ½ذ° Wayback Machine ↑ Official Basketball Rules 2014 Basketball Equipment . — FIBA , 2014. — P. 12.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 15 ر„ذµذ²ر€ذ°ذ»رڈ 2017 ذ½ذ° Wayback Machine ↑ Laws of the Game: 2014–15 . — FIFA , 2014. — P. 15.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 15 ر„ذµذ²ر€ذ°ذ»رڈ 2017 ذ½ذ° Wayback Machine ↑ Official Volleyball Rules: 2017–2020 . — FIVB , 2016. — P. 16.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 12 ذ°ذ؟ر€ذµذ»رڈ 2019 ذ½ذ° Wayback Machine ↑ Official Beach Volleyball Rules: 2017–2020 . — FIVB , 2017. — P. 15.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 27 ذ°ذ²ذ³رƒرپر‚ذ° 2018 ذ½ذ° Wayback Machine ↑ ITF Approved Tennis Balls, Classified Surfaces & Recognized Courts . — ITF , 2016. — P. 4–5.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 26 ر„ذµذ²ر€ذ°ذ»رڈ 2017 ذ½ذ° Wayback Machine ↑ The International Table Tennis Federation Handbook . — ITTF , 2017. — P. 24.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 24 ذ°ذ؟ر€ذµذ»رڈ 2018 ذ½ذ° Wayback Machine ↑ Official Rules of the National Basketball Association: 2013–2014 . — NBA , 2013. — P. 10.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 20 ذ¼ذ°ر€ر‚ذ° 2019 ذ½ذ° Wayback Machine ↑ Official Playing Rules of the National Football League . — NFL , 2016. — P. 3.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 18 رپذµذ½ر‚رڈذ±ر€رڈ 2017 ذ½ذ° Wayback Machine ↑ Rubenstein, L. (2002-05-11). "Getting to COR of game, finally" . The Globe and Mail ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 17 ذ´ذµذ؛ذ°ذ±ر€رڈ 2019 . ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 27 رڈذ½ذ²ذ°ر€رڈ 2017 . ↑ Botelho, G.; Castillo, M. 'Deflategate:' 4-game suspension for Tom Brady (ذ½ذµذ¾ذ؟ر€.) . CNN (11 ذ¼ذ°رڈ 2015). ذ”ذ°ر‚ذ° ذ¾ذ±ر€ذ°ر‰ذµذ½ذ¸رڈ: 27 رڈذ½ذ²ذ°ر€رڈ 2017. ذگر€ر…ذ¸ذ²ذ¸ر€ذ¾ذ²ذ°ذ½ذ¾ 5 ر„ذµذ²ر€ذ°ذ»رڈ 2017 ذ³ذ¾ذ´ذ°.↑ Well, Jr., T. V. Investigative Report Concerning Footballs Used During the AFC Championship Game on January 18, 2015 / T. V. Well, Jr., B. S. Karp, L. L. Reisner. — Paul, Weiss, Rifkind, Wharton & Garrison LLP , 2015.ذگر€ر…ذ¸ذ²ذ½ذ°رڈ ذ؛ذ¾ذ؟ذ¸رڈ ذ¾ر‚ 7 ذ½ذ¾رڈذ±ر€رڈ 2019 ذ½ذ° Wayback Machine ↑
"Evolution of the ball" Baseball Digest
↑
Sowell, T. Dead ball vs lively ball // The Thomas Sowell Reader. — Basic Books , 2011. — ISBN 9780465022502 .