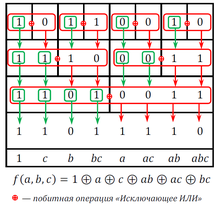
Полином Жегалкина
|
Read other articles:

Artikel ini bukan mengenai Stasiun Butuh. Stasiun Buluh Buluh Bekas bangunan dan peron stasiun BuluhNama lainStasiun Bulu, Sei Buluh, Sungai BuluhLokasiSei Buluh, Teluk Mengkudu, Serdang Bedagai, Sumatera UtaraIndonesiaOperatorKereta Api IndonesiaDivisi Regional I Sumatera Utara dan AcehLetak dari pangkalkm 50+282 lintas Medan–Tebing Tinggi[1]Jumlah peron1 peron sisiJumlah jalur1Informasi lainKode stasiunBUL9309[2]KlasifikasiIII/kecil[2]SejarahDibuka1902Ditutup1970-a...

Revista Semana País Colombia Idioma EspañolCategoría ActualidadFundación 1982Fundador Felipe López CaballeroDesarrolloDirectora Vicky DávilaPublicador Publicaciones Semana S.A.Compañía Gilinski GroupCirculaciónFrecuencia SemanalISSN 0124-5473OCLC 7475329Página web oficial[editar datos en Wikidata] Semana es una revista impresa, medio de opinión y comunicación colombiano de tendencia conservadora y de derecha populista.[1] Fue fundada en 1946 por el político y exp...

Provincia CosteraCoast ProvinceMkoa wa Pwani Provincia Coordenadas 3°00′S 39°30′E / -3, 39.5Capital MombasaEntidad Provincia • País KeniaSubdivisiones 7 distritosSuperficie • Total 84113 km²Población (2007) • Total 3 035 000 hab. • Densidad 36,08 hab/km²Huso horario UTC +3[editar datos en Wikidata] La Provincia Costera (en kiswahili: Mkoa wa Pwani) fue una de las ocho provincias en las cual...

الدوري البرتغالي الممتاز 1996-97 تفاصيل الموسم الدوري البرتغالي النسخة 59 البلد البرتغال المنظم اتحاد البرتغال لكرة القدم البطل نادي بورتو مباريات ملعوبة 306 عدد المشاركين 18 الدوري البرتغالي الممتاز 1995-96 الدوري البرتغالي الممتاز 1997-98 تعديل مصدري...

Single-pulse radar system This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Monopulse radar – news · newspapers · books · scholar · JSTOR (March 2022) (Learn how and when to remove this template message) Monopulse radar is a radar system that uses additional encoding of the radio signal to provide accurate dir...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2018) جولان-1000 النوع قاذفة صواريخ متعددة بلد الأصل سوريا تاريخ الاستخدام فترة الاستخدام 2018 - إلى الآن المستخدمون سوريا: القوات البرية العربية السورية الحروب ا

MF Norwegian School of Theology, Religion and SocietyMF vitenskapelig høyskole for teologi, religion og samfunnMottoIn Principio Erat VerbumTypePrivateEstablished1907RectorVidar L. HaanesAdministrative staff500Students1,300LocationOslo, NorwayAffiliationsThe Norwegian Association of Higher Education Institutions; IMHE; the Nordic University AssociationWebsitemf.no MF Norwegian School of Theology, Religion and Society (Norwegian: MF vitenskapelig høyskole for teologi, religion og samfunn), f...

1960–1996 civil war in Guatemala Guatemalan Civil WarPart of the Central American crisis and Cold WarIxil people carrying their loved ones' remains after an exhumation in the Ixil Triangle in February 2012.Date13 November 1960 – 29 December 1996(36 years, 1 month, 2 weeks and 2 days)LocationGuatemalaResult Peace accord signed in 1996Territorialchanges Guatemala border Franja Transversal del Norte[8]Belligerents Government of Guatemala and Guatemalan military Go...

فيكتور روزن معلومات شخصية الميلاد 5 مارس 1849(1849-03-05)تالين الوفاة 23 يناير 1908 (58 سنة)سانت بطرسبرغ مواطنة الإمبراطورية الروسية عضو في الأكاديمية الروسية للعلوم، وأكاديمية سانت بطرسبرغ للعلوم [لغات أخرى]، والأكاديمية الملكية الهولندية للفنون والعلوم إخوة...

1997 video gameThe X-FoolsMacintosh Cover artDeveloper(s)Parroty InteractivePublisher(s)Palladium InteractiveDirector(s)Steven HorowitzProducer(s)Stacey RubinProgrammer(s)WayForwardWriter(s)Tony CaminIan DeitchmanJ. P. ManouxKristin RuskBrian PosehnPatton OswaltComposer(s)Chronic MusicPlatform(s)Windows, MacintoshReleaseOctober 1, 1997[1]Genre(s)ActionMode(s)Single-player The X-Fools: The Spoof Is Out There is an interactive comedic 1997 video game developed by Parroty Interactive. It...

Wright's BiscuitsFounded1790 (public company in 1936)Defunct1973HeadquartersSouth Shields, Tyne and WearArea servedUnited Kingdom Wright's Biscuits (also Wright's (South Shields)) were established in 1790 by L Wright & Son. In the 1930s they implemented intensive factory methods for production and became a national supplier of biscuits, cakes and groceries as well as a leading employer for Tyne and Wear. Children's illustrator Mabel Lucie Attwell created the Wright's logo, a curly-haired ...

This article is about the video game series. For the first game in the series, see Double Dragon (video game). For other uses, see Double Dragon (disambiguation). Video game series Video game seriesDouble DragoniOS/Android version logoGenre(s)Beat-'em-upDeveloper(s)Technōs JapanWayForward TechnologiesArc System WorksSecret BasePublisher(s)Technōs JapanTaitoSNKMillion Corp.AtlusArc System WorksModus GamesCreator(s)Yoshihisa KishimotoPlatform(s)Arcade, NES, Master System, Atari 2600, Atari 78...

Painting by Pietro Perugino PietàArtistPietro PeruginoYearc. 1483–1493MediumOil on panelDimensions168 cm × 176 cm (66 in × 69 in)LocationUffizi Gallery, Florence Pietà is a painting by the Italian Renaissance artist Pietro Perugino, executed around 1483-1493, and housed in the Uffizi Gallery, Florence. History Detail of Mary's face. The work was painted for the church of the convent of San Giusto alle mura together with the Agony in the Ga...

Outdoor advertising company Outfront Media, Inc.TypePublicTraded asNYSE: OUTRussell 1000 ComponentS&P 600 ComponentIndustryOutdoor AdvertisingFounded1938; 85 years ago (1938)Headquarters405 Lexington Avenue, New York, NY, U.S.Area servedAmericasKey peopleJeremy J. Male (CEO)Matthew Siegel (CFO)ProductsBillboards, Transit AdvertisingRevenue US$ 2.5B (2020)[1]Number of employees2,370 (2020)[2]Websitewww.outfront.com Outfront Media billboard in Times Sq...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (June 2021) TV series or program Al-RawiالراويGenrechildren's animated historicalWritten byMohamed Kamal Hassan Mustafa ZayedDirected bySameh MostafaOriginal languageArabicNo. of seasons1No. of episodes30ProductionProduction companiesActProQuinced Al-Rawi (Arabic: الراوي, lit. “The Narrator”) is an Egyptian animated seri...

Japanese mathematician This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (June 2021) This article needs additional citations for verification. Please help improve this article by adding citations to...

Georgian pan-fried chicken dish Chicken tabakaPlace of originGeorgiaRegion or stateCaucasus, Eastern Europe, Central Asia Media: Chicken tabaka Georgian cuisine ქართული სამზარეულო Dishes & sauces Georgian bread Georgian cheese Abkhazian cheese Ajapsandali Badrijani Chakapuli Chakhokhbili Chanakhi Chashushuli Chicken tabaka Chikhirtma Chkmeruli Churchkhela Gozinaki Ispanakhi Matsvnit Khachapuri Kharcho Khashi Khinkali Kubdari Kuchmachi Kupati Lob...

American skateboard company Element SkateboardsTypeSubsidiaryIndustryRetailFounded1992FoundersJohnny Schillereff[1][2]HeadquartersIrvine, California, United StatesArea servedWorldwideProductsSkateboardsParentBoardriders, Inc.Websiteelementbrand.com Element Skateboards is an American skateboard company, founded in 1992 by Johnny Schillereff,[3] that manufactures skateboard decks, apparel, and footwear. In 2014, Element created and moved to The Branch, a creative space i...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Wah – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this template message) University of Wah واہ یونیورسٹیMottoCompetence through ExcellenceTypePrivateEstablished2005ChancellorGovernor of the ...

Mystical beings in Hinduism and Jainism This article is about the concept in Hinduism and Jainism. For esoteric knowledge holder in Buddhism, see Vidyadhara (Buddhism). A Vidyadhara couple. Sondani, circa 525 CE. Vidyadhara(s) (Sanskrit Vidyādhara, meaning wisdom-holders) are a group of supernatural beings in Indian religions who possess magical powers.[1] In Hinduism, they also attend Shiva, who lives in the Himalayas.[2] They are considered Upadevas, or demi-gods.[3]...