М-теория
|
Read other articles:

غراند غيندارمي صورة من غراند غيندارمي الموقع سويسرا المنطقة فاليه إحداثيات 46°06′26″N 7°42′43″E / 46.107222222222°N 7.7118888888889°E / 46.107222222222; 7.7118888888889 الارتفاع 4,331 متر (14,209 قدم) السلسلة جبال الألب بينيني النتوء 71 متر (233 قدم) القمة الأم فيشورن قائمة قائمة جبال سويسرا...

اضغط هنا للاطلاع على كيفية قراءة التصنيف أنبوبيات الأسنانالعصر: 20–0 مليون سنة قك ك أ س د ف بر ث ج ط ب ن الميوسيني المبكر حتى الآن[1] خنزير الأرض المرتبة التصنيفية فصيلة[2][3] التصنيف العلمي فوق النطاق حيويات مملكة عليا حقيقيات النوى مملكة&...

Caucus of the U.S. Libertarian Party Not to be confused with the Mises Institute or Ludwig von Mises. Some of this article's listed sources may not be reliable. Please help this article by looking for better, more reliable sources. Unreliable citations may be challenged or deleted. (July 2022) (Learn how and when to remove this template message) Mises CaucusLibertarian Party Mises CaucusAbbreviationLPMC[1]Named afterLudwig von MisesFormation2017FounderMichael HeiseTypeParty caucusRegi...
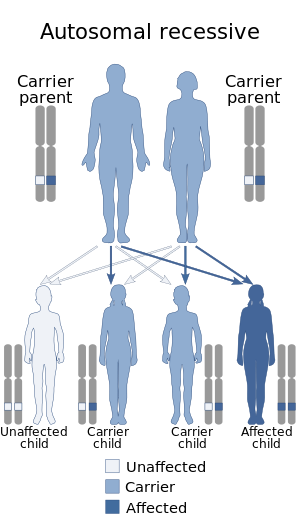
Medical conditionCerebrotendinous xanthomatosisOther namescerebrotendineous xanthomatosisCerebrotendineous xanthomatosis has an autosomal recessive pattern of inheritance.SpecialtyMedical genetics, endocrinology Cerebrotendinous xanthomatosis, also called cerebral cholesterosis,[1] is an autosomal recessive form of xanthomatosis.[2][3] It falls within a group of genetic disorders called the leukodystrophies. Presentation An inherited disorder associated with the ...

2010 single by KelisAcapellaSingle by Kelisfrom the album Flesh Tone ReleasedFebruary 20, 2010GenreElectro house[1]Length6:56 (extended mix)Label will.i.am Interscope Songwriter(s) Kelis Rogers David Guetta Fred Riesterer Jean Baptiste Makeba Riddick Producer(s)David GuettaKelis singles chronology Lil Star (2007) Acapella (2010) 4th of July (Fireworks) (2010) Acapella is a song by American singer Kelis from her fifth studio album, Flesh Tone (2010). The song is a departure from her pa...

Mallet-Lokomotive von der Bahnstrecke Igney-Avricourt–Cirey, gelistet in der Base Palissy[1] Die Base Palissy (deutsch „Palissy-Datenbank“) ist eine Datenbank des französischen Kulturministeriums, die bewegliche Kulturgüter in Frankreich, zum Beispiel Möbel, Gemälde und Kirchenschätze, aber auch Dampflokomotiven, auflistet. Der Name der Datenbank rührt von Bernard Palissy, einem Emaillekünstler des 16. Jahrhunderts, her. Die ortsfesten Kulturdenkmäler listet die Bas...

Битва під Заславом Хмельниччина Дата: травень 1649 Місце: місто Заслав Результат: перемога Речі Посполитої Сторони Річ Посполита Гетьманщина Командувачі Анджей Фірлей Іван Донець У Вікіпедії є статті про інші значення цього терміна: Битва під Заславом (значення). Битва пі�...

2014 single by Dallas SmithA Girl Like YouA Girl Like You cover with promotional caption new single at radio nowSingle by Dallas Smithfrom the album Tippin' Point ReleasedJune 23, 2014 (2014-06-23)GenreCountry popLength3:14Label604Republic NashvilleSongwriter(s)Jaren JohnstonJimmy RobbinsProducer(s)Joey MoiDallas Smith singles chronology Slow Rollin' (2014) A Girl Like You (2014) Wastin' Gas (2014) A Girl Like You' is a song written by Jaren Johnston and Jimmy Robbins, and reco...

For other uses, see PMR (disambiguation). Medical conditionPolymyalgia rheumaticaIn polmyalgia rheumatica, pain is usually located in the shoulders and hips.SpecialtyRheumatologySymptomsShoulder, neck and hip pain[1]Usual onsetAge greater than 50Diagnostic methodElevated inflammatory markers, CRP and ESRDifferential diagnosisMyositis, giant cell arteritisMedicationCorticosteroids Polymyalgia rheumatica (PMR) is a syndrome experienced as pain or stiffness, usually in the neck, shoulder...

Unjuk rasa dan kerusuhan Papua 2019Bagian dari Konflik PapuaUnjuk rasa di Kabupaten Sarmi, PapuaTanggal19 Agustus 2019 – 23 September 2019 (1 bulan dan 4 hari)LokasiSejumlah kabupaten dan kota di Provinsi Papua dan Papua Barat, demonstrasi kecil di kota-kota Indonesia lainnyaSebab Organisasi Papua Merdeka Kasus rasisme di Surabaya TujuanKemerdekaan PapuaStatus Pemblokiran akses Internet di Papua oleh Pemerintah Indonesia Pemerintah Indonesia menolak tuntutan referendum kemerdekaan Protes be...

Overview and history of coal production See also: Coal power in the United States Total US coal production, 1870–2018 Historical coal production of different countries Coal mining is an industry in transition in the United States. Production in 2019 was down 40% from the peak production of 1,171.8 million short tons (1,063 million metric tons) in 2008. Employment of 43,000 coal miners is down from a peak of 883,000 in 1923.[1] Generation of electricity is the largest user ...

Place du Forum Arles merupakan nama kota di Prancis yang letaknya di bagian selatan. Tepatnya di Provence-Alpes-Côte d'Azur. Pada tahun 2005, kota ini memiliki jumlah penduduk sebanyak 52.600 jiwa dan memiliki luas wilayah 758,93 km². Dengan kepadatan pendudukk 66 jiwa/km². Kota kembar York, Amerika Serikat Wisbech, Britania Raya Zhouzhuang, Tiongkok Vercelli, Italia Fulda, Jerman Sagné, Mauritania Pskov, Rusia Cubelles, Spanyol Jerez de la Frontera, Spanyol Kalymnos, Yunani Pranala ...

2015 film For the 2015 film of a similar name, see Utopians (film). UtopiaFilm posterDirected byHassan NazerWritten byAmir AghaeiProduced byChris RobbStarringMalalai ZikriaHannah SpearrittHomayoun ErshadiBhasker PatelCinematographyHákon PálssonAhmad KavoosiYiannis ManolopoulosEdited byReza JouzeMusic byArman Moosa PourProductioncompaniesTripswitch ProductionsWorld Film ProductionNay Media ProductionRelease date 26 July 2015 (2015-07-26) Running time87 minutesCountriesAfghanis...

Independence-class littoral combat ship of the United States Navy For other ships with the same name, see USS Augusta. USS Augusta being launched at Austal Shipyards. History United States NameAugusta NamesakeAugusta Awarded18 September 2018[3] BuilderAustal USA Laid down30 July 2021[4] Launched23 May 2022 Sponsored byLeigh Ingalls Saufley Christened17 December 2022[6] Acquired12 May 2023[1] Commissioned30 September 2023[2] HomeportNaval Base San Diego ...

Public university in Dijon, France University of BurgundyUniversité de BourgogneFormer nameUniversity of Dijon (1722-1984)TypePublicEstablished1722; 301 years ago (1722)[1]Budget242 million €RectorAlain BonninAdministrative staff2,774 including 1,519 professors. 2,700 adjunct professorsStudents30,917Undergraduates16,800Postgraduates9,400Doctoral students1,299LocationDijon, Bourgogne-Franche-Comté, France47°18′45″N 5°4′15″E / 47.31250°N ...

Selection of the Democratic Party nominee 2012 Democratic Party presidential primaries ← 2008 January 3 to June 5, 2012 2016 → Candidate Barack Obama Uncommitted John Wolfe Jr. Home state Illinois N/A Tennessee Delegate count 3,166 72 23 Contests won 56 0 0 Popular vote 6,158,064 426,336 117,033 Percentage 88.9% 6.1% 1.7% Barack Obama Previous Democratic nominee Barack Obama Democratic nominee Barack Obama 2012 U.S. presidential ele...

عبد الحميد بن عبد الله الآلوسي معلومات شخصية الميلاد سنة 1817 بغداد الوفاة 23 يوليو 1906 (88–89 سنة) بغداد مكان الدفن مقبرة الشيخ معروف مواطنة الدولة العثمانية الديانة الإسلام[1] مشكلة صحية عمى[1] إخوة وأخوات أبو الثناء الآلوسي عائلة الآلوس�...
青年佔領政治成立時間2014年4月25日創始人冼義哲邱柏瑋潘翰聲巫紫汝類型非營利組織重要人物冼義哲林佳諭張峻偉邱柏瑋羅丹口號大於十八,我要投票小於二三,我要參政青年佔領,全面參選網站<青年佔領政治>臉書頁粉絲團 青年佔領政治(Youth Occupy Politics)是一個台灣青年政治(英语:Youth politics)組織,致力於推動「第八次憲改」、下修投票與參選年齡、選制改革�...

1999 UK local government election 1999 Corby Borough Council election [1] ← 1995 6 May 1999 2003 → All 29 seats in the Corby Borough Council15 seats needed for a majority First party Second party Third party Party Labour Conservative Liberal Democrats Last election 24 seats, 67.4% 1 seat, 15.5% 2 seats, 5.1% Seats won 27 1 1 Seat change 3 0 1 Popular vote 6,021 2,061 758 Percentage 62.4% 21.4% 7.9% Swing 5.0% 5.9% 2.8% Map showin...

Restricted AreaNhà phát triểnMaster CreatingNhà phát hànhWhiptail InteractiveNền tảngMicrosoft WindowsPhát hành31 tháng 5 năm 2005Thể loạiHành động nhập vai thời gian thựcChế độ chơiChơi đơn, Chơi mạng Restricted Area là tựa game hành động nhập vai thời gian thực do hãng Master Creating của Đức phát triển và Whiptail Interactive phát hành vào năm 2005.[1] Cốt truyện Restricted Area lấy bối cảnh thế giới ...





