–Ē–≤–ĺ—Ź–ļ–ĺ–≤—č–Ņ—É–ļ–Ľ–į—Ź –Ľ–ł–Ĺ–∑–į –õ–łŐĀ–Ĺ–∑–į (–Ĺ–Ķ–ľ. Linse , –ĺ—ā –Ľ–į—ā. lens ‚ÄĒ —á–Ķ—á–Ķ–≤–ł—Ü–į) ‚ÄĒ –ī–Ķ—ā–į–Ľ—Ć –ł–∑ –Ņ—Ä–ĺ–∑—Ä–į—á–Ĺ–ĺ–≥–ĺ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ–ĺ–≥–ĺ –ľ–į—ā–Ķ—Ä–ł–į–Ľ–į, –ł–ľ–Ķ—é—Č–į—Ź –ī–≤–Ķ –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ—Ź—é—Č–ł–Ķ –Ņ–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ķ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ĺ–Ī–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ł–Ľ–ł –∂–Ķ –ĺ–ī–Ĺ—É –Ņ–Ľ–ĺ—Ā–ļ—É—é, –į –ī—Ä—É–≥—É—é ‚ÄĒ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ—É—é. –í –Ĺ–į—Ā—ā–ĺ—Ź—Č–Ķ–Ķ –≤—Ä–Ķ–ľ—Ź –≤—Ā—Ď —á–į—Č–Ķ –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź—é—ā—Ā—Ź –ł ¬ę–į—Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –Ľ–ł–Ĺ–∑—č ¬Ľ, —Ą–ĺ—Ä–ľ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ļ–ĺ—ā–ĺ—Ä—č—Ö –ĺ—ā–Ľ–ł—á–į–Ķ—ā—Ā—Ź –ĺ—ā —Ā—Ą–Ķ—Ä—č. –í –ļ–į—á–Ķ—Ā—ā–≤–Ķ –ľ–į—ā–Ķ—Ä–ł–į–Ľ–į –Ľ–ł–Ĺ–∑ –ĺ–Ī—č—á–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ľ–į—ā–Ķ—Ä–ł–į–Ľ—č , —ā–į–ļ–ł–Ķ –ļ–į–ļ —Ā—ā–Ķ–ļ–Ľ–ĺ , –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ —Ā—ā–Ķ–ļ–Ľ–ĺ , –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ—č , –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–∑—Ä–į—á–Ĺ—č–Ķ –Ņ–Ľ–į—Ā—ā–ľ–į—Ā—Ā—č –ł –ī—Ä—É–≥–ł–Ķ –ľ–į—ā–Ķ—Ä–ł–į–Ľ—č[ 1] –ł–Ĺ—Ą—Ä–į–ļ—Ä–į—Ā–Ĺ–ĺ–≥–ĺ –ł–∑–Ľ—É—á–Ķ–Ĺ–ł—Ź (–ļ–į–ļ –Ņ—Ä–į–≤–ł–Ľ–ĺ, –≥–Ķ—Ä–ľ–į–Ĺ–ł–Ļ , –ļ—Ä–Ķ–ľ–Ĺ–ł–Ļ , —á–Ķ—Ä–Ĺ—č–Ļ —Ā–Ķ–Ľ–Ķ–Ĺ , —Ą—ā–ĺ—Ä–ł–ī –ľ–į–≥–Ĺ–ł—Ź , —Ą—ā–ĺ—Ä–ł–ī –ļ–į–Ľ—Ć—Ü–ł—Ź –ł–Ľ–ł —Ā–Ķ–Ľ–Ķ–Ĺ–ł–ī —Ü–ł–Ĺ–ļ–į ).
–Ę–Ķ—Ä–ľ–ł–Ĺ ¬ę–Ľ–ł–Ĺ–∑–į¬Ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā —ā–į–ļ–∂–Ķ –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ļ –ī—Ä—É–≥–ł–ľ –Ņ—Ä–ł–Ī–ĺ—Ä–į–ľ –ł —Ź–≤–Ľ–Ķ–Ĺ–ł—Ź–ľ, –ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ĺ–į –ł–∑–Ľ—É—á–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—é –Ľ–ł–Ĺ–∑—č, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä:
–Ņ–Ľ–ĺ—Ā–ļ–ł–Ķ ¬ę–Ľ–ł–Ĺ–∑—謼, –ł–∑–≥–ĺ—ā–ĺ–≤–Ľ–Ķ–Ĺ–Ĺ—č–Ķ –ł–∑ –ľ–į—ā–Ķ—Ä–ł–į–Ľ–į —Ā –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–ľ –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź , –ł–∑–ľ–Ķ–Ĺ—Ź—é—Č–ł–ľ—Ā—Ź –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į;
–Ľ–ł–Ĺ–∑—č –§—Ä–Ķ–Ĺ–Ķ–Ľ—Ź ;–∑–ĺ–Ĺ–Ĺ–į—Ź –Ņ–Ľ–į—Ā—ā–ł–Ĺ–ļ–į –§—Ä–Ķ–Ĺ–Ķ–Ľ—Ź , –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—Č–į—Ź —Ź–≤–Ľ–Ķ–Ĺ–ł–Ķ –ī–ł—Ą—Ä–į–ļ—Ü–ł–ł ;¬ę–Ľ–ł–Ĺ–∑—謼 –≤–ĺ–∑–ī—É—Ö–į –≤ –į—ā–ľ–ĺ—Ā—Ą–Ķ—Ä–Ķ ‚ÄĒ –Ĺ–Ķ–ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ–ĺ—Ā—ā—Ć —Ā–≤–ĺ–Ļ—Ā—ā–≤, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ź –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź (–Ņ—Ä–ĺ—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤ –≤–ł–ī–Ķ –ľ–Ķ—Ä—Ü–į–Ĺ–ł—Ź –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –∑–≤—Ď–∑–ī –≤ –Ĺ–ĺ—á–Ĺ–ĺ–ľ –Ĺ–Ķ–Ī–Ķ);
–≥—Ä–į–≤–ł—ā–į—Ü–ł–ĺ–Ĺ–Ĺ–į—Ź –Ľ–ł–Ĺ–∑–į ‚ÄĒ –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č–Ļ –Ĺ–į –ľ–Ķ–∂–≥–į–Ľ–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö —ć—Ą—Ą–Ķ–ļ—ā –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–ľ–į–≥–Ĺ–ł—ā–Ĺ—č—Ö –≤–ĺ–Ľ–Ĺ –ľ–į—Ā—Ā–ł–≤–Ĺ—č–ľ–ł –ĺ–Ī—ä–Ķ–ļ—ā–į–ľ–ł;–ľ–į–≥–Ĺ–ł—ā–Ĺ–į—Ź –Ľ–ł–Ĺ–∑–į ‚ÄĒ —É—Ā—ā—Ä–ĺ–Ļ—Ā—ā–≤–ĺ, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—Č–Ķ–Ķ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–Ķ –ľ–į–≥–Ĺ–ł—ā–Ĺ–ĺ–Ķ –Ņ–ĺ–Ľ–Ķ –ī–Ľ—Ź —Ą–ĺ–ļ—É—Ā–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ—É—á–ļ–į –∑–į—Ä—Ź–∂–Ķ–Ĺ–Ĺ—č—Ö —á–į—Ā—ā–ł—Ü (–ł–ĺ–Ĺ–ĺ–≤ –ł–Ľ–ł —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤ ) –ł –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź—é—Č–Ķ–Ķ—Ā—Ź –≤ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ—č—Ö –ł –ł–ĺ–Ĺ–Ĺ—č—Ö –ľ–ł–ļ—Ä–ĺ—Ā–ļ–ĺ–Ņ–į—Ö ;–ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑—č, —Ā—Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ķ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–ĺ–Ļ –ł–Ľ–ł —á–į—Ā—ā—Ć—é –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –Ņ—Ä–ł —Ä–į—Ā—á—Ď—ā–Ķ —Ā–Ľ–ĺ–∂–Ĺ—č—Ö –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ.
–≤–∑—Ä—č–≤–Ĺ—č–Ķ –Ľ–ł–Ĺ–∑—č –≤ —Ź–ī–Ķ—Ä–Ĺ–ĺ–ľ –ĺ—Ä—É–∂–ł–ł ‚ÄĒ –Ĺ—É–∂–Ĺ—č –ī–Ľ—Ź –Ņ—Ä–ł–ī–į–Ĺ–ł—Ź —Ā—Ö–ĺ–ī—Ź—Č–Ķ–Ļ—Ā—Ź –≤–∑—Ä—č–≤–Ĺ–ĺ–Ļ –≤–ĺ–Ľ–Ĺ–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ĺ—Ä–ľ—č, —á—ā–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ī–Ľ—Ź —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –ĺ–Ī–∂–į—ā–ł—Ź –ĺ—ā—Ä–į–∂–į—ā–Ķ–Ľ—Ź –Ĺ–Ķ–Ļ—ā—Ä–ĺ–Ĺ–ĺ–≤ —Ā –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł–ľ—Ā—Ź –≤–Ĺ—É—ā—Ä–ł —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ –∑–į—Ä—Ź–ī–ĺ–ľ –ł–∑ –ī–Ķ–Ľ—Ź—Č–Ķ–≥–ĺ—Ā—Ź –≤–Ķ—Č–Ķ—Ā—ā–≤–į ‚ÄĒ –Ņ–Ľ—É—ā–ĺ–Ĺ–ł—Ź-239 , —É—Ä–į–Ĺ–į-235 –ł–Ľ–ł —É—Ä–į–Ĺ–į-233 , –Ľ–ł–Ī–ĺ –ł—Ö —Ā–Ņ–Ľ–į–≤–į. –ü—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ –ī–ĺ–≤–ĺ–Ľ—Ć–Ĺ–ĺ —Ā–Ľ–ĺ–∂–Ĺ—č–Ķ –Ņ–ĺ —Ą–ĺ—Ä–ľ–Ķ (—Ą–ĺ—Ä–ľ–į –ĺ—á–Ķ–Ĺ—Ć —ā–ĺ—á–Ĺ–ĺ —Ä–į—Ā—Ā—á–ł—ā–į–Ĺ–į) –ł–∑–ī–Ķ–Ľ–ł—Ź, –ł–∑ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ľ–Ķ–ī–Ľ–Ķ–Ĺ–Ĺ–ĺ –≥–ĺ—Ä—Ź—Č–Ķ–≥–ĺ –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č–ľ —Ā–ĺ—Ā—ā–į–≤–ĺ–ľ –≤–∑—Ä—č–≤—á–į—ā–ĺ–≥–ĺ –≤–Ķ—Č–Ķ—Ā—ā–≤–į —Ā –∑–į—Ā–Ķ–ļ—Ä–Ķ—á–Ķ–Ĺ–Ĺ—č–ľ —Ā–ĺ—Ā—ā–į–≤–ĺ–ľ, —ā–į–ļ –Ĺ–į–∑—č–≤–į–Ķ–ľ–ĺ–Ļ ¬ę–ľ–Ķ–ī–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤–∑—Ä—č–≤—á–į—ā–ļ–ł¬Ľ.
–°–≤–Ķ—ā –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ—Ź–Ķ—ā—Ā—Ź —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ —Ā—ā–Ķ–ļ–Ľ—Ź–Ĺ–Ĺ—č–ľ —Ā–ĺ—Ā—É–ī–ĺ–ľ, –Ĺ–į–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ—č–ľ –≤–ĺ–ī–ĺ–Ļ. –†–ĺ–ī–∂–Ķ—Ä –Ď—ć–ļ–ĺ–Ĺ , XIII –≤–Ķ–ļ –ě–Ī—ä–Ķ–ļ—ā–ł–≤ –ī–Ľ—Ź LSST , –Ņ–Ľ–į–Ĺ–ł—Ä—É–Ķ–ľ–ĺ–≥–ĺ —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ–į –ī–Ľ—Ź –ĺ–Ī–∑–ĺ—Ä–į –Ĺ–Ķ–Ī–į –°–Ľ–ĺ–≤–ĺ –Ľ–ł–Ĺ–∑–į lńďns —á–Ķ—á–Ķ–≤–ł—Ü—č , –Ņ–ĺ—ā–ĺ–ľ—É —á—ā–ĺ –ī–≤–ĺ—Ź–ļ–ĺ–≤—č–Ņ—É–ļ–Ľ–į—Ź –Ľ–ł–Ĺ–∑–į –ł–ľ–Ķ–Ķ—ā —Ą–ĺ—Ä–ľ—É —á–Ķ—á–Ķ–≤–ł—Ü—č. –õ–ł–Ĺ–∑–ĺ–Ļ —ā–į–ļ–∂–Ķ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–į—Ź —Ą–ł–≥—É—Ä–į [ 2]
–Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ —É—á—Ď–Ĺ—č–Ķ —É—ā–≤–Ķ—Ä–∂–ī–į—é—ā, —á—ā–ĺ –į—Ä—Ö–Ķ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–≤–ł–ī–Ķ—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —É–ļ–į–∑—č–≤–į—é—ā –Ĺ–į —ą–ł—Ä–ĺ–ļ–ĺ–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑ –≤ –ī—Ä–Ķ–≤–Ĺ–ĺ—Ā—ā–ł –Ĺ–į –Ņ—Ä–ĺ—ā—Ź–∂–Ķ–Ĺ–ł–ł –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö —ā—č—Ā—Ź—á–Ķ–Ľ–Ķ—ā–ł–Ļ[ 3] –Ľ–ł–Ĺ–∑–į –Ě–ł–ľ—Ä—É–ī–į ‚ÄĒ –į—Ä—ā–Ķ—Ą–į–ļ—ā –ł–∑ –≥–ĺ—Ä–Ĺ–ĺ–≥–ĺ —Ö—Ä—É—Ā—ā–į–Ľ—Ź , –ī–į—ā–ł—Ä—É–Ķ–ľ—č–Ļ VIII –≤–Ķ–ļ–ĺ–ľ (750 ‚ÄĒ710 –≥–≥.) –ī–ĺ –Ĺ–į—ą–Ķ–Ļ —ć—Ä—č, –ļ–ĺ—ā–ĺ—Ä—č–Ļ, –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ľ—Ā—Ź –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ —É–≤–Ķ–Ľ–ł—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ł–Ľ–ł –∑–į–∂–ł–≥–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ā—ā–Ķ–ļ–Ľ–į –Ľ–ł–Ī–ĺ –Ņ—Ä–Ķ–ī–Ĺ–į–∑–Ĺ–į—á–į–Ľ—Ā—Ź –ī–Ľ—Ź –ī—Ä—É–≥–ł—Ö —Ü–Ķ–Ľ–Ķ–Ļ[ 4] [ 5] [ 6] –Ķ–≥–ł–Ņ–Ķ—ā—Ā–ļ–ł–Ķ –ł–Ķ—Ä–ĺ–≥–Ľ–ł—Ą—č –ł–∑–ĺ–Ī—Ä–į–∂–į—é—ā ¬ę–Ņ—Ä–ĺ—Ā—ā—č–Ķ —Ā—ā–Ķ–ļ–Ľ—Ź–Ĺ–Ĺ—č–Ķ –ľ–Ķ–Ĺ–ł—Ā–ļ–ĺ–≤—č–Ķ –Ľ–ł–Ĺ–∑—謼[ 7]
–°–į–ľ—č–Ļ –ī—Ä–Ķ–≤–Ĺ–ł–Ļ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–Ĺ—č–Ļ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —É–Ņ–ĺ–ľ–ł–Ĺ–į–Ķ—ā—Ā—Ź –ĺ–Ī –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–ł –Ľ–ł–Ĺ–∑, –į –ł–ľ–Ķ–Ĺ–Ĺ–ĺ –∑–į–∂–ł–≥–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ā—ā–Ķ–ļ–Ľ–į, ‚ÄĒ –Ņ—Ć–Ķ—Ā–į –ź—Ä–ł—Ā—ā–ĺ—Ą–į–Ĺ–į ¬ę–ě–Ī–Ľ–į–ļ–į ¬Ľ (424 –≥. –ī–ĺ –Ĺ. —ć.)[ 8] –ü–Ľ–ł–Ĺ–ł–Ļ –°—ā–į—Ä—ą–ł–Ļ (I –≤–Ķ–ļ –Ĺ. —ć.) –Ņ–ĺ–ī—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā, —á—ā–ĺ –∑–į–∂–ł–≥–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ā—ā—Ď–ļ–Ľ–į –Ī—č–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –≤ –į–Ĺ—ā–ł—á–Ĺ–ĺ—Ā—ā–ł, –į –ł–ľ–Ķ–Ĺ–Ĺ–ĺ –≤ —Ä–ł–ľ—Ā–ļ–ł–Ļ –Ņ–Ķ—Ä–ł–ĺ–ī[ 9] –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–ł—Ä—É—é—Č–ł—Ö –Ľ–ł–Ĺ–∑ : –ĺ–Ĺ —É–Ņ–ĺ–ľ–ł–Ĺ–į–Ķ—ā, —á—ā–ĺ –Ě–Ķ—Ä–ĺ–Ĺ , –ļ–į–ļ –≥–ĺ–≤–ĺ—Ä—Ź—ā, —Ā–ľ–ĺ—ā—Ä–Ķ–Ľ –≥–Ľ–į–ī–ł–į—ā–ĺ—Ä—Ā–ļ–ł–Ķ –ł–≥—Ä—č, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ł–∑—É–ľ—Ä—É–ī (–Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤–ĺ–≥–Ĺ—É—ā—č–Ļ , —á—ā–ĺ–Ī—č –ł—Ā–Ņ—Ä–į–≤–ł—ā—Ć –Ī–Ľ–ł–∑–ĺ—Ä—É–ļ–ĺ—Ā—ā—Ć , —Ö–ĺ—ā—Ź –ĺ—ā—Ā—č–Ľ–ļ–į –Ĺ–Ķ —ā–ĺ—á–Ĺ–į)[ 10] –°–Ķ–Ĺ–Ķ–ļ–į –ú–Ľ–į–ī—ą–ł–Ļ (3 –≥. –ī–ĺ –Ĺ. —ć. ‚ÄĒ 65 –≥. –Ĺ. —ć.) –ĺ–Ņ–ł—Ā–į–Ľ–ł —É–≤–Ķ–Ľ–ł—á–ł–≤–į—é—Č–ł–Ļ —ć—Ą—Ą–Ķ–ļ—ā —Ā—ā–Ķ–ļ–Ľ—Ź–Ĺ–Ĺ–ĺ–≥–ĺ —ą–į—Ä–į, –Ĺ–į–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤–ĺ–ī–ĺ–Ļ.
–ü—ā–ĺ–Ľ–Ķ–ľ–Ķ–Ļ (II –≤–Ķ–ļ) –Ĺ–į–Ņ–ł—Ā–į–Ľ –ļ–Ĺ–ł–≥—É –Ņ–ĺ –ĺ–Ņ—ā–ł–ļ–Ķ –ė–Ī–Ĺ –°–į–Ľ–ĺ–ľ (X –≤–Ķ–ļ), —á–Ķ–Ļ –≤–ļ–Ľ–į–ī, –≤ —Ā–≤–ĺ—é –ĺ—á–Ķ—Ä–Ķ–ī—Ć, –Ī—č–Ľ —É–Ľ—É—á—ą–Ķ–Ĺ –ź–Ľ—Ć—Ö–į–∑–Ķ–Ĺ–ĺ–ľ (–ö–Ĺ–ł–≥–į –ĺ–Ī –ĺ–Ņ—ā–ł–ļ–Ķ –ě–Ņ—ā–ł–ļ–ł –ü—ā–ĺ–Ľ–Ķ–ľ–Ķ—Ź —Ā—ā–į–Ľ –ī–ĺ—Ā—ā—É–Ņ–Ķ–Ĺ –≤ –Ľ–į—ā–ł–Ĺ—Ā–ļ–ĺ–ľ –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī–Ķ –≤ XII –≤–Ķ–ļ–Ķ (–ē–≤–≥–Ķ–Ĺ–ł–Ļ –ü–į–Ľ–Ķ—Ä–ľ—Ā–ļ–ł–Ļ , 1154 –≥.). –ú–Ķ–∂–ī—É XI –ł XIII –≤–Ķ–ļ–į–ľ–ł –Ī—č–Ľ–ł –ł–∑–ĺ–Ī—Ä–Ķ—ā–Ķ–Ĺ—č ¬ę–ļ–į–ľ–Ĺ–ł –ī–Ľ—Ź —á—ā–Ķ–Ĺ–ł—Ź ¬Ľ. –≠—ā–ĺ –Ī—č–Ľ–ł –Ņ—Ä–ł–ľ–ł—ā–ł–≤–Ĺ—č–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ-–≤—č–Ņ—É–ļ–Ľ—č–Ķ –Ľ–ł–Ĺ–∑—č, –ł–∑–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į–Ĺ–Ĺ—č–Ķ –Ņ—É—ā–Ķ–ľ —Ä–į–∑—Ä–Ķ–∑–į–Ĺ–ł—Ź —Ā—ā–Ķ–ļ–Ľ—Ź–Ĺ–Ĺ–ĺ–Ļ —Ā—Ą–Ķ—Ä—č –Ņ–ĺ–Ņ–ĺ–Ľ–į–ľ. –°—Ä–Ķ–ī–Ĺ–Ķ–≤–Ķ–ļ–ĺ–≤—č–Ķ (XI –ł–Ľ–ł XII –≤–Ķ–ļ) –Ľ–ł–Ĺ–∑—č –í–ł—Ā–Ī—é –ł–∑ –≥–ĺ—Ä–Ĺ–ĺ–≥–ĺ —Ö—Ä—É—Ā—ā–į–Ľ—Ź –ľ–ĺ–≥–Ľ–ł –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī–Ĺ–į–∑–Ĺ–į—á–Ķ–Ĺ—č –ī–Ľ—Ź –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł—Ź –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –∑–į–∂–ł–≥–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —Ā—ā—Ď–ļ–ĺ–Ľ, –ĺ–ī–Ĺ–į–ļ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, —á—ā–ĺ –ł—Ö –ł–∑–≥–ĺ—ā–ĺ–≤–ł–Ľ–ł –ī–Ľ—Ź –ļ–į–ļ–ł—Ö-—ā–ĺ –ł–Ĺ—č—Ö —Ü–Ķ–Ľ–Ķ–Ļ[ 11]
–ě—á–ļ–ł –Ī—č–Ľ–ł –ł–∑–ĺ–Ī—Ä–Ķ—ā–Ķ–Ĺ—č –ļ–į–ļ —É—Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ ¬ę–ļ–į–ľ–Ĺ–Ķ–Ļ –ī–Ľ—Ź —á—ā–Ķ–Ĺ–ł—Ź¬Ľ –Ņ–Ķ—Ä–ł–ĺ–ī–į –í—č—Ā–ĺ–ļ–ĺ–≥–ĺ –°—Ä–Ķ–ī–Ĺ–Ķ–≤–Ķ–ļ–ĺ–≤—Ć—Ź –≤ –°–Ķ–≤–Ķ—Ä–Ĺ–ĺ–Ļ –ė—ā–į–Ľ–ł–ł –≤–ĺ –≤—ā–ĺ—Ä–ĺ–Ļ –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ķ XIII –≤–Ķ–ļ–į[ 12] –í–Ķ–Ĺ–Ķ—Ü–ł–ł –ł –§–Ľ–ĺ—Ä–Ķ–Ĺ—Ü–ł–ł –≤ –ļ–ĺ–Ĺ—Ü–Ķ XIII –≤–Ķ–ļ–į[ 13] –Ě–ł–ī–Ķ—Ä–Ľ–į–Ĺ–ī–į—Ö –ł –ď–Ķ—Ä–ľ–į–Ĺ–ł–ł [ 14] [ 15] [ 16] –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ľ–ł–ļ—Ä–ĺ—Ā–ļ–ĺ–Ņ–į –ĺ–ļ–ĺ–Ľ–ĺ 1595 –≥–ĺ–ī–į –ł —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ–į-—Ä–Ķ—Ą—Ä–į–ļ—ā–ĺ—Ä–į –≤ 1608 –≥–ĺ–ī—É ‚ÄĒ –ł —ā–ĺ—ā –ł –ī—Ä—É–≥–ĺ–Ļ –Ņ–ĺ—Ź–≤–ł–Ľ–ł—Ā—Ć –≤ —Ü–Ķ–Ĺ—ā—Ä–į—Ö –ł–∑–≥–ĺ—ā–ĺ–≤–Ľ–Ķ–Ĺ–ł—Ź –ĺ—á–ļ–ĺ–≤ –≤ –Ě–ł–ī–Ķ—Ä–Ľ–į–Ĺ–ī–į—Ö [ 17] [ 18]
–° –ł–∑–ĺ–Ī—Ä–Ķ—ā–Ķ–Ĺ–ł–Ķ–ľ —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ–į –≤ XVII –≤–Ķ–ļ–Ķ –ł –ľ–ł–ļ—Ä–ĺ—Ā–ļ–ĺ–Ņ–į –≤ –Ĺ–į—á–į–Ľ–Ķ XVIII –Ī—č–Ľ–ĺ –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —ć–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–ĺ–≤ —Ā —Ą–ĺ—Ä–ľ–į–ľ–ł –Ľ–ł–Ĺ–∑ –≤ —Ā—ā—Ä–Ķ–ľ–Ľ–Ķ–Ĺ–ł–ł –ł—Ā–Ņ—Ä–į–≤–ł—ā—Ć –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č–Ķ –≤ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł—Ö —Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ—ą–ł–Ī–ļ–ł. –ě–Ņ—ā–ł–ļ–ł –Ņ—č—ā–į–Ľ–ł—Ā—Ć –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ł—Ä–ĺ–≤–į—ā—Ć –Ľ–ł–Ĺ–∑—č —Ä–į–∑–Ľ–ł—á–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ—č –ļ—Ä–ł–≤–ł–∑–Ĺ—č, –ĺ—ą–ł–Ī–ĺ—á–Ĺ–ĺ –Ņ–ĺ–Ľ–į–≥–į—Ź, —á—ā–ĺ –ĺ—ą–ł–Ī–ļ–ł –≤–ĺ–∑–Ĺ–ł–ļ–Ľ–ł –ł–∑-–∑–į –ī–Ķ—Ą–Ķ–ļ—ā–ĺ–≤ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ĺ—Ä–ľ—č –ł—Ö –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ[ 19] –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź –ł —ć–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā—č –Ņ–ĺ–ļ–į–∑–į–Ľ–ł, —á—ā–ĺ –Ĺ–ł –ĺ–ī–ł–Ĺ –ĺ–ī–Ĺ–ĺ—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ĺ—č–Ļ –ĺ–Ī—ä–Ķ–ļ—ā–ł–≤ –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā —Ā—Ą–ĺ–ļ—É—Ā–ł—Ä–ĺ–≤–į—ā—Ć –≤—Ā–Ķ —Ü–≤–Ķ—ā–į. –≠—ā–ĺ –Ņ—Ä–ł–≤–Ķ–Ľ–ĺ –ļ –ł–∑–ĺ–Ī—Ä–Ķ—ā–Ķ–Ĺ–ł—é —Ā–ĺ—Ā—ā–į–≤–Ĺ–ĺ–Ļ –į—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č –ß–Ķ—Ā—ā–Ķ—Ä–ĺ–ľ –ú—É—Ä–ĺ–ľ –•–ĺ–Ľ–Ľ–ĺ–ľ –≤ –ź–Ĺ–≥–Ľ–ł–ł –≤ 1733 –≥–ĺ–ī—É, –ł–∑–ĺ–Ī—Ä–Ķ—ā–Ķ–Ĺ–ł–Ķ —ā–į–ļ–∂–Ķ –Ī—č–Ľ–ĺ –∑–į—Ź–≤–Ľ–Ķ–Ĺ–ĺ –į–Ĺ–≥–Ľ–ł—á–į–Ĺ–ł–Ĺ–ĺ–ľ –Ē–∂–ĺ–Ĺ–ĺ–ľ –Ē–ĺ–Ľ–Ľ–ĺ–Ĺ–ī–ĺ–ľ –≤ –Ņ–į—ā–Ķ–Ĺ—ā–Ķ 1758 –≥–ĺ–ī–į.
–°–ļ–≤–ĺ–∑—Ć –ļ–į–Ņ–Ľ–ł –ī–ĺ–∂–ī—Ź, –ī–Ķ–Ļ—Ā—ā–≤—É—é—Č–ł–Ķ –ļ–į–ļ –Ľ–ł–Ĺ–∑—č, –≤–ł–ī–Ķ–Ĺ –ľ–ĺ—Ā—ā –ó–ĺ–Ľ–ĺ—ā—č–Ķ –í–ĺ—Ä–ĺ—ā–į –†–į—Ā—ā–Ķ–Ĺ–ł–Ķ, –≤–ł–ī–ł–ľ–ĺ–Ķ —á–Ķ—Ä–Ķ–∑ –ī–≤–ĺ—Ź–ļ–ĺ–≤—č–Ņ—É–ļ–Ľ—É—é –Ľ–ł–Ĺ–∑—É
–í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā —Ą–ĺ—Ä–ľ —Ä–į–∑–Ľ–ł—á–į—é—ā —Ā–ĺ–Ī–ł—Ä–į—é—Č–ł–Ķ (–Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ) –ł —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–ł–Ķ (–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ) –Ľ–ł–Ĺ–∑—č. –ö –≥—Ä—É–Ņ–Ņ–Ķ —Ā–ĺ–Ī–ł—Ä–į—é—Č–ł—Ö –Ľ–ł–Ĺ–∑ –ĺ–Ī—č—á–Ĺ–ĺ –ĺ—ā–Ĺ–ĺ—Ā—Ź—ā –Ľ–ł–Ĺ–∑—č, —É –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —ā–ĺ–Ľ—Č–Ķ –ł—Ö –ļ—Ä–į—Ď–≤, –į –ļ –≥—Ä—É–Ņ–Ņ–Ķ —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–ł—Ö ‚ÄĒ –Ľ–ł–Ĺ–∑—č, –ļ—Ä–į—Ź –ļ–ĺ—ā–ĺ—Ä—č—Ö —ā–ĺ–Ľ—Č–Ķ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č. –°–Ľ–Ķ–ī—É–Ķ—ā –ĺ—ā–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ —ć—ā–ĺ –≤–Ķ—Ä–Ĺ–ĺ —ā–ĺ–Ľ—Ć–ļ–ĺ –Ķ—Ā–Ľ–ł –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź —É –ľ–į—ā–Ķ—Ä–ł–į–Ľ–į –Ľ–ł–Ĺ–∑—č –Ī–ĺ–Ľ—Ć—ą–Ķ, —á–Ķ–ľ —É –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī—č. –ē—Ā–Ľ–ł –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź –Ľ–ł–Ĺ–∑—č –ľ–Ķ–Ĺ—Ć—ą–Ķ, —Ā–ł—ā—É–į—Ü–ł—Ź –Ī—É–ī–Ķ—ā –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–Ļ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ņ—É–∑—č—Ä—Ď–ļ –≤–ĺ–∑–ī—É—Ö–į –≤ –≤–ĺ–ī–Ķ ‚ÄĒ –ī–≤–ĺ—Ź–ļ–ĺ–≤—č–Ņ—É–ļ–Ľ–į—Ź —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–į—Ź –Ľ–ł–Ĺ–∑–į.
–õ–ł–Ĺ–∑—č —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—ā—Ā—Ź, –ļ–į–ļ –Ņ—Ä–į–≤–ł–Ľ–ĺ, —Ā–≤–ĺ–Ķ–Ļ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł–Ľ–ĺ–Ļ (–ł–∑–ľ–Ķ—Ä—Ź–Ķ—ā—Ā—Ź –≤ –ī–ł–ĺ–Ņ—ā—Ä–ł—Ź—Ö ), –ł —Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ .
–Ē–Ľ—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–ł–Ī–ĺ—Ä–ĺ–≤ —Ā –ł—Ā–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –į–Ī–Ķ—Ä—Ä–į—Ü–ł–Ķ–Ļ (–Ņ—Ä–Ķ–∂–ī–Ķ –≤—Ā–Ķ–≥–ĺ ‚ÄĒ —Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ, –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł–Ķ–Ļ —Ā–≤–Ķ—ā–į , ‚ÄĒ –į—Ö—Ä–ĺ–ľ–į—ā—č –ł –į–Ņ–ĺ—Ö—Ä–ĺ–ľ–į—ā—č ) –≤–į–∂–Ĺ—č –ł –ł–Ĺ—č–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ľ–ł–Ĺ–∑ –ł –ł—Ö –ľ–į—ā–Ķ—Ä–ł–į–Ľ–ĺ–≤, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź , –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł–ł , –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć –Ņ–ĺ–≥–Ľ–ĺ—Č–Ķ–Ĺ–ł—Ź –ł –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć —Ä–į—Ā—Ā–Ķ—Ź–Ĺ–ł—Ź –ľ–į—ā–Ķ—Ä–ł–į–Ľ–į –≤ –≤—č–Ī—Ä–į–Ĺ–Ĺ–ĺ–ľ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–Ķ.
–ė–Ĺ–ĺ–≥–ī–į –Ľ–ł–Ĺ–∑—č/–Ľ–ł–Ĺ–∑–ĺ–≤—č–Ķ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č (—Ä–Ķ—Ą—Ä–į–ļ—ā–ĺ—Ä—č) —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ —Ä–į—Ā—Ā—á–ł—ā—č–≤–į—é—ā—Ā—Ź –Ĺ–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –≤ —Ā—Ä–Ķ–ī–į—Ö —Ā –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤—č—Ā–ĺ–ļ–ł–ľ –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–ľ –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź (—Ā–ľ. –ł–ľ–ľ–Ķ—Ä—Ā–ł–ĺ–Ĺ–Ĺ—č–Ļ –ľ–ł–ļ—Ä–ĺ—Ā–ļ–ĺ–Ņ , –ł–ľ–ľ–Ķ—Ä—Ā–ł–ĺ–Ĺ–Ĺ—č–Ķ –∂–ł–ī–ļ–ĺ—Ā—ā–ł ).
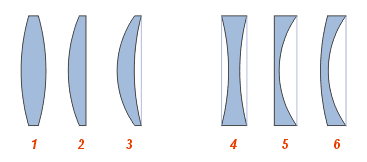
–í–ł–ī—č –Ľ–ł–Ĺ–∑: —Ā–ĺ–Ī–ł—Ä–į—é—Č–ł–Ķ : 1 ‚ÄĒ –ī–≤–ĺ—Ź–ļ–ĺ–≤—č–Ņ—É–ļ–Ľ–į—Ź; 2 ‚ÄĒ –Ņ–Ľ–ĺ—Ā–ļ–ĺ-–≤—č–Ņ—É–ļ–Ľ–į—Ź; 3 ‚ÄĒ –≤–ĺ–≥–Ĺ—É—ā–ĺ-–≤—č–Ņ—É–ļ–Ľ–į—Ź (–Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ļ (–≤—č–Ņ—É–ļ–Ľ—č–Ļ) –ľ–Ķ–Ĺ–ł—Ā–ļ); —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–ł–Ķ : 4 ‚ÄĒ –ī–≤–ĺ—Ź–ļ–ĺ–≤–ĺ–≥–Ĺ—É—ā–į—Ź; 5 ‚ÄĒ –Ņ–Ľ–ĺ—Ā–ļ–ĺ-–≤–ĺ–≥–Ĺ—É—ā–į—Ź; 6 ‚ÄĒ –≤—č–Ņ—É–ļ–Ľ–ĺ-–≤–ĺ–≥–Ĺ—É—ā–į—Ź (–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ļ (–≤–ĺ–≥–Ĺ—É—ā—č–Ļ) –ľ–Ķ–Ĺ–ł—Ā–ļ) –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑—č –ī–Ľ—Ź –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ą–ĺ—Ä–ľ—č –≤–ĺ–Ľ–Ĺ–ĺ–≤–ĺ–≥–ĺ —Ą—Ä–ĺ–Ĺ—ā–į . –ó–ī–Ķ—Ā—Ć –Ņ–Ľ–ĺ—Ā–ļ–ł–Ļ –≤–ĺ–Ľ–Ĺ–ĺ–≤–ĺ–Ļ —Ą—Ä–ĺ–Ĺ—ā —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ—Ä–ł –Ņ—Ä–ĺ—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–ł —á–Ķ—Ä–Ķ–∑ –Ľ–ł–Ĺ–∑—É –í—č–Ņ—É–ļ–Ľ–ĺ-–≤–ĺ–≥–Ĺ—É—ā–į—Ź –Ľ–ł–Ĺ–∑–į –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ľ–Ķ–Ĺ–ł—Ā–ļ–ĺ–ľ –ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ā–ĺ–Ī–ł—Ä–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ (—É—ā–ĺ–Ľ—Č–į–Ķ—ā—Ā—Ź –ļ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ķ), —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–Ķ–Ļ (—É—ā–ĺ–Ľ—Č–į–Ķ—ā—Ā—Ź –ļ –ļ—Ä–į—Ź–ľ) –ł–Ľ–ł —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–Ļ (—Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ —Ä–į–≤–Ĺ–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł). –Ę–į–ļ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ľ–ł–Ĺ–∑—č –ĺ—á–ļ–ĺ–≤ –ī–Ľ—Ź –Ī–Ľ–ł–∑–ĺ—Ä—É–ļ–ł—Ö ‚ÄĒ –ļ–į–ļ –Ņ—Ä–į–≤–ł–Ľ–ĺ, –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ľ–Ķ–Ĺ–ł—Ā–ļ–ł.
–í–ĺ–Ņ—Ä–Ķ–ļ–ł —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ď–Ĺ–Ĺ–ĺ–ľ—É –∑–į–Ī–Ľ—É–∂–ī–Ķ–Ĺ–ł—é, –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł–Ľ–į –ľ–Ķ–Ĺ–ł—Ā–ļ–į —Ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č–ľ–ł —Ä–į–ī–ł—É—Ā–į–ľ–ł –Ĺ–Ķ —Ä–į–≤–Ĺ–į –Ĺ—É–Ľ—é, –į –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–į, –ł –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ź –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź —Ā—ā–Ķ–ļ–Ľ–į –ł –ĺ—ā —ā–ĺ–Ľ—Č–ł–Ĺ—č –Ľ–ł–Ĺ–∑—č. –ú–Ķ–Ĺ–ł—Ā–ļ, —Ü–Ķ–Ĺ—ā—Ä—č –ļ—Ä–ł–≤–ł–∑–Ĺ—č –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—Ö–ĺ–ī—Ź—ā—Ā—Ź –≤ –ĺ–ī–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ļ–ĺ–Ĺ—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ľ–ł–Ĺ–∑–ĺ–Ļ (–ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł–Ľ–į –≤—Ā–Ķ–≥–ī–į –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–į).
–ě—ā–Ľ–ł—á–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ —Ā–ĺ–Ī–ł—Ä–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ–Ī–ł—Ä–į—ā—Ć –Ņ–į–ī–į—é—Č–ł–Ķ –Ĺ–į –Ķ—Ď –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć –Ľ—É—á–ł –≤ –ĺ–ī–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ–ĺ –ī—Ä—É–≥—É—é —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ľ–ł–Ĺ–∑—č.
–ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—č –Ľ–ł–Ĺ–∑—č:
N
N
{\displaystyle NN}
–ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–į—Ź –ĺ—Ā—Ć ‚ÄĒ –Ņ—Ä—Ź–ľ–į—Ź –Ľ–ł–Ĺ–ł—Ź, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ —Ü–Ķ–Ĺ—ā—Ä—č —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ, –ĺ–≥—Ä–į–Ĺ–ł—á–ł–≤–į—é—Č–ł—Ö –Ľ–ł–Ĺ–∑—É;
O
{\displaystyle O}
[ 20] –ē—Ā–Ľ–ł –Ĺ–į –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –Ņ–Ķ—Ä–Ķ–ī —Ā–ĺ–Ī–ł—Ä–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ľ–ł–Ĺ–∑–ĺ–Ļ –Ņ–ĺ–ľ–Ķ—Ā—ā–ł—ā—Ć —Ā–≤–Ķ—ā—Ź—Č—É—é—Ā—Ź —ā–ĺ—á–ļ—É
S
{\displaystyle S}
–Ņ—Ä–Ķ–Ľ–ĺ–ľ–ł–≤—ą–ł—Ā—Ć , –į –Ľ—É—á–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł–Ķ –Ĺ–Ķ —á–Ķ—Ä–Ķ–∑ —Ü–Ķ–Ĺ—ā—Ä, –Ī—É–ī—É—ā –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ—Ź—ā—Ć—Ā—Ź –≤ —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ—Ā–ł –ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ—É—ā—Ā—Ź –Ĺ–į –Ĺ–Ķ–Ļ –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ—á–ļ–Ķ
F
{\displaystyle F}
S
{\displaystyle S}
—Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ —Ą–ĺ–ļ—É—Ā–į , –ł–Ľ–ł –Ņ—Ä–ĺ—Ā—ā–ĺ —Ą–ĺ–ļ—É—Ā–į .
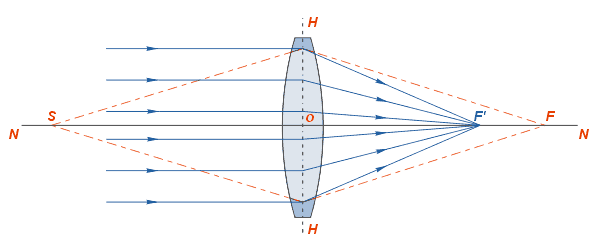
–ē—Ā–Ľ–ł –Ĺ–į –Ľ–ł–Ĺ–∑—É –Ī—É–ī–Ķ—ā –Ņ–į–ī–į—ā—Ć —Ā–≤–Ķ—ā –ĺ—ā –ĺ—á–Ķ–Ĺ—Ć —É–ī–į–Ľ—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į, –Ľ—É—á–ł –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā—Ć –ł–ī—É—Č–ł–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č–ľ –Ņ—É—á–ļ–ĺ–ľ, —ā–ĺ –Ĺ–į –≤—č—Ö–ĺ–ī–Ķ –ł–∑ –Ĺ–Ķ—Ď –Ľ—É—á–ł –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ—Ź—é—ā—Ā—Ź –Ņ–ĺ–ī –Ī–ĺŐĀ–Ľ—Ć—ą–ł–ľ —É–≥–Ľ–ĺ–ľ, –ł —ā–ĺ—á–ļ–į
F
{\displaystyle F}
F
′
{\displaystyle F'}
—Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ .
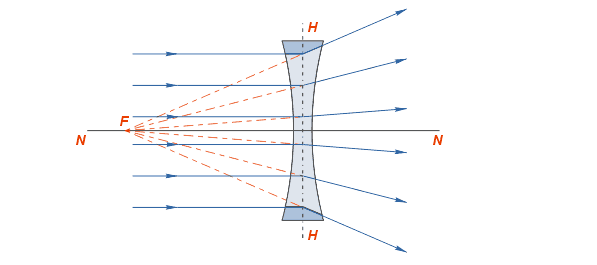
–õ—É—á–ł, –Ņ–į–ī–į—é—Č–ł–Ķ –Ĺ–į —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č—É—é –Ľ–ł–Ĺ–∑—É, –Ĺ–į –≤—č—Ö–ĺ–ī–Ķ –ł–∑ –Ĺ–Ķ—Ď –Ī—É–ī—É—ā –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ—Ź—ā—Ć—Ā—Ź –≤ —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –ļ—Ä–į—Ď–≤ –Ľ–ł–Ĺ–∑—č, —ā–ĺ –Ķ—Ā—ā—Ć —Ä–į—Ā—Ā–Ķ–ł–≤–į—ā—Ć—Ā—Ź. –ē—Ā–Ľ–ł —ć—ā–ł –Ľ—É—á–ł –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–ł—ā—Ć –≤ –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł —ā–į–ļ, –ļ–į–ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –Ņ—É–Ĺ–ļ—ā–ł—Ä–Ĺ–ĺ–Ļ –Ľ–ł–Ĺ–ł–Ķ–Ļ, —ā–ĺ –ĺ–Ĺ–ł —Ā–ĺ–Ļ–ī—É—ā—Ā—Ź –≤ –ĺ–ī–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ
F
{\displaystyle F}
–ú–Ĺ–ł–ľ—č–Ļ —Ą–ĺ–ļ—É—Ā —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–Ķ–Ļ –Ľ–ł–Ĺ–∑—č –°—Ö–ĺ–ī—Ź—Č–ł–Ķ—Ā—Ź –Ľ—É—á–ł —Ā–Ľ–Ķ–≤–į –ĺ—ā –Ľ–ł–Ĺ–∑—č —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –Ľ—É—á–į–ľ–ł, –ĺ—ā—Ä–į–∂–Ķ–Ĺ–Ĺ—č–ľ–ł –ĺ—ā –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –Ľ–ł–Ĺ–∑—č, –ł –Ĺ–Ķ —Ā–≤—Ź–∑–į–Ĺ—č —Ā –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ–ľ –ľ–Ĺ–ł–ľ–ĺ–≥–ĺ —Ą–ĺ–ļ—É—Ā–į –°–ļ–į–∑–į–Ĺ–Ĺ–ĺ–Ķ –ĺ —Ą–ĺ–ļ—É—Ā–Ķ –Ĺ–į –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ—Ā–ł –≤ —Ä–į–≤–Ĺ–ĺ–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –ĺ—ā–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –ł –ļ —ā–Ķ–ľ —Ā–Ľ—É—á–į—Ź–ľ, –ļ–ĺ–≥–ī–į –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į –Ĺ–į–ļ–Ľ–ĺ–Ĺ–Ĺ–ĺ–Ļ –Ľ–ł–Ĺ–ł–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —Ü–Ķ–Ĺ—ā—Ä –Ľ–ł–Ĺ–∑—č –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ –ļ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ—Ā–ł. –ü–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į—Ź –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ—Ā–ł, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–į—Ź –≤ —Ą–ĺ–ļ—É—Ā–Ķ –Ľ–ł–Ĺ–∑—č, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć—é .
–°–ĺ–Ī–ł—Ä–į—é—Č–ł–Ķ –Ľ–ł–Ĺ–∑—č –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ—č –ļ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā—É –Ľ—é–Ī–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ, –≤—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ —á–Ķ–≥–ĺ –Ľ—É—á–ł –Ņ—Ä–ł –Ņ—Ä–ĺ—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–ł —á–Ķ—Ä–Ķ–∑ –Ľ–ł–Ĺ–∑—É –ľ–ĺ–≥—É—ā —Ā–ĺ–Ī–ł—Ä–į—ā—Ć—Ā—Ź –ļ–į–ļ —Ā –ĺ–ī–Ĺ–ĺ–Ļ, —ā–į–ļ –ł —Ā –ī—Ä—É–≥–ĺ–Ļ –Ķ—Ď —Ā—ā–ĺ—Ä–ĺ–Ĺ—č. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ľ–ł–Ĺ–∑–į –ł–ľ–Ķ–Ķ—ā –ī–≤–į —Ą–ĺ–ļ—É—Ā–į ‚ÄĒ –Ņ–Ķ—Ä–Ķ–ī–Ĺ–ł–Ļ –ł –∑–į–ī–Ĺ–ł–Ļ . –†–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ—č –ĺ–Ĺ–ł –Ĺ–į –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ—Ā–ł –Ņ–ĺ –ĺ–Ī–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –Ľ–ł–Ĺ–∑—č –Ĺ–į —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –ĺ—ā –≥–Ľ–į–≤–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ľ–ł–Ĺ–∑—č.
–ß–į—Ā—ā–ĺ –≤ —ā–Ķ—Ö–Ĺ–ł–ļ–Ķ –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑—č (–Ľ—É–Ņ—č ) –ł –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź –ļ–į–ļ 2√ó, 3√ó –ł —ā. –ī. –í –ī–į–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ
Γ őď -->
d
=
F
+
d
F
=
d
F
+
1
{\displaystyle \Gamma _{d}={\frac {F+d}{F}}={\frac {d}{F}}+1}
F
{\displaystyle F}
d
{\displaystyle d}
[ 21] [ 22]
–õ–ł–Ĺ–∑–į, –ī–Ľ—Ź –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ–Ľ—Č–ł–Ĺ–į –Ņ—Ä–ł–Ĺ—Ź—ā–į —Ä–į–≤–Ĺ–ĺ–Ļ –Ĺ—É–Ľ—é, –≤ –ĺ–Ņ—ā–ł–ļ–Ķ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź ¬ę—ā–ĺ–Ĺ–ļ–ĺ–Ļ¬Ľ. –Ē–Ľ—Ź —ā–į–ļ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č –Ņ–ĺ–ļ–į–∑—č–≤–į—é—ā –Ĺ–Ķ –ī–≤–Ķ –≥–Ľ–į–≤–Ĺ—č—Ö –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł , –į –ĺ–ī–Ĺ—É, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ļ–į–ļ –Ī—č —Ā–Ľ–ł–≤–į—é—ā—Ā—Ź –≤–ľ–Ķ—Ā—ā–Ķ –Ņ–Ķ—Ä–Ķ–ī–Ĺ—Ź—Ź –ł –∑–į–ī–Ĺ—Ź—Ź.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ —Ö–ĺ–ī–į –Ľ—É—á–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –≤ —ā–ĺ–Ĺ–ļ–ĺ–Ļ —Ā–ĺ–Ī–ł—Ä–į—é—Č–Ķ–Ļ –Ľ–ł–Ĺ–∑–Ķ. –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ –≤–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź –ī–≤—É–ľ—Ź —Ā–≤–ĺ–Ļ—Ā—ā–≤–į–ľ–ł —ā–ĺ–Ĺ–ļ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č:
–Ľ—É—á, –Ņ—Ä–ĺ—ą–Ķ–ī—ą–ł–Ļ —á–Ķ—Ä–Ķ–∑ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł–Ļ —Ü–Ķ–Ĺ—ā—Ä –Ľ–ł–Ĺ–∑—č, –Ĺ–Ķ –ľ–Ķ–Ĺ—Ź–Ķ—ā —Ā–≤–ĺ–Ķ–≥–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź;
–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č–Ķ –Ľ—É—á–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł–Ķ —á–Ķ—Ä–Ķ–∑ –Ľ–ł–Ĺ–∑—É, —Ā—Ö–ĺ–ī—Ź—ā—Ā—Ź –≤ —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł. –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ľ—É—á
S
A
{\displaystyle SA}
A
{\displaystyle A}
O
B
{\displaystyle OB}
S
A
{\displaystyle SA}
O
{\displaystyle O}
O
B
{\displaystyle OB}
B
{\displaystyle B}
S
A
{\displaystyle SA}
S
A
{\displaystyle SA}
A
B
{\displaystyle AB}
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –ī—Ä—É–≥–ł–Ķ –Ľ—É—á–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ľ—É—á
S
P
Q
{\displaystyle SPQ}
–ě–Ī–ĺ–∑–Ĺ–į—á–ł–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ
S
O
{\displaystyle SO}
u
{\displaystyle u}
O
D
{\displaystyle OD}
v
{\displaystyle v}
O
F
{\displaystyle OF}
f
{\displaystyle f}
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ī–≤–Ķ –Ņ–į—Ä—č –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤:
△ ‚Ė≥ -->
S
O
A
{\displaystyle \triangle SOA}
△ ‚Ė≥ -->
O
F
B
{\displaystyle \triangle OFB}
△ ‚Ė≥ -->
D
O
A
{\displaystyle \triangle DOA}
△ ‚Ė≥ -->
D
F
B
{\displaystyle \triangle DFB}
O
A
u
=
B
F
f
;
O
A
v
=
B
F
v
− ‚ąí -->
f
.
{\displaystyle {\frac {OA}{u}}={\frac {BF}{f}};\qquad {\frac {OA}{v}}={\frac {BF}{v-f}}.}
–†–į–∑–ī–Ķ–Ľ–ł–≤ –Ņ–Ķ—Ä–≤—É—é –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—é –Ĺ–į –≤—ā–ĺ—Ä—É—é, –Ņ–ĺ–Ľ—É—á–ł–ľ
v
u
=
v
− ‚ąí -->
f
f
;
v
u
=
v
f
− ‚ąí -->
1.
{\displaystyle {\frac {v}{u}}={\frac {v-f}{f}};\qquad {\frac {v}{u}}={\frac {v}{f}}-1.}
–ü–ĺ—Ā–Ľ–Ķ –ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ĺ–Ī–Ķ–ł—Ö —á–į—Ā—ā–Ķ–Ļ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ĺ–į v –ł –Ņ–Ķ—Ä–Ķ–≥—Ä—É–Ņ–Ņ–ł—Ä–ĺ–≤–ļ–ł —á–Ľ–Ķ–Ĺ–ĺ–≤, –Ņ—Ä–ł—Ö–ĺ–ī–ł–ľ –ļ –ĺ–ļ–ĺ–Ĺ—á–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ
1
u
+
1
v
=
1
f
{\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}}}
–≥–ī–Ķ
f
{\displaystyle f}
–•–ĺ–ī –Ľ—É—á–Ķ–Ļ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –Ľ–ł–Ĺ–∑ —Ā—ā—Ä–ĺ–ł—ā—Ā—Ź —ā–Ķ–ľ–ł –∂–Ķ –ľ–Ķ—ā–ĺ–ī–į–ľ–ł, —á—ā–ĺ –ł –ī–Ľ—Ź –ĺ–ī–ł–Ĺ–ĺ—á–Ĺ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā–ł—Ā—ā–Ķ–ľ—É –ł–∑ –ī–≤—É—Ö –Ľ–ł–Ĺ–∑, –ĺ–ī–Ĺ–į –ł–∑ –ļ–ĺ—ā–ĺ—Ä—č—Ö –ł–ľ–Ķ–Ķ—ā —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ
O
F
{\displaystyle OF}
O
2
F
2
{\displaystyle O_{2}F_{2}}
S
A
B
{\displaystyle SAB}
A
B
{\displaystyle AB}
C
{\displaystyle C}
–ė–∑ —ā–ĺ—á–ļ–ł
O
2
{\displaystyle O_{2}}
O
2
E
{\displaystyle O_{2}E}
A
B
{\displaystyle AB}
E
{\displaystyle E}
A
B
{\displaystyle AB}
C
E
{\displaystyle CE}
D
{\displaystyle D}
S
{\displaystyle S}
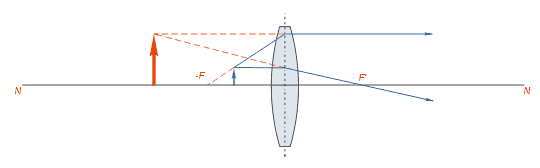
–ü—Ä–ł –ł–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–ł –Ľ–ł–Ĺ–∑ –Ī—č–Ľ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ—ā—Ź—Č–Ķ–Ļ—Ā—Ź —ā–ĺ—á–ļ–ł –≤ —Ą–ĺ–ļ—É—Ā–Ķ –Ľ–ł–Ĺ–∑—č. –õ—É—á–ł, –Ņ–į–ī–į—é—Č–ł–Ķ –Ĺ–į –Ľ–ł–Ĺ–∑—É —Ā–Ľ–Ķ–≤–į, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—ā —á–Ķ—Ä–Ķ–∑ –Ķ—Ď –∑–į–ī–Ĺ–ł–Ļ —Ą–ĺ–ļ—É—Ā, –į –Ņ–į–ī–į—é—Č–ł–Ķ —Ā–Ņ—Ä–į–≤–į ‚ÄĒ —á–Ķ—Ä–Ķ–∑ –Ņ–Ķ—Ä–Ķ–ī–Ĺ–ł–Ļ —Ą–ĺ–ļ—É—Ā. –°–Ľ–Ķ–ī—É–Ķ—ā —É—á–Ķ—Ā—ā—Ć, —á—ā–ĺ —É —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–ł—Ö –Ľ–ł–Ĺ–∑, –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā, –∑–į–ī–Ĺ–ł–Ļ —Ą–ĺ–ļ—É—Ā —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ —Ā–Ņ–Ķ—Ä–Ķ–ī–ł –Ľ–ł–Ĺ–∑—č, –į –Ņ–Ķ—Ä–Ķ–ī–Ĺ–ł–Ļ –Ņ–ĺ–∑–į–ī–ł.
–ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑–ĺ–Ļ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–≤, –ł–ľ–Ķ—é—Č–ł—Ö –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—É—é —Ą–ĺ—Ä–ľ—É –ł —Ä–į–∑–ľ–Ķ—Ä—č, –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ: –ī–ĺ–Ņ—É—Ā—ā–ł–ľ, –Ľ–ł–Ĺ–ł—Ź AB –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ĺ–Ī—ä–Ķ–ļ—ā, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł–Ļ—Ā—Ź –Ĺ–į –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –ĺ—ā –Ľ–ł–Ĺ–∑—č, –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–Ķ–≤—č—ą–į—é—Č–Ķ–ľ –Ķ—Ď —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –ě—ā –ļ–į–∂–ī–ĺ–Ļ —ā–ĺ—á–ļ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į —á–Ķ—Ä–Ķ–∑ –Ľ–ł–Ĺ–∑—É –Ņ—Ä–ĺ–Ļ–ī—Ď—ā –Ī–Ķ—Ā—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ľ—É—á–Ķ–Ļ, –ł–∑ –ļ–ĺ—ā–ĺ—Ä—č—Ö, –ī–Ľ—Ź –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ —Ā—Ö–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ —Ö–ĺ–ī —ā–ĺ–Ľ—Ć–ļ–ĺ —ā—Ä—Ď—Ö –Ľ—É—á–Ķ–Ļ.
–Ę—Ä–ł –Ľ—É—á–į, –ł—Ā—Ö–ĺ–ī—Ź—Č–ł–Ķ –ł–∑ —ā–ĺ—á–ļ–ł
A
{\displaystyle A}
A
1
B
1
{\displaystyle A_{1}B_{1}}
–ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –ł –Ņ–Ķ—Ä–Ķ–≤—Ď—Ä–Ĺ—É—ā—č–ľ .
–í –ī–į–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –≤ —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ–ĺ–ľ —Ą–ĺ–ļ—É—Ā–Ķ –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł
F
F
{\displaystyle FF}
F
′
F
′
{\displaystyle F'F'}
–Ē–į–Ľ–Ķ–Ķ –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ—č —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ —Ā–Ľ—É—á–į–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į, –Ņ–ĺ–ľ–Ķ—Č—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö –ĺ—ā –Ľ–ł–Ĺ–∑—č.
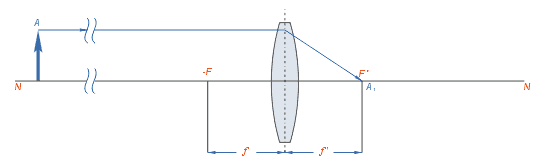
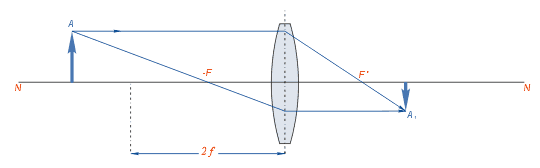
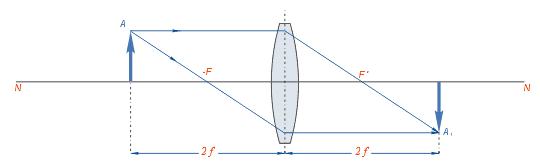
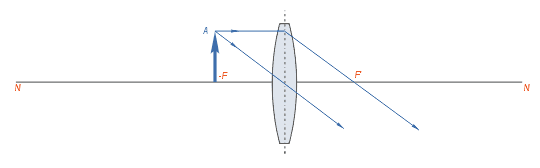
–ē—Ā–Ľ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ī–į–Ľ—Ď–ļ–ĺ–ľ –ĺ—ā –Ľ–ł–Ĺ–∑—č —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł, —ā–ĺ –Ķ–≥–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –≤ –∑–į–ī–Ĺ–Ķ–ľ —Ą–ĺ–ļ—É—Ā–Ķ –Ľ–ł–Ĺ–∑—č F‚Äô –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ, –Ņ–Ķ—Ä–Ķ–≤—Ď—Ä–Ĺ—É—ā—č–ľ –ł —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–Ĺ—č–ľ –ī–ĺ –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā–ĺ—á–ļ–ł. –ē—Ā–Ľ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ņ—Ä–ł–Ī–Ľ–ł–∂—Ď–Ĺ –ļ –Ľ–ł–Ĺ–∑–Ķ –ł –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł, –Ņ—Ä–Ķ–≤—č—ą–į—é—Č–Ķ–ľ –ī–≤–ĺ–Ļ–Ĺ–ĺ–Ķ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑—č, —ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ķ–≥–ĺ –Ī—É–ī–Ķ—ā –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ, –Ņ–Ķ—Ä–Ķ–≤—Ď—Ä–Ĺ—É—ā—č–ľ –ł —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–Ĺ—č–ľ –ł —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–ł—ā—Ā—Ź –∑–į –≥–Ľ–į–≤–Ĺ—č–ľ —Ą–ĺ–ļ—É—Ā–ĺ–ľ –Ĺ–į –ĺ—ā—Ä–Ķ–∑–ļ–Ķ –ľ–Ķ–∂–ī—É –Ĺ–ł–ľ –ł –ī–≤–ĺ–Ļ–Ĺ—č–ľ —Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ. –ē—Ā–Ľ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ņ–ĺ–ľ–Ķ—Č—Ď–Ĺ –Ĺ–į –ī–≤–ĺ–Ļ–Ĺ–ĺ–ľ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –ĺ—ā –Ľ–ł–Ĺ–∑—č, —ā–ĺ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ņ–ĺ –ī—Ä—É–≥—É—é —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ľ–ł–Ĺ–∑—č –Ĺ–į –ī–≤–ĺ–Ļ–Ĺ–ĺ–ľ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –ĺ—ā –Ĺ–Ķ—Ď. –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ, –Ņ–Ķ—Ä–Ķ–≤—Ď—Ä–Ĺ—É—ā—č–ľ –ł —Ä–į–≤–Ĺ—č–ľ –Ņ–ĺ –≤–Ķ–Ľ–ł—á–ł–Ĺ–Ķ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā—É. –ē—Ā–Ľ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ņ–ĺ–ľ–Ķ—Č—Ď–Ĺ –ľ–Ķ–∂–ī—É –Ņ–Ķ—Ä–Ķ–ī–Ĺ–ł–ľ —Ą–ĺ–ļ—É—Ā–ĺ–ľ –ł –ī–≤–ĺ–Ļ–Ĺ—č–ľ —Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ, —ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ī—É–ī–Ķ—ā –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –∑–į –ī–≤–ĺ–Ļ–Ĺ—č–ľ —Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ –ł –Ī—É–ī–Ķ—ā –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ, –Ņ–Ķ—Ä–Ķ–≤—Ď—Ä–Ĺ—É—ā—č–ľ –ł —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–Ĺ—č–ľ. –ē—Ā–Ľ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –≤ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ–ī–Ĺ–Ķ–≥–ĺ –≥–Ľ–į–≤–Ĺ–ĺ–≥–ĺ —Ą–ĺ–ļ—É—Ā–į –Ľ–ł–Ĺ–∑—č, —ā–ĺ –Ľ—É—á–ł, –Ņ—Ä–ĺ–Ļ–ī—Ź —á–Ķ—Ä–Ķ–∑ –Ľ–ł–Ĺ–∑—É, –Ņ–ĺ–Ļ–ī—É—ā –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ, –ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ľ–ĺ–∂–Ķ—ā –Ņ–ĺ–Ľ—É—á–ł—ā—Ć—Ā—Ź –Ľ–ł—ą—Ć –≤ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł. –ē—Ā–Ľ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ņ–ĺ–ľ–Ķ—Ā—ā–ł—ā—Ć –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł, –ľ–Ķ–Ĺ—Ć—ą–Ķ–ľ –≥–Ľ–į–≤–Ĺ–ĺ–≥–ĺ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, —ā–ĺ –Ľ—É—á–ł –≤—č–Ļ–ī—É—ā –ł–∑ –Ľ–ł–Ĺ–∑—č —Ä–į—Ā—Ö–ĺ–ī—Ź—Č–ł–ľ—Ā—Ź –Ņ—É—á–ļ–ĺ–ľ, –Ĺ–ł–≥–ī–Ķ –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—Ź—Ā—Ć. –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ł —ć—ā–ĺ–ľ –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –ľ–Ĺ–ł–ľ–ĺ–Ķ, –Ņ—Ä—Ź–ľ–ĺ–Ķ –ł —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–Ĺ–ĺ–Ķ, —ā–ĺ –Ķ—Ā—ā—Ć –≤ –ī–į–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –Ľ–ł–Ĺ–∑–į —Ä–į–Ī–ĺ—ā–į–Ķ—ā –ļ–į–ļ –Ľ—É–Ņ–į. –Ě–Ķ—ā—Ä—É–ī–Ĺ–ĺ –∑–į–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ –Ņ—Ä–ł –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–ł–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į –ł–∑ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł –ļ –Ņ–Ķ—Ä–Ķ–ī–Ĺ–Ķ–ľ—É —Ą–ĺ–ļ—É—Ā—É –Ľ–ł–Ĺ–∑—č –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —É–ī–į–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—ā –∑–į–ī–Ĺ–Ķ–≥–ĺ —Ą–ĺ–ļ—É—Ā–į –ł –Ņ–ĺ –ī–ĺ—Ā—ā–ł–∂–Ķ–Ĺ–ł–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–ľ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ–ī–Ĺ–Ķ–≥–ĺ —Ą–ĺ–ļ—É—Ā–į –ĺ–ļ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –≤ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł –ĺ—ā –Ĺ–Ķ–≥–ĺ.
–≠—ā–į –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć –ł–ľ–Ķ–Ķ—ā –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –≤ –Ņ—Ä–į–ļ—ā–ł–ļ–Ķ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –≤–ł–ī–ĺ–≤ —Ą–ĺ—ā–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö —Ä–į–Ī–ĺ—ā, –Ņ–ĺ—ć—ā–ĺ–ľ—É –ī–Ľ—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ľ–Ķ–∂–ī—É —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ –ĺ—ā –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į –ī–ĺ –Ľ–ł–Ĺ–∑—č –ł –ĺ—ā –Ľ–ł–Ĺ–∑—č –ī–ĺ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –∑–Ĺ–į—ā—Ć –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—É—é —Ą–ĺ—Ä–ľ—É–Ľ—É –Ľ–ł–Ĺ–∑—č .
–†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–į –ī–ĺ —Ü–Ķ–Ĺ—ā—Ä–į –Ľ–ł–Ĺ–∑—č –ł –ĺ—ā —ā–ĺ—á–ļ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –ī–ĺ —Ü–Ķ–Ĺ—ā—Ä–į –Ľ–ł–Ĺ–∑—č –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ—č–ľ–ł —Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ–ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź–ľ–ł .
–≠—ā–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –Ĺ–į—Ö–ĺ–ī—Ź—ā—Ā—Ź –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ľ–Ķ–∂–ī—É —Ā–ĺ–Ī–ĺ–Ļ –ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ, –Ĺ–į–∑—č–≤–į–Ķ–ľ–ĺ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ —ā–ĺ–Ĺ–ļ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č (–≤–Ņ–Ķ—Ä–≤—č–Ķ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ļ –ė—Ā–į–į–ļ–ĺ–ľ –Ď–į—Ä—Ä–ĺ—É ):
1
u
+
1
v
=
1
f
{\displaystyle {1 \over u}+{1 \over v}={1 \over f}}
–≥–ī–Ķ
u
{\displaystyle u}
v
{\displaystyle v}
f
{\displaystyle f}
–≥–Ľ–į–≤–Ĺ—č—Ö –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–Ķ–Ļ .
–Ē–Ľ—Ź –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź —ā–ĺ–Ļ –ł–Ľ–ł –ł–Ĺ–ĺ–Ļ –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –Ņ—Ä–ł –ī–≤—É—Ö –ł–∑–≤–Ķ—Ā—ā–Ĺ—č—Ö –Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ–ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź–ľ–ł:
f
=
v
⋅ ‚čÖ -->
u
v
+
u
{\displaystyle f={{v\cdot u} \over {v+u}}}
u
=
f
⋅ ‚čÖ -->
v
v
− ‚ąí -->
f
{\displaystyle u={{f\cdot v} \over {v-f}}}
v
=
f
⋅ ‚čÖ -->
u
u
− ‚ąí -->
f
{\displaystyle v={{f\cdot u} \over {u-f}}}
–°–Ľ–Ķ–ī—É–Ķ—ā –ĺ—ā–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ –∑–Ĺ–į–ļ–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ
u
{\displaystyle u}
v
{\displaystyle v}
f
{\displaystyle f}
–ľ–Ĺ–ł–ľ—č–Ļ ‚ÄĒ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ī–ĺ –Ĺ–Ķ–≥–ĺ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ķ—Ā–Ľ–ł –Ľ–ł–Ĺ–∑–į —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–į—Ź ‚ÄĒ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ.
–ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź —á—Ď—Ä–Ĺ—č—Ö –Ī—É–ļ–≤ —á–Ķ—Ä–Ķ–∑ —ā–ĺ–Ĺ–ļ—É—é –≤—č–Ņ—É–ļ–Ľ—É—é –Ľ–ł–Ĺ–∑—É —Ā —Ą–ĺ–ļ—É—Ā–Ĺ—č–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ f (–ļ—Ä–į—Ā–Ĺ—č–ľ —Ü–≤–Ķ—ā–ĺ–ľ). –ü–ĺ–ļ–į–∑–į–Ĺ—č –Ľ—É—á–ł –ī–Ľ—Ź –Ī—É–ļ–≤ E, I –ł K (—Ā–ł–Ĺ–ł–ľ, –∑–Ķ–Ľ—Ď–Ĺ—č–ľ –ł –ĺ—Ä–į–Ĺ–∂–Ķ–≤—č–ľ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ). –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ī—É–ļ–≤—č E (–Ĺ–į—Ö–ĺ–ī—Ź—Č–Ķ–Ļ—Ā—Ź –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł 2f ) –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ –ł –Ņ–Ķ—Ä–Ķ–≤–Ķ—Ä–Ĺ—É—ā–ĺ–Ķ, —ā–į–ļ–ĺ–≥–ĺ –∂–Ķ —Ä–į–∑–ľ–Ķ—Ä–į. –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ I (–Ĺ–į f ) ‚ÄĒ –≤ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł. –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ö (–Ĺ–į f /2) –ľ–Ĺ–ł–ľ–ĺ–Ķ, –Ņ—Ä—Ź–ľ–ĺ–Ķ, —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –≤ 2 —Ä–į–∑–į
–õ–ł–Ĺ–Ķ–Ļ–Ĺ—č–ľ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ–ľ
m
=
a
2
b
2
a
b
{\displaystyle m={{a_{2}b_{2}} \over {ab}}}
m
=
a
2
b
2
a
b
=
v
u
{\displaystyle m={{a_{2}b_{2}} \over {ab}}={v \over u}}
v
{\displaystyle v}
u
{\displaystyle u}
–ó–ī–Ķ—Ā—Ć
m
{\displaystyle m}
–í –Ņ—Ä–į–ļ—ā–ł–ļ–Ķ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł–Ļ –≥–ĺ—Ä–į–∑–ī–ĺ —É–ī–ĺ–Ī–Ĺ–Ķ–Ķ —ć—ā–ĺ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –≤—č—Ä–į–∂–į—ā—Ć –≤ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö
u
{\displaystyle u}
f
{\displaystyle f}
f
{\displaystyle f}
m
=
f
u
− ‚ąí -->
f
;
m
=
v
− ‚ąí -->
f
f
{\displaystyle m={f \over {u-f}};\ m={{v-f} \over f}}
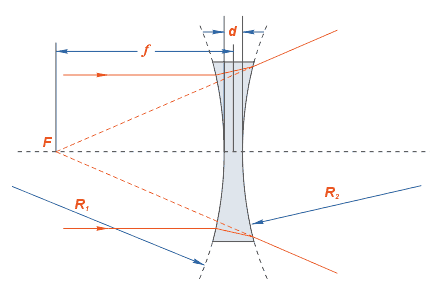
–ó–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ī–Ľ—Ź –Ľ–ł–Ĺ–∑—č –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į—Ā—Ā—á–ł—ā–į–Ĺ–ĺ –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
n
0
f
=
(
n
− ‚ąí -->
n
0
)
{
1
R
1
− ‚ąí -->
1
R
2
+
(
n
− ‚ąí -->
n
0
)
d
n
R
1
R
2
}
{\displaystyle {\frac {n_{0}}{f}}=(n-n_{0})\left\{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-n_{0})d}{nR_{1}R_{2}}}\right\}}
n
{\displaystyle n}
–Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź –ľ–į—ā–Ķ—Ä–ł–į–Ľ–į –Ľ–ł–Ĺ–∑—č,
n
0
{\displaystyle n_{0}}
d
{\displaystyle d}
–ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ—Ā–ł , —ā–į–ļ–∂–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–Ķ –ļ–į–ļ —ā–ĺ–Ľ—Č–ł–Ĺ–į –Ľ–ł–Ĺ–∑—č ,
R
1
{\displaystyle R_{1}}
R
2
{\displaystyle R_{2}}
–Ē–Ľ—Ź
R
1
{\displaystyle R_{1}}
R
2
{\displaystyle R_{2}}
d
{\displaystyle d}
—ā–ĺ–Ĺ–ļ–ĺ–Ļ , –ł –Ķ—Ď —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł –ļ–į–ļ:
n
0
f
=
(
n
− ‚ąí -->
n
0
)
{
1
R
1
− ‚ąí -->
1
R
2
}
.
{\displaystyle {\frac {n_{0}}{f}}=(n-n_{0})\left\{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right\}.}
–≠—ā—É —Ą–ĺ—Ä–ľ—É–Ľ—É —ā–į–ļ–∂–Ķ –Ĺ–į–∑—č–≤–į—é—ā —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ —ą–Ľ–ł—Ą–ĺ–≤—Č–ł–ļ–į –Ľ–ł–Ĺ–∑ . –í–Ķ–Ľ–ł—á–ł–Ĺ–į —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–į –ī–Ľ—Ź —Ā–ĺ–Ī–ł—Ä–į—é—Č–ł—Ö –Ľ–ł–Ĺ–∑, –ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–į –ī–Ľ—Ź —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–ł—Ö. –í–Ķ–Ľ–ł—á–ł–Ĺ–į
n
0
f
{\displaystyle {\frac {n_{0}}{f}}}
–ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł–Ľ–ĺ–Ļ ‚ąí1 . –ě–Ņ—ā–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł–Ľ–į —ā–į–ļ–∂–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ź –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī—č
n
0
{\displaystyle n_{0}}
–£–ļ–į–∑–į–Ĺ–Ĺ—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ—č –į–ļ–ļ—É—Ä–į—ā–Ĺ—č–ľ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł–Ķ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –≤ –Ľ–ł–Ĺ–∑–Ķ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –∑–į–ļ–ĺ–Ĺ–į –°–Ĺ–Ķ–Ľ–Ľ–į , –Ķ—Ā–Ľ–ł –Ņ–Ķ—Ä–Ķ–Ļ—ā–ł –ĺ—ā –ĺ–Ī—Č–ł—Ö —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą–ĺ—Ä–ľ—É–Ľ –ļ –Ņ–į—Ä–į–ļ—Ā–ł–į–Ľ—Ć–Ĺ–ĺ–ľ—É –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–ł—é . –ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, –ī–Ľ—Ź –≤—č–≤–ĺ–ī–į —Ą–ĺ—Ä–ľ—É–Ľ—č —ā–ĺ–Ĺ–ļ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č —É–ī–ĺ–Ī–Ĺ–ĺ –∑–į–ľ–Ķ–Ĺ–ł—ā—Ć –Ķ—Ď —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ł–∑–ľ–ĺ–Ļ –ł –∑–į—ā–Ķ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —Ą–ĺ—Ä–ľ—É–Ľ—É —É–≥–Ľ–į –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–Ļ –Ņ—Ä–ł–∑–ľ—č[ 23]
–õ–ł–Ĺ–∑—č —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č, —ā–ĺ –Ķ—Ā—ā—Ć –ĺ–Ĺ–ł –ł–ľ–Ķ—é—ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–Ķ —Ą–ĺ–ļ—É—Ā–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ—ā–į ‚ÄĒ —Ā–Ľ–Ķ–≤–į –ł–Ľ–ł —Ā–Ņ—Ä–į–≤–į, —á—ā–ĺ, –ĺ–ī–Ĺ–į–ļ–ĺ, –Ĺ–Ķ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –ļ –ī—Ä—É–≥–ł–ľ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į–ľ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –į–Ī–Ķ—Ä—Ä–į—Ü–ł—Ź–ľ , –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č—Ö –∑–į–≤–ł—Ā–ł—ā –ĺ—ā —ā–ĺ–≥–ĺ, –ļ–į–ļ–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ –Ľ–ł–Ĺ–∑–į –Ņ–ĺ–≤—Ď—Ä–Ĺ—É—ā–į –ļ —Ā–≤–Ķ—ā—É.
–õ–ł–Ĺ–∑—č –ľ–ĺ–≥—É—ā –ļ–ĺ–ľ–Ī–ł–Ĺ–ł—Ä–ĺ–≤–į—ā—Ć—Ā—Ź –ī—Ä—É–≥ —Ā –ī—Ä—É–≥–ĺ–ľ –ī–Ľ—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź —Ā–Ľ–ĺ–∂–Ĺ—č—Ö –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ. –ě–Ņ—ā–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł–Ľ–į —Ā–ł—Ā—ā–Ķ–ľ—č –ł–∑ –ī–≤—É—Ö –Ľ–ł–Ĺ–∑ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ĺ–į–Ļ–ī–Ķ–Ĺ–į –ļ–į–ļ –Ņ—Ä–ĺ—Ā—ā–į—Ź —Ā—É–ľ–ľ–į –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł–Ľ –ļ–į–∂–ī–ĺ–Ļ –Ľ–ł–Ĺ–∑—č (–Ņ—Ä–ł —É—Ā–Ľ–ĺ–≤–ł–ł, —á—ā–ĺ –ĺ–Ī–Ķ –Ľ–ł–Ĺ–∑—č –ľ–ĺ–∂–Ĺ–ĺ —Ā—á–ł—ā–į—ā—Ć —ā–ĺ–Ĺ–ļ–ł–ľ–ł –ł –ĺ–Ĺ–ł —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ—č –≤–Ņ–Ľ–ĺ—ā–Ĺ—É—é –ī—Ä—É–≥ –ļ –ī—Ä—É–≥—É –Ĺ–į –ĺ–ī–Ĺ–ĺ–Ļ –ĺ—Ā–ł):
1
F
=
1
f
1
+
1
f
2
{\displaystyle {\frac {1}{F}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}}
–ē—Ā–Ľ–ł –Ľ–ł–Ĺ–∑—č —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ—č –Ĺ–į –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į –ł –ł—Ö –ĺ—Ā–ł —Ā–ĺ–≤–Ņ–į–ī–į—é—ā (—Ā–ł—Ā—ā–Ķ–ľ–į –ł–∑ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —á–ł—Ā–Ľ–į –Ľ–ł–Ĺ–∑, –ĺ–Ī–Ľ–į–ī–į—é—Č–ł—Ö —ā–į–ļ–ł–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ü–Ķ–Ĺ—ā—Ä–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–ĺ–Ļ), —ā–ĺ –ł—Ö –ĺ–Ī—Č—É—é –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ—É—é —Ā–ł–Ľ—É —Ā –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć—é —ā–ĺ—á–Ĺ–ĺ—Ā—ā–ł –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł –ł–∑ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź:
1
F
=
1
f
1
+
1
f
2
− ‚ąí -->
L
f
1
f
2
{\displaystyle {\frac {1}{F}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}-{\frac {L}{f_{1}f_{2}}}}
–≥–ī–Ķ
L
{\displaystyle L}
–≥–Ľ–į–≤–Ĺ—č–ľ–ł –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ź–ľ–ł –Ľ–ł–Ĺ–∑.
–í —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–ł–Ī–ĺ—Ä–į—Ö –ļ –ļ–į—á–Ķ—Ā—ā–≤—É –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī—ä—Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤—č—Ā–ĺ–ļ–ł–Ķ —ā—Ä–Ķ–Ī–ĺ–≤–į–Ĺ–ł—Ź.
–ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ, –ī–į–≤–į–Ķ–ľ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ļ –Ľ–ł–Ĺ–∑–ĺ–Ļ, –≤ —Ā–ł–Ľ—É —Ü–Ķ–Ľ–ĺ–≥–ĺ —Ä—Ź–ī–į –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ĺ–≤ –Ĺ–Ķ —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź–Ķ—ā —ć—ā–ł–ľ —ā—Ä–Ķ–Ī–ĺ–≤–į–Ĺ–ł—Ź–ľ. –£—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–į –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ĺ–≤ –ī–ĺ—Ā—ā–ł–≥–į–Ķ—ā—Ā—Ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–ľ –Ņ–ĺ–ī–Ī–ĺ—Ä–ĺ–ľ —Ä—Ź–ī–į –Ľ–ł–Ĺ–∑ –≤ —Ü–Ķ–Ĺ—ā—Ä–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—É—é –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É ‚ÄĒ –ĺ–Ī—ä–Ķ–ļ—ā–ł–≤ . –Ě–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ł –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –į–Ī–Ķ—Ä—Ä–į—Ü–ł—Ź–ľ–ł , –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ī–Ķ–Ľ—Ź—ā—Ā—Ź –Ĺ–į —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –≤–ł–ī—č:
–ü–ĺ–Ľ–ł–ľ–Ķ—Ä—č –ī–į—é—ā –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ–∑–ī–į–≤–į—ā—Ć –Ĺ–Ķ–ī–ĺ—Ä–ĺ–≥–ł–Ķ –į—Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –Ľ–ł–Ĺ–∑—č —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –Ľ–ł—ā—Ć—Ź .
–õ–ł–Ĺ–∑—č –ļ–ĺ–Ĺ—ā–į–ļ—ā–Ĺ—č–Ķ –í –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ—Ą—ā–į–Ľ—Ć–ľ–ĺ–Ľ–ĺ–≥–ł–ł —Ā–ĺ–∑–ī–į–Ĺ—č –ľ—Ź–≥–ļ–ł–Ķ –ļ–ĺ–Ĺ—ā–į–ļ—ā–Ĺ—č–Ķ –Ľ–ł–Ĺ–∑—č . –ü–Ķ—Ä–≤—č–ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ź–ľ–ł –Ľ–ł–Ĺ–∑ —ā–į–ļ–ĺ–≥–ĺ –≤–ł–ī–į —Ā—ā–į–Ľ–į –ļ–ĺ–ľ–Ņ–į–Ĺ–ł—Ź Bausch+Lomb . –ü—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–ĺ –ľ—Ź–≥–ļ–ł—Ö –Ľ–ł–Ĺ–∑ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ĺ –Ĺ–į –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–ł –ľ–į—ā–Ķ—Ä–ł–į–Ľ–ĺ–≤, –ł–ľ–Ķ—é—Č–ł—Ö –Ī–ł—Ą–į–∑–Ĺ—É—é –Ņ—Ä–ł—Ä–ĺ–ī—É, —Ā–ĺ—á–Ķ—ā–į—é—Č–ł—Ö —Ą—Ä–į–≥–ľ–Ķ–Ĺ—ā—č –ļ—Ä–Ķ–ľ–Ĺ–ł–Ļ-–ĺ—Ä–≥–į–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł–Ľ–ł –ļ—Ä–Ķ–ľ–Ĺ–ł–Ļ-—Ą—ā–ĺ—Ä–ĺ—Ä–≥–į–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ–ĺ–Ľ–ł–ľ–Ķ—Ä–į —Ā–ł–Ľ–ł–ļ–ĺ–Ĺ–į –ł –≥–ł–ī—Ä–ĺ—Ą–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–Ľ–ł–ľ–Ķ—Ä–į –≥–ł–ī—Ä–ĺ–≥–Ķ–Ľ—Ź . –†–į–Ī–ĺ—ā–į –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ –Ī–ĺ–Ľ–Ķ–Ķ 20 –Ľ–Ķ—ā –Ņ—Ä–ł–≤–Ķ–Ľ–į –ļ —Ā–ĺ–∑–ī–į–Ĺ–ł—é –≤ –ļ–ĺ–Ĺ—Ü–Ķ 1990-—Ö –≥–ĺ–ī–ĺ–≤ —Ā–ł–Ľ–ł–ļ–ĺ–Ĺ-–≥–ł–ī—Ä–ĺ–≥–Ķ–Ľ–Ķ–≤—č—Ö –Ľ–ł–Ĺ–∑ , –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ī–Ľ–į–≥–ĺ–ī–į—Ä—Ź —Ā–ĺ—á–Ķ—ā–į–Ĺ–ł—é –≥–ł–ī—Ä–ĺ—Ą–ł–Ľ—Ć–Ĺ—č—Ö —Ā–≤–ĺ–Ļ—Ā—ā–≤ –ł –≤—č—Ā–ĺ–ļ–ĺ–Ļ –ļ–ł—Ā–Ľ–ĺ—Ä–ĺ–ī–ĺ–Ņ—Ä–ĺ–Ĺ–ł—Ü–į–Ķ–ľ–ĺ—Ā—ā–ł –ľ–ĺ–≥—É—ā –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć—Ā—Ź –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ 30 –ī–Ĺ–Ķ–Ļ –ļ—Ä—É–≥–Ľ–ĺ—Ā—É—ā–ĺ—á–Ĺ–ĺ.[ 24]
–ě—Ā–Ĺ–ĺ–≤–Ĺ–į—Ź —Ā—ā–į—ā—Ć—Ź:
–ö–≤–į—Ä—Ü–Ķ–≤–ĺ–Ķ —Ā—ā–Ķ–ļ–Ľ–ĺ –ö–≤–į—Ä—Ü–Ķ–≤–ĺ–Ķ —Ā—ā–Ķ–ļ–Ľ–ĺ ‚ÄĒ –ĺ–ī–Ĺ–ĺ–ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–Ĺ–ĺ–Ķ —Ā—ā–Ķ–ļ–Ľ–ĺ , —Ā–ĺ—Ā—ā–ĺ—Ź—Č–Ķ–Ķ –ł–∑ –ī–ł–ĺ–ļ—Ā–ł–ī–į –ļ—Ä–Ķ–ľ–Ĺ–ł—Ź , —Ā –Ĺ–Ķ–∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ (–ĺ–ļ–ĺ–Ľ–ĺ 0,01 % –ł –ľ–Ķ–Ĺ—Ć—ą–Ķ) —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł–Ķ–ľ –Ņ—Ä–ł–ľ–Ķ—Ā–Ķ–Ļ Al2 –ě3 , –°–į–ě –ł MgO. –ě–Ĺ–ĺ –ĺ—ā–Ľ–ł—á–į–Ķ—ā—Ā—Ź –≤—č—Ā–ĺ–ļ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ—Ā—ā–ĺ–Ļ–ļ–ĺ—Ā—ā—Ć—é –ł –ł–Ĺ–Ķ—Ä—ā–Ĺ–ĺ—Ā—ā—Ć—é –ļ–ĺ –ľ–Ĺ–ĺ–≥–ł–ľ —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ł–ľ —Ä–Ķ–į–ļ—ā–ł–≤–į–ľ –∑–į –ł—Ā–ļ–Ľ—é—á–Ķ–Ĺ–ł–Ķ–ľ –Ņ–Ľ–į–≤–ł–ļ–ĺ–≤–ĺ–Ļ –ļ–ł—Ā–Ľ–ĺ—ā—č .
–ü—Ä–ĺ–∑—Ä–į—á–Ĺ–ĺ–Ķ –ļ–≤–į—Ä—Ü–Ķ–≤–ĺ–Ķ —Ā—ā–Ķ–ļ–Ľ–ĺ —Ö–ĺ—Ä–ĺ—ą–ĺ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā —É–Ľ—Ć—ā—Ä–į—Ą–ł–ĺ–Ľ–Ķ—ā–ĺ–≤—č–Ķ –ł –≤–ł–ī–ł–ľ—č–Ķ –Ľ—É—á–ł —Ā–≤–Ķ—ā–į .
–ö—Ä–Ķ–ľ–Ĺ–ł–Ļ —Ö–ĺ—Ä–ĺ—ą–ĺ –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā –ł–Ĺ—Ą—Ä–į–ļ—Ä–į—Ā–Ĺ–ĺ–Ķ –ł–∑–Ľ—É—á–Ķ–Ĺ–ł–Ķ —Ā –ī–Ľ–ł–Ĺ–į–ľ–ł –≤–ĺ–Ľ–Ĺ –ĺ—ā 1 –ī–ĺ 9 –ľ–ļ–ľ, –ł–ľ–Ķ–Ķ—ā –Ī–ĺ–Ľ—Ć—ą–ĺ–Ļ –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź (n = 3,42 –Ņ—Ä–ł
λ őĽ -->
{\displaystyle \lambda }
[ 25]
–ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –ļ—Ä–Ķ–ľ–Ĺ–ł—Ź –ł —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł–ł –Ķ–≥–ĺ –ĺ–Ī—Ä–į–Ī–ĺ—ā–ļ–ł –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—ā —Ā–ĺ–∑–ī–į—ā—Ć –Ľ–ł–Ĺ–∑—č –ī–Ľ—Ź —Ä–Ķ–Ĺ—ā–≥–Ķ–Ĺ–ĺ–≤—Ā–ļ–ĺ–≥–ĺ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–į —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–ľ–į–≥–Ĺ–ł—ā–Ĺ—č—Ö –≤–ĺ–Ľ–Ĺ[ 26]
–ü—É—ā—Ď–ľ –Ĺ–į–Ĺ–Ķ—Ā–Ķ–Ĺ–ł—Ź –Ĺ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć –Ľ–ł–Ĺ–∑—č –ľ–Ĺ–ĺ–≥–ĺ—Ā–Ľ–ĺ–Ļ–Ĺ—č—Ö –ī–ł—ć–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ–ĺ–ļ—Ä—č—ā–ł–Ļ –ľ–ĺ–∂–Ĺ–ĺ –ī–ĺ–Ī–ł—ā—Ć—Ā—Ź –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł—Ź –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ—ā–į –ł, –≤—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ —ć—ā–ĺ–≥–ĺ, —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—Ź –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–į–Ĺ–ł—Ź . –Ę–į–ļ–ł–Ķ –Ľ–ł–Ĺ–∑—č –Ľ–Ķ–≥–ļ–ĺ —É–∑–Ĺ–į—ā—Ć –Ņ–ĺ —Ą–ł–ĺ–Ľ–Ķ—ā–ĺ–≤—č–ľ –Ī–Ľ–ł–ļ–į–ľ: –ĺ–Ĺ–ł –Ĺ–Ķ –ĺ—ā—Ä–į–∂–į—é—ā –∑–Ķ–Ľ—Ď–Ĺ—č–Ļ —Ü–≤–Ķ—ā, –ĺ—ā—Ä–į–∂–į—Ź –ļ—Ä–į—Ā–Ĺ—č–Ļ –ł —Ā–ł–Ĺ–ł–Ļ, —á—ā–ĺ –≤ —Ā—É–ľ–ľ–Ķ –ī–į—Ď—ā —Ą–ł–ĺ–Ľ–Ķ—ā–ĺ–≤—č–Ļ. –ü–ĺ–ī–į–≤–Ľ—Ź—é—Č–Ķ–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–ĺ –Ľ–ł–Ĺ–∑ –ī–Ľ—Ź —Ą–ĺ—ā–ĺ—ā–Ķ—Ö–Ĺ–ł–ļ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į –°–°–°–†, –≤ —ā–ĺ–ľ —á–ł—Ā–Ľ–Ķ –ī–Ľ—Ź –Ī—č—ā–ĺ–≤—č—Ö –ĺ–Ī—ä–Ķ–ļ—ā–ł–≤–ĺ–≤, –ł–∑–≥–ĺ—ā–į–≤–Ľ–ł–≤–į–Ľ–ĺ—Ā—Ć –Ņ—Ä–ĺ—Ā–≤–Ķ—ā–Ľ—Ď–Ĺ–Ĺ—č–ľ–ł.
–õ–ł–Ĺ–∑—č —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —ą–ł—Ä–ĺ–ļ–ĺ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ď–Ĺ–Ĺ—č–ľ –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł–ľ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–ľ –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–į –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ .
–Ę—Ä–į–ī–ł—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –Ľ–ł–Ĺ–∑ ‚ÄĒ –Ī–ł–Ĺ–ĺ–ļ–Ľ–ł , —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ—č , –ĺ–Ņ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ—Ä–ł—Ü–Ķ–Ľ—č , —ā–Ķ–ĺ–ī–ĺ–Ľ–ł—ā—č , –ľ–ł–ļ—Ä–ĺ—Ā–ļ–ĺ–Ņ—č , —Ą–ĺ—ā–ĺ- –ł –≤–ł–ī–Ķ–ĺ—ā–Ķ—Ö–Ĺ–ł–ļ–į . –ě–ī–ł–Ĺ–ĺ—á–Ĺ—č–Ķ —Ā–ĺ–Ī–ł—Ä–į—é—Č–ł–Ķ –Ľ–ł–Ĺ–∑—č –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ļ–į–ļ —É–≤–Ķ–Ľ–ł—á–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ā—ā—Ď–ļ–Ľ–į .
–Ē—Ä—É–≥–į—Ź –≤–į–∂–Ĺ–į—Ź —Ā—Ą–Ķ—Ä–į –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ľ–ł–Ĺ–∑ ‚ÄĒ –ĺ—Ą—ā–į–Ľ—Ć–ľ–ĺ–Ľ–ĺ–≥–ł—Ź , –≥–ī–Ķ –Ī–Ķ–∑ –Ĺ–ł—Ö –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –ł—Ā–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ĺ–≤ –∑—Ä–Ķ–Ĺ–ł—Ź ‚ÄĒ –Ī–Ľ–ł–∑–ĺ—Ä—É–ļ–ĺ—Ā—ā–ł , –ī–į–Ľ—Ć–Ĺ–ĺ–∑–ĺ—Ä–ļ–ĺ—Ā—ā–ł , –Ĺ–Ķ–Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–Ļ –į–ļ–ļ–ĺ–ľ–ĺ–ī–į—Ü–ł–ł , –į—Ā—ā–ł–≥–ľ–į—ā–ł–∑–ľ–į –ł –ī—Ä—É–≥–ł—Ö –∑–į–Ī–ĺ–Ľ–Ķ–≤–į–Ĺ–ł–Ļ. –õ–ł–Ĺ–∑—č –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā –≤ —ā–į–ļ–ł—Ö –Ņ—Ä–ł—Ā–Ņ–ĺ—Ā–ĺ–Ī–Ľ–Ķ–Ĺ–ł—Ź—Ö, –ļ–į–ļ –ĺ—á–ļ–ł –ł –ļ–ĺ–Ĺ—ā–į–ļ—ā–Ĺ—č–Ķ –Ľ–ł–Ĺ–∑—č . –Ę–į–ļ–∂–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ–ĺ–ī–≤–ł–ī –Ľ–ł–Ĺ–∑, –Ĺ–ĺ—á–Ĺ—č–Ķ –Ľ–ł–Ĺ–∑—č . –ě–Ĺ–ł –ł–ľ–Ķ—é—ā –Ī–ĺ–Ľ–Ķ–Ķ –∂–Ķ—Ā—ā–ļ—É—é –ĺ—Ā–Ĺ–ĺ–≤—É –ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ł—Ā–ļ–Ľ—é—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤–ĺ –≤—Ä–Ķ–ľ—Ź —Ā–Ĺ–į, –ī–Ľ—Ź –≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ļ–ĺ—Ä—Ä–Ķ–ļ—Ü–ł–ł –∑—Ä–Ķ–Ĺ–ł—Ź –≤ –ī–Ĺ–Ķ–≤–Ĺ–ĺ–Ķ –≤—Ä–Ķ–ľ—Ź.
–í —Ä–į–ī–ł–ĺ–į—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ–ł–ł –ł —Ä–į–ī–į—Ä–į—Ö —á–į—Ā—ā–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ī–ł—ć–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –Ľ–ł–Ĺ–∑—č, —Ā–ĺ–Ī–ł—Ä–į—é—Č–ł–Ķ –Ņ–ĺ—ā–ĺ–ļ —Ä–į–ī–ł–ĺ–≤–ĺ–Ľ–Ĺ –≤ –Ņ—Ä–ł—Ď–ľ–Ĺ—É—é –į–Ĺ—ā–Ķ–Ĺ–Ĺ—É , –Ľ–ł–Ī–ĺ —Ą–ĺ–ļ—É—Ā–ł—Ä—É—é—Č–ł–Ķ –ł—Ö –Ĺ–į —Ü–Ķ–Ľ–ł.
–í –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł–ł –Ņ–Ľ—É—ā–ĺ–Ĺ–ł–Ķ–≤—č—Ö —Ź–ī–Ķ—Ä–Ĺ—č—Ö –Ī–ĺ–ľ–Ī –ī–Ľ—Ź –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–į—Ā—Ö–ĺ–ī—Ź—Č–Ķ–Ļ—Ā—Ź —É–ī–į—Ä–Ĺ–ĺ–Ļ –≤–ĺ–Ľ–Ĺ—č –ĺ—ā —ā–ĺ—á–Ķ—á–Ĺ–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į (–ī–Ķ—ā–ĺ–Ĺ–į—ā–ĺ—Ä–į ) –≤ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ—É—é —Ā—Ö–ĺ–ī—Ź—Č—É—é—Ā—Ź, –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź–Ľ–ł—Ā—Ć –Ľ–ł–Ĺ–∑–ĺ–≤—č–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č, –ł–∑–≥–ĺ—ā–ĺ–≤–Ľ–Ķ–Ĺ–Ĺ—č–Ķ –ł–∑ –≤–∑—Ä—č–≤—á–į—ā–ļ–ł —Ā —Ä–į–∑–Ĺ–ĺ–Ļ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć—é –ī–Ķ—ā–ĺ–Ĺ–į—Ü–ł–ł (—ā–ĺ –Ķ—Ā—ā—Ć —Ā —Ä–į–∑–Ĺ—č–ľ –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–ľ –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź).
‚ÜĎ –ź–Ĺ–į–Ĺ—Ć–Ķ–≤ –ģ. –ź. –õ–ł–Ĺ–∑–į –§–ł–∑–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź / –ď–Ľ. —Ä–Ķ–ī. –ź. –ú. –ü—Ä–ĺ—Ö–ĺ—Ä–ĺ–≤ . ‚ÄĒ –ú. : –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź , 1990. ‚ÄĒ –Ę. 2. ‚ÄĒ –°. 591‚ÄĒ592. ‚ÄĒ 704 —Ā. ‚ÄĒ 100 000 —ć–ļ–∑. ‚ÄĒ ISBN 5-85270-061-4 .‚ÜĎ The variant spelling lense is sometimes seen. While it is listed as an alternative spelling in some dictionaries, most mainstream dictionaries do not list it as acceptable.
‚ÜĎ Sines, George (1987). "Lenses in antiquity" . American Journal of Archaeology . 91 (2): 191‚Äď 196. doi :10.2307/505216 . ‚ÜĎ Whitehouse, David (1 –ł—é–Ľ—Ź 1999). "World's oldest telescope?" . BBC News . –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 1 —Ą–Ķ–≤—Ä–į–Ľ—Ź 2009. –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 10 –ľ–į—Ź 2008 . ‚ÜĎ The Nimrud lens/The Layard lens (–Ĺ–Ķ–ĺ–Ņ—Ä.) . Collection database . The British Museum. –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 25 –Ĺ–ĺ—Ź–Ī—Ä—Ź 2012. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 19 –ĺ–ļ—ā—Ź–Ī—Ä—Ź 2012 –≥–ĺ–ī–į.‚ÜĎ D. Brewster. On an account of a rock-crystal lens and decomposed glass found in Niniveh // Die Fortschritte der Physik : [–Ĺ–Ķ–ľ. ‚ÜĎ Kriss, Timothy C. (April 1998). "History of the Operating Microscope: From Magnifying Glass to Microneurosurgery". Neurosurgery . 42 (4): 899‚Äď 907. doi :10.1097/00006123-199804000-00116 . PMID 9574655 . ‚ÜĎ Aristophanes .‚ÜĎ Pliny the Elder , The Natural History (trans. John Bostock) Book XXXVII, Chap. 10 –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 4 –ĺ–ļ—ā—Ź–Ī—Ä—Ź 2008 –Ĺ–į Wayback Machine .‚ÜĎ Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 16 –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 28 —Ā–Ķ–Ĺ—ā—Ź–Ī—Ä—Ź 2008 –Ĺ–į Wayback Machine
‚ÜĎ Tilton, Buck. The Complete Book of Fire: Building Campfires for Warmth, Light, Cooking, and Survival . ‚ÄĒ Menasha Ridge Press, 2005. ‚ÄĒ P. 25. ‚ÄĒ ISBN 978-0-89732-633-9 .‚ÜĎ Glick, Thomas F. Medieval science, technology, and medicine: an encyclopedia . ‚ÄĒ Routledge, 2005. ‚ÄĒ P. 167. ‚ÄĒ ISBN 978-0-415-96930-7 .–ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 20 —Ź–Ĺ–≤–į—Ä—Ź 2023 –Ĺ–į Wayback Machine ‚ÜĎ Al Van Helden. The Galileo Project > Science > The Telescope –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 3 –į–≤–≥—É—Ā—ā–į 2017 –Ĺ–į Wayback Machine . Galileo.rice.edu. Retrieved on 6 June 2012.
‚ÜĎ Henry C. King. The History of the Telescope . ‚ÄĒ Courier Dover Publications. ‚ÄĒ P. 27. ‚ÄĒ ISBN 978-0-486-43265-6 .–ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 2 –ł—é–Ľ—Ź 2023 –Ĺ–į Wayback Machine ‚ÜĎ Paul S. Agutter. Thinking about Life: The History and Philosophy of Biology and Other Sciences . ‚ÄĒ Springer. ‚ÄĒ P. 17. ‚ÄĒ ISBN 978-1-4020-8865-0 .‚ÜĎ Vincent Ilardi. Renaissance Vision from Spectacles to Telescopes . ‚ÄĒ American Philosophical Society, 2007. ‚ÄĒ P. 210. ‚ÄĒ ISBN 978-0-87169-259-7 .‚ÜĎ Microscopes: Time Line –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 9 —Ź–Ĺ–≤–į—Ä—Ź 2010 –Ĺ–į Wayback Machine , Nobel Foundation. Retrieved 3 April 2009‚ÜĎ Fred Watson. Stargazer: The Life and Times of the Telescope . ‚ÄĒ Allen & Unwin. ‚ÄĒ P. 55. ‚ÄĒ ISBN 978-1-74175-383-7 .‚ÜĎ This paragraph is adapted from the 1888 edition of the Encyclop√¶dia Britannica.
‚ÜĎ –•–ĺ–ī –Ľ—É—á–Ķ–Ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ, –ļ–į–ļ –≤ –ł–ī–Ķ–į–Ľ–ł–∑–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ (—ā–ĺ–Ĺ–ļ–ĺ–Ļ) –Ľ–ł–Ĺ–∑–Ķ, –Ī–Ķ–∑ —É–ļ–į–∑–į–Ĺ–ł—Ź –Ĺ–į –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į —Ä–Ķ–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä–į–Ĺ–ł—Ü–Ķ —Ä–į–∑–ī–Ķ–Ľ–į —Ā—Ä–Ķ–ī. –Ē–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–ĺ–ļ–į–∑–į–Ĺ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —É—ā—Ä–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č–Ļ –ĺ–Ī—Ä–į–∑ –ī–≤–ĺ—Ź–ļ–ĺ–≤—č–Ņ—É–ļ–Ľ–ĺ–Ļ –Ľ–ł–Ĺ–∑—č.
‚ÜĎ –•–Ķ–Ĺ–ī–Ķ–Ľ—Ć –ź. –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –∑–į–ļ–ĺ–Ĺ—č —Ą–ł–∑–ł–ļ–ł. ‚ÄĒ –ú.: –§–ł–∑–ľ–į—ā–≥–ł–∑, 1959. ‚ÄĒ 284 —Ā. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 21 —Ź–Ĺ–≤–į—Ä—Ź 2015 –≥–ĺ–ī–į.
‚ÜĎ [psychology_pedagogy.academic.ru/14495/–†–ź–°–°–Ę–ě–Į–Ě–ė–ē_–Ě–ź–ė–õ–£–ß–®–ē–ď–ě_–ó–†–ē–Ě–ė–Į –†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ĺ–į–ł–Ľ—É—á—ą–Ķ–≥–ĺ –∑—Ä–Ķ–Ĺ–ł—Ź –Ĺ–į academic.ru]
‚ÜĎ –õ–į–Ĺ–ī—Ā–Ī–Ķ—Ä–≥ –ď.–°. ¬ß88. –ü—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł–Ķ –≤ –Ľ–ł–Ĺ–∑–Ķ. –§–ĺ–ļ—É—Ā—č –Ľ–ł–Ĺ–∑—č // –≠–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č–Ļ —É—á–Ķ–Ī–Ĺ–ł–ļ —Ą–ł–∑–ł–ļ–ł. ‚ÄĒ 13-–Ķ –ł–∑–ī. ‚ÄĒ –ú. : –§–ł–∑–ľ–į—ā–Ľ–ł—ā , 2003. ‚ÄĒ –Ę. 3. –ö–ĺ–Ľ–Ķ–Ī–į–Ĺ–ł—Ź –ł –≤–ĺ–Ľ–Ĺ—č. –ě–Ņ—ā–ł–ļ–į. –ź—ā–ĺ–ľ–Ĺ–į—Ź –ł —Ź–ī–Ķ—Ä–Ĺ–į—Ź —Ą–ł–∑–ł–ļ–į. ‚ÄĒ –°. 236‚ÄĒ242. ‚ÄĒ 656 —Ā. ‚ÄĒ ISBN 5922103512 .‚ÜĎ –Ě–į—É–ļ–į –≤ –°–ł–Ī–ł—Ä–ł (–Ĺ–Ķ–ĺ–Ņ—Ä.) . –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 15 –Ĺ–ĺ—Ź–Ī—Ä—Ź 2007. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 20 —Ź–Ĺ–≤–į—Ä—Ź 2009 –≥–ĺ–ī–į.‚ÜĎ –§–ł–∑–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź. –í 5-—ā–ł —ā–ĺ–ľ–į—Ö. / –ź. –ú. –ü—Ä–ĺ—Ö–ĺ—Ä–ĺ–≤. ‚ÄĒ –ú. : –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 1988. ‚ÜĎ –ź—Ä–ł—Ā—ā–ĺ–≤ –í. –í., –®–į–Ī–Ķ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ –õ. –ď. –°–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ –ī–ĺ—Ā—ā–ł–∂–Ķ–Ĺ–ł—Ź —Ä–Ķ–Ĺ—ā–≥–Ķ–Ĺ–ĺ–≤—Ā–ļ–ĺ–Ļ –ĺ–Ņ—ā–ł–ļ–ł –Ņ—Ä–Ķ–Ľ–ĺ–ľ–Ľ–Ķ–Ĺ–ł—Ź // –£–§–Ě. ‚ÄĒ 2008. ‚ÄĒ –Ę. 178 . ‚ÄĒ –°. 61‚Äď83 . ‚ÄĒ doi :10.3367/UFNr.0178.200801c.0061 .
–ö—Ä–į—ā–ļ–ł–Ļ —Ą–ĺ—ā–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ / –ü–ĺ–ī –ĺ–Ī—Č–Ķ–Ļ —Ä–Ķ–ī–į–ļ—Ü–ł–Ķ–Ļ –ī.—ā.–Ĺ. –í. –í. –ü—É—Ā—Ć–ļ–ĺ–≤–į. ‚ÄĒ 2-–Ķ –ł–∑–ī. ‚ÄĒ –ú. : –ė—Ā–ļ—É—Ā—Ā—ā–≤–ĺ, 1953. –õ–į–Ĺ–ī—Ā–Ī–Ķ—Ä–≥ –ď. –°. –ú. : –Ě–į—É–ļ–į, 1976.–ü–ĺ–Ľ–ł—ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–Ľ–ĺ–≤–į—Ä—Ć / –≥–Ľ–į–≤. —Ä–Ķ–ī. –ź. –ģ. –ė—ą–Ľ–ł–Ĺ—Ā–ļ–ł–Ļ . ‚ÄĒ 3-–Ķ –ł–∑–ī. ‚ÄĒ –ú. : –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź –≠–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 1989. –õ–ł–Ĺ–∑–į // –§–ĺ—ā–ĺ–ļ–ł–Ĺ–ĺ—ā–Ķ—Ö–Ĺ–ł–ļ–į: –≠–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź / –ď–Ľ. —Ä–Ķ–ī. –ē. –ź. –ė–ĺ—Ą–ł—Ā . ‚ÄĒ –ú. : –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź , 1981. ‚ÄĒ 447 —Ā.
–Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ
–≤–Ĺ–Ķ—ą–Ĺ–ł–Ķ —Ā—Ā—č–Ľ–ļ–ł –≤ —ć—ā–ĺ–Ļ —Ā—ā–į—ā—Ć–Ķ
–≤–Ķ–ī—É—ā –Ĺ–į —Ā–į–Ļ—ā—č, –∑–į–Ĺ–Ķ—Ā—Ď–Ĺ–Ĺ—č–Ķ –≤ —Ā–Ņ–į–ľ-–Ľ–ł—Ā—ā –≠—ā–ł —Ā–į–Ļ—ā—č –ľ–ĺ–≥—É—ā –Ĺ–į—Ä—É—ą–į—ā—Ć –į–≤—ā–ĺ—Ä—Ā–ļ–ł–Ķ –Ņ—Ä–į–≤–į, –Ī—č—ā—Ć –Ņ—Ä–ł–∑–Ĺ–į–Ĺ—č –Ĺ–Ķ–į–≤—ā–ĺ—Ä–ł—ā–Ķ—ā–Ĺ—č–ľ–ł –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į–ľ–ł –ł–Ľ–ł –Ņ–ĺ –ī—Ä—É–≥–ł–ľ –Ņ—Ä–ł—á–ł–Ĺ–į–ľ –Ī—č—ā—Ć –∑–į–Ņ—Ä–Ķ—Č–Ķ–Ĺ—č –≤ –í–ł–ļ–ł–Ņ–Ķ–ī–ł–ł. –†–Ķ–ī–į–ļ—ā–ĺ—Ä–į–ľ —Ā–Ľ–Ķ–ī—É–Ķ—ā –∑–į–ľ–Ķ–Ĺ–ł—ā—Ć —ā–į–ļ–ł–Ķ —Ā—Ā—č–Ľ–ļ–ł —Ā—Ā—č–Ľ–ļ–į–ľ–ł –Ĺ–į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ķ –Ņ—Ä–į–≤–ł–Ľ–į–ľ —Ā–į–Ļ—ā—č –ł–Ľ–ł –Ī–ł–Ī–Ľ–ł–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–ľ–ł —Ā—Ā—č–Ľ–ļ–į–ľ–ł –Ĺ–į –Ņ–Ķ—á–į—ā–Ĺ—č–Ķ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ł –Ľ–ł–Ī–ĺ —É–ī–į–Ľ–ł—ā—Ć –ł—Ö (–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, –≤–ľ–Ķ—Ā—ā–Ķ —Ā –Ņ–ĺ–ī—ā–≤–Ķ—Ä–∂–ī–į–Ķ–ľ—č–ľ –ł–ľ–ł —Ā–ĺ–ī–Ķ—Ä–∂–ł–ľ—č–ľ).
–°–Ņ–ł—Ā–ĺ–ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–Ĺ—č—Ö —Ā—Ā—č–Ľ–ĺ–ļ
psychology_pedagogy.academic.ru