–ó–į–ī–į—á–į –ĺ —Ä–į–∑–ĺ—Ä–Ķ–Ĺ–ł–ł –ł–≥—Ä–ĺ–ļ–į ‚ÄĒ –∑–į–ī–į—á–į –ł–∑ –ĺ–Ī–Ľ–į—Ā—ā–ł —ā–Ķ–ĺ—Ä–ł–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ķ–Ļ .
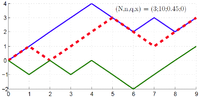
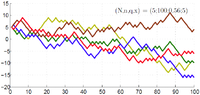
–Ę—Ä–į–Ķ–ļ—ā–ĺ—Ä–ł–ł —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ–Ļ –ł–≥—Ä—č –ī–Ľ–ł–Ĺ–ĺ—é 1000 —ą–į–≥–ĺ–≤; –ļ–ĺ—Ä–ł–ī–ĺ—Ä –Ī–Ľ—É–∂–ī–į–Ĺ–ł—Ź —á–į—Ā—ā–ł—Ü—č –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ –≥–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ—Ć–Ĺ—č–ľ–ł –Ľ–ł–Ĺ–ł—Ź–ľ–ł
–ó–į —Ā—ā–ĺ–Ľ–ĺ–ľ —Ā–ł–ī—Ź—ā –ī–≤–į –ł–≥—Ä–ĺ–ļ–į . –£ –Ņ–Ķ—Ä–≤–ĺ–≥–ĺ –≤ —Ä–į—Ā–Ņ–ĺ—Ä—Ź–∂–Ķ–Ĺ–ł–ł –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź
− ‚ąí -->
A
(
A
<
0
,
− ‚ąí -->
A
>
0
)
{\displaystyle -A\ (A<0,-A>0)}
B
(
B
>
0
)
{\displaystyle B\ (B>0)}
–≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć , —á—ā–ĺ –≤—č–Ņ–į–ī–Ķ—ā –į–≤–Ķ—Ä—Ā , –ľ–ĺ–∂–Ķ—ā —Ä–į–≤–Ĺ—Ź—ā—Ć—Ā—Ź –Ľ—é–Ī–ĺ–ľ—É —á–ł—Ā–Ľ—É –ĺ—ā 0 –ī–ĺ 1 –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ). –ē—Ā–Ľ–ł –Ĺ–į –ľ–ĺ–Ĺ–Ķ—ā–Ķ –≤—č–Ņ–į–ī–į–Ķ—ā –į–≤–Ķ—Ä—Ā, —ā–ĺ —Ä—É–Ī–Ľ—Ć –≤—č–ł–≥—Ä—č–≤–į–Ķ—ā –Ņ–Ķ—Ä–≤—č–Ļ –ł–≥—Ä–ĺ–ļ (–≤—ā–ĺ—Ä–ĺ–Ļ –ł–≥—Ä–ĺ–ļ –≤—č–Ņ–Ľ–į—á–ł–≤–į–Ķ—ā –Ņ–Ķ—Ä–≤–ĺ–ľ—É 1 —Ä—É–Ī–Ľ—Ć), –į –Ķ—Ā–Ľ–ł –≤—č–Ņ–į–ī–į–Ķ—ā —Ä–Ķ–≤–Ķ—Ä—Ā, —ā–ĺ –Ņ–Ķ—Ä–≤—č–Ļ –ł–≥—Ä–ĺ–ļ –Ņ–Ľ–į—ā–ł—ā –≤—ā–ĺ—Ä–ĺ–ľ—É –ĺ–ī–ł–Ĺ —Ä—É–Ī–Ľ—Ć. –Ę—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć —ā–ĺ–≥–ĺ, —á—ā–ĺ –ĺ–ī–ł–Ĺ –ł–∑ –ł–≥—Ä–ĺ–ļ–ĺ–≤ –Ņ—Ä–ĺ–ł–≥—Ä–į–Ķ—ā—Ā—Ź –≤ –Ĺ–ĺ–Ľ—Ć –∑–į
n
{\displaystyle n}
–Ē–į–Ĺ–Ĺ–į—Ź —Ā–ł—ā—É–į—Ü–ł—Ź –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ā–ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ: –ł–ľ–Ķ–Ķ—ā—Ā—Ź –Ī–Ľ—É–∂–ī–į—é—Č–į—Ź —á–į—Ā—ā–ł—Ü–į –ł –ļ–ĺ—Ä–ł–ī–ĺ—Ä
[
A
;
B
]
{\displaystyle [A;B]}
n
{\displaystyle n}
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā—Ö–Ķ–ľ—É –Ď–Ķ—Ä–Ĺ—É–Ľ–Ľ–ł —Ā
n
{\displaystyle n}
–ü—É—Ā—ā—Ć
(
Ω ő© -->
,
A
,
P
)
{\displaystyle (\Omega ,{\mathcal {A}},\mathbb {P} )}
Ω ő© -->
=
{
ω ŌČ -->
: : -->
ω ŌČ -->
=
(
x
1
;
… ‚Ķ -->
;
x
n
)
,
x
i
=
± ¬Ī -->
1
}
{\displaystyle \Omega ={\bigl \{}\omega \colon \omega =(x_{1};\ldots ;x_{n}),\ x_{i}=\pm 1{\bigr \}}}
A
=
{
A
i
⊆ ‚äÜ -->
Ω ő© -->
}
{\displaystyle {\mathcal {A}}=\{A_{i}\subseteq \Omega \}}
–į–Ľ–≥–Ķ–Ī—Ä–į –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į ,
P
(
{
ω ŌČ -->
}
)
=
p
ν őĹ -->
(
ω ŌČ -->
)
⋅ ‚čÖ -->
q
n
− ‚ąí -->
ν őĹ -->
(
ω ŌČ -->
)
{\displaystyle \mathbb {P} {\bigl (}\{\omega \}{\bigr )}=p^{\nu (\omega )}\cdot q^{n-\nu (\omega )}}
ν őĹ -->
(
ω ŌČ -->
)
{\displaystyle \nu (\omega )}
–í –≤—č—Ä–į–∂–Ķ–Ĺ–ł–ł –≤—č—ą–Ķ —á–ł—Ā–Ľ–ĺ –≤—č–Ņ–į–≤—ą–ł—Ö –Ķ–ī–ł–Ĺ–ł—Ü –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł —ā–į–ļ:
ν őĹ -->
(
ω ŌČ -->
)
=
∑ ‚ąĎ -->
i
=
1
n
x
i
+
n
2
{\displaystyle \nu (\omega )={\frac {\sum \limits _{i=1}^{n}x_{i}+n}{2}}}
–í–≤–Ķ–ī—Ď–ľ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć –Ī–Ķ—Ä–Ĺ—É–Ľ–Ľ–ł–Ķ–≤—Ā–ļ–ł—Ö —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ:
i
=
1
;
n
¯ ¬Į -->
,
ξ őĺ -->
i
(
ω ŌČ -->
)
: : -->
P
(
{
ξ őĺ -->
i
=
1
}
)
=
p
,
P
(
{
ξ őĺ -->
i
=
− ‚ąí -->
1
}
)
=
q
,
p
+
q
=
1.
{\displaystyle i={\overline {1;n}},\quad \xi _{i}(\omega )\colon \quad \mathbb {P} {\bigl (}\{\xi _{i}=1\}{\bigr )}=p,\quad \mathbb {P} {\bigl (}\{\xi _{i}=-1\}{\bigr )}=q,\quad p+q=1.}
–Ē–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ
∑ ‚ąĎ -->
ω ŌČ -->
∈ ‚ąą -->
Ω ő© -->
P
(
{
ω ŌČ -->
}
)
=
1.
{\displaystyle \sum \limits _{\omega \in \Omega }\mathbb {P} {\bigl (}\{\omega \}{\bigr )}=1.}
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ
∑ ‚ąĎ -->
ω ŌČ -->
∈ ‚ąą -->
Ω ő© -->
P
(
{
ω ŌČ -->
}
)
=
∑ ‚ąĎ -->
ω ŌČ -->
∈ ‚ąą -->
Ω ő© -->
p
∑ ‚ąĎ -->
i
=
1
n
x
i
+
n
2
⋅ ‚čÖ -->
q
n
− ‚ąí -->
∑ ‚ąĎ -->
i
=
1
n
x
i
+
n
2
=
∑ ‚ąĎ -->
k
=
0
n
∑ ‚ąĎ -->
ω ŌČ -->
∈ ‚ąą -->
A
k
p
∑ ‚ąĎ -->
i
=
1
n
(
x
i
+
1
)
2
⋅ ‚čÖ -->
q
∑ ‚ąĎ -->
i
=
1
n
(
1
− ‚ąí -->
x
i
)
2
=
∑ ‚ąĎ -->
k
=
0
n
C
n
k
p
k
q
n
− ‚ąí -->
k
.
{\displaystyle \sum \limits _{\omega \in \Omega }\mathbb {P} {\bigl (}\{\omega \}{\bigr )}=\sum \limits _{\omega \in \Omega }p^{\frac {\sum \limits _{i=1}^{n}x_{i}+n}{2}}\cdot q^{n-{\frac {\sum \limits _{i=1}^{n}x_{i}+n}{2}}}=\sum \limits _{k=0}^{n}\sum \limits _{\omega \in A_{k}}p^{\frac {\sum \limits _{i=1}^{n}(x_{i}+1)}{2}}\cdot q^{\frac {\sum \limits _{i=1}^{n}(1-x_{i})}{2}}=\sum \limits _{k=0}^{n}C_{n}^{k}p^{k}q^{n-k}.}
x
i
+
1
2
∈ ‚ąą -->
{
0
;
1
}
.
{\displaystyle {\frac {x_{i}+1}{2}}\in \{0;1\}.}
∑ ‚ąĎ -->
k
=
0
n
C
n
k
p
k
q
n
− ‚ąí -->
k
=
(
p
+
q
)
n
=
1
{\displaystyle \sum \limits _{k=0}^{n}C_{n}^{k}p^{k}q^{n-k}=(p+q)^{n}=1}
p
+
q
=
1
{\displaystyle p+q=1}
◼ ‚óľ -->
{\displaystyle \blacksquare }
őĺi –Ē–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ
ξ őĺ -->
1
{\displaystyle \xi _{1}}
ξ őĺ -->
2
{\displaystyle \xi _{2}}
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ
–Ě–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā—Ć —Ā–Ľ—É—á–į–Ļ–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā, —á—ā–ĺ
P
(
{
ξ őĺ -->
1
=
1
}
∩ ‚ą© -->
{
ξ őĺ -->
2
=
1
}
)
=
P
(
{
ξ őĺ -->
1
=
1
}
)
P
(
{
ξ őĺ -->
2
=
1
}
)
,
{\displaystyle \mathbb {P} {\bigl (}\{\xi _{1}=1\}\cap \{\xi _{2}=1\}{\bigr )}=\mathbb {P} {\bigl (}\{\xi _{1}=1\}{\bigr )}\mathbb {P} {\bigl (}\{\xi _{2}=1\}{\bigr )},}
–Ņ–ĺ–ļ–į–∂–Ķ–ľ —ć—ā–ĺ:
P
(
{
ξ őĺ -->
1
=
1
}
∩ ‚ą© -->
{
ξ őĺ -->
2
=
1
}
)
=
P
(
{
ω ŌČ -->
: : -->
ω ŌČ -->
=
(
x
1
;
… ‚Ķ -->
;
x
n
)
,
x
1
=
1
,
x
2
=
1
}
)
=
{\displaystyle \mathbb {P} {\bigl (}\{\xi _{1}=1\}\cap \{\xi _{2}=1\}{\bigr )}=\mathbb {P} {\bigl (}\{\omega \colon \omega =(x_{1};\ldots ;x_{n}),\ x_{1}=1,\ x_{2}=1\}{\bigr )}=}
=
∑ ‚ąĎ -->
x
3
=
± ¬Ī -->
1
… ‚Ķ -->
x
n
=
± ¬Ī -->
1
p
2
+
∑ ‚ąĎ -->
i
=
3
n
x
i
+
n
2
⋅ ‚čÖ -->
q
n
− ‚ąí -->
2
+
∑ ‚ąĎ -->
i
=
3
n
x
i
+
n
2
=
p
2
∑ ‚ąĎ -->
x
3
=
± ¬Ī -->
1
… ‚Ķ -->
x
n
=
± ¬Ī -->
1
p
∑ ‚ąĎ -->
i
=
3
n
x
i
+
(
n
− ‚ąí -->
2
)
2
⋅ ‚čÖ -->
q
(
n
− ‚ąí -->
2
)
− ‚ąí -->
∑ ‚ąĎ -->
i
=
3
n
x
i
+
(
n
− ‚ąí -->
2
)
2
=
p
2
⋅ ‚čÖ -->
1.
{\displaystyle =\sum \limits _{\begin{smallmatrix}x_{3}=\pm 1\\\ldots {}\\x_{n}=\pm 1\end{smallmatrix}}p^{\frac {2+\sum \limits _{i=3}^{n}x_{i}+n}{2}}\cdot q^{n-{\frac {2+\sum \limits _{i=3}^{n}x_{i}+n}{2}}}=p^{2}\sum \limits _{\begin{smallmatrix}x_{3}=\pm 1\\\ldots {}\\x_{n}=\pm 1\end{smallmatrix}}p^{\frac {\sum \limits _{i=3}^{n}x_{i}+(n-2)}{2}}\cdot q^{(n-2)-{\frac {\sum \limits _{i=3}^{n}x_{i}+(n-2)}{2}}}=p^{2}\cdot 1.}
◼ ‚óľ -->
{\displaystyle \blacksquare }
–Ē–Ľ—Ź —Ā—Ö–Ķ–ľ—č –Ď–Ķ—Ä–Ĺ—É–Ľ–Ľ–ł –ī–ĺ–≥–ĺ–≤–ĺ—Ä–ł–ľ—Ā—Ź –ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ —Ā–ľ—č—Ā–Ľ–Ķ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č őĺ:
ξ őĺ -->
i
=
+
1
{\displaystyle \xi _{i}=+1}
ξ őĺ -->
i
=
− ‚ąí -->
1
{\displaystyle \xi _{i}=-1}
–í–≤–Ķ–ī—Ď–ľ –Ĺ–ĺ–≤–ĺ–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ:
S
0
=
0
{\displaystyle S_{0}=0}
S
k
=
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
,
1
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
{\displaystyle S_{k}=\xi _{1}+\ldots {}+\xi _{k},\quad 1\leqslant k\leqslant n}
–ß–ł—Ā–Ľ–ĺ
n
{\displaystyle n}
(
S
k
)
k
⩽ ‚©Ĺ -->
n
{\displaystyle (S_{k})_{k\leqslant n}}
S
k
+
1
=
S
k
+
ξ őĺ -->
k
+
1
{\displaystyle S_{k+1}=S_{k}+\xi _{k+1}}
S
k
{\displaystyle S_{k}}
A
{\displaystyle A}
B
{\displaystyle B}
A
⩽ ‚©Ĺ -->
0
{\displaystyle A\leqslant 0}
B
⩾ ‚©ĺ -->
0
{\displaystyle B\geqslant 0}
n
{\displaystyle n}
A
{\displaystyle A}
B
{\displaystyle B}
–Ē–į–Ľ–Ķ–Ķ, –Ņ—É—Ā—ā—Ć
x
{\displaystyle x}
x
∈ ‚ąą -->
Z
∩ ‚ą© -->
[
A
;
B
]
{\displaystyle x\in \mathbb {Z} \cap [A;B]}
0
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
{\displaystyle 0\leqslant k\leqslant n}
S
k
x
=
x
+
S
k
{\displaystyle S_{k}^{x}=x+S_{k}}
τ ŌĄ -->
k
x
=
min
{
l
: : -->
0
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
,
S
l
x
=
{
A
o
r
B
}
}
{\displaystyle \tau _{k}^{x}=\min {\bigl \{}l\colon 0\leqslant l\leqslant k,S_{l}^{x}=\{A\mathrm {~or~} B\}{\bigr \}}}
τ ŌĄ -->
k
x
=
k
{\displaystyle \tau _{k}^{x}=k}
A
<
S
l
x
<
B
∀ ‚ąÄ -->
l
: : -->
0
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
{\displaystyle A<S_{l}^{x}<B\quad \forall l\colon 0\leqslant l\leqslant k}
x
k
{\displaystyle x_{k}}
–Ē–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ
0
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
{\displaystyle 0\leqslant k\leqslant n}
x
∈ ‚ąą -->
[
A
;
B
]
∩ ‚ą© -->
Z
{\displaystyle x\in [A;B]\cap \mathbb {Z} }
τ ŌĄ -->
k
x
{\displaystyle \tau _{k}^{x}}
–ľ–ĺ–ľ–Ķ–Ĺ—ā–ĺ–ľ –ĺ—Ā—ā–į–Ĺ–ĺ–≤–ļ–ł , –ļ–ĺ—ā–ĺ—Ä—č–Ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ , –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č—Ö —Ā–ĺ–Ī—č—ā–ł–Ļ
Ω ő© -->
{\displaystyle \Omega }
∀ ‚ąÄ -->
l
<
k
{
ω ŌČ -->
: : -->
τ ŌĄ -->
k
x
=
l
}
{\displaystyle \forall l<k\quad \{\omega \colon \tau _{k}^{x}=l\}}
—Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ–Ķ –Ī–Ľ—É–∂–ī–į–Ĺ–ł–Ķ
{
S
i
x
: : -->
0
⩽ ‚©Ĺ -->
i
⩽ ‚©Ĺ -->
k
}
{\displaystyle \{S_{i}^{x}\colon 0\leqslant i\leqslant k\}}
x
{\displaystyle x}
[
A
;
B
]
{\displaystyle [A;B]}
l
{\displaystyle l}
A
k
x
=
∐ ‚ąź -->
0
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
{
ω ŌČ -->
: : -->
τ ŌĄ -->
k
x
=
l
,
S
l
x
=
A
}
{\displaystyle {\mathcal {A}}_{k}^{x}=\coprod \limits _{0\leqslant l\leqslant k}\{\omega \colon \tau _{k}^{x}=l,\ S_{l}^{x}=A\}}
B
k
x
=
∐ ‚ąź -->
0
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
{
ω ŌČ -->
: : -->
τ ŌĄ -->
k
x
=
l
,
S
l
x
=
B
}
{\displaystyle {\mathcal {B}}_{k}^{x}=\coprod \limits _{0\leqslant l\leqslant k}\{\omega \colon \tau _{k}^{x}=l,\ S_{l}^{x}=B\}}
0
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
{\displaystyle 0\leqslant k\leqslant n}
α őĪ -->
k
(
x
)
=
P
(
A
k
x
)
{\displaystyle \alpha _{k}(x)=\mathbb {P} ({\mathcal {A}}_{k}^{x})}
β ő≤ -->
k
(
x
)
=
P
(
B
k
x
)
{\displaystyle \beta _{k}(x)=\mathbb {P} ({\mathcal {B}}_{k}^{x})}
[
0
;
k
]
{\displaystyle [0;k]}
[
A
;
B
]
{\displaystyle [A;B]}
A
{\displaystyle A}
B
{\displaystyle B}
–ü—É—Ā—ā—Ć
A
<
x
<
B
{\displaystyle A<x<B}
α őĪ -->
0
(
x
)
=
β ő≤ -->
0
(
x
)
=
0
{\displaystyle \alpha _{0}(x)=\beta _{0}(x)=0}
0
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
{\displaystyle 0\leqslant k\leqslant n}
β ő≤ -->
k
(
x
)
=
P
(
B
k
x
)
=
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
+
1
)
⋅ ‚čÖ -->
P
(
{
ξ őĺ -->
1
=
1
}
)
+
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
− ‚ąí -->
1
)
⋅ ‚čÖ -->
P
(
{
ξ őĺ -->
1
=
− ‚ąí -->
1
}
)
.
{\displaystyle \beta _{k}(x)=\mathbb {P} ({\mathcal {B}}_{k}^{x})=\mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x+1)\cdot \mathbb {P} {\bigl (}\{\xi _{1}=1\}{\bigr )}+\mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x-1)\cdot \mathbb {P} {\bigl (}\{\xi _{1}=-1\}{\bigr )}.}
–Ē–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ
(1)
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
+
1
)
=
P
(
B
k
− ‚ąí -->
1
x
+
1
)
{\displaystyle \mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x+1)=\mathbb {P} ({\mathcal {B}}_{k-1}^{x+1})}
(2)
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
− ‚ąí -->
1
)
=
P
(
B
k
− ‚ąí -->
1
x
− ‚ąí -->
1
)
{\displaystyle \mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x-1)=\mathbb {P} ({\mathcal {B}}_{k-1}^{x-1})}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ.
(1) –Ē–ĺ–ļ–į–∂–Ķ–ľ, —á—ā–ĺ
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
+
1
)
=
P
(
B
k
− ‚ąí -->
1
x
+
1
)
{\displaystyle \mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x+1)=\mathbb {P} ({\mathcal {B}}_{k-1}^{x+1})}
B
k
x
=
{
ω ŌČ -->
: : -->
(
x
;
x
+
ξ őĺ -->
1
;
… ‚Ķ -->
;
x
+
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
)
∈ ‚ąą -->
B
k
x
}
{\displaystyle {\mathcal {B}}_{k}^{x}={\bigl \{}\omega \colon (x;x+\xi _{1};\ldots {};x+\xi _{1}+\ldots {}+\xi _{k})\in B_{k}^{x}{\bigr \}}}
B
k
x
{\displaystyle B_{k}^{x}}
(
x
;
x
+
x
1
;
… ‚Ķ -->
;
x
+
x
1
+
… ‚Ķ -->
+
x
k
)
,
x
i
=
± ¬Ī -->
1
{\displaystyle (x;x+x_{1};\ldots {};x+x_{1}+\ldots {}+x_{k}),\quad x_{i}=\pm 1}
[
0
;
k
]
{\displaystyle [0;k]}
(
A
;
B
)
{\displaystyle (A;B)}
B
{\displaystyle B}
B
{\displaystyle {\mathcal {B}}}
B
k
x
{\displaystyle B_{k}^{x}}
B
k
x
;
x
+
1
⊔ ‚äĒ -->
B
k
x
;
x
− ‚ąí -->
1
{\displaystyle B_{k}^{x;x+1}\sqcup B_{k}^{x;x-1}}
–Ē–ł–∑—ä—é–Ĺ–ļ—ā–Ĺ–ĺ–Ķ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–į–≤–ĺ–ľ–Ķ—Ä–Ĺ–ĺ –Ņ–ĺ –Ņ—Ä–ł—á–ł–Ĺ–Ķ —ā–ĺ–≥–ĺ, —á—ā–ĺ —É –Ľ—é–Ī–ĺ–Ļ —á–į—Ā—ā–ł—Ü—č, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ –Ņ–ĺ —ā—Ä–į–Ķ–ļ—ā–ĺ—Ä–ł–ł,
x
1
=
± ¬Ī -->
1
{\displaystyle x_{1}=\pm 1}
B
k
x
;
x
+
1
{\displaystyle B_{k}^{x;x+1}}
B
k
x
{\displaystyle B_{k}^{x}}
x
1
=
1
{\displaystyle x_{1}=1}
B
k
x
;
x
− ‚ąí -->
1
{\displaystyle B_{k}^{x;x-1}}
B
k
x
{\displaystyle B_{k}^{x}}
x
1
=
− ‚ąí -->
1
{\displaystyle x_{1}=-1}
(
x
;
x
+
1
;
x
+
1
+
x
2
;
… ‚Ķ -->
;
x
+
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
{\displaystyle (x;x+1;x+1+x_{2};\ldots {};x+1+x_{2}+\ldots +x_{k})}
B
k
x
;
x
+
1
{\displaystyle B_{k}^{x;x+1}}
(
x
+
1
;
x
+
1
+
x
2
;
… ‚Ķ -->
;
x
+
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
{\displaystyle (x+1;x+1+x_{2};\ldots {};x+1+x_{2}+\ldots +x_{k})}
B
k
− ‚ąí -->
1
x
+
1
{\displaystyle B_{k-1}^{x+1}}
–í–∑–į–ł–ľ–Ĺ–ĺ-–ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ī–ĺ–ļ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ĺ—ā –Ņ—Ä–ĺ—ā–ł–≤–Ĺ–ĺ–≥–ĺ . –ü—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ, —á—ā–ĺ
x
1
=
− ‚ąí -->
1
{\displaystyle x_{1}=-1}
(
x
;
x
− ‚ąí -->
1
;
x
− ‚ąí -->
1
+
x
2
;
… ‚Ķ -->
;
x
− ‚ąí -->
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
{\displaystyle (x;x-1;x-1+x_{2};\ldots ;x-1+x_{2}+\ldots +x_{k})}
k
{\displaystyle k}
k
+
2
{\displaystyle k+2}
S
k
+
1
=
S
k
+
ξ őĺ -->
k
+
1
{\displaystyle S_{k+1}=S_{k}+\xi _{k+1}}
P
(
{
(
x
+
1
;
x
+
1
+
x
2
;
… ‚Ķ -->
;
x
+
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
∈ ‚ąą -->
B
k
− ‚ąí -->
1
x
+
1
}
)
=
P
(
{
(
x
+
1
;
x
+
1
+
x
1
;
… ‚Ķ -->
;
x
+
1
+
x
1
+
… ‚Ķ -->
+
x
k
− ‚ąí -->
1
)
∈ ‚ąą -->
B
k
− ‚ąí -->
1
x
+
1
}
)
=
d
e
f
P
(
B
k
− ‚ąí -->
1
x
+
1
)
{\displaystyle \mathbb {P} {\Bigl (}{\big \{}(x+1;x+1+x_{2};\ldots ;x+1+x_{2}+\ldots +x_{k})\in B_{k-1}^{x+1}{\bigr \}}{\Bigr )}=\mathbb {P} {\Bigl (}{\bigl \{}(x+1;x+1+x_{1};\ldots ;x+1+x_{1}+\ldots +x_{k-1})\in B_{k-1}^{x+1}{\bigr \}}{\Bigr )}{\mathrel {\stackrel {\rm {def}}{=}}}\mathbb {P} ({\mathcal {B}}_{k-1}^{x+1})}
ξ őĺ -->
i
{\displaystyle \xi _{i}}
–Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č–Ķ –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–Ķ —Ā–Ľ—É—á–į–Ļ–Ĺ—č–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č ).
–°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ł –ī—Ä—É–≥–ĺ–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į:
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
+
1
)
=
P
(
B
k
x
∣ ‚ą£ -->
ξ őĺ -->
1
=
1
)
=
P
(
(
x
;
x
+
ξ őĺ -->
1
;
… ‚Ķ -->
;
x
+
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
)
∈ ‚ąą -->
B
k
x
∣ ‚ą£ -->
ξ őĺ -->
1
=
1
)
=
{\displaystyle \mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x+1)=\mathbb {P} ({\mathcal {B}}_{k}^{x}\mid \xi _{1}=1)=\mathbb {P} {\bigl (}(x;x+\xi _{1};\ldots {};x+\xi _{1}+\ldots {}+\xi _{k})\in B_{k}^{x}\mid \xi _{1}=1{\bigr )}=}
=
P
(
(
x
;
x
+
ξ őĺ -->
1
;
… ‚Ķ -->
;
x
+
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
)
∈ ‚ąą -->
B
k
x
∩ ‚ą© -->
ξ őĺ -->
1
=
1
)
P
(
{
ξ őĺ -->
1
=
1
}
)
=
P
(
(
x
;
x
+
1
;
… ‚Ķ -->
;
x
+
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
)
∈ ‚ąą -->
B
k
x
∩ ‚ą© -->
ξ őĺ -->
1
=
1
)
P
(
{
ξ őĺ -->
1
=
1
}
)
=
{\displaystyle ={\frac {\mathbb {P} {\bigl (}(x;x+\xi _{1};\ldots {};x+\xi _{1}+\ldots {}+\xi _{k})\in B_{k}^{x}\cap \xi _{1}=1{\bigr )}}{\mathbb {P} (\{\xi _{1}=1\})}}={\frac {\mathbb {P} {\bigl (}(x;x+1;\ldots {};x+1+\ldots {}+\xi _{k})\in B_{k}^{x}\cap \xi _{1}=1{\bigr )}}{\mathbb {P} (\{\xi _{1}=1\})}}=}
=
P
(
{
(
x
;
x
+
1
;
x
+
1
+
ξ őĺ -->
2
;
… ‚Ķ -->
;
x
+
1
+
ξ őĺ -->
2
+
… ‚Ķ -->
+
ξ őĺ -->
k
)
∈ ‚ąą -->
B
k
x
}
)
=
P
(
{
(
x
;
x
+
1
;
x
+
1
+
ξ őĺ -->
1
;
… ‚Ķ -->
;
x
+
1
+
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
− ‚ąí -->
1
)
∈ ‚ąą -->
B
k
x
}
)
=
{\displaystyle =\mathbb {P} {\bigl (}\{(x;x+1;x+1+\xi _{2};\ldots {};x+1+\xi _{2}+\ldots {}+\xi _{k})\in B_{k}^{x}\}{\bigr )}=\mathbb {P} {\bigl (}\{(x;x+1;x+1+\xi _{1};\ldots {};x+1+\xi _{1}+\ldots {}+\xi _{k-1})\in B_{k}^{x}\}{\bigr )}=}
=
P
(
{
(
x
;
x
+
1
;
x
+
1
+
ξ őĺ -->
1
;
… ‚Ķ -->
;
x
+
1
+
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
k
− ‚ąí -->
1
)
∈ ‚ąą -->
B
k
− ‚ąí -->
1
x
+
1
}
)
=
P
(
B
k
− ‚ąí -->
1
x
+
1
)
=
β ő≤ -->
k
− ‚ąí -->
1
(
x
+
1
)
{\displaystyle =\mathbb {P} {\bigl (}\{(x;x+1;x+1+\xi _{1};\ldots {};x+1+\xi _{1}+\ldots {}+\xi _{k-1})\in B_{k-1}^{x+1}\}{\bigr )}=\mathbb {P} ({\mathcal {B}}_{k-1}^{x+1})=\beta _{k-1}(x+1)}
–≠—ā–ĺ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ –Ņ–ĺ—ā–ĺ–ľ—É, —á—ā–ĺ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č (—ć—ā–ĺ –Ī—č–Ľ–ĺ –ī–ĺ–ļ–į–∑–į–Ĺ–ĺ —Ä–į–Ĺ–Ķ–Ķ).
(2) –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ –ī–ĺ–ļ–į–∂–Ķ–ľ, —á—ā–ĺ
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
− ‚ąí -->
1
)
=
P
(
B
k
− ‚ąí -->
1
x
+
1
)
{\displaystyle \mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x-1)=\mathbb {P} ({\mathcal {B}}_{k-1}^{x+1})}
–ö–į–∂–ī–į—Ź —ā—Ä–į–Ķ–ļ—ā–ĺ—Ä–ł—Ź
(
x
;
x
− ‚ąí -->
1
;
x
− ‚ąí -->
1
+
x
2
;
… ‚Ķ -->
;
x
− ‚ąí -->
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
{\displaystyle (x;x-1;x-1+x_{2};\ldots {};x-1+x_{2}+\ldots +x_{k})}
B
k
x
;
x
+
1
{\displaystyle B_{k}^{x;x+1}}
(
x
− ‚ąí -->
1
;
x
− ‚ąí -->
1
+
x
2
;
… ‚Ķ -->
;
x
− ‚ąí -->
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
{\displaystyle (x-1;x-1+x_{2};\ldots {};x-1+x_{2}+\ldots +x_{k})}
B
k
− ‚ąí -->
1
x
− ‚ąí -->
1
{\displaystyle B_{k-1}^{x-1}}
P
(
{
(
x
− ‚ąí -->
1
;
x
− ‚ąí -->
1
+
x
2
;
… ‚Ķ -->
;
x
− ‚ąí -->
1
+
x
2
+
… ‚Ķ -->
+
x
k
)
∈ ‚ąą -->
B
k
− ‚ąí -->
1
x
− ‚ąí -->
1
}
)
=
P
(
{
(
x
− ‚ąí -->
1
;
x
− ‚ąí -->
1
+
x
1
;
… ‚Ķ -->
;
x
− ‚ąí -->
1
+
x
1
+
… ‚Ķ -->
+
x
k
− ‚ąí -->
1
)
∈ ‚ąą -->
B
k
− ‚ąí -->
1
x
− ‚ąí -->
1
}
)
=
d
e
f
P
(
B
k
− ‚ąí -->
1
x
− ‚ąí -->
1
)
.
{\displaystyle \mathbb {P} {\Bigl (}{\bigl \{}(x-1;x-1+x_{2};\ldots ;x-1+x_{2}+\ldots +x_{k})\in B_{k-1}^{x-1}{\bigr \}}{\Bigr )}=\mathbb {P} {\Bigl (}{\bigl \{}(x-1;x-1+x_{1};\ldots ;x-1+x_{1}+\ldots +x_{k-1})\in B_{k-1}^{x-1}{\bigr \}}{\Bigr )}{\mathrel {\stackrel {\rm {def}}{=}}}\mathbb {P} ({\mathcal {B}}_{k-1}^{x-1}).}
◼ ‚óľ -->
{\displaystyle \blacksquare }
–ė–∑ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź
β ő≤ -->
k
(
x
)
{\displaystyle \beta _{k}(x)}
x
∈ ‚ąą -->
(
A
;
B
)
{\displaystyle x\in (A;B)}
k
⩽ ‚©Ĺ -->
n
{\displaystyle k\leqslant n}
P
(
B
k
x
)
=
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
+
1
)
⋅ ‚čÖ -->
p
+
P
(
B
k
x
∣ ‚ą£ -->
S
1
x
=
x
− ‚ąí -->
1
)
⋅ ‚čÖ -->
q
=
P
(
B
k
− ‚ąí -->
1
x
+
1
)
⋅ ‚čÖ -->
p
+
P
(
B
k
− ‚ąí -->
1
x
− ‚ąí -->
1
)
⋅ ‚čÖ -->
q
=
p
β ő≤ -->
k
− ‚ąí -->
1
(
x
+
1
)
+
q
β ő≤ -->
k
− ‚ąí -->
1
(
x
− ‚ąí -->
1
)
.
{\displaystyle \mathbb {P} ({\mathcal {B}}_{k}^{x})=\mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x+1)\cdot p+\mathbb {P} ({\mathcal {B}}_{k}^{x}\mid S_{1}^{x}=x-1)\cdot q=\mathbb {P} ({\mathcal {B}}_{k-1}^{x+1})\cdot p+\mathbb {P} ({\mathcal {B}}_{k-1}^{x-1})\cdot q=p\beta _{k-1}(x+1)+q\beta _{k-1}(x-1).}
β ő≤ -->
l
(
B
)
=
1
{\displaystyle \beta _{l}(B)=1}
β ő≤ -->
l
(
A
)
=
0
{\displaystyle \beta _{l}(A)=0}
l
∈ ‚ąą -->
[
0
;
n
]
{\displaystyle l\in [0;n]}
–§–ĺ—Ä–ľ—É–Ľ–į –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł —ā–į–ļ–∂–Ķ –ī–į—Ď—ā –Ĺ–į–ľ —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā:
α őĪ -->
k
(
x
)
=
p
α őĪ -->
k
− ‚ąí -->
1
(
x
+
1
)
+
q
α őĪ -->
k
− ‚ąí -->
1
(
x
− ‚ąí -->
1
)
{\displaystyle \alpha _{k}(x)=p\alpha _{k-1}(x+1)+q\alpha _{k-1}(x-1)}
B
k
− ‚ąí -->
1
⊂ ‚äā -->
B
k
{\displaystyle {\mathcal {B}}_{k-1}\subset {\mathcal {B}}_{k}}
β ő≤ -->
k
− ‚ąí -->
1
(
x
)
⩽ ‚©Ĺ -->
β ő≤ -->
k
(
x
)
⩽ ‚©Ĺ -->
1
{\displaystyle \beta _{k-1}(x)\leqslant \beta _{k}(x)\leqslant 1}
k
⩽ ‚©Ĺ -->
n
{\displaystyle k\leqslant n}
x
j
− ‚ąí -->
1
=
± ¬Ī -->
1
{\displaystyle x_{j-1}=\pm 1}
(
j
;
S
j
x
)
{\displaystyle (j;S_{j}^{x})}
(
j
− ‚ąí -->
1
;
S
j
x
− ‚ąí -->
1
)
{\displaystyle (j-1;S_{j}^{x}-1)}
ξ őĺ -->
j
=
1
{\displaystyle \xi _{j}=1}
(
j
− ‚ąí -->
1
;
S
j
x
+
1
)
{\displaystyle (j-1;S_{j}^{x}+1)}
j
⩽ ‚©Ĺ -->
k
{\displaystyle j\leqslant k}
–ü—Ä–ł –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ł—Ö
n
{\displaystyle n}
β ő≤ -->
n
(
x
)
{\displaystyle \beta _{n}(x)}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
β ő≤ -->
(
x
)
=
p
β ő≤ -->
(
x
+
1
)
+
q
β ő≤ -->
(
x
− ‚ąí -->
1
)
{\displaystyle \beta (x)=p\beta (x+1)+q\beta (x-1)}
β ő≤ -->
(
B
)
=
1
{\displaystyle \beta (B)=1}
B
{\displaystyle B}
β ő≤ -->
(
A
)
=
0
{\displaystyle \beta (A)=0}
A
{\displaystyle A}
lim
l
→ ‚Üí -->
∞ ‚ąě -->
β ő≤ -->
l
(
B
)
=
β ő≤ -->
(
B
)
{\displaystyle \lim \limits _{l\rightarrow \infty }\beta _{l}(B)=\beta (B)}
–°–Ĺ–į—á–į–Ľ–į –Ņ–ĺ–Ľ—É—á–ł–ľ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
β ő≤ -->
(
x
)
=
p
β ő≤ -->
(
x
+
1
)
+
q
β ő≤ -->
(
x
− ‚ąí -->
1
)
{\displaystyle \beta (x)=p\beta (x+1)+q\beta (x-1)}
p
≠ ‚Ȇ -->
q
{\displaystyle p\neq q}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
β ő≤ -->
(
x
)
=
c
o
n
s
t
=
a
{\displaystyle \beta (x)=\mathrm {const} =a}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
q
p
{\displaystyle {\frac {q}{p}}}
p
+
q
=
1
{\displaystyle p+q=1}
(
q
p
)
x
=
q
x
(
p
+
q
)
p
x
=
q
x
p
x
− ‚ąí -->
1
+
q
x
+
1
p
x
=
p
q
x
+
1
p
x
+
1
+
q
q
x
− ‚ąí -->
1
p
x
− ‚ąí -->
1
=
p
(
q
p
)
x
+
1
+
q
(
q
p
)
x
− ‚ąí -->
1
{\displaystyle \left({\frac {q}{p}}\right)^{x}={\frac {q^{x}(p+q)}{p^{x}}}={\frac {q^{x}}{p^{x-1}}}+{\frac {q^{x+1}}{p^{x}}}=p{\frac {q^{x+1}}{p^{x+1}}}+q{\frac {q^{x-1}}{p^{x-1}}}=p\left({\frac {q}{p}}\right)^{x+1}+q\left({\frac {q}{p}}\right)^{x-1}}
β ő≤ -->
(
x
)
=
b
⋅ ‚čÖ -->
(
q
p
)
x
{\displaystyle \beta (x)=b\cdot \left({\frac {q}{p}}\right)^{x}}
p
+
q
=
1
{\displaystyle p+q=1}
–Ę–Ķ–Ņ–Ķ—Ä—Ć —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ĺ–Ī—Č–Ķ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ:
β ő≤ -->
(
x
)
=
a
+
b
(
q
p
)
x
{\displaystyle \beta (x)=a+b\left({\frac {q}{p}}\right)^{x}}
β ő≤ -->
(
A
)
=
a
+
b
(
q
p
)
A
=
0
{\displaystyle \beta (A)=a+b\left({\frac {q}{p}}\right)^{A}=0}
β ő≤ -->
(
B
)
=
a
+
b
(
q
p
)
B
=
1
{\displaystyle \beta (B)=a+b\left({\frac {q}{p}}\right)^{B}=1}
β ő≤ -->
(
x
)
=
β ő≤ -->
(
x
)
− ‚ąí -->
0
1
− ‚ąí -->
0
=
β ő≤ -->
(
x
)
− ‚ąí -->
β ő≤ -->
(
A
)
β ő≤ -->
(
B
)
− ‚ąí -->
β ő≤ -->
(
A
)
=
a
+
b
(
q
p
)
x
− ‚ąí -->
(
a
+
b
(
q
p
)
A
)
a
+
b
(
q
p
)
B
− ‚ąí -->
(
a
+
b
(
q
p
)
A
)
=
(
q
p
)
x
− ‚ąí -->
(
q
p
)
A
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
.
{\displaystyle \beta (x)={\frac {\beta (x)-0}{1-0}}={\frac {\beta (x)-\beta (A)}{\beta (B)-\beta (A)}}={\frac {a+b\left({\frac {q}{p}}\right)^{x}-\left(a+b\left({\frac {q}{p}}\right)^{A}\right)}{a+b\left({\frac {q}{p}}\right)^{B}-\left(a+b\left({\frac {q}{p}}\right)^{A}\right)}}={\frac {\left({\frac {q}{p}}\right)^{x}-\left({\frac {q}{p}}\right)^{A}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}.}
–Ē–ĺ–ļ–į–∂–Ķ–ľ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ī–į–Ĺ–Ĺ–ĺ–Ļ –∑–į–ī–į—á–ł. –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ –Ņ–ĺ–ļ–į–∂–Ķ–ľ, —á—ā–ĺ –Ľ—é–Ī–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –∑–į–ī–į—á–ł
β ő≤ -->
(
x
)
=
p
β ő≤ -->
(
x
+
1
)
+
q
β ő≤ -->
(
x
− ‚ąí -->
1
)
{\displaystyle \beta (x)=p\beta (x+1)+q\beta (x-1)}
(
q
p
)
x
− ‚ąí -->
(
q
p
)
A
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
{\displaystyle {\frac {\left({\frac {q}{p}}\right)^{x}-\left({\frac {q}{p}}\right)^{A}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}}
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ
β ő≤ -->
ˇ ňá -->
(
x
)
{\displaystyle {\check {\beta }}(x)}
β ő≤ -->
ˇ ňá -->
(
A
)
=
0
{\displaystyle {\check {\beta }}(A)=0}
β ő≤ -->
ˇ ňá -->
(
B
)
=
1
{\displaystyle {\check {\beta }}(B)=1}
a
ˇ ňá -->
{\displaystyle {\check {a}}}
b
ˇ ňá -->
{\displaystyle {\check {b}}}
a
ˇ ňá -->
+
b
ˇ ňá -->
(
q
p
)
A
=
β ő≤ -->
ˇ ňá -->
(
A
)
{\displaystyle {\check {a}}+{\check {b}}\left({\frac {q}{p}}\right)^{A}={\check {\beta }}(A)}
a
ˇ ňá -->
+
b
ˇ ňá -->
(
q
p
)
A
+
1
=
β ő≤ -->
ˇ ňá -->
(
A
+
1
)
{\displaystyle {\check {a}}+{\check {b}}\left({\frac {q}{p}}\right)^{A+1}={\check {\beta }}(A+1)}
β ő≤ -->
ˇ ňá -->
(
A
+
2
)
=
a
ˇ ňá -->
+
b
ˇ ňá -->
(
q
p
)
A
+
2
{\displaystyle {\check {\beta }}(A+2)={\check {a}}+{\check {b}}\left({\frac {q}{p}}\right)^{A+2}}
β ő≤ -->
ˇ ňá -->
(
x
)
=
a
ˇ ňá -->
+
b
ˇ ňá -->
(
q
p
)
x
{\displaystyle {\check {\beta }}(x)={\check {a}}+{\check {b}}\left({\frac {q}{p}}\right)^{x}}
(
q
p
)
x
− ‚ąí -->
(
q
p
)
A
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
{\displaystyle {\frac {\left({\frac {q}{p}}\right)^{x}-\left({\frac {q}{p}}\right)^{A}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}}
α őĪ -->
(
x
)
{\displaystyle \alpha (x)}
◼ ‚óľ -->
{\displaystyle \blacksquare }
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –≤–ĺ–Ņ—Ä–ĺ—Ā –ĺ –Ī—č—Ā—ā—Ä–ĺ—ā–Ķ –Ņ—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł
α őĪ -->
n
(
x
)
{\displaystyle \alpha _{n}(x)}
β ő≤ -->
n
(
x
)
{\displaystyle \beta _{n}(x)}
α őĪ -->
(
x
)
{\displaystyle \alpha (x)}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
x
=
0
{\displaystyle x=0}
α őĪ -->
n
(
0
)
=
α őĪ -->
n
{\displaystyle \alpha _{n}(0)=\alpha _{n}}
β ő≤ -->
n
(
0
)
=
β ő≤ -->
n
{\displaystyle \beta _{n}(0)=\beta _{n}}
γ ő≥ -->
n
=
1
− ‚ąí -->
α őĪ -->
n
− ‚ąí -->
β ő≤ -->
n
{\displaystyle \gamma _{n}=1-\alpha _{n}-\beta _{n}}
γ ő≥ -->
n
{\displaystyle \gamma _{n}}
γ ő≥ -->
n
=
P
{
ω ŌČ -->
: : -->
A
<
S
k
<
B
;
0
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
}
{\displaystyle \gamma _{n}=\mathbb {P} \{\omega \colon A<S_{k}<B;0\leqslant k\leqslant n\}}
ω ŌČ -->
{\displaystyle \omega }
⋂ ‚čā -->
0
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
n
{
A
<
S
k
<
B
}
{\displaystyle \bigcap \limits _{0\leqslant k\leqslant n}\{A<S_{k}<B\}}
n
=
r
m
{\displaystyle n=rm}
r
,
m
∈ ‚ąą -->
Z
{\displaystyle r,m\in \mathbb {Z} }
ζ ő∂ -->
n
: : -->
ζ ő∂ -->
1
=
∑ ‚ąĎ -->
i
=
1
m
ξ őĺ -->
i
,
ζ ő∂ -->
2
=
∑ ‚ąĎ -->
i
=
m
+
1
2
m
ξ őĺ -->
i
,
… ‚Ķ -->
,
ζ ő∂ -->
r
=
∑ ‚ąĎ -->
i
=
m
(
r
− ‚ąí -->
1
)
r
m
ξ őĺ -->
i
{\displaystyle \zeta _{n}\colon \zeta _{1}=\sum \limits _{i=1}^{m}\xi _{i},~\zeta _{2}=\sum \limits _{i=m+1}^{2m}\xi _{i},~\ldots {},~\zeta _{r}=\sum \limits _{i=m(r-1)}^{rm}\xi _{i}}
C
=
|
A
|
+
B
{\displaystyle C=|A|+B}
{
A
<
S
k
<
B
;
1
⩽ ‚©Ĺ -->
k
⩽ ‚©Ĺ -->
r
m
}
⊆ ‚äÜ -->
{
|
ζ ő∂ -->
1
|
<
C
;
… ‚Ķ -->
;
|
ζ ő∂ -->
r
|
<
C
}
{\displaystyle \{A<S_{k}<B;1\leqslant k\leqslant rm\}\subseteq {\bigl \{}|\zeta _{1}|<C;\ldots {};|\zeta _{r}|<C{\bigr \}}}
m
{\displaystyle m}
x
i
{\displaystyle x_{i}}
ő∂i –Ē–ĺ–ļ–į–∂–Ķ–ľ, —á—ā–ĺ
ζ ő∂ -->
j
{\displaystyle \zeta _{j}}
–Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č –ł –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–Ķ . –Ē–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –ī–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ –ĺ–Ĺ–ł –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č, —ā–į–ļ –ļ–į–ļ –≤—Ā–Ķ –ĺ–Ĺ–ł –ł–ľ–Ķ—é—ā –Ī–ł–Ĺ–ĺ–ľ–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ .
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ
–Ē–ĺ–ļ–į–∂–Ķ–ľ, —á—ā–ĺ
P
(
{
ζ ő∂ -->
1
=
m
}
∩ ‚ą© -->
{
ζ ő∂ -->
2
=
m
}
)
=
P
(
{
ζ ő∂ -->
1
=
m
}
)
⋅ ‚čÖ -->
P
(
{
ζ ő∂ -->
2
=
m
}
)
.
{\displaystyle \mathbb {P} {\bigl (}\{\zeta _{1}=m\}\cap \{\zeta _{2}=m\}{\bigr )}=\mathbb {P} {\bigl (}\{\zeta _{1}=m\}{\bigr )}\cdot \mathbb {P} {\bigl (}\{\zeta _{2}=m\}{\bigr )}.}
P
(
{
ζ ő∂ -->
1
=
m
}
∩ ‚ą© -->
{
ζ ő∂ -->
2
=
m
}
)
=
P
(
{
∑ ‚ąĎ -->
i
=
1
m
ξ őĺ -->
i
=
m
}
∩ ‚ą© -->
{
∑ ‚ąĎ -->
i
=
m
+
1
2
m
ξ őĺ -->
i
=
m
}
)
=
{\displaystyle \mathbb {P} {\bigl (}\{\zeta _{1}=m\}\cap \{\zeta _{2}=m\}{\bigr )}=\mathbb {P} \left(\left\{\sum \limits _{i=1}^{m}\xi _{i}=m\right\}\cap \left\{\sum \limits _{i=m+1}^{2m}\xi _{i}=m\right\}\right)=}
=
P
(
{
ξ őĺ -->
1
;
… ‚Ķ -->
;
m
=
1
}
∩ ‚ą© -->
{
ξ őĺ -->
m
+
1
;
… ‚Ķ -->
;
2
m
=
1
}
)
=
P
2
m
(
{
ξ őĺ -->
i
=
1
}
)
=
P
(
{
ζ ő∂ -->
1
=
m
}
)
⋅ ‚čÖ -->
P
(
{
ζ ő∂ -->
2
=
m
}
)
{\displaystyle =\mathbb {P} {\bigl (}\{\xi _{1;\ldots ;m}=1\}\cap \{\xi _{m+1;\ldots ;2m}=1\}{\bigr )}=\mathbb {P} ^{2m}{\bigl (}\{\xi _{i}=1\}{\bigr )}=\mathbb {P} {\bigl (}\{\zeta _{1}=m\}{\bigr )}\cdot \mathbb {P} {\bigl (}\{\zeta _{2}=m\}{\bigr )}}
◼ ‚óľ -->
{\displaystyle \blacksquare }
–ė–∑ —ā–ĺ–Ľ—Ć–ļ–ĺ —á—ā–ĺ –ī–ĺ–ļ–į–∑–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–Ľ–Ķ–ī—É–Ķ—ā —á—ā–ĺ
γ ő≥ -->
n
⩽ ‚©Ĺ -->
P
(
{
|
ζ ő∂ -->
1
|
;
… ‚Ķ -->
;
|
ζ ő∂ -->
r
|
<
C
}
)
=
∏ ‚ąŹ -->
i
=
1
r
P
(
{
|
ζ ő∂ -->
i
|
<
C
}
)
=
(
P
(
{
|
ζ ő∂ -->
1
|
<
C
}
)
)
r
{\displaystyle \gamma _{n}\leqslant \mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{1}|;\ldots ;|\zeta _{r}|<C{\bigr \}}{\Bigr )}=\prod \limits _{i=1}^{r}\mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{i}|<C{\bigr \}}{\Bigr )}={\biggl (}\mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{1}|<C{\bigr \}}{\Bigr )}{\biggr )}^{r}}
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł—é :
V
a
r
(
ζ ő∂ -->
1
)
=
m
(
1
− ‚ąí -->
(
p
− ‚ąí -->
q
)
2
)
{\displaystyle \mathrm {Var} (\zeta _{1})=m{\bigl (}1-(p-q)^{2}{\bigr )}}
1
− ‚ąí -->
(
p
− ‚ąí -->
q
)
2
=
1
− ‚ąí -->
(
(
p
+
q
)
2
− ‚ąí -->
4
p
q
)
{\displaystyle 1-(p-q)^{2}=1-{\bigl (}(p+q)^{2}-4pq{\bigr )}}
ξ őĺ -->
{\displaystyle \xi }
–Ī–Ķ—Ä–Ĺ—É–Ľ–Ľ–ł–Ķ–≤—Ā–ļ–į—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į ), –Ņ–ĺ—ć—ā–ĺ–ľ—É –ī–Ľ—Ź –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ł—Ö
m
{\displaystyle m}
0
<
p
<
1
{\displaystyle 0<p<1}
P
(
{
|
ζ ő∂ -->
1
|
<
C
}
)
⩽ ‚©Ĺ -->
ε őĶ -->
1
{\displaystyle \mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{1}|<C{\bigr \}}{\Bigr )}\leqslant \varepsilon _{1}}
ε őĶ -->
1
<
1
{\displaystyle \varepsilon _{1}<1}
P
(
{
|
ζ ő∂ -->
1
|
⩽ ‚©Ĺ -->
C
}
)
=
1
{\displaystyle \mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{1}|\leqslant C{\bigr \}}{\Bigr )}=1}
V
a
r
(
ζ ő∂ -->
1
)
⩽ ‚©Ĺ -->
C
2
{\displaystyle \mathrm {Var} (\zeta _{1})\leqslant C^{2}}
p
=
0
{\displaystyle p=0}
p
=
1
{\displaystyle p=1}
m
{\displaystyle m}
P
(
{
|
ζ ő∂ -->
1
|
<
C
}
)
=
0
{\displaystyle \mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{1}|<C{\bigr \}}{\Bigr )}=0}
P
(
{
|
ζ ő∂ -->
1
|
<
C
}
)
⩽ ‚©Ĺ -->
ε őĶ -->
1
{\displaystyle \mathbb {P} {\Bigl (}{\bigl \{}|\zeta _{1}|<C{\bigr \}}{\Bigr )}\leqslant \varepsilon _{1}}
∀ ‚ąÄ -->
p
∈ ‚ąą -->
[
0
;
1
]
{\displaystyle \forall p\in [0;1]}
γ ő≥ -->
n
⩽ ‚©Ĺ -->
ε őĶ -->
n
{\displaystyle \gamma _{n}\leqslant \varepsilon ^{n}}
ε őĶ -->
=
ε őĶ -->
1
1
m
<
1
{\displaystyle \varepsilon =\varepsilon _{1}^{\frac {1}{m}}<1}
α őĪ -->
+
β ő≤ -->
=
1
{\displaystyle \alpha +\beta =1}
(
α őĪ -->
− ‚ąí -->
α őĪ -->
n
)
− ‚ąí -->
(
β ő≤ -->
− ‚ąí -->
β ő≤ -->
n
)
=
γ ő≥ -->
n
{\displaystyle (\alpha -\alpha _{n})-(\beta -\beta _{n})=\gamma _{n}}
α őĪ -->
⩾ ‚©ĺ -->
α őĪ -->
n
{\displaystyle \alpha \geqslant \alpha _{n}}
β ő≤ -->
⩾ ‚©ĺ -->
β ő≤ -->
n
{\displaystyle \beta \geqslant \beta _{n}}
0
⩽ ‚©Ĺ -->
α őĪ -->
− ‚ąí -->
α őĪ -->
n
⩽ ‚©Ĺ -->
γ ő≥ -->
n
⩽ ‚©Ĺ -->
ε őĶ -->
n
{\displaystyle 0\leqslant \alpha -\alpha _{n}\leqslant \gamma _{n}\leqslant \varepsilon ^{n}}
0
⩽ ‚©Ĺ -->
β ő≤ -->
− ‚ąí -->
β ő≤ -->
n
⩽ ‚©Ĺ -->
γ ő≥ -->
n
⩽ ‚©Ĺ -->
ε őĶ -->
n
{\displaystyle 0\leqslant \beta -\beta _{n}\leqslant \gamma _{n}\leqslant \varepsilon ^{n}}
ε őĶ -->
<
1
{\displaystyle \varepsilon <1}
α őĪ -->
(
x
)
− ‚ąí -->
α őĪ -->
n
(
x
)
{\displaystyle \alpha (x)-\alpha _{n}(x)}
β ő≤ -->
(
x
)
− ‚ąí -->
β ő≤ -->
n
(
x
)
{\displaystyle \beta (x)-\beta _{n}(x)}
α őĪ -->
− ‚ąí -->
α őĪ -->
n
{\displaystyle \alpha -\alpha _{n}}
β ő≤ -->
− ‚ąí -->
β ő≤ -->
n
{\displaystyle \beta -\beta _{n}}
A
1
=
A
− ‚ąí -->
x
{\displaystyle A_{1}=A-x}
B
1
=
B
− ‚ąí -->
x
{\displaystyle B_{1}=B-x}
–í–Ķ—Ä–Ĺ—Ď–ľ—Ā—Ź –ļ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł—é
α őĪ -->
(
x
)
{\displaystyle \alpha (x)}
(
q
p
)
x
− ‚ąí -->
(
q
p
)
A
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
{\displaystyle {\frac {\left({\frac {q}{p}}\right)^{x}-\left({\frac {q}{p}}\right)^{A}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}}
β ő≤ -->
(
x
)
=
p
β ő≤ -->
(
x
+
1
)
+
q
β ő≤ -->
(
x
− ‚ąí -->
1
)
{\displaystyle \beta (x)=p\beta (x+1)+q\beta (x-1)}
α őĪ -->
(
x
)
=
p
α őĪ -->
(
x
+
1
)
+
q
α őĪ -->
(
x
− ‚ąí -->
1
)
{\displaystyle \alpha (x)=p\alpha (x+1)+q\alpha (x-1)}
α őĪ -->
(
A
)
=
1
{\displaystyle \alpha (A)=1}
α őĪ -->
(
B
)
=
0
{\displaystyle \alpha (B)=0}
α őĪ -->
(
x
)
=
(
q
p
)
B
− ‚ąí -->
(
q
p
)
x
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
,
A
⩽ ‚©Ĺ -->
x
⩽ ‚©Ĺ -->
B
.
{\displaystyle \alpha (x)={\frac {\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{x}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}},\qquad A\leqslant x\leqslant B.}
–Ě–Ķ—ā—Ä—É–ī–Ĺ–ĺ –∑–į–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ
α őĪ -->
(
x
)
+
β ő≤ -->
(
x
)
=
(
q
p
)
B
− ‚ąí -->
(
q
p
)
x
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
+
(
q
p
)
x
− ‚ąí -->
(
q
p
)
A
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
=
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
=
1
{\displaystyle \alpha (x)+\beta (x)={\frac {\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{x}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}+{\frac {\left({\frac {q}{p}}\right)^{x}-\left({\frac {q}{p}}\right)^{A}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}={\frac {\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}=1}
p
∈ ‚ąą -->
[
0
;
1
]
{\displaystyle p\in [0;1]}
β ő≤ -->
(
x
)
=
x
− ‚ąí -->
A
B
− ‚ąí -->
A
{\displaystyle \beta (x)={\frac {x-A}{B-A}}}
α őĪ -->
(
x
)
=
B
− ‚ąí -->
x
B
− ‚ąí -->
A
{\displaystyle \alpha (x)={\frac {B-x}{B-A}}}
–í–Ķ–Ľ–ł—á–ł–Ĺ—č
α őĪ -->
(
x
)
{\displaystyle \alpha (x)}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
–≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ź–ľ–ł —Ä–į–∑–ĺ—Ä–Ķ–Ĺ–ł—Ź –Ņ–Ķ—Ä–≤–ĺ–≥–ĺ –ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –ł–≥—Ä–ĺ–ļ–į –Ņ—Ä–ł –Ĺ–į—á–į–Ľ—Ć–Ĺ—č—Ö –ļ–į–Ņ–ł—ā–į–Ľ–į—Ö
x
− ‚ąí -->
A
{\displaystyle x-A}
B
− ‚ąí -->
x
{\displaystyle B-x}
ξ őĺ -->
i
=
+
1
{\displaystyle \xi _{i}=+1}
ξ őĺ -->
i
=
− ‚ąí -->
1
{\displaystyle \xi _{i}=-1}
–ē—Ā–Ľ–ł
A
=
0
{\displaystyle A=0}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
x
{\displaystyle x}
B
{\displaystyle B}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
β ő≤ -->
(
x
)
=
{
x
B
,
p
=
q
=
0
,
5
,
(
q
p
)
x
− ‚ąí -->
1
(
q
p
)
B
− ‚ąí -->
1
,
p
≠ ‚Ȇ -->
q
{\displaystyle \beta (x)={\begin{cases}{\frac {x}{B}},&p=q=0{,}5,\\{\frac {\left({\frac {q}{p}}\right)^{x}-1}{\left({\frac {q}{p}}\right)^{B}-1}},&p\neq q\end{cases}}}
–ß—ā–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ —Ā–ī–Ķ–Ľ–į—ā—Ć –Ņ–Ķ—Ä–≤–ĺ–ľ—É –ł–≥—Ä–ĺ–ļ—É, –Ķ—Ā–Ľ–ł –ł–≥—Ä–į –Ĺ–Ķ–Ī–Ľ–į–≥–ĺ–Ņ—Ä–ł—Ź—ā–Ĺ–į –ī–Ľ—Ź –Ĺ–Ķ–≥–ĺ?
–ē–≥–ĺ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć –Ņ—Ä–ĺ–ł–≥—Ä—č—ą–į –∑–į–ī–į–Ĺ–į —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ
lim
k
→ ‚Üí -->
∞ ‚ąě -->
α őĪ -->
k
=
α őĪ -->
=
(
q
p
)
B
− ‚ąí -->
1
(
q
p
)
B
− ‚ąí -->
(
q
p
)
A
{\displaystyle \lim \limits _{k\rightarrow \infty }\alpha _{k}=\alpha ={\frac {\left({\frac {q}{p}}\right)^{B}-1}{\left({\frac {q}{p}}\right)^{B}-\left({\frac {q}{p}}\right)^{A}}}}
(
− ‚ąí -->
A
)
{\displaystyle (-A)}
P
(
{
ξ őĺ -->
i
=
2
}
)
=
p
{\displaystyle \mathbb {P} {\bigl (}\{\xi _{i}=2\}{\bigr )}=p}
P
(
{
ξ őĺ -->
i
=
− ‚ąí -->
2
}
)
=
q
{\displaystyle \mathbb {P} {\bigl (}\{\xi _{i}=-2\}{\bigr )}=q}
α őĪ -->
2
=
(
q
p
)
0
,
5
B
− ‚ąí -->
1
(
q
p
)
0
,
5
B
− ‚ąí -->
(
q
p
)
0
,
5
A
{\displaystyle \alpha _{2}={\frac {\left({\frac {q}{p}}\right)^{0{,}5B}-1}{\left({\frac {q}{p}}\right)^{0{,}5B}-\left({\frac {q}{p}}\right)^{0{,}5A}}}}
–ü–ĺ—ć—ā–ĺ–ľ—É
α őĪ -->
=
(
q
p
)
0
,
5
B
⋅ ‚čÖ -->
2
− ‚ąí -->
1
2
(
q
p
)
0
,
5
B
⋅ ‚čÖ -->
2
− ‚ąí -->
(
q
p
)
0
,
5
A
⋅ ‚čÖ -->
2
=
(
(
q
p
)
0
,
5
B
− ‚ąí -->
1
)
⋅ ‚čÖ -->
(
(
q
p
)
0
,
5
B
+
1
)
(
(
q
p
)
0
,
5
B
− ‚ąí -->
(
q
p
)
0
,
5
A
)
⋅ ‚čÖ -->
(
(
q
p
)
0
,
5
B
+
(
q
p
)
0
,
5
A
)
=
α őĪ -->
2
⋅ ‚čÖ -->
(
(
q
p
)
0
,
5
B
+
1
)
(
(
q
p
)
0
,
5
B
+
(
q
p
)
0
,
5
A
)
>
α őĪ -->
2
{\displaystyle \alpha ={\frac {\left({\frac {q}{p}}\right)^{0{,}5B\cdot 2}-1^{2}}{\left({\frac {q}{p}}\right)^{0{,}5B\cdot 2}-\left({\frac {q}{p}}\right)^{0{,}5A\cdot 2}}}={\frac {\left(\left({\frac {q}{p}}\right)^{0{,}5B}-1\right)\cdot \left(\left({\frac {q}{p}}\right)^{0{,}5B}+1\right)}{\left(\left({\frac {q}{p}}\right)^{0{,}5B}-\left({\frac {q}{p}}\right)^{0{,}5A}\right)\cdot \left(\left({\frac {q}{p}}\right)^{0{,}5B}+\left({\frac {q}{p}}\right)^{0{,}5A}\right)}}=\alpha _{2}\cdot {\frac {\left(\left({\frac {q}{p}}\right)^{0{,}5B}+1\right)}{\left(\left({\frac {q}{p}}\right)^{0{,}5B}+\left({\frac {q}{p}}\right)^{0{,}5A}\right)}}>\alpha _{2}}
α őĪ -->
2
{\displaystyle \alpha _{2}}
q
>
p
{\displaystyle q>p}
0
,
5
{\displaystyle 0{,}5}
r
>
1
{\displaystyle r>1}
B
{\displaystyle B}
B
{\displaystyle B}
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā—Ä–Ķ–ī–Ĺ—é—é –ī–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć –Ī–Ľ—É–∂–ī–į–Ĺ–ł—Ź –Ĺ–į—ą–Ķ–Ļ —á–į—Ā—ā–ł—Ü—č. –í–≤–Ķ–ī—Ď–ľ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ–∂–ł–ī–į–Ĺ–ł–Ķ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į, –ļ–ĺ–≥–ī–į –ł–≥—Ä–į –Ņ—Ä–Ķ–ļ—Ä–į—Č–į–Ķ—ā—Ā—Ź:
E
(
τ ŌĄ -->
k
x
)
=
m
k
(
x
)
{\displaystyle \mathbb {E} (\tau _{k}^{x})=m_{k}(x)}
k
⩽ ‚©Ĺ -->
n
{\displaystyle k\leqslant n}
m
k
(
x
)
=
E
(
τ ŌĄ -->
k
x
)
=
∑ ‚ąĎ -->
1
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
l
P
(
{
τ ŌĄ -->
k
x
=
l
}
)
=
∑ ‚ąĎ -->
1
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
l
(
p
P
(
{
τ ŌĄ -->
k
x
=
l
}
|
{
ξ őĺ -->
1
=
1
}
)
+
q
P
(
{
τ ŌĄ -->
k
x
=
l
}
|
{
ξ őĺ -->
1
=
− ‚ąí -->
1
}
)
)
=
{\displaystyle m_{k}(x)=\mathbb {E} (\tau _{k}^{x})=\sum \limits _{1\leqslant l\leqslant k}l\mathbb {P} {\bigl (}\{\tau _{k}^{x}=l\}{\bigr )}=\sum \limits _{1\leqslant l\leqslant k}l{\Bigl (}p\mathbb {P} {\bigl (}\{\tau _{k}^{x}=l\}{\big |}\{\xi _{1}=1\}{\bigr )}+q\mathbb {P} {\bigl (}\{\tau _{k}^{x}=l\}{\big |}\{\xi _{1}=-1\}{\bigr )}{\Bigr )}=}
=
∑ ‚ąĎ -->
1
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
l
(
p
P
(
{
τ ŌĄ -->
k
− ‚ąí -->
1
x
+
1
=
l
− ‚ąí -->
1
}
)
+
q
P
{
τ ŌĄ -->
k
− ‚ąí -->
1
x
− ‚ąí -->
1
=
l
− ‚ąí -->
1
}
)
)
=
∑ ‚ąĎ -->
0
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
− ‚ąí -->
1
(
l
+
1
)
(
p
P
(
{
τ ŌĄ -->
k
− ‚ąí -->
1
x
+
1
=
l
}
)
+
q
P
(
{
τ ŌĄ -->
k
− ‚ąí -->
1
x
− ‚ąí -->
1
=
l
}
)
)
=
{\displaystyle =\sum \limits _{1\leqslant l\leqslant k}l{\Bigl (}p\mathbb {P} {\bigl (}\{\tau _{k-1}^{x+1}=l-1\}{\bigr )}+q\mathbb {P} {\bigl \{}\tau _{k-1}^{x-1}=l-1\}{\bigr )}{\Bigr )}=\sum \limits _{0\leqslant l\leqslant k-1}(l+1){\Bigl (}p\mathbb {P} {\bigl (}\{\tau _{k-1}^{x+1}=l\}{\bigr )}+q\mathbb {P} {\bigl (}\{\tau _{k-1}^{x-1}=l\}{\bigr )}{\Bigr )}=}
=
p
m
k
− ‚ąí -->
1
(
x
+
1
)
+
q
m
k
− ‚ąí -->
1
(
x
− ‚ąí -->
1
)
+
∑ ‚ąĎ -->
0
⩽ ‚©Ĺ -->
l
⩽ ‚©Ĺ -->
k
− ‚ąí -->
1
(
p
P
(
{
τ ŌĄ -->
k
− ‚ąí -->
1
x
+
1
=
l
}
)
+
q
P
(
{
τ ŌĄ -->
k
− ‚ąí -->
1
x
− ‚ąí -->
1
=
l
}
)
)
=
p
m
k
− ‚ąí -->
1
(
x
+
1
)
+
q
m
k
− ‚ąí -->
1
(
x
− ‚ąí -->
1
)
+
1.
{\displaystyle =pm_{k-1}(x+1)+qm_{k-1}(x-1)+\sum \limits _{0\leqslant l\leqslant k-1}{\Bigl (}p\mathbb {P} {\bigl (}\{\tau _{k-1}^{x+1}=l\}{\bigr )}+q\mathbb {P} {\bigl (}\{\tau _{k-1}^{x-1}=l\}{\bigr )}{\Bigr )}=pm_{k-1}(x+1)+qm_{k-1}(x-1)+1.}
–Ē–Ľ—Ź
x
∈ ‚ąą -->
(
A
;
B
)
{\displaystyle x\in (A;B)}
k
∈ ‚ąą -->
[
0
;
n
]
{\displaystyle k\in [0;n]}
m
k
(
x
)
{\displaystyle m_{k}(x)}
m
k
(
x
)
=
p
m
k
− ‚ąí -->
1
(
x
+
1
)
+
q
m
k
− ‚ąí -->
1
(
x
− ‚ąí -->
1
)
+
1
{\displaystyle m_{k}(x)=pm_{k-1}(x+1)+qm_{k-1}(x-1)+1}
m
0
(
x
)
=
0
{\displaystyle m_{0}(x)=0}
A
{\displaystyle A}
B
{\displaystyle B}
m
k
(
A
)
=
m
k
(
B
)
=
0
{\displaystyle m_{k}(A)=m_{k}(B)=0}
m
i
(
x
)
{\displaystyle m_{i}(x)}
m
k
+
1
(
x
)
⩾ ‚©ĺ -->
m
k
(
x
)
{\displaystyle m_{k+1}(x)\geqslant m_{k}(x)}
m
(
x
)
=
lim
n
→ ‚Üí -->
∞ ‚ąě -->
m
n
(
x
)
{\displaystyle m(x)=\lim \limits _{n\rightarrow \infty }m_{n}(x)}
m
k
(
x
)
=
p
m
k
− ‚ąí -->
1
(
x
+
1
)
+
q
m
k
− ‚ąí -->
1
(
x
− ‚ąí -->
1
)
+
1
{\displaystyle m_{k}(x)=pm_{k-1}(x+1)+qm_{k-1}(x-1)+1}
m
(
x
)
=
1
+
p
m
(
x
+
1
)
+
q
m
(
x
− ‚ąí -->
1
)
{\displaystyle m(x)=1+pm(x+1)+qm(x-1)}
m
(
A
)
=
m
(
B
)
=
0
{\displaystyle m(A)=m(B)=0}
n
→ ‚Üí -->
∞ ‚ąě -->
{\displaystyle n\rightarrow \infty }
m
(
x
)
<
∞ ‚ąě -->
{\displaystyle m(x)<\infty }
x
∈ ‚ąą -->
(
A
;
B
)
{\displaystyle x\in (A;B)}
p
≠ ‚Ȇ -->
q
{\displaystyle p\neq q}
a
{\displaystyle a}
b
(
q
p
)
x
{\displaystyle b\left({\frac {q}{p}}\right)^{x}}
x
q
− ‚ąí -->
p
=
q
− ‚ąí -->
p
+
(
p
+
q
)
x
+
p
− ‚ąí -->
q
q
− ‚ąí -->
p
=
q
− ‚ąí -->
p
q
− ‚ąí -->
p
+
p
(
x
+
1
)
q
− ‚ąí -->
p
+
q
(
x
− ‚ąí -->
1
)
q
− ‚ąí -->
p
=
1
+
p
x
+
1
q
− ‚ąí -->
p
+
q
x
− ‚ąí -->
1
q
− ‚ąí -->
p
{\displaystyle {\frac {x}{q-p}}={\frac {q-p+(p+q)x+p-q}{q-p}}={\frac {q-p}{q-p}}+{\frac {p(x+1)}{q-p}}+{\frac {q(x-1)}{q-p}}=1+p{\frac {x+1}{q-p}}+q{\frac {x-1}{q-p}}}
m
(
x
)
=
x
q
− ‚ąí -->
p
+
a
+
b
(
q
p
)
x
{\displaystyle m(x)={\frac {x}{q-p}}+a+b\left({\frac {q}{p}}\right)^{x}}
m
(
A
)
=
m
(
B
)
=
0
{\displaystyle m(A)=m(B)=0}
m
(
x
)
{\displaystyle m(x)}
m
(
x
)
=
1
p
− ‚ąí -->
q
(
B
β ő≤ -->
(
x
)
+
A
α őĪ -->
(
x
)
− ‚ąí -->
x
)
{\displaystyle m(x)={\frac {1}{p-q}}{\bigl (}B\beta (x)+A\alpha (x)-x{\bigr )}}
m
(
x
)
=
a
+
b
x
− ‚ąí -->
x
2
{\displaystyle m(x)=a+bx-x^{2}}
m
(
x
)
=
(
B
− ‚ąí -->
x
)
(
x
− ‚ąí -->
A
)
{\displaystyle m(x)=(B-x)(x-A)}
m
(
0
)
=
B
2
{\displaystyle m(0)=B^{2}}
–ü—Ä–ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł–ł –≤—č—ą–Ķ—É–ļ–į–∑–į–Ĺ–Ĺ—č—Ö —Ą–ĺ—Ä–ľ—É–Ľ –Ņ–ĺ–ī—Ä–į–∑—É–ľ–Ķ–≤–į–Ľ–į—Ā—Ć –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā—Ć—é –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–∂–ł–ī–į–Ĺ–ł—Ź —á–ł—Ā–Ľ–į —Ö–ĺ–ī–ĺ–≤:
m
(
x
)
<
∞ ‚ąě -->
{\displaystyle m(x)<\infty }
–Ē–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ
m
(
x
)
<
∞ ‚ąě -->
∀ ‚ąÄ -->
A
,
B
{\displaystyle m(x)<\infty \quad \forall A,B}
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ
–Ē–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –ī–ĺ–ļ–į–∑–į—ā—Ć —ć—ā–ĺ –ī–Ľ—Ź —Ā–Ľ—É—á–į—Ź
x
=
0
{\displaystyle x=0}
x
≠ ‚Ȇ -->
0
{\displaystyle x\neq 0}
x
=
0
{\displaystyle x=0}
A
{\displaystyle A}
B
{\displaystyle B}
p
=
q
{\displaystyle p=q}
p
≠ ‚Ȇ -->
q
{\displaystyle p\neq q}
–ė—ā–į–ļ, —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć
S
0
;
1
;
… ‚Ķ -->
;
n
{\displaystyle S_{0;1;\ldots ;n}}
S
τ ŌĄ -->
n
=
S
τ ŌĄ -->
n
(
ω ŌČ -->
)
{\displaystyle S_{\tau _{n}}=S_{\tau _{n}}(\omega )}
τ ŌĄ -->
n
=
τ ŌĄ -->
n
0
{\displaystyle \tau _{n}=\tau _{n}^{0}}
–ü—É—Ā—ā—Ć
S
τ ŌĄ -->
n
(
ω ŌČ -->
)
=
∑ ‚ąĎ -->
k
=
0
n
S
k
(
ω ŌČ -->
)
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
{\displaystyle S_{\tau _{n}}(\omega )=\sum \limits _{k=0}^{n}S_{k}(\omega )\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega )}
S
τ ŌĄ -->
n
{\displaystyle S_{\tau _{n}}}
τ ŌĄ -->
n
{\displaystyle \tau _{n}}
τ ŌĄ -->
n
<
n
{\displaystyle \tau _{n}<n}
S
τ ŌĄ -->
n
∈ ‚ąą -->
{
A
;
B
}
{\displaystyle S_{\tau _{n}}\in \{A;B\}}
τ ŌĄ -->
n
=
n
{\displaystyle \tau _{n}=n}
A
⩽ ‚©Ĺ -->
S
τ ŌĄ -->
n
⩽ ‚©Ĺ -->
B
{\displaystyle A\leqslant S_{\tau _{n}}\leqslant B}
p
=
q
=
0
,
5
{\displaystyle p=q=0{,}5}
E
(
S
τ ŌĄ -->
n
)
=
0
{\displaystyle \mathbb {E} (S_{\tau _{n}})=0}
E
(
S
τ ŌĄ -->
n
2
)
=
E
(
τ ŌĄ -->
n
)
{\displaystyle \mathbb {E} (S_{\tau _{n}}^{2})=\mathbb {E} (\tau _{n})}
E
(
S
τ ŌĄ -->
n
)
=
∑ ‚ąĎ -->
k
=
0
n
E
(
S
k
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
=
∑ ‚ąĎ -->
k
=
0
n
E
(
S
n
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
+
∑ ‚ąĎ -->
k
=
0
n
(
(
S
k
− ‚ąí -->
S
n
)
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
=
E
(
S
n
)
+
∑ ‚ąĎ -->
k
=
0
n
(
(
S
k
− ‚ąí -->
S
n
)
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
{\displaystyle \mathbb {E} (S_{\tau _{n}})=\sum \limits _{k=0}^{n}\mathbb {E} {\bigl (}S_{k}\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}=\sum \limits _{k=0}^{n}\mathbb {E} {\bigl (}S_{n}\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}+\sum \limits _{k=0}^{n}{\bigl (}(S_{k}-S_{n})\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}=\mathbb {E} (S_{n})+\sum \limits _{k=0}^{n}{\bigl (}(S_{k}-S_{n})\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}}
E
(
S
n
)
=
0
{\displaystyle \mathbb {E} (S_{n})=0}
S
n
=
ξ őĺ -->
1
+
… ‚Ķ -->
+
ξ őĺ -->
n
{\displaystyle S_{n}=\xi _{1}+\ldots +\xi _{n}}
ξ őĺ -->
i
=
± ¬Ī -->
1
{\displaystyle \xi _{i}=\pm 1}
p
=
q
{\displaystyle p=q}
∑ ‚ąĎ -->
k
=
0
n
(
(
S
k
− ‚ąí -->
S
n
)
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
=
0
{\displaystyle \sum \limits _{k=0}^{n}{\bigl (}(S_{k}-S_{n})\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}=0}
–Ē–Ľ—Ź
0
⩽ ‚©Ĺ -->
k
<
n
{\displaystyle 0\leqslant k<n}
{
τ ŌĄ -->
n
>
k
}
=
{
A
<
S
1
<
B
;
… ‚Ķ -->
;
A
<
S
k
<
B
}
{\displaystyle \{\tau _{n}>k\}=\{A<S_{1}<B;\ldots ;A<S_{k}<B\}}
—Ā–ĺ–Ī—č—ā–ł–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ĺ –≤ –≤–ł–ī–Ķ
{
ω ŌČ -->
: : -->
(
ξ őĺ -->
1
;
… ‚Ķ -->
;
ξ őĺ -->
n
)
∈ ‚ąą -->
J
}
{\displaystyle {\bigl \{}\omega \colon (\xi _{1};\ldots ;\xi _{n})\in J{\bigr \}}}
J
{\displaystyle J}
–Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į
{
− ‚ąí -->
1
;
+
1
}
k
{\displaystyle \{-1;+1\}^{k}}
ξ őĺ -->
i
{\displaystyle \xi _{i}}
i
=
1
;
k
¯ ¬Į -->
{\displaystyle i={\overline {1;k}}}
i
{\displaystyle i}
ξ őĺ -->
k
+
1
;
… ‚Ķ -->
;
ξ őĺ -->
n
{\displaystyle \xi _{k+1};\ldots ;\xi _{n}}
J
{\displaystyle J}
{
τ ŌĄ -->
n
=
k
}
=
{
τ ŌĄ -->
n
>
k
− ‚ąí -->
1
}
∖ ‚ąĖ -->
{
τ ŌĄ -->
n
>
k
}
{\displaystyle \{\tau _{n}=k\}=\{\tau _{n}>k-1\}\backslash \{\tau _{n}>k\}}
{
ω ŌČ -->
: : -->
(
ξ őĺ -->
1
;
… ‚Ķ -->
;
ξ őĺ -->
n
)
∈ ‚ąą -->
J
}
{\displaystyle {\bigl \{}\omega \colon (\xi _{1};\ldots ;\xi _{n})\in J{\bigr \}}}
ξ őĺ -->
i
{\displaystyle \xi _{i}}
–Ņ–ĺ–ī–∑–į–ī–į—á–Ķ 2 ) –≤—č—ā–Ķ–ļ–į–Ķ—ā, —á—ā–ĺ
∀ ‚ąÄ -->
0
⩽ ‚©Ĺ -->
k
<
n
{\displaystyle \forall 0\leqslant k<n}
S
n
− ‚ąí -->
S
k
{\displaystyle S_{n}-S_{k}}
1
{
τ ŌĄ -->
n
=
k
}
{\displaystyle \mathbf {1} _{\{\tau _{n}=k\}}}
E
(
S
k
⋅ ‚čÖ -->
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
=
E
(
S
k
)
⋅ ‚čÖ -->
E
(
1
{
τ ŌĄ -->
n
=
k
}
(
ω ŌČ -->
)
)
=
0
{\displaystyle \mathbb {E} {\bigl (}S_{k}\cdot \mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}=\mathbb {E} (S_{k})\cdot \mathbb {E} {\bigl (}\mathbf {1} _{\{{\tau _{n}=k}\}}(\omega ){\bigr )}=0}
E
(
S
τ ŌĄ -->
n
2
)
=
∑ ‚ąĎ -->
k
=
0
n
E
(
S
k
2
1
{
τ ŌĄ -->
n
=
k
}
)
=
{\displaystyle \mathbb {E} (S_{\tau _{n}}^{2})=\sum \limits _{k=0}^{n}\mathbb {E} (S_{k}^{2}\mathbf {1} _{\{{\tau _{n}=k}\}})=}
=
∑ ‚ąĎ -->
k
=
0
n
E
(
(
S
n
+
(
S
k
− ‚ąí -->
S
n
)
2
)
1
{
τ ŌĄ -->
n
=
k
}
)
=
∑ ‚ąĎ -->
k
=
0
n
(
E
(
S
2
)
1
{
τ ŌĄ -->
n
=
k
}
+
2
E
(
S
n
(
S
k
− ‚ąí -->
S
n
)
)
1
{
τ ŌĄ -->
n
=
k
}
+
E
(
(
S
n
− ‚ąí -->
S
k
)
2
)
1
{
τ ŌĄ -->
n
=
k
}
)
=
{\displaystyle =\sum \limits _{k=0}^{n}\mathbb {E} {\Bigl (}{\bigl (}S_{n}+(S_{k}-S_{n})^{2}{\bigr )}\mathbf {1} _{\{{\tau _{n}=k}\}}{\Bigr )}=\sum \limits _{k=0}^{n}{\Bigl (}\mathbb {E} (S^{2})\mathbf {1} _{\{{\tau _{n}=k}\}}+2\mathbb {E} {\bigl (}S_{n}(S_{k}-S_{n}){\bigr )}\mathbf {1} _{\{{\tau _{n}=k}\}}+\mathbb {E} {\bigl (}(S_{n}-S_{k})^{2}{\bigr )}\mathbf {1} _{\{{\tau _{n}=k}\}}{\Bigr )}=}
=
E
(
S
2
)
− ‚ąí -->
∑ ‚ąĎ -->
k
=
0
n
E
(
(
S
n
− ‚ąí -->
S
k
)
2
)
1
{
τ ŌĄ -->
n
=
k
}
=
n
− ‚ąí -->
∑ ‚ąĎ -->
k
=
0
n
E
(
n
− ‚ąí -->
k
)
P
(
{
τ ŌĄ -->
n
=
k
}
)
=
∑ ‚ąĎ -->
k
=
0
n
k
P
(
{
τ ŌĄ -->
n
=
k
}
)
=
E
(
τ ŌĄ -->
n
)
.
{\displaystyle =\mathbb {E} (S^{2})-\sum \limits _{k=0}^{n}\mathbb {E} {\bigl (}(S_{n}-S_{k})^{2}{\bigr )}\mathbf {1} _{\{{\tau _{n}=k}\}}=n-\sum \limits _{k=0}^{n}\mathbb {E} (n-k)\mathbb {P} {\bigl (}\{\tau _{n}=k\}{\bigr )}=\sum \limits _{k=0}^{n}k\mathbb {P} {\bigl (}\{\tau _{n}=k\}{\bigr )}=\mathbb {E} (\tau _{n}).}
–£—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ĺ, —á—ā–ĺ –ī–Ľ—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ľ–ĺ–Ĺ–Ķ—ā–ļ–ł
E
(
S
τ ŌĄ -->
n
)
=
0
{\displaystyle \mathbb {E} (S_{\tau _{n}})=0}
E
(
S
τ ŌĄ -->
n
2
)
=
E
(
τ ŌĄ -->
n
)
{\displaystyle \mathbb {E} (S_{\tau _{n}}^{2})=\mathbb {E} (\tau _{n})}
–í —Ā–Ľ—É—á–į–Ķ –∂–Ķ
p
≠ ‚Ȇ -->
q
{\displaystyle p\neq q}
E
(
S
τ ŌĄ -->
n
)
=
(
p
− ‚ąí -->
q
)
E
(
τ ŌĄ -->
n
)
{\displaystyle \mathbb {E} (S_{\tau _{n}})=(p-q)\mathbb {E} (\tau _{n})}
E
(
ξ őĺ -->
1
)
=
p
− ‚ąí -->
q
{\displaystyle \mathbb {E} (\xi _{1})=p-q}
E
(
(
S
τ ŌĄ -->
n
− ‚ąí -->
τ ŌĄ -->
n
E
(
ξ őĺ -->
1
)
)
2
)
=
V
a
r
(
ξ őĺ -->
1
)
⋅ ‚čÖ -->
E
(
τ ŌĄ -->
n
)
{\displaystyle \mathbb {E} {\Bigl (}{\bigl (}S_{\tau _{n}}-\tau _{n}\mathbb {E} (\xi _{1}){\bigr )}^{2}{\Bigr )}=\mathrm {Var} (\xi _{1})\cdot \mathbb {E} (\tau _{n})}
V
a
r
(
ξ őĺ -->
1
)
=
1
− ‚ąí -->
(
p
− ‚ąí -->
q
)
2
{\displaystyle \mathrm {Var} (\xi _{1})=1-(p-q)^{2}}
lim
n
→ ‚Üí -->
∞ ‚ąě -->
m
n
(
0
)
=
m
(
0
)
<
∞ ‚ąě -->
{\displaystyle \lim \limits _{n\rightarrow \infty }m_{n}(0)=m(0)<\infty }
–í —Ā–Ľ—É—á–į–Ķ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ–Ļ –ł–≥—Ä—č –≤ —Ā–ł–Ľ—É —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź
E
(
S
τ ŌĄ -->
n
2
)
=
E
(
τ ŌĄ -->
n
)
{\displaystyle \mathbb {E} (S_{\tau _{n}}^{2})=\mathbb {E} (\tau _{n})}
E
(
τ ŌĄ -->
n
)
⩽ ‚©Ĺ -->
max
{
A
2
;
B
2
}
{\displaystyle \mathbb {E} (\tau _{n})\leqslant \max\{A^{2};B^{2}\}}
E
(
τ ŌĄ -->
n
)
=
E
(
S
τ ŌĄ -->
n
2
)
=
A
2
α őĪ -->
n
+
B
2
β ő≤ -->
n
+
E
(
S
n
2
1
{
A
<
S
n
<
B
}
)
1
{
τ ŌĄ -->
n
=
n
}
{\displaystyle \mathbb {E} (\tau _{n})=\mathbb {E} (S_{\tau _{n}}^{2})=A^{2}\alpha _{n}+B^{2}\beta _{n}+\mathbb {E} (S_{n}^{2}\mathbf {1} _{\{{A<S_{n}<B}\}})\mathbf {1} _{\{{\tau _{n}=n}\}}}
A
2
α őĪ -->
n
+
B
2
β ő≤ -->
n
⩽ ‚©Ĺ -->
E
(
τ ŌĄ -->
n
)
⩽ ‚©Ĺ -->
A
2
α őĪ -->
n
+
B
2
β ő≤ -->
n
+
max
{
A
2
;
B
2
}
⋅ ‚čÖ -->
γ ő≥ -->
n
{\displaystyle A^{2}\alpha _{n}+B^{2}\beta _{n}\leqslant \mathbb {E} (\tau _{n})\leqslant A^{2}\alpha _{n}+B^{2}\beta _{n}+\max\{A^{2};B^{2}\}\cdot \gamma _{n}}
γ ő≥ -->
n
<
ε őĶ -->
n
{\displaystyle \gamma _{n}<\varepsilon ^{n}}
E
(
τ ŌĄ -->
n
)
{\displaystyle \mathbb {E} (\tau _{n})}
n
→ ‚Üí -->
∞ ‚ąě -->
{\displaystyle n\rightarrow \infty }
m
(
0
)
=
A
2
α őĪ -->
+
B
2
β ő≤ -->
=
A
2
⋅ ‚čÖ -->
B
B
− ‚ąí -->
A
− ‚ąí -->
B
2
⋅ ‚čÖ -->
A
B
− ‚ąí -->
A
=
|
A
B
|
{\displaystyle m(0)=A^{2}\alpha +B^{2}\beta =A^{2}\cdot {\frac {B}{B-A}}-B^{2}\cdot {\frac {A}{B-A}}=|AB|}
E
(
τ ŌĄ -->
n
)
⩽ ‚©Ĺ -->
max
{
|
A
|
;
B
}
|
p
− ‚ąí -->
q
|
{\displaystyle \mathbb {E} (\tau _{n})\leqslant {\frac {\max\{|A|;B\}}{|p-q|}}}
τ ŌĄ -->
n
{\displaystyle \tau _{n}}
E
(
τ ŌĄ -->
n
)
→ ‚Üí -->
m
(
0
)
=
α őĪ -->
A
+
β ő≤ -->
B
p
− ‚ąí -->
q
{\displaystyle \mathbb {E} (\tau _{n})\rightarrow m(0)={\frac {\alpha A+\beta B}{p-q}}}
◼ ‚óľ -->
{\displaystyle \blacksquare }
–Ē–Ľ—Ź –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –ł–≥—Ä—č –≤–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–ĺ–Ļ MATLAB .
–Ē–Ľ—Ź –Ĺ–į—á–į–Ľ–į —Ā–≥–Ķ–Ĺ–Ķ—Ä–ł—Ä—É–Ķ–ľ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć
ξ őĺ -->
i
{\displaystyle \xi _{i}}
x
{\displaystyle x}
S
k
{\displaystyle S_{k}}
őĺ (getXI)n = 100 ; % The length of \xi_i series
U = rand ( n , 1 ); % Generate 100 random uniform [0;1] values
XI = zeros ( n , 1 ); % Reserve memory for 100 modified Bernoulli
q = 0.55 ; % Reverse probability
p = 1 - q ; % Averse probability
% The following cycle creates a Bernoulli distribution based on uniform [0;1]
for i = 1 : n % This cycle divides the [0;1] array into 2 parts: lengths q and p, q+p=1
if ( U ( i , 1 ) < q )
XI ( i , 1 ) = - 1 ; % If a uniform random value falls into q then \xi=-1
else XI ( i , 1 ) = 1 ; % If a uniform random value falls into p then \xi=+1
end
end
x = 10 ; % Initial 1st player's budget offset
S = zeros ( n , 1 ); % Reserve memory for 100 S_1...S_100
for i = 1 : n % Make S_k series according to rule S_{k+1} = S_k + \xi_{k+1}
S ( i , 1 ) = x + sum ( XI ( 1 : i , 1 )); % considering the initial welfare offset x
end
–ó–į—ā–Ķ–ľ –≤–≤–Ķ–ī—Ď–ľ —Ą—É–Ĺ–ļ—Ü–ł—é getS(n, q, x) , –ļ–ĺ—ā–ĺ—Ä–į—Ź –Ī—č –Ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ, –ļ–į–ļ –Ľ–ł—Ā—ā–ł–Ĺ–≥ –≤—č—ą–Ķ, –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–ĺ–≤–į–Ľ–į —Ä—Ź–ī
S
k
{\displaystyle S_{k}}
n
{\displaystyle n}
q
{\displaystyle q}
x
{\displaystyle x}
function [S] = getS ( n, q, x) % This function depends on n, q and x --- 3 variables
U = rand ( n , 1 );
XI = zeros ( n , 1 );
for i = 2 : n % Uniform->Bernoulli distribution transformation
if ( U ( i , 1 ) < q )
XI ( i , 1 ) = - 1 ;
else XI ( i , 1 ) = 1 ;
end
end
S = zeros ( n , 1 ); % Reserve memory for n S_1...S_n
for i = 2 : n % Calculate the S_1...S_n series
S ( i , 1 ) = sum ( XI ( 1 : i , 1 )); % Sums the \xi's
end
S = x + S ; % Adds initial welfare to each S_k of the whole matrix
–í–ĺ–∑–Ĺ–ł–ļ–į–Ķ—ā —Ä–į–∑—É–ľ–Ĺ—č–Ļ –≤–ĺ–Ņ—Ä–ĺ—Ā: –∑–į—á–Ķ–ľ —Ā—á–ł—ā–į—ā—Ć
ξ őĺ -->
{\displaystyle \xi }
for i = 2:n )? –Ē–Ķ–Ľ–ĺ –≤ —ā–ĺ–ľ, —á—ā–ĺ —ć—ā–ĺ –ī–Ķ–Ľ–į–Ķ—ā—Ā—Ź –ł—Ā–ļ–Ľ—é—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤ —Ü–Ķ–Ľ—Ź—Ö –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ–Ļ –≤–ł–∑—É–į–Ľ–ł–∑–į—Ü–ł–ł. –ü—Ä–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –≥—Ä–į—Ą–ł–ļ–į –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ –ļ–ĺ–ī–Ķ –Ī—É–ī—É—ā —Ā—ā—Ä–ĺ–ł—ā—Ć—Ā—Ź —ā—Ä–į–Ķ–ļ—ā–ĺ—Ä–ł–ł
S
k
{\displaystyle S_{k}}
for i = 1:n , —ā–ĺ —ā–ĺ–≥–ī–į —É–∂–Ķ —Ā —Ā–į–ľ–ĺ–≥–ĺ –Ņ–Ķ—Ä–≤–ĺ–≥–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ —ā—Ä–į–Ķ–ļ—ā–ĺ—Ä–ł–ł –Ī—č –≤—č—Ö–ĺ–ī–ł–Ľ–ł –ł–∑
x
− ‚ąí -->
1
{\displaystyle x-1}
x
+
1
{\displaystyle x+1}
ξ őĺ -->
1
{\displaystyle \xi _{1}}
–Ę—Ä–ł –ł–≥—Ä—č –≤ 10 —ą–į–≥–ĺ–≤ –Ņ—Ä–ł
q
=
0
,
45
{\displaystyle q=0{,}45}
–ü—Ź—ā—Ć –ł–≥—Ä –≤ 100 —ą–į–≥–ĺ–≤ –Ņ—Ä–ł
q
=
0
,
56
{\displaystyle q=0{,}56}
A
{\displaystyle A}
–°—ā–ĺ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤—č—Ö –ł–≥—Ä –≤ 10000 —ą–į–≥–ĺ–≤. N = 3 ; % Number of games played
n = 10 ; % Number of tosses
q = 0.45 ; % Chance 1st player loses 1 rouble
x = 0 ; % Initial welfare offset
matrS = zeros ( N , n ); % Reserve memory for N rows n cols matrix
for i = 1 : N % This loop fills the S matrix with S_k, yielding N trajectories
matrS ( i ,:) = getS ( n , q , x ) ' ;
plot ( matrS ( i ,:)); % Gives an image
hold on ; % Holds the axes for next trajectory overlay
end
hold off ; % Clears axes for a new plot
–Ę–Ķ–Ņ–Ķ—Ä—Ć –Ņ–ĺ–ī–ĺ–Ļ–ī—Ď–ľ –ļ —Ā–į–ľ–ĺ–Ļ –≥–Ľ–į–≤–Ĺ–ĺ–Ļ —Ā–ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–Ķ–Ļ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–Ĺ–ĺ–Ļ —á–į—Ā—ā–ł ‚ÄĒ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—É, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ–ĺ–∑–≤–ĺ–Ľ–ł–Ľ –Ī—č –≤—č—á–ł—Ā–Ľ—Ź—ā—Ć —Ā—Ä–Ķ–ī–Ĺ—é—é –ī–Ľ–ł–Ĺ—É –ł–≥—Ä—č –Ņ—Ä–ł –∑–į–ī–į–Ĺ–Ĺ—č—Ö –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į—Ö
(
A
;
B
;
n
;
q
)
{\displaystyle (A;B;n;q)}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
N = 3000 ; % Number of games played
n = 3000 ; % Number of tosses
q = 0.5 ; % Chance 1st player loses 1 rouble
p = 1 - q ; % Chance 1st player wins 1 rouble
A = - 10 ; % 1st player budget
B = 10 ; % 2nd player budget
x = 0 ; % Budget offset towards 1st player
Bs = 0 ; % amount of cases particle hits B (it will change soon)
As = 0 ; % amount of cases particle hits A (it will change soon)
matrS = zeros ( N , n ); % Reserve memory for N rows n cols matrix
TAU1 = n * ones ( N , n ); % Fill another N rows n cols matrix with n's
for i = 1 : N % This loop makes up N trajectories of S_k relying on input q, x, n
matrS ( i ,:) = getS ( n , q , x ) ' ;
for j = 1 : n
if ( matrS ( i , j ) == A ) || ( matrS ( i , j ) == B ) % If a particle exceeds A or B, then
TAU1 ( i , j ) = j ; % put the number of step into the table
end
end
plot ( matrS ( i ,:)); % Displays a figure
grid on ;
hold on ; % Simultaneous plots within same axes
end
hold off ; % Clears axes for a new plot
TAU = ( min ( TAU1 ' )) ' ; % TAU = earliest step of [A;B] corridor overrun
% As [min] affects columns and gives row then we transpose TAU1,
% minimize it by rows and make it a column again
for i = 1 : N % Our S_n series are ready; they nest in matrS
for j = 1 : TAU ( i ) % Scan only till we encounter the escape step!
if ( matrS ( i , j ) == A ); % If a particle escaped through A (1st player busted)
As = As + 1 ; % then add +1 to 1st player's failures
elseif ( matrS ( i , j ) == B ) % Otherwise if its first threshold was B
Bs = Bs + 1 ; % then add +1 to 1st player's wins
end % If n is not large enough, then
end % As + Bs may not make up N
end
ALPHA = As / ( As + Bs ) % Match alphas with their theoretical values
if ( q == p )
THEORALPHA = ( B - x ) / ( B - A )
else THEORALPHA = (( q / p ) ^B - ( q / p ) ^x ) / (( q / p ) ^B - ( q / p ) ^A )
end
BETA = 1 - ALPHA % Same for betas
if ( q == p )
THEORBETA = ( x - A ) / ( B - A )
else THEORBETA = 1 - THEORALPHA
end
meanTAU = mean ( TAU ) % Law of large numbers for great N's
if ( q == p )
THEORTAU = ( B - x ) * ( x - A )
else THEORTAU = 1 / ( p - q ) * ( B * THEORBETA + A * THEORALPHA - x )
end
–ě—ā–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ –Ņ—Ä–ł –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ł—Ö
n
{\displaystyle n}
n
{\displaystyle n}
β ő≤ -->
n
(
x
)
{\displaystyle \beta _{n}(x)}
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
–Ě–ł–∂–Ķ—Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ī–į–Ĺ–Ĺ—č–Ķ —Ä–į—Ā—Ā—á–ł—ā–į–Ĺ—č –ī–Ľ—Ź
n
=
3000
{\displaystyle n=3000}
N
=
3000
{\displaystyle N=3000}
‚ĄĖ —ā–Ķ—Ā—ā–į
q
{\displaystyle q}
A
{\displaystyle A}
B
{\displaystyle B}
x
{\displaystyle x}
ALPHA
α őĪ -->
(
x
)
{\displaystyle \alpha (x)}
BETA
β ő≤ -->
(
x
)
{\displaystyle \beta (x)}
meanTAU
m
(
x
)
{\displaystyle m(x)}
1
0
,
49
{\displaystyle 0{,}49}
− ‚ąí -->
6
{\displaystyle -6}
5
{\displaystyle 5}
0
{\displaystyle 0}
0,402
0
{\displaystyle 0{,}4020}
0,400
6
{\displaystyle 0{,}4006}
0,598
0
{\displaystyle 0{,}5980}
0,599
4
{\displaystyle 0{,}5994}
30,930
7
{\displaystyle 30{,}9307}
29,685
6
{\displaystyle 29{,}6856}
2
0
,
6
{\displaystyle 0{,}6}
− ‚ąí -->
60
{\displaystyle -60}
6
{\displaystyle 6}
− ‚ąí -->
3
{\displaystyle -3}
0,973
3
{\displaystyle 0{,}9733}
0,974
0
{\displaystyle 0{,}9740}
0,026
7
{\displaystyle 0{,}0267}
0,026
0
{\displaystyle 0{,}0260}
278,220
0
{\displaystyle 278{,}2200}
276,415
9
{\displaystyle 276{,}4159}
3
0
,
6
{\displaystyle 0{,}6}
− ‚ąí -->
20
{\displaystyle -20}
2
{\displaystyle 2}
− ‚ąí -->
1
{\displaystyle -1}
0,704
0
{\displaystyle 0{,}7040}
0,703
8
{\displaystyle 0{,}7038}
0,296
0
{\displaystyle 0{,}2960}
0,296
2
{\displaystyle 0{,}2962}
62,268
0
{\displaystyle 62{,}2680}
62,417
8
{\displaystyle 62{,}4178}
4
0
,
54
{\displaystyle 0{,}54}
− ‚ąí -->
10
{\displaystyle -10}
50
{\displaystyle 50}
10
{\displaystyle 10}
0,999
0
{\displaystyle 0{,}9990}
0,998
4
{\displaystyle 0{,}9984}
0,001
0
{\displaystyle 0{,}0010}
0,001
6
{\displaystyle 0{,}0016}
251,358
7
{\displaystyle 251{,}3587}
248,820
5
{\displaystyle 248{,}8205}
5
0
,
5
{\displaystyle 0{,}5}
− ‚ąí -->
10
{\displaystyle -10}
20
{\displaystyle 20}
0
{\displaystyle 0}
0,658
0
{\displaystyle 0{,}6580}
0,666
7
{\displaystyle 0{,}6667}
0,342
0
{\displaystyle 0{,}3420}
0,333
3
{\displaystyle 0{,}3333}
202,300
7
{\displaystyle 202{,}3007}
200,000
0
{\displaystyle 200{,}0000}
6
0
,
35
{\displaystyle 0{,}35}
− ‚ąí -->
3
{\displaystyle -3}
90
{\displaystyle 90}
0
{\displaystyle 0}
0,145
7
{\displaystyle 0{,}1457}
0,156
1
{\displaystyle 0{,}1561}
0,854
3
{\displaystyle 0{,}8543}
0,843
9
{\displaystyle 0{,}8439}
256,455
7
{\displaystyle 256{,}4557}
251,602
2
{\displaystyle 251{,}6022}
–í —ć–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–į—Ö 2 –ł 3 –Ņ—Ä–ĺ–ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–ĺ–≤–į–Ĺ–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ: –Ķ—Ā–Ľ–ł –ł–≥—Ä–į –Ņ—Ä–ĺ–ł–≥—Ä—č—ą–Ĺ–į—Ź –ī–Ľ—Ź –Ņ–Ķ—Ä–≤–ĺ–≥–ĺ –ł–≥—Ä–ĺ–ļ–į, —ā–ĺ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ —Ā—ā–į–≤–ļ–ł –≤ –ľ–ĺ–ī–Ķ–Ľ–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ —Ā–ĺ–ļ—Ä–į—Č–Ķ–Ĺ–ł—é
A
{\displaystyle A}
B
{\displaystyle B}
x
{\displaystyle x}
B
{\displaystyle B}
























![{\displaystyle [A;B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c910a242e021416372826b01afe03be9ccd430)






























![{\displaystyle x\in \mathbb {Z} \cap [A;B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf8f3e1e424a1885ad730ecddccdff90005ec6c)






![{\displaystyle x\in [A;B]\cap \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bda111a6ea1078c14bba201f064d6d3c1d03648)









![{\displaystyle [0;k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c13eeab2d82544ad9bde929150f75a084885651c)







































![{\displaystyle l\in [0;n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5ddd4d02bc75c0cd9006e6164d77d07fc71229b)



































































![{\displaystyle \forall p\in [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/965582d4c46896b7c93f6cc7cda6e8d11761c91f)




















![{\displaystyle p\in [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91a2f4192860c4812bbe1c190645bfb14cc501ea)




















![{\displaystyle k\in [0;n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70456940ea7f8ca7d74a3edeb229d7bdf83053da)