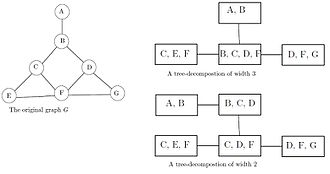
Древесная декомпозиция
|
Read other articles:

?Атериноїдні Атерина середземноморська (Atherina hepsetus) Біологічна класифікація Домен: Ядерні (Eukaryota) Царство: Тварини (Animalia) Тип: Хордові (Chordata) Клас: Променепері (Actinopterygii) Підклас: Новопері (Neopterygii) Інфраклас: Костисті риби (Teleostei) Надряд: Акантопері (Acanthopterygii) Percomorpha...

Nota: Para outras cidades contendo este nome, veja Sauce. El Sauce Município Localização El Sauce Coordenadas 13° 40' 8 N 87° 48' 2 O País El Salvador Departamento La Unión El Sauce é um município localizado no departamento de La Unión, em El Salvador. Referências Instituto Geográfico Nacional (1986). Diccionario Geográfico de El Salvador, Tomo I, A-K. San Salvador: Talleres Litográficos del Instituto Geográfico Nacional Porta...

Die COVID-19-Pandemie in Honduras tritt als regionales Teilgeschehen des weltweiten Ausbruchs der Atemwegserkrankung COVID-19 auf und beruht auf Infektionen mit dem Ende 2019 neu aufgetretenen Virus SARS-CoV-2 aus der Familie der Coronaviren. Die COVID-19-Pandemie breitet sich seit Dezember 2019 von China ausgehend aus.[1] Ab dem 11. März 2020 stufte die Weltgesundheitsorganisation (WHO) das Ausbruchsgeschehen des neuartigen Coronavirus als Pandemie ein.[2] Inhaltsverzeichnis...

Japanese anime television series Terror in ResonanceKey visual of the series残響のテロル(Zankyō no Teroru)GenrePsychological thriller[1]Created byShinichirō Watanabe Anime television seriesDirected byShinichirō WatanabeAssistant:Yuzuru TachikawaProduced byKoji YamamotoMakoto KimuraTakamitsu InoueWritten byShōten YanoHiroshi SekoJun KumagaiKenta IharaMusic byYoko KannoStudioMAPPALicensed byAUS: Madman EntertainmentNA: CrunchyrollUK: Anime Limited...

У Вікіпедії є статті про інші значення цього терміна: Седан (значення). «Седан» Повна назва Club Sportif Sedan Ardennes Прізвисько кабани, зелено-червоні Засновано 1919 Населений пункт Седан, Франція Стадіон «Луї Дюґоґез» Вміщує 23 189 Президент Марк Дюбуа Головний тренер Грегорі Пуар...

Labastide Entidad subnacional Escudo LabastideLocalización de Labastide en Francia Coordenadas 43°02′09″N 0°21′11″E / 43.035833333333, 0.35305555555556Entidad Comuna de Francia • País Francia • Región Mediodía-Pirineos • Departamento Altos Pirineos • Distrito distrito de Bagnères-de-Bigorre • Cantón cantón de Barthe-de-Neste • Mancomunidad Communauté de communes Neste BaronniesAlcalde Jean-Pierre Duthu(2008 - 20...

Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути піддано сумніву та вилучено. (жовтень 2014) Об'єднані сили «Північна Європа» Allied Forces Northern Europe На службі 1952 —...

Kaledonia BaruNouvelle-Calédonie (Prancis) Bendera Lambang Semboyan: Terre de parole, terre de partage(Prancis: Tanah untuk berbicara, tanah untuk berbagi)[1]Lagu kebangsaan: Soyons unis, devenons frères [1]Ibu kota(dan kota terbesar)Nouméa22°16′S 166°28′E / 22.267°S 166.467°E / -22.267; 166.467Bahasa resmiPrancisPemerintahanJajahan sui generis• Presiden Prancis Emmanuel Macron• Presiden Pemerintah Kaledonia Baru ...

Pertempuran SurabayaBagian dari Revolusi Nasional IndonesiaTentara India Britania menembaki penembak runduk Indonesia di balik tank Indonesia dalam pertempuran di Surabaya, November 1945.Tanggal27 Oktober – 20 November 1945(3 minggu dan 3 hari)LokasiSurabaya, IndonesiaHasil Britania menang secara militer/taktis. Indonesia menang secara strategis, politik, dan psikologis. Britania perlahan berhenti membantu Belanda mendirikan kembali koloninya di Indonesia dan menjadi netra...

Kathedrale Basiliek van de Heilige Familie Plaats Nairobi Denominatie Rooms-katholiek Coördinaten 1° 17′ NB, 36° 49′ OL Gebouwd in afgerond in 1963 Architectuur Architect(en) Dorothy Hughes Kerkprovincie Aartsbisdom Nairobi Portaal Christendom De Kathedrale Basiliek van de Heilig Familie (Engels: Cathedral Basilica of the Holy Family) is de belangrijkste rooms-katholieke kerk in de Keniaanse hoofdstad Nairobi, gelegen aan het City Square. Het is de zetel van d...

Debut single album by D-Crunch 0806Single album by D-CrunchReleasedAugust 6, 2018 (2018-08-06)GenreHip hopLength12:43LanguageKoreanLabelAll-S CompanyKakao MProducerLee Jong-seok (exec.), RenzieeD-Crunch chronology 0806(2018) M1112 (4colors)(2018) Singles from 0806 PalaceReleased: August 6, 2018 0806 is the debut single album by South Korean idol group D-Crunch. It was released on August 6, 2018, by All-S Company and distributed by Kakao M. The group contributed to the lyric...

Untuk bentuk yang terseksualisasi dari seragam sekolah perempuan Jepang, lihat Kogal. Sebuah fuku pelaut (luaran pelaut) musim dingin dengan bawahan panjang. Seragam sekolah Jepang dirancang berdasarkan pada seragam angkatan laut bergaya Eropa dan pertama kali digunakan di Jepang pada akhir abad ke-19, menggantikan Kimono.[1] Sekarang, seragam sekolah tersebut umumnya dipakai di berbagai sistem publik dan sekolah swasta di Jepang. Kata Jepang untuk jenis seragam ini adalah seifuku (�...

Epithelial layer of the seminiferous tubules Germinal epithelium (male)Germinal epithelium of the testicle. 1 basal lamina, 2 spermatogonia, 3 spermatocyte 1st order, 4 spermatocyte 2nd order, 5 spermatid, 6 mature spermatid, 7 Sertoli cell, 8 tight junction (blood testis barrier)IdentifiersMeSHD012670Anatomical terminology[edit on Wikidata] This article is part of a series onEpithelia Squamous epithelial cell Simple Stratified Columnar epithelial cell Simple Stratified Pseudostratified C...

Israeli children's channel This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nickelodeon Israel – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove this template message) Television channel NickelodeonLogo used since 2023[a]CountryIsraelBroadcast areaNationwideH...

Keighley & Kendal RoadKeighley and Kendal TurnpikeRoute informationLength54 mi (87 km)Existed1753–1878Major junctionsEast endKeighley 53°52′01″N 1°54′40″W / 53.867°N 1.911°W / 53.867; -1.911Major intersectionsSkipton - Addingham Turnpike Skipton - Colne Turnpike Kirkby Lonsdale - Milnthorpe TurnpikeWest endKendal 54°19′34″N 2°44′42″W / 54.326°N 2.745°W / 54.326; -2.745 LocationCountryUnited ...

Syrian politician (born 1960) HEHassan al-Nouriحسن النوريHassan al-Nouri in June 2014Minister of Administrative DevelopmentIn office27 August 2014 – 29 March 2017PresidentBashar al-AssadPrime MinisterWael al-HalqiImad KhamisPreceded byPosition establishedSucceeded bySalam SafafLeader of NIACSIncumbentAssumed office 2012Preceded byPosition establishedMember of the People's AssemblyIn office1998–2003PresidentHafez al-AssadBashar al-Assad Personal detailsBorn (1960-09-0...

WWII war crime by Nazi SS soldiers in France 50°35′42″N 2°38′52″E / 50.59500°N 2.64778°E / 50.59500; 2.64778 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Le Paradis massacre – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove this tem...

Nigerian shopkeeper and activist Grace Eniola SoyinkaBornGrace Eniola Jenkins-Harrison1908Died1983NationalityNigerianOccupation(s)Women's rights activistbusinesspersonSpouseSamuel Ayodele SoyinkaChildren7, including Wole SoyinkaRelativesFunmilayo Ransome-Kuti (aunt-in-law) Grace Eniola Soyinka (née Jenkins-Harrison) (1908–1983[1]) was a Nigerian shopkeeper, activist and member of the aristocratic Ransome-Kuti family.[2][3] She co-founded the Abeokuta Women’s ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يناير 2022) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

FleetwayPerusahaan indukEgmont PublishingDidirikan1890PendiriAlfred HarmsworthNegara asalInggrisKantor pusatFleetway HouseJenis terbitanMajalahGenre fiksiSci-fi, humor, petualangan Fleetway adalah sebuah perusahaan penerbis Inggris yang memproduksi komik-komik Inggris. Fleetway juga pernah menerbitkan komik Donal Bebek di Inggris. Artikel bertopik perusahaan ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs Artikel rintisan ini tidak memiliki kategori.Tolon...