3-3 дуопризма

3-3 дуопризма Диаграмма Шлегеля
Type	Однородная дуопризма
Символ Шлефли	{3}×{3} = {3}^2
Диаграммы Коксетера — Дынкина
Ячеек	6 треугольных призм
Граней	9 квадратов, 6 треугольников
Рёбер	18
Вершин	9
Вершинная фигура	Равногранный тетраэдр
Симметрия^[англ.]	[[3,2,3]] = [6,2^+,6], order 72
Двойственный	3-3 дуопирамида^[англ.]
Свойства	выпуклый, вершинно однородный, гранетранзитивный

3-3 дуопризма или треугольная дуопризма, наименьшая из p-q дуопризм, это четырёхмерный многогранник, получающийся прямым произведением двух треугольников.

Многогранник имеет 9 вершин, 18 рёбер, 15 граней (9 квадратов и 6 треугольников) в 6 ячейках в форме треугольных призм. Он имеет диаграмму Коксетера и симметрию [[3,2,3]] порядка 72. Его вершины и рёбра образуют ${\displaystyle 3\times 3}$ ладейный граф.

Гиперобъём

Гиперобъём однородной^[англ.] 3-3 дуопризмы с рёбрами длины a равен ${\displaystyle V_{4}={3 \over 16}a^{4}}$. Он вычисляется как квадрат площади правильного треугольника, ${\displaystyle A={{\sqrt {3}} \over 4}a^{2}}$.

Изображения

Ортогональные проекции

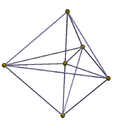
Развёртка	Вершинная перспектива	3D перспективная проекция с 2 различными вращениями

Симметрия

В 5-мерных пространствах некоторые однородные многогранники^[англ.] имеют 3-3 дуопризму в качестве вершинных фигур, некоторые с неравными длинами рёбер, а потому с меньшей симметрией:

Симметрия	[[3,2,3]], order 72	[3,2], order 12
Диаграмма Коксетера
Диаграмма Шлегеля
Название	t2α5^[англ.]	t03α5^[англ.]	t03γ5^[англ.]	t03β5^[англ.]

Биспрямлённые 16-ячеечные соты^[англ.] также имеют 3-3 дуопризму в качестве вершинных фигур. Имеется три построения для сот с двумя меньшими симметриями.

Симметрия	[3,2,3], порядок 36	[3,2], порядок 12	[3], порядок 6
Диаграмма Коксетера
Косая ортогональная проекция

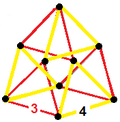
Связанные комплексные многоугольники

Правильный комплексный многогранник ₃{4}₂, в ${\displaystyle \mathbb {C} ^{2}}$ имеет вещественное представление как 3-3 дуопризма в 4-мерном пространстве. ₃{4}₂ имеет 9 вершин и 6 3-рёбер. Его группа симметрии ₃[4]₂ имеет порядок 18. Многогранник имеет также построение с меньшей симметрией или ₃{}×₃{} с симметрией ₃[2]₃ порядка 9. Эта симметрия возникает, если красные и синие 3-рёбра считать различными^[1].

Перспективная проекция

Ортогональная проекция с совпадающими центральными вершинами

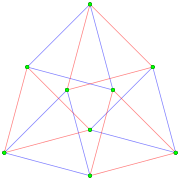
Ортогональная проекция со смещением, чтобы избежать наложение элементов.

Связанные многогранники

k₂₂ фигуры в n-мерных пространствах

Пространство	Конечное			Евклидово	Гиперболическое
n	4	5	6	7	8
Группа Коксетера	2A2	A5	E6	${\displaystyle {\tilde {E}}_{6}}$=E6^+	${\displaystyle {\bar {T}}_{7}}$=E6^++
Диаграмма Коксетера
Симметрия	[[3^2,2,-1]]	[[3^2,2,0]]	[[3^2,2,1]]	[[3^2,2,2]]	[[3^2,2,3]]
Порядок	72	1440	103,680	∞
Граф				∞	∞
Название	-122	022	122	222	322

3-3 дуопирамида

3-3 дуопирамида
Type	Однородная двойственная дуопирамида^[англ.]
Символ Шлефли	{3}+{3} = 2{3}
Диаграмма Коксетера
Ячейки	9 равногранных тетраэдров
Грпани	18 равнобедренных треугольников
Рёбер	15 (9+6)
Вершин	6 (3+3)
Симметрия^[англ.]	[[3,2,3]] = [6,2^+,6], order 72
Двойственный	3-3 дуопризма
Свойствия	выпуклый, вершинно однородный, гранетранзитивный

Двойственный многогранник для 3-3 дуопризмы называется 3-3 дуопирамидой^[англ.] или треугольной дуопирамидой. Он имеет 9 ячеек в виде равногранных тетраэдров, 18 треугольных граней, 15 рёбер и 6 вершин.

Многогранник можно рассматривать в ортогональной проекции как 6-угольник, в котором рёбра соединяют все пары вершин, точно как в 5-симплексе.

ортогональная проекция

Связанный комплексный многоугольник

Комплексный многоугольник ₂{4}₃ имеет 6 вершин в ${\displaystyle \mathbb {C} ^{2}}$ с вещественным представлением в ${\displaystyle \mathbb {R} ^{4}}$ с тем же расположением вершин^[англ.] как у 3-3 дуопирамиды. Многогранник имеет 9 2-рёбер, соответствующих рёбрам 3-3 дуопирамиды, но 6 рёбер, соединяющих два треугольника, не включены. Его можно рассматривать в шестиугольной проекции с 3 наборами раскрашенных рёбер. Это расположение вершин и рёбер даёт полный двудольный граф, в котором каждая вершина одного треугольника связана с каждой вершиной другого. Граф называется также графом Томсена или 4-клеткой^[2].

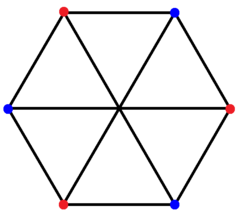
2{4}3 с 6 вершинами (синими и красными) связанные 9 2-рёбрами в виде полного двудольного графа.

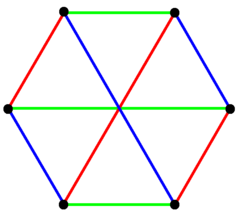
Граф имеет 3 набора из 3 рёбер, показанных цветом.

См. также

• 3,4-дуопризма
• Тессеракт (4-4 дуопризма)
• 5,5-дуопризма
• Выпуклые правильные 4-мерные многогранники
• Дуоцилиндр^[англ.]

Примечания

1. Coxeter, 1991.
2. Coxeter, 1991, с. 110, 114.

Литература

• Coxeter H.S.M. Regular Polytopes^[англ.]. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
• Coxeter H.S.M. Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — С. 212-213. — ISBN 0-486-40919-8.
  • Coxeter H.S.M. Regular Skew Polyhedra in Three and Four Dimensions // Proc. London Math. Soc.. — 1937. — Вып. 43. — С. 33–62.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 26 // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
• N.W. Johnson. Uniform Polytopes. — 1991. — (Manuscript).
  • N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
• Catalogue of Convex Polychora, section 6 George Olshevsky
• Glossary for Hyperspace (Словарь терминов) George Olshevsky
• Apollonian Ball Packings and Stacked Polytopes // Discrete & Computational Geometry. — 2016. — Июнь (т. 55, вып. 4). — С. 801–826.
  • H.S.M. Coxeter. Regular Complex Polytopes. — 2nd. — Cambridge University Press, 1991. — ISBN 978-0-521-39490-1.

Ссылки

• The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
• Polygloss – glossary of higher-dimensional terms
• Exploring Hyperspace with the Geometric Product