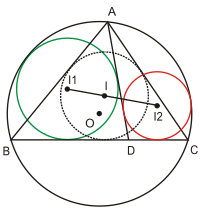
Центр вписанной окружности
| |||||||||||||||||||||||
Read other articles:

この項目では、行政官庁について説明しています。その庁舎については「福島県庁舎」をご覧ください。 福島県の行政機関福島県庁ふくしまけんちょうFukushima Prefectural Government 福島県庁舎。左側が本庁舎で、右側が西庁舎。(2009年2月19日)役職知事 内堀雅雄副知事 佐藤宏隆、鈴木正晃組織知事部局 総務部危機管理部企画調整部生活環境部保健福祉部商工労働部農林水...

College in Mount Berry, Georgia This article is about the liberal arts college in Rome, Georgia. For the private Catholic university in Miami, Florida, see Barry University. This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2022) Berry CollegeFormer namesBoys Industrial School(1902–1926)Martha Berry School for Girls (1909–1926)MottoNot to...

Nine Bostonians who organized demonstrations against the Stamp Act of 1765 Bostonians Reading the Stamp Act. From Stranger's Illustrated Guide to Boston and Its Suburbs by J. H. Stark, 1882. The Loyal Nine (also spelled Loyall Nine) were nine American patriots from Boston who met in secret to plan protests against the Stamp Act of 1765. Mostly middle-class businessmen, the Loyal Nine enlisted Ebenezer Mackintosh to rally large crowds of commoners to their cause and provided the protesters wit...

Dendrobium cumulatum Klasifikasi ilmiah Kerajaan: Plantae Divisi: Tracheophyta Kelas: Liliopsida Ordo: Asparagales Famili: Orchidaceae Genus: Dendrobium Spesies: Dendrobium cumulatum Nama binomial Dendrobium cumulatumLindl. Dendrobium cumulatum adalah spesies tumbuhan yang tergolong ke dalam famili Orchidaceae. Spesies ini juga merupakan bagian dari ordo Asparagales. Spesies Dendrobium cumulatum sendiri merupakan bagian dari genus Dendrobium.[1] Nama ilmiah dari spesies ini pertama ka...

الشركة الحافظية تقسيم إداري البلد المغرب الجهة بني ملال خنيفرة الإقليم بني ملال الدائرة بني ملال الجماعة القروية سيدي جابر المشيخة سيدي جابر السكان التعداد السكاني 133 نسمة (إحصاء 2004) • عدد الأسر 25 معلومات أخرى التوقيت ت ع م±00:00 (توقيت قياسي)[1]، وت ع م+01:00 (توقيت...

Theme park in Guangdong Province, China Lionsgate Entertainment WorldLocationHengqin, Zhuhai, Guangdong, ChinaStatusOperatingOpened31 July 2019; 4 years ago (2019-07-31)[1]OwnerLionsgateThemeLionsgate charactersWebsiteOfficial website Lionsgate Entertainment World, officially abbreviated to LEW, is a theme park found on Hengqin Island, Guangdong Province, China.[2] The park opened on July 31, 2019 as the first Lionsgate Theme Park. Designed by the Thinkwell G...

Railway station in West Bengal, India Jalpaiguri Roadজলপাইগুড়ি রোড Indian Railways junction stationPlatforms on each end of tracksGeneral informationLocationRailway Road, Patkata Colony, Danguajhar, Jalpaiguri, West BengalIndiaCoordinates26°33′34″N 88°42′35″E / 26.5594°N 88.7097°E / 26.5594; 88.7097Elevation84 metres (276 ft)Owned byIndian RailwaysOperated byNortheast Frontier RailwayLine(s)Barauni–Guwahati line, New Mal–...

Mineral from the class of hydrous sulfates PicromeritePicromerite on haliteGeneralCategorySulfate mineralFormula(repeating unit)K2Mg(SO4)2·6H2OIMA symbolPmr[1]Strunz classification7.CC.60Dana classification29.03.06.01Crystal systemMonoclinicCrystal classPrismatic (2/m) (same H-M symbol)Space groupP21/aUnit cella = 9.07, b = 12.21, c = 6.11 [Å]; β = 104,8°; Z = 2IdentificationColorColorless; white, grey, reddish, yellowishCrystal habitmassive aggregates; crusts; pris...

Major Arcana Tarot card Justice (XI) from the Rider–Waite tarot deck Justice is a Major Arcana tarot card, numbered either VIII or XI, depending on the deck. This card is used in game playing as well as in divination. Description The Justice card, as a member of the tarot deck, appears in early tarot, such as the Tarot de Marseilles. It is part of the tarot's Major Arcana, and usually follows the Chariot, as card VIII, although some decks vary from this pattern. The virtue Justice accompani...

Paulus ist eine Weiterleitung auf diesen Artikel. Weitere Bedeutungen sind unter Paulus (Begriffsklärung) aufgeführt. Paulus von Tarsus (griechisch Παῦλος Paûlos, hebräischer Name שָׁאוּל Scha’ul [Saul, umgangssprachlich (bzw. latinisiert) Saulus], lateinisch Paulus; * vermutlich vor dem Jahr 10 in Tarsus/Kilikien; † nach 60, vermutlich in Rom) war nach dem Neuen Testament (NT) der bedeutendste Missionar des Urchristentums und einer der ersten christlichen Theologen. Da ...

Skyscraper in Manila, Philippines Philippine Stock Exchange TowerThe PSE Tower in Bonifacio Global CityGeneral informationStatusCompletedTypeOfficeLocationOne Bonifacio High Street, 5th Avenue cor. 28th Street, Bonifacio Global City, Taguig, Metro Manila, PhilippinesConstruction started2012Completed2017Cost₱ 3.5 BillionOwnerPhilippine Stock ExchangeHeightRoof114.41 m (375.36 ft)[1]Technical detailsFloor count30Floor area41,389 m2 (445,507.49 sq ft)Lifts/elev...

2001 video gameProject EdenCover artDeveloper(s)Core DesignPublisher(s)Eidos InteractiveDesigner(s)Heather GibsonNeal BoydProgrammer(s)Gavin RummeryArtist(s)Stuart AtkinsonJoss CharmetPlatform(s)Microsoft Windows, PlayStation 2ReleaseWindowsNA: 12 October 2001[1][2]EU: 26 October 2001PlayStation 2NA: 22 October 2001EU: 2 November 2001Genre(s)Action-adventureMode(s)Single-player, multiplayer Project Eden is a 2001 action-adventure video game developed by Core Design and publish...

Wang ManyuWang Manyu, 2017Personal informationNama asli王曼昱[1]Kebangsaan TiongkokLahir9 Februari 1999 (umur 24)Qiqihar, Heilongjiang, ChinaGaya bermainRight-handed, shakehand grip[1]Peringkat tertinggi2 (Mei 2023)Peringkat sekarang2 (Mei 2023)[2]KlubChangbai Mountain RCB[3] Rekam medali Putri tenis meja Mewakili Tiongkok Turnamen 1 2 3 Olympic Games 1 0 0 World Championships 4 0 1 Total 5 0 1 Olimpiade 2020 Tokyo Team Kejuaraan Dunia 2021 H...

Methods and instruments used to observe the Moon The waxing gibbous Moon as viewed from Earth The Moon is the largest natural satellite of and the closest major astronomical object to Earth. The Moon may be observed by using a variety of optical instruments, ranging from the naked eye to large telescopes. The Moon is the only celestial body upon which surface features can be discerned with the unaided eyes of most people. Optimal viewing times Shadows provide a sense of depth. Contrary to pop...

The name of this television news uses a disambiguation style that does not follow WP:NCTV or WP:NCBC and needs attention. If you are removing this template without fixing the naming style to one supported by WP:NCTV, please add the article to Category:Television articles with disputed naming style. Irish TV series or programme One to OneGenreInterviewPresented byRichard Crowley Paul Cunningham Bryan Dobson Aine Lawlor George Lee Cathal Mac Coille John MurrayCountry of originIrelandOrigin...

The Right ReverendIgnatius ConradOSBAbbotNative nameNicholas ConradElectedMarch 24, 1892OrdersOrdinationSeptember 17, 1871by Bishop Kaspar WilliRankAbbotPersonal detailsBorn(1846-11-13)November 13, 1846Au, SwitzerlandDiedMarch 13, 1926(1926-03-13) (aged 79)Baldegg, SwitzerlandBuriedEinsiedeln AbbeyNationalitySwissDenominationRoman CatholicParentsJohann Conrad and Gertrude KűngOccupationAbbotProfessionBenedictine monk Ignatius Conrad OSB (November 13, 1846 Au, Switzerland – March ...

Gorilla IvanIvan in 2009SpeciesWestern lowland gorillaSexMaleBorn1962Democratic Republic of CongoDiedAugust 21, 2012(2012-08-21) (aged 49–50)Atlanta, Georgia, U.S.https://ivanthegorilla.org Ivan was a western lowland gorilla born in 1962 in what is now the Democratic Republic of the Congo. He was captured from the wild as a baby and brought to live with humans. For the first few years of his life he lived with his owners, but he soon grew too big for a human house and they moved him to...

Manual of Style This page falls within the scope of the WikiProject Manual of Style, an initiative aimed at identifying and rectifying contradictions and redundancies, improving language usage, and harmonizing the pages that constitute the MoS guidelines.Manual of StyleWikipedia:WikiProject Manual of StyleTemplate:WikiProject Manual of StyleManual of Style articlesThe contentious topics procedure is applicable to this page. It is closely associated with the English Wikipedia Manual of Style a...

АО «Казахский научно-исследовательский институт энергетики имени академика Ш. Ч. Чокина»(АО «КазНИИ энергетики им. академика Ш. Ч. Чокина») Прежнее название Казахский научно-исследовательский институт энергетики Академии наук Казахской ССР Основан 1944 Директор Абдуллае...

English footballer Poppy Pattinson Pattinson with Brighton in 2023Personal informationFull name Poppy Olivia PattinsonDate of birth (2000-04-30) 30 April 2000 (age 23)Place of birth Houghton-le-Spring, EnglandHeight 1.67 m (5 ft 6 in)Position(s) Left-backTeam informationCurrent team Brighton & Hove AlbionNumber 3Youth career2008–2013 Sunderland2013–2015 MiddlesbroughSenior career*Years Team Apps (Gls)2015–2017 Sunderland 4 (0)2017–2018 Manchester City 0 (0)2018...