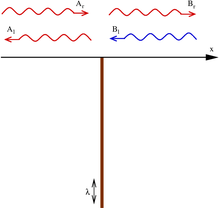
Дельтообразный потенциал в квантовой механике
|
Read other articles:

American tennis player Evelyn SearsEvelyn Sears, from a 1908 publicationFull nameEvelyn Georgianna SearsCountry (sports) United StatesBorn(1875-03-09)March 9, 1875Waltham, MA, United StatesDiedNovember 10, 1966(1966-11-10) (aged 91)Waltham, MA, United StatesSinglesGrand Slam singles resultsUS OpenW (1907)DoublesGrand Slam doubles resultsUS OpenW (1908) Evelyn Georgianna Sears (March 9, 1875 – November 10, 1966) was an American tennis player at the beginning of the 20th c...
Список Народных артистов РСФСР Ниже приведён список Народных артистов РСФСР по годам присвоения звания. Это служебный список статей, созданный для координации работ по развитию темы. Его необходимо преобразовать в информационный список или глоссарий, в противном сл�...

2019 King's Cup Sepaktakraw World ChampionshipFashion Island Shopping Mall, the venue of the tournamentTournament detailsHost country ThailandCityBangkokDates25 August –1 September 2019Teams36 countries (from International Sepaktakraw confederations)Venue(s)Fashion IslandFinal positionsChampions MD–PM: Myanmar MD–D1: Singapore MR–PM: Thailand MR–D1: India MT–PM: Thailand MT–D1: Iran MH–PM: Thailand WD–PM: Myanmar WR–PM: Thailand WT–PM: Thailand WH–PM: Thailan...

لمعانٍ أخرى، طالع الرابح الأكبر (توضيح). يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) الرابح الأكبر (الموسم الأول) النوع تلفزيون الواقع السلسلة ا

كريم الحسيني معلومات شخصية اسم الولادة كريم أحمد الحسيني الميلاد 9 فبراير 1984 (العمر 39 سنة)القاهرة، مصر الجنسية مصر الحياة العملية المدرسة الأم المعهد العالي للفنون المسرحية المهنة ممثل، ومؤدي أصوات، وكاتب اللغات العربية سنوات النشاط 1995 - حتي الان المواقع ال

В Википедии есть статьи о других людях с такой фамилией, см. Белкин; Белкин, Михаил.В статье не хватает ссылок на источники (см. рекомендации по поиску). Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авт�...

For broader coverage of this topic, see Radio regulation. This article's use of external links may not follow Wikipedia's policies or guidelines. Please improve this article by removing excessive or inappropriate external links, and converting useful links where appropriate into footnote references. (September 2020) (Learn how and when to remove this template message) Basic data Short title: ITU Radio Regulations Long title: Radio Regulations of the International Telecommunication Union Type:...

U-23サッカー大韓民国代表 国または地域 韓国協会 大韓サッカー協会FIFAコード KOR愛称 アジアの虎、太極戦士監督 黄善洪最多出場選手 李基珩(朝鮮語版)(48試合)最多得点選手 崔龍洙(25得点) ホームカラー アウェイカラー オリンピック出場回数 8回最高成績 3位 (2012)AFC U23アジアカップ出場回数 5回最高成績 優勝 (2020)表示 U-23サッカー大韓民国代表(U-23サッカーだ�...

Israeli politician and historian Ben-Zion DinurMinisterial roles1951–1955Minister of EducationFaction represented in the Knesset1949–1951Mapai Personal detailsBorn(1884-01-02)2 January 1884Khorol, Russian EmpireDied8 July 1973(1973-07-08) (aged 89) Ben-Zion Dinur (Hebrew: בן ציון דינור) (January 1884 – 8 July 1973) was a Zionist activist, educator, historian and Israeli politician. Biography Ben-Zion Dinur (far left, middle row) with Hebrew writers in Odessa, 1921 Be...

Underground lair where ants live, eat, and tend eggs Anthill redirects here. For the novel, see Anthill: A Novel. Walter R. Tschinkel next to a plaster cast of a Pogonomyrmex badius nest Ant hill and ant tracks, Oxley Wild Rivers National Park, New South Wales An ant colony is a population of a single ant species able to maintain its complete lifecycle. Ant colonies are eusocial, communal, and efficiently organized and are very much like those found in other social Hymenoptera, though the var...

2011 film by Steve James The InterruptersTheatrical posterDirected bySteve JamesProduced bySteve JamesAlex KotlowitzZak Piper (co-producer)StarringRicardo Cobe WilliamsEddie BocanegraAmeena MatthewsTio HardimanGary SlutkinCinematographySteve JamesEdited bySteve JamesAaron WickendenMusic byJoshua AbramsProductioncompanyKartemquin Films / Rise FilmsDistributed byCinema Guild (US Theatrical), PBSd (US DVD), Dogwoof (UK)Release date January 22, 2011 (2011-01-22) (Sundance) Runn...

Il capo della Rappresentanza Permanente d'Italia presso Nazioni Unite è il capo della missione diplomatica della Repubblica Italiana presso l'Organizzazione delle Nazioni Unite in New York. L'incarico ha inizio il 14 dicembre 1955, giorno dell'ingresso dell'Italia nell'organizzazione (dal 1952 era membro osservatore)[1]. Di norma viene incaricato un diplomatico italiano con il grado di ambasciatore e si occupa di tutti i programmi, i fondi, gli uffici e le commissioni in cui la nazio...

Teluk Meksiko dengan 3D Cantarell Teluk Meksiko (bahasa Inggris: Gulf of Mexico; Spanyol: Golfo de México) adalah bagian dari Laut Karibia yang dibatasi oleh Meksiko di sebelah barat dan selatan serta Amerika Serikat di sebelah utara dan barat. New Orleans dan Houston merupakan kota pelabuhan utama di teluk ini. Di Amerika Serikat, negara bagian yang melintasi teluk ini adalah Florida, Alabama, Mississippi, Louisiana, dan Texas serta di Meksiko, negara bagian yang melintasi teluk ini...

Role of Scotland during the Wars of the Three Kingdoms (1639–1653) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Scotland in the Wars of the Three Kingdoms – news · newspapers · books · scholar · JSTOR (June 2022) (Learn how and when to remove this template message) This article includes a list of refere...

Ini adalah nama Mandailing, marganya adalah Nasution. H.Yunan NasutionAnggota Dewan Perwakilan Rakyat SementaraMasa jabatan1950–1956PresidenSoekarno Informasi pribadiLahir(1913-11-22)22 November 1913Botung, Kotanopan, Mandailing Natal, Karesidenan Tapanuli, Sumatera Utara, Hindia BelandaMeninggal29 November 1996(1996-11-29) (umur 83)Rumah Sakit Islam Jakarta[1]KebangsaanIndonesiaPartai politikMasyumiSuami/istriNadimah TandjungSunting kotak info • L • B H. Mohammad...

ДепартаментЛуарефр. Loiret Флаг Герб 47°55′00″ с. ш. 02°10′00″ в. д.HGЯO Страна Франция Входит в Центр — Долина Луары Включает 3 округов, 41 кантонов и 334 коммун Адм. центр Орлеан Председатель генерального совета Эрик Долиже История и география Дата образования 4 мар...

Cosmos Niagwan je Alagba ni Ile Alagba Asofin Naijiria lati 2003 de 2007. Àyọkà yìí tàbí apá rẹ̀ únfẹ́ àtúnṣe sí. Ẹ le fẹ̀ jù báyìí lọ tàbí kí ẹ ṣàtúnṣe rẹ̀ lọ́nà tí yíò mu kúnrẹ́rẹ́. Ẹ ran Wikipedia lọ́wọ́ láti fẹ̀ẹ́ jù báyìí lọ. Itokasi wọaÀwọn ọmọ ẹgbẹ́ Ilé Alàgbà Aṣòfin ilẹ̀ Nàìjíríà ni Ilé-ìgbìmọ̀ Aṣòfin 5k (2003-2007) AbiaN Uche Chukwumerije (PDP)C Chris Adighije (PDP)S ...

معركة آق تشاي رسم تخيلي للسلطان بايزيد الأول المنتصر في معركة آق تشاي معلومات عامة التاريخ 1397م-1398م النتيجة ناصر حاسم للعثمانيين المتحاربون الدولة العثمانية إمارة قرمان القادة السلطان بايزيد الأول علاء الدين علي بك القرماني تعديل مصدري - تعديل معركة أق تشاي (بالتركية: ...

Para otros usos de este término, véase Shrewsbury (desambiguación). Shrewsbury Ciudad Centro de la localidad con el edificio del antiguo mercado en primer plano BanderaEscudo Lema: Floreat Salopia ShrewsburyLocalización de Shrewsbury en Inglaterra ShrewsburyLocalización de Shrewsbury en ShropshireCoordenadas 52°42′29″N 2°45′16″O / 52.708055555556, -2.7544444444444Idioma oficial inglésEntidad Ciudad • País Reino Unido Reino UnidoEventos históricos...
Paghimo ni bot Lsjbot. Alang sa ubang mga dapit sa mao gihapon nga ngalan, tan-awa ang Rush Spring. 37°31′14″N 108°29′04″W / 37.52052°N 108.48431°W / 37.52052; -108.48431 Rush Spring Tubud Nasod Tinipong Bansa Estado Colorado Kondado Montezuma County Gitas-on 2,212 m (7,257 ft) Tiganos 37°31′14″N 108°29′04″W / 37.52052°N 108.48431°W / 37.52052; -108.48431 Timezone MST (UTC-7) - summer (DST) MDT (U...







![{\displaystyle {\hat {H}}\psi (x)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}+U(x)\right]\psi (x)=E\psi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/754e843d6c01fee47d437686320cdbda0bd4c87f)