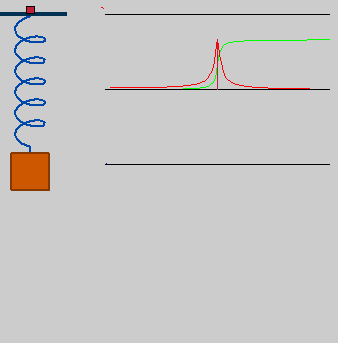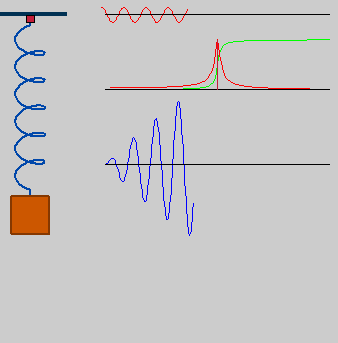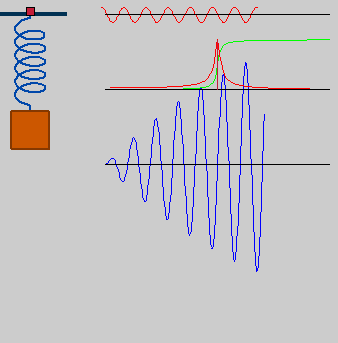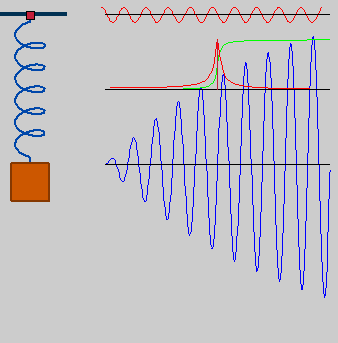
Ressonância
|
Read other articles:

Untuk tulisan lainnya yang dikaitkan dengan Henokh, lihat Kitab Henokh (disambiguasi). Bagian dari Alkitab KristenPerjanjian LamaYosua 1:1 pada Kodeks Aleppo Taurat Kejadian Keluaran Imamat Bilangan Ulangan Sejarah Yosua Hakim-hakim Rut 1 Samuel 2 Samuel 1 Raja-raja 2 Raja-raja 1 Tawarikh 2 Tawarikh Ezra Nehemia Ester Puisi Ayub Mazmur Amsal Pengkhotbah Kidung Agung Kenabian Besar Yesaya Yeremia Ratapan Yehezkiel Daniel Kecil Hosea Yoël Amos Obaja Yunus Mikha Nahum Habakuk Zefanya Hagai Zakh...

2023 Peruvian filmThe Last LaughTheatrical release posterDirected byGonzalo LadinesWritten byGonzalo LadinesProduced byEnid CamposGonzalo LadinesGonzalo CarracedoKarina JuryStarringCésar RitterGisela Ponce de LeónCinematographyFernando CobianEdited byChino PintoMusic byRuiz-GonzalezProductioncompanies17 ProduccionesFunny Games FilmsTodo lo DemásRelease datesAugust 11, 2023 (Lima)January 4, 2024 (Peru)Running time90 minutesCountryPeruLanguageSpanish The Last Laugh (Spanish: Muerto de risa, ...

Para otros usos de este término, véase Acta de Unión. Islandia en 1910, mapa elaborado por el geógrafo Þorvaldur Thoroddsen. El Acta de Unión entre Dinamarca e Islandia es un acuerdo firmado por Islandia y Dinamarca el 1 de diciembre de 1918. Contenido El Acta mediante el cual se reconoce a Islandia como un Estado completamente soberano, el Reino de Islandia, vinculado a Dinamarca mediante una unión personal con el rey de Dinamarca. Islandia creó su propia bandera, declaró su neutral...

National dish of Laos For the literary magazine, see Los Angeles Review of Books. Laab / LarbLarb made with cooked beef in Vientiane, LaosAlternative namesLap, Larp, Lahp, Lahb, LaabTypeSaladPlace of originLaosCreated byLaoMain ingredientsMeat (chicken, beef, duck, turkey, pork, or fish)VariationsSeveral across the world Media: Laab / Larb A Lao-style larb ped (with duck) in Chiang Mai Larb khua mu, a stir-fried northern Thai larb made with pork, in Chiang Mai Laab / Larb (Lao: ລາ

بيف ماجواير (بالإنجليزية: Biff McGuire) معلومات شخصية اسم الولادة (بالإنجليزية: William McGuire) الميلاد 25 أكتوبر 1926[1] نيو هيفن، كونيتيكت تاريخ الوفاة 9 مارس 2021 (94 سنة) [2] مواطنة الولايات المتحدة الزوجة جيني كارسون (1960–2021) عدد الأولاد 2 الحياة العملية...

Трипільська культура(4800 - 3000 рр. до н.е.)Характерний зразок кераміки культури Трипілля-Кукутень Розділи Поселення Архітектура Горизонт згорілих будинків Релігія Господарство Занепад Пов'язані статті Неоліт Європи Енеоліт «Стара Європа» ← Боянська культура Ямна куль�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2015) تيتي روبن معلومات شخصية اسم الولادة تيتي روبن الميلاد 26 أغسطس 1957 (العمر 66 سنة) فرنسا الجنسية فرنسا الحياة الفنية النوع موسيقى العالم الآلات الموسيقية ع

Con lắc của Foucault ở Panthéon của Paris có thể đo thời gian cũng như chứng minh sự quay của Trái đất. Thời gian trong vật lý được định nghĩa bởi phép đo của chính nó: thời gian là những gì được đọc trên đồng hồ. Trong kinh điển, vật lý phi tương đối, nó là một đại lượng vô hướng, giống như chiều dài, khối lượng và điện tích, thường được mô tả như một đại lượng c

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 新潟県道12号松代高柳線 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2018年6月) 主要地方道 新潟県道12号 松代高柳
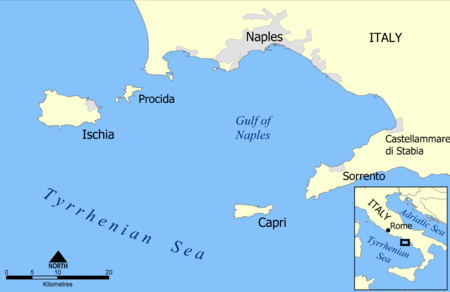
Peta Pulau Ischia Ischia merupakan sebuah pulau gunung berapi di Laut Tirrhenia, di bagian utara Teluk Napoli. Pulau ini terletak 30 km dari Napoli. Gunung tertinggi di pulau ini adalah Gunung Epomeo dengan ketinggian 788 meter. Komunitas utama di pulau ini ialah Ischia Porto. Komunitas lainnya ialah Barano d'Ischia, Casamicciola Terme, Forio, Lacco Ameno dan Serrara Fontana. Penduduknya berjumlah lebih dari 60.335 jiwa (2007) dengan memiliki luas wilayah 46,3 km². Kepadatan pendud...

Diretoria Geral de Segurança Externa Direction générale de la Sécurité extérieure Logotipo da DGSE Sede da DGSE, em Paris. Organização Natureza jurídica Agência de segurança e Serviço de inteligência Dependência República Francesa Chefia Bernard Émié, Diretor Geral de Segurança Externa Número de funcionários 7.000 (2019), incluindo 1.000 militares7.100 (2022) Orçamento anual 880 milhões de euros (2021) Localização Sede Paris48° 52' 28 N 2° 24' 26 E Hist

Жан-П'єр Крістенфр. Jean-Pierre ChristinІм'я при народженні фр. Jean Pierre Christin[1]Народився 31 травня 1683(1683-05-31)Ліон, Ліонне, Королівство Франція[1]Помер 19 січня 1755(1755-01-19) (71 рік)Ліон, Ліонне, Королівство Франція[1]Країна ФранціяНаціональність французДіяльність астроном, м...

Kathedrale in Wells Das Bistum Bath und Wells (lat.: Dioecesis Bathoniensis et Wellensis) ist eine anglikanische Diözese in der Kirchenprovinz Canterbury der Church of England mit Sitz in Wells. Bis zur englischen Reformation war es eine römisch-katholische Diözese. Inhaltsverzeichnis 1 Geschichte 2 Siehe auch 3 Literatur 4 Weblinks Geschichte Abteikirche Bath, ehemals Kathedrale Das Bistum Bath und Wells wurde im Jahre 909 aus Gebietsabtretungen des Bistums Sherborne als Bistum Wells erri...

Nazi concentration camp in Serbia SajmišteConcentration campThe central tower of the Sajmište fairgrounds, 2010.Location of Sajmište within occupied YugoslaviaCoordinates44°48′46″N 20°26′42″E / 44.81278°N 20.44500°E / 44.81278; 20.44500LocationStaro Sajmište, Independent State of CroatiaOperated by Nazi Germany (September 1941 – May 1944) Independent State of Croatia (May–July 1944) Original useExhibition centreOperationalSeptember ...

German World War II fighter pilot For other people named Otto Schulz, see Otto Schulz (disambiguation). Otto SchulzOtto Schulz in World War IINickname(s)Eins-Zwei-Drei SchulzBorn(1911-02-11)11 February 1911Treptow an der Rega, Kingdom of Prussia, German EmpireDied17 June 1942(1942-06-17) (aged 31)near Sidi Rezegh, Italian LibyaAllegiance Nazi GermanyService/branch LuftwaffeYears of service1934–1942RankOberleutnant (first lieutenant)UnitJagdgeschwader 27Battles/warsSee ba...

Dutch futurologist This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Fred Polak – news · newspapers · books · scholar · JSTOR (September 2020) Fred Polak (1970) Frederik Lodewijk Polak (21 May 1907, in Amsterdam – 17 September 1985, in Wassenaar) was one of the Dutch founding fathers of futures stu...

17th-century colonies of Sweden in the Americas This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Swedish colonies in the Americas – news · newspapers · books · scholar · JSTOR (March 2014) (Learn how and when to remove this template message) Part of a series onEuropean colonizationof the Americas First wave B...

1962 studio album by Sonny StittFeelin'sStudio album by Sonny StittReleased1962RecordedFebruary–April 1962 New York CityGenreJazzLabelRoostRLP 2247ProducerTeddy ReigSonny Stitt chronology Soul Summit(1962) Feelin's(1962) Low Flame(1962) Professional ratingsReview scoresSourceRatingDown Beat[1]Allmusic[2] Feelin's is an album by saxophonist Sonny Stitt recorded in 1962 and originally released on the Roost label.[3] Reception The Allmusic site awarded the album...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 10 de septiembre de 2015. Puntos de Breves Microrregión MapaCoordenadas 1°40′55″S 50°28′48″O / -1.681944, -50.48Entidad Microrregión • País Brasil • Estado Pará • Mesorregión MarajóSuperficie • Total 30.094,393 km²Población (est. 2006) • Total 187,176 hab. • Densidad 6,2 ha...

This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (September 2023) (Learn how and when to remove this template message) WestcottIndustrySchool and Office productsOwnerAcme United CorporationWebsitehttps://www.westcottbrand.com/ The history of school and office products brand Westcott dates back to 1872, when Henry ...