P-completo
|
Read other articles:
Provinsi Ravenna Negara Italia Wilayah / Region Emilia-Romagna Ibu kota Ravenna Area 1,858 km2 Population (2008) 383,945 Kepadatan 206.6 inhab./km2 Comuni 18 Nomor kendaraan RA Kode pos 48010-48015, 48017, 48018, 48020, 48022, 48024-48027, 48100 Kode area telepon 0544, 0545, 0546 ISTAT 039 Presiden Francesco Giangrandi Executive Democratic Party Peta yang menunjukan lokasi provinsi Ravenna di Italia Provinsi Ravenna merupakan sebuah provinsi di Italia. Provinsi ini memiliki luas wilayah...

One of the five Nobel Prizes established in 1895 by Alfred Nobel For a list of laureates, see List of Nobel laureates in Physics. AwardNobel Prize in PhysicsAwarded forOutstanding contributions for humankind in the field of physicsLocationStockholm, SwedenPresented byRoyal Swedish Academy of SciencesReward(s)11 million Swedish kronor (2023)[1]First awarded1901Last awarded2023Most recently awarded toPierre Agostini, Ferenc Krausz, and Anne L'HuillierMost awardsJohn Bardeen (2)Websiteno...

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. Donkey Kong Country 2: Diddy's Kong Quest InformationOriginaltitelスーパードンキーコング 2UtvecklareRareUtgivareNintendoGenrePlattformsspelAntal spelare1-2FormatSuper NES, Game Boy Advance, WiiArbetslagReg...
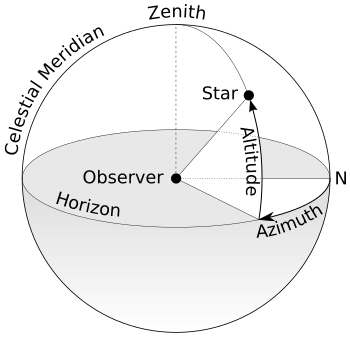
Hệ tọa độ chân trời sử dụng một thiên cầu lấy tâm là người quan sát. Góc phương vị được đo từ điểm bắc (nhưng đôi khi từ điểm nam) và thuận theo hướng đông ở trên đường chân trời; góc cao là góc thẳng đứng so với đường chân trời Hệ tọa độ chân trời là một hệ tọa độ thiên thể sử dụng mặt phẳng chân trời địa phương của người quan sát làm mặt phẳng cơ bản (m...

Pour les articles homonymes, voir Dauphin (homonymie). Cet article est une ébauche concernant un peintre français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. François-Gustave DauphinBiographieNaissance 7 juin 1804BelfortDécès 23 mai 1859 (à 54 ans)Ancien 2e arrondissement de ParisSépulture Cimetière de MontmartreNationalité françaiseFormation École nationale supérieure des beaux-arts (à par...

Pour les articles homonymes, voir Chardon (homonymie). Ordre du Chardon Insigne de l'ordre du Chardon Décernée par Écosse Type Ordre de chevalerie Décerné pour À la volonté du monarque aux chevaliers écossais Statut Toujours décerné Chiffres Date de création 1687 Importance Ordre de Saint-Patrick ()Ordre du Bain () Ordre de la Jarretière Ruban de l'ordre modifier Chevalier de l’ordre du Chardon.Le prince Augustus Frederick, duc du Sussex, en tenue de chevalier (1842). L’...

Provider of public access Wi-Fi hotspots in the United Kingdom This article is about the European public free access Wi-Fi company. For other uses, see The Cloud (disambiguation). The CloudTypeDivisionIndustryPublic access Wi-FiFoundedJanuary 2003; 20 years ago (2003-01)HeadquartersSt Albans, Hertfordshire, United KingdomNumber of locations22,000Area servedUnited KingdomKey peopleVince Russell(Managing Director)Number of employees100ParentSky UKWebsitewww.thecloud.net T...

لينزي روزينوالد معلومات شخصية تاريخ الميلاد 1955 (العمر 68 سنة) الحياة العملية المدرسة الأم جامعة ولاية بنسلفانيا المهنة عالم التقانة الحيوية [لغات أخرى] المواقع الموقع الموقع الرسمي تعديل مصدري - تعديل هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة �...

Lambang Timor Leste sejak tahun 2007 Lambang Negara Timor Leste ditetapkan pada tanggal 18 Januari 2007 berdasarkan Undang-undang No.02/2007. Rancangan lambang ini dibuat berdasarkan lambang pada saat Timor Leste mendeklarasikan kemerdekaan secara sepihak pada tanggal 28 November 1975. Di bagian tengah lambang negara Timor Leste terdapat piramida segitiga lengkung dengan pinggiran berwarna merah, kuning dan bagian tengah berwarna hitam yang melambangkan Gunung Ramelau di Timor Leste. Pada bid...

Armed conflict in the Utah Territory in 1857–1858 Utah WarPart of the Mormon warsDateMarch 1857 – July 1858LocationUtah Territory(present day Utah and Wyoming)Result Inconclusive Resolution through negotiation Brigham Young replaced as Governor of Utah Territory Full amnesty for charges of sedition and treason issued to the citizens of Utah Territory by President James Buchanan if they accepted US federal authorityBelligerents United States Deseret / Utah Native American alliesComma...

Gallic tribeThis article or section should specify the language of its non-English content, using {{lang}}, {{transliteration}} for transliterated languages, and {{IPA}} for phonetic transcriptions, with an appropriate ISO 639 code. Wikipedia's multilingual support templates may also be used. See why. (June 2021) Map of Gaul with tribes, 1st century BC; the Petrocorii are circled. The Petrocorii were a Gallic tribe dwelling in the pr...

Вижницький район адміністративно-територіальна одиниця Герб Прапор Колишній район на карті Чернівецька область Основні дані Країна: Україна Область: Чернівецька область Код КОАТУУ: 7320500000 Утворений: 5 липня 1940 р. Ліквідований: 17 липня 2020 Населення: ▼ 55 381 (на 1.1.2019) Пл...

2016 Japanese filmHentai Kamen: Abnormal CrisisPosterKanjiHK 変態仮面 アブノーマル・クライシス Directed byYūichi Fukuda [ja]Screenplay byYūichi FukudaBased onKyūkyoku!! Hentai Kamenby Keishū Ando [ja]StarringRyohei SuzukiDistributed byToei CompanyRelease date May 14, 2016 (2016-05-14) Running time118 minutes[1]CountryJapanLanguageJapanese Hentai Kamen: Abnormal Crisis (HK 変態仮面 アブノーマル・クライシス...

Protein-coding gene in the species Homo sapiens ATF3IdentifiersAliasesATF3, activating transcription factor 3External IDsOMIM: 603148 MGI: 109384 HomoloGene: 1265 GeneCards: ATF3 Gene location (Human)Chr.Chromosome 1 (human)[1]Band1q32.3Start212,565,334 bp[1]End212,620,777 bp[1]Gene location (Mouse)Chr.Chromosome 1 (mouse)[2]Band1 H6|1 96.28 cMStart190,902,493 bp[2]End190,950,236 bp[2]RNA expression patternBgeeHumanMouse (ortholog)Top expre...

A list of films produced in Russia in 2022 (see 2022 in film). Film releases Opening Title Russian title Cast and crew Details JANUARY 1 Portrait of a Stranger Портрет незнакомца Director: Sergey Osipyan Cast: Yuri Butorin, Kirill Pirogov 6 Project Gemini Звёздный разум Director: Vyacheslav Lisnevsky Cast: Egor Koreshkov, Alyona Konstantinova, Konstantin Samoukov KD Studios 6 Swingers Свингеры Director: Dmitry Fiks, Andreys Ekis Cast: Dmitry Nagiyev, Irin...

For the 1995 film, see Expect No Mercy (film). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Expect No Mercy – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) 1977 studio album by NazarethExpect No MercyStudio album by NazarethRelease...

Road in Ho Man Tin, Hong Kong King's Park Hockey Ground on Wylie Road Wylie Road (Chinese: 衛理道 or 衞理道) is a road in Ho Man Tin and King's Park, Kowloon, Hong Kong. It runs south–north from Gascoigne Road to Waterloo Road and was named after the British missionary Alexander Wylie.[1] Notable places British Military Hospital King's Park Hockey Ground [yue] Tung Wah College Parc Palais [yue] See also List of streets and roads in Kowloon Referen...

This article consists almost entirely of a plot summary. Please help improve the article by adding more real-world context. (June 2016) (Learn how and when to remove this template message) The Madagaskar Plan First editionAuthorGuy SavilleCountryUnited KingdomLanguageEnglishGenreAdventure, alternative history novelPublisherHodder & StaughtonPublication date16 July 2015Media typePrint (Hardback)Pages518 pp (first edition, hardback)ISBN978-1-444-71068-7 (first edition, hardback)Precede...

Canting arms of Rose of Wootton Fitzpaine in Dorset: Sable, on a pale or three roses gules slipt and leaved proper[1] Richard Rose (died ca. 1658) was an English merchant and politician who sat in the House of Commons from 1640 to 1648. He was the son of John Rose of Lyme Regis, Dorset and his wife Faith Ellesdon. He was a draper[2] and became Lord of the Manor of Wootton Fitzpaine.[3] In April 1640, Rose was elected Member of Parliament for Lyme Regis in the Short Par...

Book of victories, one of the best-known sources of Timur's lifeNot to be confused with Zafarnama (letter), by Guru Gobind Singh (10th Guru of the Sikhs). Timur granting audience on the occasion of his accession, from the Garrett Zafarnama The Zafarnama (Persian: ظفرنامه, lit. 'Book of Victories') is a panegyric book written by Sharaf al-Din Ali Yazdi approximately two decades after the death of its main subject, Timur, the Turco-Mongol conqueror. It was commissioned by I...
