Número semiprimo
|
Read other articles:

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ride on the Edge – news · newspapers · books · scholar · JSTOR (February 2013) (Learn how and when to remove this template message) 2007 studio album by GranrodeoRide on the EdgeStudio album by GranrodeoReleased25 July 2007GenreRockLength69:04LabelLanti...
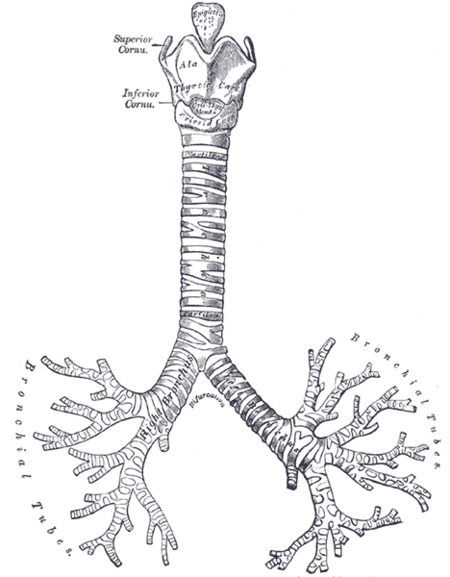
Хрящи гортани, трахеи и бронхов, спереди Главные бронхи (лат. bronchi principales) — две ветви трахеи, входящие в ворота правого и левого лёгкого. Анатомия Бифуркация трахеи, место разделения её на главные бронхи, располагается на уровне верхнего края V грудного позвонка. У же�...

Ini adalah nama Batak Angkola, marganya adalah Harahap. Burhanuddin HarahapBurhanuddin Harahap pada tahun 1956Perdana Menteri Indonesia ke-9Masa jabatan11 Agustus 1955 – 20 Maret 1956PresidenSoekarnoWakilDjanoe IsmailHarsono TjokroaminotoPendahuluAli SastroamidjojoPenggantiAli SastroamidjojoMenteri Pertahanan Indonesia ke-8Masa jabatan12 Agustus 1955 – 24 Maret 1956PresidenSoekarnoPerdana MenteriDirinya sendiriPendahuluIwa KoesoemasoemantriPenggantiAli Sastroamid...

此條目需要擴充。 (2017年1月22日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 維基百科中的法律相關內容僅供參考,並不能視作專業意見。如需獲取法律相關的幫助或意見,請諮詢所在司法管轄區的法律從業人士。詳見法律聲明。 死刑 問題 存廢問題 · 宗教與死刑(英语:Religion and capital punishment) · 冤...

Subgenus of flowering plants Iris subg. Iris Purple bearded iris Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Monocots Order: Asparagales Family: Iridaceae Subfamily: Iridoideae Tribe: Irideae Genus: Iris Subgenus: Iris subg. IrisB.Mathew Subgenus Iris is one subgenus of Iris. Iris as a plant was originally named by Carl Linnaeus in his book Systema Naturae (in 1735), with a great number of species being added into the genus. Including new ones tha...

1966 single by The Mothers of InventionWho Are the Brain Police?Single by The Mothers of Inventionfrom the album Freak Out! B-sideTrouble Every DayReleased1966 (1966)RecordedMarch 9, 1966GenreExperimental rockLength3:22LabelVerveSongwriter(s)Frank ZappaProducer(s)Frank ZappaThe Mothers of Invention singles chronology How Could I Be Such Fool? (1966) Who Are the Brain Police? (1966) Big Leg Emma (1967) Who Are the Brain Police? is a Frank Zappa song, performed by The Mothers of Invention,...

Genre of heavy metal music Gothic metalStylistic originsHeavy metalgothic rockdeath-doomCultural originsEarly 1990s, United KingdomSubgenresSymphonic gothic metalRegional scenesEnglandFinlandThe NetherlandsNorwaySwedenGermanyItalyPolandUnited StatesGreeceOther topics Alternative metal avant-garde metal list of gothic metal bands industrial metal post-metal Vibeke Stene, former female opera vocalist of influential Gothic metal band Tristania. Gothic metal (or goth metal) is a fusion genre comb...

Hospital in Dorset, EnglandAlderney HospitalGeographyLocationAlderney, Dorset, EnglandCoordinates50°45′00″N 1°56′28″W / 50.749918061270385°N 1.9412434315830047°W / 50.749918061270385; -1.9412434315830047OrganisationTypeSpecialistServicesSpecialityGeriatric care, DementiaHistoryOpened1888LinksListsHospitals in England Alderney Hospital is a hospital in Alderney, a suburb of Poole, Dorset.[1] History Alderney Hospital was built in 1888 for the care of...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Druze – news · newspapers · books · scholar · JSTOR (June 2022) (Learn how and when to remove this template message) This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with...

Author and investigative journalist Nicky HagerONZMHager in 2023BornNicolas Alfred Hager1958 (age 64–65)Levin, New ZealandOccupationInvestigative journalistNationalityNew ZealanderAlma materVictoria University of WellingtonChildren1Websitewww.nickyhager.info Nicolas Alfred Hager ONZM (born 1958) is a New Zealand investigative journalist. He has produced seven books since 1996, covering topics such as intelligence networks, environmental issues and politics. He is one of two Ne...

AfricanConservation statusFAO (2007): endangered[1]: 153 DAD-IS (2023): at risk[2]Livestock Conservancy (2023): watch[3]RBST (2023): not listed[4]Other namesAfrican GooseClassificationAPAheavy goose[5]EEyes[6]PCGBheavy[7]Anser cygnoides Brown African Goose The African or African Goose is a breed of domestic goose. It is one of two domestic breeds that derive from the wild species Anser cygnoides, the other being the Chine...

Stefan LöfvenPerdana Menteri SwediaMasa jabatan3 Oktober 2014 – 30 November 2021Penguasa monarkiCarl XVI GustafWakilMargot WallströmMorgan JohanssonÅsa RomsonIsabella Lövin Per BolundPendahuluFredrik ReinfeldtPenggantiMagdalena AnderssonPemimpin Partai Sosial DemokratMasa jabatan27 Januari 2012 – 4 November 2021PendahuluHåkan JuholtPenggantiMagdalena AnderssonPemimpin OposisiMasa jabatan27 Januari 2012 – Oktober 2014PendahuluHåkan JuholtPenggantiFredrik ...

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak men...

Television channel Astro Box OfficeCountryMalaysiaBroadcast areaBruneiMalaysiaOwnershipOwnerAstro All Asia Networks plcHistoryLaunched2000ClosedJune 1, 2021 (2021-06-01) (Tayangan Hebat)April 30, 2023 (2023-04-30) (BollyOne HD)Former namesAstro ShowcaseSeason PassLinksWebsiteAstro Malaysia Astro Box Office is a pay-per-view (PPV) system on the Astro platform in Brunei and Malaysia. It shows movies and occasionally sporting events. History Astro Box Office launche...

Jordanian campaignPart of the Six-Day WarThe Jordan salient. June 5–7Date6–7 June 1967LocationWest BankResult Israeli victoryTerritorialchanges Israel seizes the West Bank, including East JerusalemBelligerents Israel Jordan IraqCasualties and losses 550 killed, 2,400 wounded[citation needed] Jordan: 700 killed, 2,500 woundedIraq: 10 killed, 30 wounded[citation needed] vteSix-Day War Israel Waiting period Sinai Campaign Focus Abu-Ageila Um Katef El Arish Jordani...

This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (July 2022) (Learn how and when to remove this template message) Guitar amplifier Marshall JTM45 MK II Reissue Marshall JTM45 is the first guitar amplifier made by Marshall. First produced in 1963, it has been called a seminal amplifier,[1] and is praised as being among the most desirable of all the company's amplifiers.[2] His...

La recherche publique en France est la part de la recherche scientifique organisée et financée par l'État français et les collectivités territoriales françaises. Une autre part est financée par les entreprises privées, il s'agit de la recherche privée. Pour l'ensemble de sa recherche, selon les chiffres de l'OCDE, la France subit un déclassement, en 2019 son investissement à 2,9 % du PIB, la situe à la 13e place, en 1992 elle occupait la 4e place des pays de l'OCDE[1]. L’or...

Village in West Pomeranian Voivodeship, PolandBudzieńVillageBudzieńCoordinates: 53°37′N 14°41′E / 53.617°N 14.683°E / 53.617; 14.683Country PolandVoivodeshipWest PomeranianCountyGoleniówGminaStepnicaPopulation110 Budzień [ˈbud͡ʑɛɲ] is a village in the administrative district of Gmina Stepnica, within Goleniów County, West Pomeranian Voivodeship, in north-western Poland.[1] Budzień is approximately 6 kilometres (4 mi) south-east of Stepni...

Particle accelerator at CERN, Switzerland Particle accelerator Super Proton SynchrotronTest beamline delivered from the SPS. In photo 20 GeV positrons are used to calibrate the Alpha Magnetic Spectrometer.General propertiesAccelerator typeSynchrotronBeam typeprotons, heavy ionsTarget typeInjector for LHC, fixed targetBeam propertiesMaximum energy450 GeVPhysical propertiesCircumference6.9 kilometres (4.3 mi)Coordinates46°14′06″N 6°02′33″E / 46.23500°N 6.04250°E...

Film studio in Riga, Latvia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Riga Film Studio – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this template message) Riga Film Studio in 2002 Riga Film Studio (Latvian: Rīgas kinostudija, Russian: Рижская кино�...




