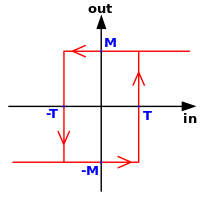
Histerese
|
Read other articles:

Mahakasih Yang IlahiGenreKidungDitulis1747TeksCharles WesleyBerdasarkan1 Yohanes 4:16Meter8.7.8.7 DMelodiBeecher karya John Zundel, Hyfrydol, Blaenwern karya William Penfro Rowlands Mahakasih Yang Ilahi atau Love Divine, All Loves Excelling adalah sebuah kidung Kristen karya Charles Wesley.[1] Secara garis besar, kidung tersebut ditemukan dalam nyaris seluruh kumpulan kidung umum pada masa lampau, tak hanya kitab-kitab kidung Methodis dan Anglikan dan kumpulan-kumpulan kidung komersia...

Halaman ini berisi artikel tentang serial manga karya Naoki Urasawa. Untuk kegunaan lain, lihat Monster (disambiguasi). Monster (manga)Gambar dari anime The MonsterGenreSeinen, Drama, Horor, Misteri, Fiksi detektif, Kejiwaan MangaPengarangNaoki UrasawaPenerbit Shogakukan AnimeSutradaraMasayuki KojimaStudioMadhouse Portal anime dan manga Bagian dari seriManga Daftar manga Simbol · A · B · C · D · E · F · ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (سبتمبر 2023) مكتب الكحول والتبغ والأسلحة النارية والمتفجرات مكتب الكحول والتبغ والأسلح

Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Julho de 2020) A Confederação Internacional de Sindicatos Livres foi criada em 1949. Possuía 236 associados espalhados em 154 países, englobando 155 milhões de pessoas. Em 2006, fundiu-se com a Confederação Mundial do Trabalho na Confederação Sindical ...

Coordenadas: 45° 37' 18 N 5° 41' 57 E Saint-Maurice-de-Rotherens Comuna francesa Localização Saint-Maurice-de-RotherensLocalização de Saint-Maurice-de-Rotherens na França Coordenadas 45° 37' 18 N 5° 41' 57 E País França Região Auvérnia-Ródano-Alpes Departamento Saboia Características geográficas Área total 8,17 km² População total (2010) [1] 217 hab. Densidade 26,6 hab./km² Código Postal 73240 ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2019) لينتون فازيل معلومات شخصية الميلاد 3 يونيو 1983 (40 سنة) لندن مواطنة المملكة المتحدة الحياة العملية المهنة فنان قتال مختلط[1] اللغات الإنجليز

Canal crossing central Scotland The Forth and Clyde Canal, near Bonnybridge and Larbert The Forth and Clyde Canal is a canal opened in 1790, crossing central Scotland; it provided a route for the seagoing vessels of the day between the Firth of Forth and the Firth of Clyde at the narrowest part of the Scottish Lowlands. This allowed navigation from Edinburgh on the east coast to the port of Glasgow on the west coast. The canal is 35 miles (56 km) long and it runs from the River Carron at...

Кіндрат Гаврилович Клименко Народження 25 жовтня 1913(1913-10-25)Шура-Копіївська (зараз Вінницька область)Смерть 10 березня 1945(1945-03-10) (31 рік)НімеччинаПоховання Західнопоморське воєводствоКраїна СРСРПриналежність Радянська арміяРід військ кавалеріяРоки служби 1934–1945...

لمعانٍ أخرى، طالع العارضة (توضيح). قرية العارضة - قرية - تقسيم إداري البلد اليمن المحافظة محافظة صنعاء المديرية مديرية بني ضبيان العزلة عزلة بني ضبيان السكان التعداد السكاني 2004 السكان 96 • الذكور 41 • الإناث 55 • عدد الأسر 9 • عدد المساكن 10 ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Universitas Dar es Salaam – berita · surat kabar · buku · cendekiawan · JSTORUniversitas Dar es SalaamUniversity of Dar es Salaam (Inggris) Chuo Kikuu cha Dar es Salaam (Swahili)MotoHekima Ni UhuruJenisP...

Sereal jagungSereal jagungTempat asalAmerika SerikatDaerahBattle Creek Sanitarium di MichiganDibuat olehJohn Harvey Kellogg (1894) W.K. KelloggBahan utamaJagung, gula, penyedap rasaVariasiberagam Cookbook: Sereal jagung Media: Sereal jagung Sereal jagung (bahasa Inggris: Corn flakes, cornflakes) adalah sebuah sereal sarapan yang dibuat dengan memanggang serpihan jagung. Sereal tersebut diciptakan oleh John Harvey Kellogg pada 1894 sebagai makanan sehat untuk para pasien Battle C...

2014 studio album by The DrumsEncyclopediaStudio album by The DrumsReleasedSeptember 23, 2014GenreIndie pop, post-punk revival, dream popLabelNorman RecordsProducerThe DrumsThe Drums chronology Portamento(2011) Encyclopedia(2014) Abysmal Thoughts(2017) Singles from Encyclopedia Magic MountainReleased: July 22, 2014[1] I Can't PretendReleased: August 26, 2014[2] Encyclopedia is the third studio album of American indie pop band The Drums. It was released on September 23,...

Hospital in Tokyo, JapanEbara HospitalHospital entranceGeographyLocationŌta, Tokyo, JapanCoordinates35°35′39″N 139°41′36″E / 35.5941°N 139.6934°E / 35.5941; 139.6934ServicesBeds506HelipadYesHistoryOpened1898LinksWebsitewww.ebara-hp.ota.tokyo.jp Ebara Hospital (荏原病院) is in Ōta, Tokyo, Japan. It has 506 beds and is run by the Tokyo Metropolitan Health and Hospitals Corporation.[1] As the hospital is located near Haneda Airport, it often prov...

For the video game character, see Venom Snake. The lateral view of a king cobra's skull showing fangs Species of the suborder Serpentes that produce venom Venomous snakes are species of the suborder Serpentes that are capable of producing venom, which they use for killing prey, for defense, and to assist with digestion of their prey. The venom is typically delivered by injection using hollow or grooved fangs, although some venomous snakes lack well-developed fangs. Common venomous snakes incl...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (June 2021) Laure Ferrari (born 6 October 1979 in Épinal, France) is the girlfriend and confidant of former MEP and UKIP leader Nigel Farage, best known for his successful Brexit campaign. Ferrari's first meeting with Farage was in 2007 when she was working in Strasbourg as a waitress.[1][2][3] Ferrari worked fo...

Untuk minuman dari Korea, lihat Sudan (minuman). Artikel ini perlu dikembangkan dari artikel terkait di Wikipedia bahasa Inggris. (Juli 2023) klik [tampil] untuk melihat petunjuk sebelum menerjemahkan. Lihat versi terjemahan mesin dari artikel bahasa Inggris. Terjemahan mesin Google adalah titik awal yang berguna untuk terjemahan, tapi penerjemah harus merevisi kesalahan yang diperlukan dan meyakinkan bahwa hasil terjemahan tersebut akurat, bukan hanya salin-tempel teks hasil terjemahan ...

Regulations imposed to prevent aircraft noise Night flying restrictions or night-time curfews,[1] including night flight bans, are any regulations or legislation imposed by a governing body to limit the ground-perceived exposure to aircraft noise pollution during the night hours, when the majority of residents are trying to sleep. Such regulations may include restrictions to available flight paths, or prohibitions against takeoffs, or prohibitions against takeoffs and landings, or pro...

Louisiana gambling casino Horseshoe Casino Hotel Bossier City Location Bossier City, Louisiana Address 711 Horseshoe BoulevardOpening date1994ThemeWesternNo. of rooms606[1]Signature attractions1931 LoungeNotable restaurantsJack Binion's Steak House 8oz Burger Bar Jasmine's Noodle BarCasino typeRiverboatOwnerVici PropertiesOperating license holderCaesars EntertainmentCoordinates32°30′56″N 93°44′13″W / 32.515438°N 93.737054°W / 32.515438; -93.737054We...

بوعلام بناني معلومات شخصية الميلاد سنة 1951 (العمر 72–73 سنة) بلدية حسين داي مواطنة الجزائر الحياة العملية المهنة ممثل اللغات العربية المواقع IMDB صفحته على IMDB تعديل مصدري - تعديل بوعلام بناني (اسمه الحقيقي بوعلام جيلالي بناني ) (مواليد عام 1940 في حسين دا�...

Cai Shen digambarkan bersama Fu Lu Shou. Dewa Kekayaan atau Cai Shen (t=財神; s=财神; pinyin=Cái Shén; WG=Tsai2 Shen2; Hokkien POJ=Tsâi-sîn; Khek=Choy Sin) atau Cai Shen Ye (Hanzi=財神爺; Hokkien=Cai Sin Ya) adalah dewa yang menguasai kekayaan, harta, atau rezeki dalam mitologi Tiongkok. Dalam bahasa Vietnam, ia disebut Thần Tài (Chữ nôm=神財). Cai Shen dipuja sebagai dewa dalam kepercayaan tradisional masyarakat Tionghoa, Taoisme, dan agama Buddha aliran Tanah Suci. Pada v...