Distribuição de graus
|
Read other articles:

Rugby playerDaniel DubrocaDate of birth (1954-04-25) 25 April 1954 (age 69)Place of birthAiguillon, FranceHeight1.78 m (5 ft 10 in)Weight95 kg (209 lb)Rugby union careerPosition(s) Hooker / PropAmateur team(s)Years Team Apps (Points) Agen ()International careerYears Team Apps (Points)1979–1988 France 33 (8)Coaching careerYears Team1990–19911994–1997 FranceAgen Daniel Dubroca (born 25 April 1954) is a former French national rugby union player and coach. He p...

Pakta Praha Nama panjang: Pražský mír(cs)Prager Frieden(de) Kastil PrahaDitandatangani30 May 1635LokasiKastil Praha, BohemiaPenanda tangan Kekaisaran Romawi Suci Elektorat SachsenPihakLiga KatolikLiga Heilbronn Perdamaian Praha, Pražský mír (Ceko), Prager Frieden (Jerman), ditandatangani pada 30 Mei 1635, mengakhiri partisipasi Sachsen dalam Perang Tiga Puluh Tahun. Istilah-istilah tersebut kemudian menjadi dasar dari Perdamaian Westfalen di tahun 1648. Pangeran Jerman lainnya...

دكتور[1] يوجين شيفر (بالألمانية: Eugen Schiffer) معلومات شخصية الميلاد 14 فبراير 1860 فروتسواف الوفاة 5 سبتمبر 1954 (94 سنة) برلين الغربية مواطنة ألمانيا الشرقية مناصب الحياة العملية المدرسة الأم جامعة فروتسوافجامعة توبنغنجامعة لايبتزغ المهنة سياسي،...

Dipartimenti del Nicaragua I dipartimenti del Nicaragua (in spagnolo: departamentos) costituiscono la suddivisione territoriale di primo livello del Paese e sono pari a 15; ad essi sono equiordinate due regioni autonome. I dipartimenti e le regioni autonome comprendono a loro volta più comuni. Nel 1986 la nuova costituzione riconobbe l'autonomia dell'allora dipartimento di Zelaya, che comprendeva la parte orientale del paese. Il dipartimento fu poi suddiviso in due regioni autonome, amminist...

You can help expand this article with text translated from the corresponding article in German. (March 2021) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedi...

Ярослав Харциз Загальна інформаціяПовне ім'я Ярослав Сергійович ХарцизГромадянство УкраїнаНародився 7 травня 1997(1997-05-07) (26 років)ХарківВагова категорія Перша напівсередняЗріст 175 смПрофесіональна кар'єраПерший бій 15 квітня 2023Боїв 3Перемог 3Перемог нокаутом 2Поразок ...

2001 Telugu film by Krishna Vamsi MurariFilm posterDirected byKrishna VamsiWritten byKrishna Vamsi(story & screenplay) Dialogue bySobhan Produced byN Devi PrasadRamalingeswara RaoGopi NandigamStarringMahesh BabuSonali BendreLakshmiSukumariKaikala SatyanarayanaGollapudi Maruthi RaoCinematographyC. RamprasadEdited byKrishna VamsiMusic byMani SharmaProductioncompanyRam Prasad ArtsRelease date 17 February 2001 (2001-02-17) Running time182 minutesCountryIndiaLanguageTelugu Murar...

Australian rugby coach and former player Rugby playerMichael CheikaCheika representing AustraliaDate of birth (1967-03-04) 4 March 1967 (age 56)Place of birthSydney, New South Wales, AustraliaSchoolMarcellin CollegeNotable relative(s)Adam Doueihi (cousin)Rugby league careerCoaching careerYears Team2020 Sydney Roosters (advisor)2020–2022 Lebanon Correct as of 15 May 2023Rugby union careerPosition(s) Number 8Current team Argentina (head coach)Senior careerYears Team Apps (Points)198...

Ghanaian politician Hon.Muntaka Mohammed MubarakMPMember of Ghanaian Parliament for Asawase ConstituencyIncumbentAssumed office 21 April 2005Preceded byGibril Adamu MohammedMinister for Youth and SportsIn officeJanuary 2009 – 25 June 2009PresidentJohn Atta MillsPreceded byNana AkomeaSucceeded byAbdul-Rashid Pelpuo Personal detailsBornMuntaka (1971-10-17) 17 October 1971 (age 52)NationalityGhanaianPolitical partyNational Democratic CongressSpouseMeimuna Ezideen Abdul WahabR...

Minatori Sports HallSalla e Sporteve Minatori (sq)Minatori Sports Hall after renovation in 2016LocationMitrovica, KosovoCoordinates42°53′27″N 20°52′02″E / 42.890908°N 20.867235°E / 42.890908; 20.867235OwnerMitrovica MunicipalityCapacity3,000[1]Record attendance3,500[2]ConstructionBuilt1984Opened1984Renovated2013TenantsKB TrepçaKH TrepçaFC Trepça (futsal) Minatori Sports Hall is a multi–use sports hall in Mitrovica, Kosovo which is ...

Main battle tank Altay Altay T1 demonstrationTypeMain battle tankPlace of originTurkeyService historyIn service2025 (expected)[1]Used byTurkish Land Forces[2]Production historyDesignerOtokar (design and development including prototypes)[3][4]BMC (main contractor and responsible for further developments)[5]Aselsan (sub-systems and fire control system)[5][6]MKEK (main gun system)[2][5]Roketsan (armor pac...

United States historic placeBuckman TavernU.S. National Register of Historic PlacesU.S. National Historic Landmark Buckman Tavern, Lexington, MassachusettsShow map of MassachusettsShow map of the United StatesLocation1 Bedford Street, Lexington, MassachusettsCoordinates42°26′57″N 71°13′47″W / 42.4493°N 71.2297°W / 42.4493; -71.2297Builtca. 1709–1710[chronology citation needed]ArchitectBenjamin MuzzeyArchitectural styleFederalNRHP referen...

2008 film by Erik Van Looy LoftTheatrical release posterDirected byErik Van LooyWritten byBart De PauwProduced byHilde De LaereStarring Koen De Bouw Filip Peeters Bruno Vanden Broucke Matthias Schoenaerts Koen De Graeve Veerle Baetens Marie Vinck An Miller Tine Reymer Wine Dierickx Maaike Cafmeyer Charlotte Vandermeersch Dirk Roofthooft Sara de Roo Gene Bervoets Jan Decleir CinematographyDanny ElsenEdited byPhilippe RavoetMusic byWolfram de MarcoProductioncompanyWoestijnvisDistributed byIndep...

Hastings-on-Hudson Union Free School District is a school district headquartered in Hastings-on-Hudson, New York. Its boundary includes Hastings-on-Hudson.[1] History This section needs expansion. You can help by adding to it. (April 2023) Tony Sinanis became the superintendent in 2017.[2] Demographics In 2018, 77% of the district's students were non-Hispanic white.[3] Schools Hastings High School Hastings High School Farragut Middle School The middle school began a co...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: European Tour 1995 – news · newspapers · books · scholar · JSTOR (July 2011) (Learn how and when to remove this template message) 1995 EP by DefianceEuropean Tour 1995EP by DefianceReleased1995 (1995)GenreStreet punk, anarcho-punkLength11:01LabelConsensus RealityDef...

Un eroe del nostro tempoTitolo originaleГерой нашего времени Frontespizio della prima edizione AutoreMichail Jur'evič Lermontov 1ª ed. originale1840 Genereromanzo Lingua originalerusso Modifica dati su Wikidata · Manuale Un eroe del nostro tempo (in russo Герой нашего времени?; tradotto in italiano anche con il titolo Un eroe dei nostri tempi) è un romanzo di Michail Jur'evič Lermontov pubblicato a puntate sugli Annali patrii o Memorie patriottich...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Kejaksaan Negeri Prabumulih merupakan Lembaga Pemerintah yang melaksanakan kekuasaan Negara di bidang Penuntutan serta Kewenangan Lain berdasarkan Undang-Undang Republik Indonesia Kejaksaan Republik Indonesia, yang berkedudukan di Prabumulih, Provinsi ...

Questa voce sull'argomento calciatori ghanesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Ibrahim Abdul Razak Nazionalità Ghana Altezza 180 cm Calcio Ruolo Centrocampista, attaccante Termine carriera luglio 2016 Carriera Giovanili Hapoel Ra'ananaMighty J.K. Club AalborgMalit Squadre di club1 1999 Liberty Prof.? (?)1999-2000 Aalborg? (?)2000-2001 Castelfiorentino9 (1)...

Square in Old Havana, Cuba Plaza Vieja, Havana The Plaza Vieja (lit. 'Old Square') is a plaza located in Old Havana, Cuba. The plaza and its surroundings are also one of the seven consejos populares (wards) of the municipality of Old Havana.[1] It has a residential population of 17,426.[1] Overview The plaza was originally called Plaza Nueva (New Square).[2] It emerged as an open space in 1559, after the Plaza de Armas and San Francisco. In colonial times it ...
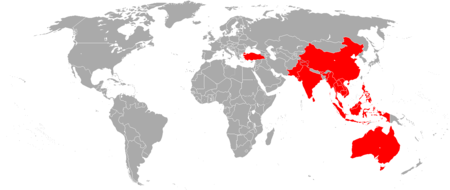
Mensiang Mensiang, Actinoscirpus grossusdi rawa pegunungan Tanah Kampung, Sungai Penuh Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monocots (tanpa takson): Commelinids Ordo: Poales Famili: Cyperaceae Genus: Actinoscirpus(Ohwi) R.W.Haines & Lie Spesies: A. grossus Nama binomial Actinoscirpus grossus(L.f.) Goetgh. & D.A.Simpson[1] Agihan mensiang (warna merah) Sinonim Scirpus grossus L.f.[2] (basionym) Sinonim selengkapnya, lih...












