Ciało algebraicznie domknięte
|
Read other articles:

Контактные линзы Надетая контактная линза Установка и снятие мягких контактных линз Контактные линзы — линзы, которые надеваются непосредственно на роговицу глаза. Чаще всего они используются с целью коррекции нарушений зрения: близорукости (миопии), дальнозоркост�...

1942 film A-Haunting We Will GoTheatrical release posterDirected byAlfred L. WerkerWritten byLou BreslowStanley RauhProduced bySol M. WurtzelStarringStan LaurelOliver HardyDante the MagicianSheila Ryan John SheltonCinematographyGlen MacWilliamsEdited byAlfred DayMusic byDavid ButtolphCyril J. MockridgeDistributed by20th Century FoxRelease dateAugust 7, 1942Running time66' 40CountryUnited StatesLanguageEnglish A-Haunting We Will Go is a 1942 Laurel and Hardy feature film released by 20th Centu...

Erik LaRay Harvey (2019) Erik LaRay Harvey (* 1972 in Bainbridge, Georgia) ist ein US-amerikanischer Schauspieler. Bekanntheit erlangte er vor allem durch die Fernsehserie Boardwalk Empire und durch seine Rolle als Willis Stryker alias Diamondback in der Netflix-Serie Marvel’s Luke Cage. Inhaltsverzeichnis 1 Leben und Karriere 2 Filmografie (Auswahl) 3 Weblinks 4 Einzelnachweise Leben und Karriere Erik LaRay Harvey wurde im US-Bundesstaat Georgia geboren und wuchs in Washington, D.C. auf. E...

Sohrab Moradi Sohrab Moradi Halterofilismo Nome completo Sohrab Moradi Nascimento 22 de setembro de 1988 (35 anos)Irã Nacionalidade iraniano(a) Medalhas Jogos Olímpicos Ouro Rio 2016 -94 kg Sohrab Moradi (22 de setembro de 1988) é um halterofilista iraniano, campeão olímpico. Carreira Sohrab Moradi competiu na Rio 2016, na qual conquistou a medalha de ouro na categoria até 94kg.[1] Referências ↑ «Perfil na Rio 2016». Consultado em 27 de agosto de 2015 vde Campeões ol

مطار لوس أنجلوس الدولي مطار لوس أنجلوس الدولي إياتا: LAX – ايكاو: KLAX موجز المالك لوس أنجلوس يخدم منطقة لوس أنجلوس الكبرى البلد الولايات المتحدة الموقع لوس أنجلوس، كاليفورنيا الارتفاع 126 قدم إحداثيات 33°56′33″N 118°24′29″W / 33.9425°N 118.408056°W / 33.9425; -118.408056 ال�...

Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang netral dan sesuai dengan kebijakan Wikipedia. (September 2021) Extreme MildJenis produkRokokPemilikJapan TobaccoProdusenPT Karya Dibya MahardhikaNegaraIndonesiaDiluncurkan1996; 26 tahun lalu (1996)Dihentikan2018PasarIndonesiaJargonArtikan Di...

African hybrid knife/axe This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mambele – news · newspapers · books · scholar · JSTOR (February 2019) (Learn how and when to remove this template message) Variations of the mambele across the top row A mambele is a form of hybrid knife/axe in central and southern Afri...
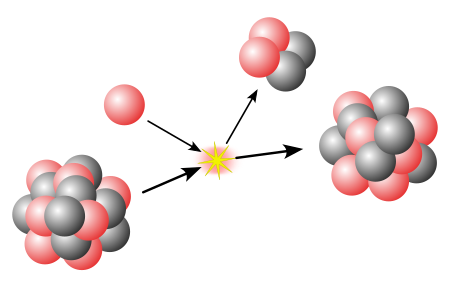
Core atomic nucleus surrounded by orbiting protons or neutrons Nuclear physics Nucleus Nucleons p n Nuclear matter Nuclear force Nuclear structure Nuclear reaction Models of the nucleus Liquid drop Nuclear shell model Interacting boson model Ab initio Nuclides' classification Isotopes – equal Z Isobars – equal A Isotones – equal N Isodiaphers – equal N − Z Isomers – equal all the above Mirror nuclei – Z ↔ N Stable Magic Even/odd Halo Borromean Nuclear stability ...

صفاقةمعلومات عامةنوع المبنى موقع أثري تاريخيالمكان منطقة الرياض - محافظة الدوادميالبلد السعوديةالانتماء العصر الحجري القديم أشولينيةتعديل - تعديل مصدري - تعديل ويكي بيانات صفاقة تقع جنوب شرق محافظة الدوادمي على بعد 280 كم من مدينة الرياض وسط المملكة العربية السعودية. ه...

У этого термина существуют и другие значения, см. Рахат. АО «ЛОТТЕ Рахат» Тип Акционерное общество Листинг на бирже KASE: RAHT Год основания СССР Казахская ССР: Алматы, 1942 Прежние названия «Алматинская кондитерская фабрика» Основатели Правительство Казахской ССР Распо...

This article is about the British locality. For the Canadian locality, see Rural Municipality of Elmsthorpe No. 100. Human settlement in EnglandElmesthorpeThe partially ruined St Mary's Church, ElmesthorpeElmesthorpeLocation within LeicestershirePopulation509 (2011)OS grid referenceSP4696Civil parishElmesthorpeDistrictBlabyShire countyLeicestershireRegionEast MidlandsCountryEnglandSovereign stateUnited KingdomPost townLeicesterPostcode districtLE9PoliceLeicesters...

The opening lines of Pascon agan Arluth in the 1826 edition The anonymous poem Pascon agan Arluth is the oldest complete literary work in the Cornish language, dating from the 14th century. The modern title (it is untitled in the oldest manuscript) means The Passion of Our Lord, but the poem has also been published as Mount Calvary.[1][2] Date, manuscripts and authorship Pascon agan Arluth dates from the 14th century;[note 1] it pre-dates the Ordinalia, a cycle of thre...

South Korean badminton player In this Korean name, the family name is Bae. Badminton playerBae Yeon-juBae Yeon-ju at the 2013 French Super SeriesPersonal informationBirth name배연주CountrySouth KoreaBorn (1990-10-26) 26 October 1990 (age 33)Masan, South Gyeongsang Province, South KoreaHeight1.66 m (5 ft 5 in)Weight53 kg (117 lb)HandednessLeftWomen's singlesCareer record236 wins, 148 lossesHighest ranking5 (23 October 2016) Medal record Women's badmin...

2004 novel by Jonathan Trigell Boy A First editionAuthorJonathan TrigellCountryUnited KingdomLanguageEnglishPublisherSerpent's TailPublication date2004Pages248Awards John Llewellyn Rhys Prize Waverton Good Read Award ISBN978-1-84668-662-7OCLC236175543 Boy A is the debut novel by Jonathan Trigell, which was first published in 2004. Premise The book is the story of a child criminal released into society as an adult, taking its title from the court practice of concealing the identity of child de...

1862 New Jersey gubernatorial election ← 1859 November 4, 1862 1865 → Nominee Joel Parker Marcus Lawrence Ward Party Democratic National Union Popular vote 61,307 46,710 Percentage 56.8% 43.2% County resultsParker: 50–60% 60–70% 70–80% Ward: 50-60% 60–70% Governor before election Charles Smith Olden Repu...

Shands redirects here. For other uses, see Shands (disambiguation). This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (June 2023) (Learn how and when to remove this template message) Hospital in Florida, United StatesUF Health Shands HospitalUF HealthGeographyLocation1600 SW Archer Road, Gainesville, Florida, Flori...

American actress (1924–2003) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fritzi Burr – news · newspapers · books · scholar · JSTOR (September 2016) (Learn how and when to remove this template message) Fritzi BurrBurr on Sanford and Son in 1976Born(1924-05-31)May 31, 1924Philadelphia, Pennsylvania, U.S....

Site of historical ruins in Xinjiang This article is about the historical kingdom. For the district in Turpan City, see Gaochang, Turpan. For the Uyghur kingdom, see Qocho. For other uses, see Gaochang (disambiguation). Gaochang高昌قۇچۇThe Buddhist stupa of Gaochang ruinsShown within XinjiangShow map of XinjiangGaochang (China)Show map of ChinaLocationXinjiang, ChinaCoordinates42°51′10″N 89°31′45″E / 42.85278°N 89.52917°E / 42.85278; 89.52917TypeSettl...

You can help expand this article with text translated from the corresponding article in Japanese. (December 2009) Click [show] for important translation instructions. View a machine-translated version of the Japanese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English W...

María Luisa Mayol Información personalNombre de nacimiento María Luisa Mayol LabbéApodo MaluNacimiento 20 de febrero de 1981 (43 años)Santiago, ChileResidencia Madrid, EspañaNacionalidad ChilenaFamiliaCónyuge Luis Tosar (matr. 2015)Pareja Boris Quercia (2004–2014) Luis Tosar (2014–presente)Hijos León Tosar MayolLuana Tosar MayolInformación profesionalOcupación Actriz, conductora de televisiónAños activa 2005-presente[editar datos en Wikidata] María Lui...













![{\displaystyle F[X_{1},X_{2},\dots ,X_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbde69a9f08916db3703aec7bf94382f32f72352)




























