지도 투영법(地圖投影法)은 위선과 경선으로 이루어진 지구상의 가상적 좌표를 평면상에 옮기는 방법을 가리킨다. 지구는 구체이기 때문에, 아무리 작은 공간의 지도를 작성한다 할지라도 그 왜곡을 피할 수 없다. 따라서 투영법은 이 왜곡을 처리하는 방법이라고 정의할 수 있다.
성질을 보전하는 것에 따른 분류
지도에서 왜곡은 방향(방위)·각도·거리·넓이(면적)의 측면에서 일어나는데 이중 일부 성질을 보전할 수 있다. 이러한 성질을 보전하는 도법에는 다음 종류가 있다.
정각도법(正角圖法, angular projection) : 경선과 위선간의 각도 관계가 정확하게 나타나는 도법이다. 대륙의 형태가 지구본과 비슷하게 나타나기 때문에 정형도법(正形圖法, conformal projection)이라고도 부른다. 좁은 지역에서는 정형성이 유지되지만 대륙 단위 이상의 넓은 지역에서는 형태의 왜곡이 발생한다.
정거도법(正距圖法, equidistant projection) : 중심점으로부터 거리가 정확하게 나타난 도법이다.
정적도법(正積圖法, equal area projection) : 넓이가 정확하게 나타나는 도법이다. 어느 지역에서건 지구상 면적과 지도상 면적이 동일하게 나타나지만, 지도의 중앙에서 주변부로 갈수록 왜곡이 심해진다. 분포도 작성에 주로 이용된다.
방위도법(方位圖法, azimuthal projection) : 중심점으로부터 방향이 정확하게 나타나는 도법이다. 따라서 이 도법으로 그려진 지도에서는 중심과 다른 어떤점의 직선 경로가 최단 경로와 같다. 방위는 정각성, 정적성, 정거성 중 하나의 성질과 함께 보전하도록 지도투영법을 만들 수 있다.
어떤 성질도 보전하지 않지만 각각의 성질의 왜곡을 최소화한 도법도 있다. 이를 절충도법(折衷圖法, compromise projection)이라고 한다.
이 외에도 지도의 제작 방식에 따라 방위도법·원통도법·원추도법·임의도법으로 분류되기도 한다.
투영 방법이나 보전하는 성질을 기반으로 명명된 도법 유형을 변형하는 경우 의(擬, pseudo)를 앞에 붙인다.
단열도법(斷熱圖法, interrupted projection)은 경선을 쪼개서 표현한 지도다.
역방위도법(逆方位圖法, retroazimuthal projection) : 중심점으로의 방향이 정확하게 나타나는 도법이다.
방위도법
평사도법심사도법방위정거도법
방위도법은 지구본과 투영면이 접하는 점이 중심이 된다. 이 중심에서 방사상으로 긋는 직선은 모두 대권과 일치하며 방향이 정확하다.
정사도법(正射圖法, orthographic projection) : 지구를 멀리서 바라볼 때와 같은 지도를 그릴 수 있는데, 반구 이상은 그릴 수 없다. 중심부에서는 대륙의 모양이 비교적 바르게 나타나지만, 주변부에서는 그 중심에 따라 극 중심일 경우 위선의 간격이 좁아지고, 적도 중심의 경우 경선과 위선의 간격이 모두 좁아지는 등 모양의 왜곡이 심해진다. 장식용 반구도를 그릴때 주로 사용된다.
평사도법(平射圖法, stereographic projection) : 투영면을 지구본의 한 점에 접하게 하고 접점의 대척점을 시점으로 하여 경선과 위선을 투시하는 도법으로, 반구도 제작에 쓰인다. 중심이 어디에 놓이건 경선과 위선의 간격이 동일한 비율로 넓어지기 때문에 각도 관계가 정확하게 나타난다. 극 중심의 고위도 지역 지도 제작에 많이 쓰인다.
심사도법(心射圖法, gnomonic projection) : 지구 중심에 시점을 두고 투시하는 도법이다. 반구 전체를 나타낼 수 없으며 주변부로 갈수록 축척 및 형태의 왜곡이 매우 심해진다. 그러나 임의의 두 점 간을 직선으로 연결하면 대권과 일치하기 때문에 항공용 지도로 많이 쓰인다. 대권도법(大圈圖法)이라고도 한다.
방위정거도법(方位正距圖法, azimuthal equidistant projection) : 지도의 중심에서 모든 지점까지의 직선거리가 정확하게 나타나도록 임의로 경선과 위선의 간격을 조절한 도법이다. 이 도법은 특정 점(주로 도시)을 기준으로 한 세계지도 제작에 흔히 사용된다. 중심점에서 출발한 직선은 항상 대권이 된다.
방위정적도법(方位正積圖法, azimuthal equal area projection) : 독일의 요한 람베르트가 1772년 발표한 도법이다. 경선은 극 중심에서 방사상으로 뻗어 있고 위선은 극을 중심으로 동심원을 이룬다. 지도상에서 일정한 간격의 경선과 위선으로 둘러싸인 부분은 모두 면적이 지구본과 동일하다. 국토가 넓은 국가나 대륙을 나타내는 지도에 쓰인다.
원통도법
메르카토르도법으로 그린 세계지도. 메르카토르 도법으로 그린 지도에서는 항정선이 직선으로 나타난다. 항해용 지도에 주로 쓰인다.횡축 메르카토르도법
원통도법(圓筒圖法, cylindrical projection)은 세계지도를 직사각형으로 그리며 적도를 중심에 놓을 때 경선은 간격이 같고 위선은 평행하게 그려지는 도법을 가리킨다. 이것은 지구본을 원통으로 둘러싸고 그 원통으로 옮긴 뒤, 원통을 펼치는 것으로 이해할 수 있다.
원통도법에서 위도를 φ라고 할 때 경선은 sec φ배로 확대된다. 원통도법은 위선이 얼만큼 확대되는지에 따라 다음과 같이 분류된다.
위선의 배율이 경선과 같은 경우: 정각 도법이 되어 메르카토르도법(Mercator projection)이라고 불린다. 1569년네덜란드의 게르하르두스 메르카토르가 발표했으며 적도에서 멀어질수록 축척 및 면적이 크게 확대되어 극을 표시할 수 없는 단점이 있다.
고위도에서 위선이 경선보다 더 크게 확대되는 경우: 경선의 배율의 제곱으로 확대되는 원통중심도법(圓筒中心圖法, central cylindrical projection)이 있다. 이 도법에서 적도에 원통을 접하게 한 뒤 구의 중심을 기준으로 원통에 투영시킨다. 고위도로 갈 수록 왜곡이 더욱 심하여 쓰이지 않는다.
위도가 높아질수록 위선이 확대되지만, 경선의 확대율보다는 작은 경우: 밀러 도법, 갈 평사 원통 도법과 같은 도법이 있다. 정적성과 정각성은 없지만, 고위도지방의 왜곡이 메르카토르도법에 비해 적다.
위도가 높아져도 위선은 확대되지 않는 경우: 등장방형도법(Equirectangular projection)이다.
위선의 확대율과 경선의 확대율이 반비례 하는 경우:넓이가 일정하므로 원통정적도법(圓筒正積圖法, cylindrical equal area projection)이 된다. 원통정적도법은 위선, 경선의 축척이 일치하는 위도에 따라 여러가지로 분류된다. 적도를 기준으로 한 경우를 람베르트 정적원통도법이라고 한다. 람베르트 정적 원통 도법은 지구 적도에 원통을 접하게 한 뒤, 지구의 점을 같은 높이에 있는 원통의 점으로 옮기어 얻을 수 있다. 즉, 위선의 높이는 같은 경선의 점을 기준으로 정사 도법에 따라 옮겼을때의 거리와 같다.
투영 중심에 따른 분류: 원통 도법은 투영의 중심이 되는 원형의 면에 대해 정확하다. 이런 면은 보통 적도이지만, 경선으로 기울이거나(횡축) 또는 임의의 지구 중심을 지나는 면을 중심으로 기울이기도(사축) 한다. 지구는 실제로는 회전타원체 이기 때문에 그에 맞는 다양한 공식이 있다. 가장 널리 쓰이는 것은 메르카토르 도법의 횡축 투영이다.
횡축 메르카토르 도법(橫軸-, transverse Mercator projection) : 적도 대신 지구본을 옆으로 뉘어서 투영하는 메르카토르도법이다. 지도의 축척은 중앙경선을 따라서만 정확하다. 중앙경선을 중심으로 하는 좁은 경도대에서는 축척의 증가가 매우 작기 때문에 정각성이 뛰어난 대축척지도에 유용하게 쓰인다. 대한민국에서 사용되는 1:50,000 지도는 모두 이 방식을 이용해 제작되었다.
사축 메르카토르 도법(斜軸-, oblique Mercator projection) : 적도 대신 지구본을 기울여서 투영하는 메르카토르도법이다.
의원통도법
의원통도법(擬圓筒圖法, pseudo cylindrical projection)은 원통도법의 고위도의 경선길이를 바꾸어 (일반적으로 줄인) 만든 도법이다. 위선은 직선이며 경선은 중앙경선은 직선이며 같은 위도를 가진 다른 경도의 점은 경도에 비례하여 떨어져 있다.
시뉴소이드도법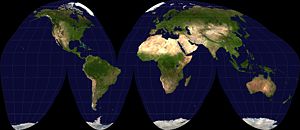호몰로사인도법에케르트 제4도법
시뉴소이드 도법(sinusoidal projection) : 정적도법으로 위선이 실제와 같은 등간격 평행선으로 되어 있고 그 길이도 실제와 같다. 경선은 직선인 중앙경선을 기점으로 등간격의 사인 곡선을 이룬다. 이 때문에 위선의 축척이 정확하고 일정한 위도대에서 일정한 간격의 경선과 위선으로 둘러싸인 부분은 모두 같다. 세계지도를 그릴 경우 주변부의 형태 왜곡이 심하지만 중심부는 왜곡이 적기 때문에 남아메리카·아프리카 등의 대륙지도나 동남아시아와 같은 동서로 긴 형태의 지도에 적합하다.
몰바이데 도법(Mollweide projection 혹은 homolographic projection "등비율 도법") : 1805년 독일의 카를 몰바이데(de)가 개발한 정적도법이다. 지구본의 반구를 원으로 그린 후 나머지 반구를 둘로 나누어 그 바깥쪽으로 연장했기 때문에 타원형의 모양을 지닌다. 지도 중앙부를 비교적 정확하게 나타낼 수 있고 주변부의 왜곡도 덜 심하기 때문에 각 대륙들도 적절히 배열된다. 세계의 각종 분포도나 아프리카·북아메리카 등의 대륙 지도, 유럽 중심의 세계 지도에 많이 사용된다.
호몰로사인 도법(homolosine projection) : 1923년 미국의 존 폴 구드가 개발한 정적도법으로 구드도법이라고도 한다. 고위도 왜곡이 적은 몰바이데도법과 저위도 왜곡이 적은 시뉴소이달도법을 합쳐놓은 도법으로 남·북위 40'선을 기준으로 고위도는 몰바이데도법 저위도는 시뉴조이달도법을 적용했다. 세계의 각종 분포도에 많이 쓰였으나 바다가 잘리기 때문에 근래에는 사용이 적어졌다.
에케르트 제4도법(Eckert IV projection) : 독일의 막스 에케르트가 고안한 6개의 도법 중 4번째 도법으로 정적도법이다. 중앙 경선은 직선, 외곽의 두 경선은 원호, 그 밖의 경선은 모두 등간격의 타원호이다. 중앙경선은 적도의 절반으로, 고위도지방의 왜곡을 완화했다. 바다를 자르지 않고도 모든 대륙을 비교적 바르게 나타낼 수 있어 세계 각종 분포도에 많이 쓰인다.
원추도법
람베르트 정각원추도법
원추도법(圓錐圖法) 혹은 원뿔도법(conic projection)은 지구본의 중심에서 지구본에 씌운 원추에 경선과 위선을 투영하고 이를 다시 펼쳐 평면으로 만드는 도법이다. 보통 북극이나 남극의 위에 중점을 두고 중위도 지역을 보여주는 지도에 쓰인다. 원래의 원추 도법에서 원추의 중심으로부터 방향은 실제 지구에서의 방향보다 압축되므로, 극이 중심인 경우 경선은 등각간격의 직선이다.
투시원추도법(透視圓錐圖法, perspective conic projection) : 한 개의 위선을 지구본에 접하도록 원추를 씌우고 투시한 도법이다. 표준 위선에선 축척이 정확하나 남·북으로 멀어질수록 축척이 확대된다.
람베르트 정각원추도법(람베르트正角圓錐圖法, Lambert conformal conic projection) : 표준위선이 2개인 원추도법을 개량한 것으로 위선의 간격을 조절해 각도의 왜곡을 없앴다. 그리기 쉬우며 대축척 지도에서 개별 도엽들이 잘 맞춰진다. 지도상의 직선이 대권과 매우 유사하므로 항공용 지도로 사용된다.
절충 도법(折衷圖法, compromise projection)은 어떤 성질도 보전하지 않지만 각각의 성질의 왜곡을 최소화한 도법이다.
로빈슨 도법
빈켈 트리펠 도법(Winkel tripel 圖法): 1913년 독일 사람 오스발트 빈켈이 고안해낸 것이다. 극을 점이 아닌 직선으로 표시하는 것은 에케르트도법과 비슷하지만, 적도 이외의 위선이 적도에 대하여 활 모양의 좁은 곡선인 점이 다르다. 정적·정각은 아니지만 면적의 일그러짐이나 각의 일그러짐이 전체적으로 작기 때문에 세계 지도에 많이 이용된다.
