![]() ś®ôśļĖÁ∑ĮÁ∑ö„āíŚĆóÁ∑Į20¬įŚŹä„Ā≥ŚĆóÁ∑Į50¬į„Āꍮ≠Śģö„Āó„Āü„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē
ś®ôśļĖÁ∑ĮÁ∑ö„āíŚĆóÁ∑Į20¬įŚŹä„Ā≥ŚĆóÁ∑Į50¬į„Āꍮ≠Śģö„Āó„Āü„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē
 ś®ôśļĖÁ∑ĮÁ∑ö„āíŚĆóÁ∑Į15¬įŚŹä„Ā≥ŚĆóÁ∑Į45¬į„Āꍮ≠Śģö„Āó„ÄĀ„ÉÜ„ā§„āĹ„Éľ„ĀģśĆáÁ§ļś•ēŚÜÜ„ā횼ė„Āó„Āü„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē
ś®ôśļĖÁ∑ĮÁ∑ö„āíŚĆóÁ∑Į15¬įŚŹä„Ā≥ŚĆóÁ∑Į45¬į„Āꍮ≠Śģö„Āó„ÄĀ„ÉÜ„ā§„āĹ„Éľ„ĀģśĆáÁ§ļś•ēŚÜÜ„ā횼ė„Āó„Āü„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē
 „āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē„Āę„āą„āčŚúįŚõ≥„Āģšĺč
„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē„Āę„āą„āčŚúįŚõ≥„Āģšĺč
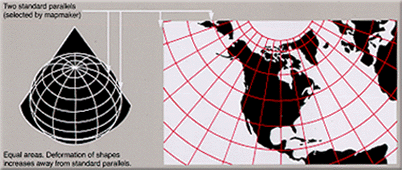 „āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē„ĀĮťĚĘÁ©ć„āíś≠£ÁĘļ„Āꍰ®Á§ļ„Āô„āč„ĀĆ„ÄĀŚĹĘÁä∂„ĀĮś≠™„āíšľī„ĀÜ„Äā
„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē„ĀĮťĚĘÁ©ć„āíś≠£ÁĘļ„Āꍰ®Á§ļ„Āô„āč„ĀĆ„ÄĀŚĹĘÁä∂„ĀĮś≠™„āíšľī„ĀÜ„Äā
„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ēÔľą„āĘ„Éę„Éô„Éę„āĻ„Āõ„ĀĄ„Āõ„Āć„Āą„āď„Āô„ĀĄ„Āö„ĀĽ„ĀÜ„ÄĀAlbers Equal-Area Conic ProjectionԾȄĀ®„ĀĮ„ÄĀŚúįŚõ≥śäēŚĹĪś≥ē„ĀģšłÄ„Ā§„Āß„ÄĀ2„Ā§„Āģś®ôśļĖÁ∑ĮÁ∑ö„āíśĆĀ„Ā§Śõ≥ś≥ē„ĀģšłÄÁ®ģ„Āß„Āā„āč„ÄāŚÜܝƟŚõ≥ś≥ē„Āß„Āā„āä„ÄĀś≠£Á©ćŚõ≥ś≥ēÔľąŤčĪŤ™ěÁȹԾȄĀß„āā„Āā„āč„Äā1805ŚĻī„Āę„ÉŹ„ā§„É≥„É™„Éí„ÉĽ„āĮ„É™„āĻ„ÉÜ„ā£„āĘ„É≥„ÉĽ„āĘ„Éę„Éô„Éę„āĻÔľą„ÉČ„ā§„ÉĄŤ™ěÁȹԾȄĀĆŤÄÉś°ą„ÉĽÁôļŤ°®„Āó„Āü„Äā
śó•śú¨„ĀģŚõĹŚúüŚúįÁźÜťôĘ„ĀĆÁôļŤ°Ć„Āô„āč„ÄĆŚÖ®ŚõĹťÉĹťĀďŚļúÁúĆŚłāŚĆļÁĒļśĚĎŚą•ťĚĘÁ©ćŤ™Ņ„Äć„Āß„ĀĮ„ÄĀŚĻ≥śąź26ŚĻīťĚĘÁ©ćŤ™Ņ„Āč„āČ„ÄĀťĚĘÁ©ćśł¨Śģö„ĀęŚĹď„Āü„āä2śú¨„Āģś®ôśļĖÁ∑ĮÁ∑ö„āíŚĆóÁ∑Į33¬įŚŹä„Ā≥ŚĆóÁ∑Į44¬į„ÄĀšł≠Ś§ģÁĶĆÁ∑ö„āíśĚĪÁĶĆ135¬į„Ā®„Āô„āč„āĘ„Éę„Éô„Éę„āĻś≠£Á©ćŚÜܝƟŚõ≥ś≥ē„āíśé°ÁĒ®„Āó„Ā¶„ĀĄ„āč[3]„Äā
śäēŚĹĪś≥ē„ĀģÁČĻŚĺī
„Āď„ĀģśäēŚĹĪś≥ē„Āę„āą„āä„ÄĀŚúįÁźÉ„ĀĮŚÜܝƟŚŹį„ĀģŚĀīťĚĘ„ĀģŚĪēťĖčŚõ≥„ĀęśäēŚĹĪ„Āē„āĆ„ÄĀÁ∑ĮÁ∑ö„ĀĮŚÜܝƟŚŹį„Āģť†āÁāĻ„ĀģŚĪēťĖčÁāĻ„āíšł≠ŚŅÉ„Ā®„Āô„ā茟ƌŅÉŚÜÜŚľßÁä∂„Āę„ÄĀÁĶĆÁ∑ö„ĀĮŚĹ≤ŚĪēťĖčÁāĻ„Āč„āČśĒĺŚįĄÁä∂„Ā꜏Ź„Āč„āĆ„āč„Äāś•ĶÁāĻ„ĀĮÁ∑ĮÁ∑öŚÜÜŚľßÁ姄Ā®ŚźĆŚŅÉ„ĀģŚÜÜŚľß„ĀłśäēŚĹĪ„Āē„āĆ„āč„Āď„Ā®„Āę„Ā™„āč„ÄāťęėÁ∑ĮŚļ¶ŚĀī„Āģś®ôśļĖÁ∑ĮŚļ¶„āí90¬į„Āꍮ≠Śģö„Āó„Āü„āā„Āģ„ĀĆ„É©„É≥„Éô„Éę„Éąś≠£Á©ćŚÜܝƟŚõ≥ś≥ē„ĀęÁõłŚĹď„Āô„āč„Äā
śäēŚĹĪ„ĀģŤ°®ŚľŹ
šĽ•šłč„Āß„ĀĮŚúįÁźÉ„āíŤĶ§ťĀďŚćäŚĺĄ a „ÄĀťõĘŚŅÉÁéá e „ĀģśČĀÁźÉŚõ썼ʜ•ēŚÜÜšĹď„Ā®„Āó„Ā¶Ť™¨śėé„Āô„āč„Äā
Śļßś®ôŚéüÁāĻ„āíŚÜܝƟŚŹį„Āģť†āÁāĻ„ĀęÁõłŚĹď„Āô„āčśäēŚĹĪÁāĻ„Āę„Ā®„āä„ÄĀŚĹ≤ŚéüÁāĻ„Āč„āČŤĶ§ťĀď„ĀłŚźĎ„Āč„ĀÜśĖĻŚźĎ„āíś≠£śĖĻŚźĎ„Ā®„Āó„Āüšł≠Ś§ģÁĶĆÁ∑ö„āíXŤĽł„Āꍮ≠Śģö„Āó„ÄĀŚĹ≤šł≠Ś§ģÁĶĆÁ∑ö„ĀģÁĶĆŚļ¶„āíλ0 „Ā®„Āô„āč„Ā®„Āć„ÄĀ2„Ā§„Āģś®ôśļĖÁ∑ĮŚļ¶ φ1„ÄĀφ2 „ĀęŚĮĺ„Āó„Ā¶„ÄĀÁ∑ĮŚļ¶ φ„ÄĀÁĶĆŚļ¶ λ „ĀģÁāĻ„āí


„ĀęśäēŚĹĪ„Āô„āč„Äā„Āü„Ā†„Āó„ÄĀ

 „ÄÄÔľąŤĶ§ťĀď„Ā®Á∑ĮŚļ¶ φ „ĀģŚĻ≥Ť°ĆŚúŹ„ĀęśĆü„Āĺ„āĆ„ĀüÁ∑ĮŚļ¶ŚłĮ„ĀģťĚĘÁ©ć[4]ÔľČ
„ÄÄÔľąŤĶ§ťĀď„Ā®Á∑ĮŚļ¶ φ „ĀģŚĻ≥Ť°ĆŚúŹ„ĀęśĆü„Āĺ„āĆ„ĀüÁ∑ĮŚļ¶ŚłĮ„ĀģťĚĘÁ©ć[4]ÔľČ
„Āß„Āā„āä„ÄĀ ŚŹä„Ā≥
ŚŹä„Ā≥  „ĀĮ„ÄĀ„ĀĚ„āĆ„Āě„āĆÁ∑ĮŚļ¶ φ „ĀęŚĮĺ„Āô„āčŚ≠źŚćąÁ∑öśõ≤ÁéáŚćäŚĺĄŚŹä„Ā≥ŚćĮťÖČÁ∑öśõ≤ÁéáŚćäŚĺĄ„Āß„Āā„āč„Äā
„ĀĮ„ÄĀ„ĀĚ„āĆ„Āě„āĆÁ∑ĮŚļ¶ φ „ĀęŚĮĺ„Āô„āčŚ≠źŚćąÁ∑öśõ≤ÁéáŚćäŚĺĄŚŹä„Ā≥ŚćĮťÖČÁ∑öśõ≤ÁéáŚćäŚĺĄ„Āß„Āā„āč„Äā
ŤĄöś≥®
ŚŹāŤÄÉśĖáÁĆģ
- ŤŹÖťáéŚ≥įśėé ŤĎó„ÄĆŚúįŚõ≥„Äć„ÄĀŤŹÖťáéŚ≥įśėé„ÉĽŚģČšĽĀŚĪčśĒŅś≠¶„ÉĽťęėťė™ŚģŹŤ°Ć Á∑®„ÄéŚúįÁźÜÁöĄśÉÖŚ†Ī„ĀģŚąÜśěźśČčś≥ē„ÄŹŚŹ§šĽäśõłťôĘ„ÄąŚúįÁźÜŚ≠¶Ť¨õŚļß„ÄČ„ÄĀ1987ŚĻī„ÄĀ1-68ť†Ā„ÄāISBN 4-7722-1228-0„Äā
- śó•śú¨ŚúįŤ™ĆÁ†ĒÁ©∂śČÄ Á∑®„ÄéŚúįÁźÜŚ≠¶ŤĺěŚÖł śĒĻŤ®āÁČą„ÄŹšļĆŚģģśõłŚļó„ÄĀ1989ŚĻī„ÄāISBN 4-8176-0088-8„Äā
ťĖĘťÄ£ť†ÖÁõģ
Ś§ĖťÉ®„É™„É≥„āĮ