Carico critico euleriano

Si dice carico critico euleriano, per la teoria elastica della trave, quella forza di compressione il cui valore porta indefinitamente ad inflessione il solido snello su cui agisce, generando instabilità a carico di punta.

Caso asta uniforme in assenza di taglio

Descrizione

Schema statico

Si consideri un'asta realizzata con un materiale elastico lineare, soggetta ad una forza di compressione ${\displaystyle N}$ a un capo.

Se l'asta subisce un lieve sbandamento in modo che la sua linea d'asse (deformata) sia descritta da una curva nota, di equazione ${\displaystyle y(x)}$, la forza ${\displaystyle N}$ produce anche un momento ${\displaystyle Ny(x)}$, a cui si oppone il momento interno che, se si confonde la curvatura con la derivata seconda, vale ${\displaystyle EJy''(x)}$, dove E è il modulo di elasticità longitudinale.

La condizione di equilibrio, per cui la configurazione deformata sia in equilibrio con la forza esterna, impone che la somma dei momenti, interno ed esterno, sia nulla:

${\displaystyle EJy''(x)=Ny(x)\ }$

Questa è una equazione di Helmholtz per la funzione y(x), che può essere ridotta in forma canonica come l'equazione agli autovalori:

${\displaystyle y''(x)=k^{2}y(x)\ }$

in cui l'autovalore dell'operatore matematico della derivata seconda, corrisponde a:

${\displaystyle k={\sqrt {\frac {N}{EJ}}}}$

La soluzione di questa equazione è:

${\displaystyle y(x)=A\cos(kx)+B\sin(kx)\ }$

dove A e B sono costanti di integrazione, che richiedono altrettante condizioni al contorno. Si impongono quindi due condizioni di Dirichlet: ${\displaystyle y(0)=y(\lambda )=0}$: posizioniamo lo zero del sistema di riferimento in un punto indeformato, e studiamo dove la trave torna indeformata.

La lunghezza inflessa, ovvero la lunghezza d'onda stazionaria associata alla deformazione λ, non corrisponde in generale alla lunghezza semplice della trave (h): a seconda di come la trave è vincolata la lunghezza inflessa può essere superiore o inferiore alla lunghezza fisica della trave alla distanza tra due flessi nella trave deformata.

Dalla condizione ${\displaystyle y(0)=A=0}$, segue semplicemente che la prima delle due costanti è nulla.

La seconda condizione diventa allora che la lunghezza inflessa è la coordinata del punto in cui lo spostamento torna nullo: ${\displaystyle y(\lambda )=B\sin(k\lambda )=0}$, che ha due soluzioni possibili:

• se ${\displaystyle \sin(k\lambda )\neq 0}$, deve risultare ${\displaystyle B=0}$. In questo caso la soluzione dell'equazione è ${\displaystyle y(x)\equiv 0}$, ovvero la sola configurazione di equilibrio è quella indeformata.

• se ${\displaystyle \sin(k\lambda )=0}$ allora la condizione al contorno è soddisfatta per qualunque valore di B, pertanto esistono infinite configurazioni equilibrate (equilibrio indifferente).

La condizione ${\displaystyle \sin(k\lambda )=0}$ implica che ${\displaystyle k\lambda =n\pi }$, dove n indica un intero positivo. Ricordando la definizione del numero d'onda ${\displaystyle k}$, si ha che la precedente condizione è soddisfatta se

${\displaystyle {\frac {N}{EJ}}\lambda ^{2}=n^{2}\pi ^{2}}$

e questo si verifica per quei valori di N tali che

${\displaystyle N(n)=n^{2}\pi ^{2}{\frac {EJ}{\lambda ^{2}}}}$

Il più piccolo dei valori di ${\displaystyle N_{n}}$ corrisponde al passaggio da una condizione di equilibrio stabile ad una instabile. Tale valore è quello per n = 1, ed è detto il carico critico euleriano dell'asta compressa:

${\displaystyle N_{cr}=N(n=1)=\pi ^{2}{\frac {E\,J}{\lambda ^{2}}}}$

Indicando con ${\displaystyle N_{cr}}$ la forza critica. Si noti che finora non si è parlato della lunghezza reale h della trave: questa si considera nel paragrafo vincolamento.

Tensione critica

Dal carico critico ne deriva la tensione critica, cioè il valore della tensione raggiunto dall'asta quando ${\displaystyle N}$

${\displaystyle \sigma _{cr}={\frac {N_{cr}}{A}}=\pi ^{2}{\frac {EJ_{\min }}{\lambda ^{2}A}}={\frac {\pi ^{2}}{\lambda '^{2}}}E}$

ovvero, in forma adimensionale:

  ${\displaystyle {\frac {\sigma _{cr}}{E}}=\left({\frac {\pi }{\lambda '}}\right)^{2}}$

con:

${\displaystyle \lambda '={\frac {\lambda }{\rho }}}$

La quantità adimensionale ${\displaystyle \lambda '}$ viene chiamata "snellezza" dell'asta: è un parametro che dipende da forma e vincolamento della trave, corrispondente al rapporto tra lunghezza inflessa (che dipende dal vincolamento, e dalla lunghezza della trave) e raggio d'inerzia (che dipende dalla forma della sezione).

Invece, il rapporto tra la tensione meccanica e il modulo di Young:

${\displaystyle {\frac {\sigma }{E}}}$

nel caso di un acciaio da costruzione risulta un numero piccolo, intorno al permille, per esempio può essere 200MPa/200GPa = 1/1000.

Effetto del vincolamento

Coefficiente di vincolo per diversi schemi statici della trave

Il profilo dell'inflessione dipende fortemente dalla tipologia dei vincoli. Si definisce per comodità un coefficiente di vincolo, indicato con μ in figura per casi senza forze di taglio. Corrisponde al rapporto tra lunghezza di libera inflessione della trave, e la lunghezza fisica della trave.

I valori del coefficiente per alcuni casi di vincolamento sono:

• • μ = 1 per una trave vincolata con 2 cerniere agli estremi: si veda in figura che la deformata assume la forma di una semplice sinusoide che ha semi-lunghezza d'onda uguale alla lunghezza della trave
  • μ = 2 per una trave vincolata con un solo incastro perfetto (mensola). Si vede in figura che la semi-lunghezza d'onda della deformata è due volte la lunghezza fisica della trave
  • μ = 1/2 per una trave vincolata con 2 incastri perfetti agli estremi
  • μ = 2/3 per una trave vincolata con un incastro perfetto e una cerniera

Da questo coefficiente si calcola la lunghezza di libera inflessione una volta nota la misura della trave, con un semplice prodotto:

${\displaystyle \lambda =\mu \,h}$

Da qui poi si calcola la snellezza massima, conoscendo il raggio di inerzia più piccolo tra quelli delle varie sezioni trasversali della trave.

Caso asta uniforme in presenza di taglio

Descrizione

L'equazione della linea elastica in generale è

${\displaystyle {\frac {d^{2}y(x)}{dx^{2}}}=-{\frac {M(x)}{EJ}}+{\frac {\chi }{GA}}{\frac {dT(x)}{dx}}}$

Sostituendo l'espressione di M e di T si ottiene

${\displaystyle {\frac {d^{2}y(x)}{dx^{2}}}=-{\frac {N}{EJ}}y(x)+{\frac {\chi }{GA}}N{\frac {d^{2}y(x)}{dx^{2}}}}$

Da quest'ultima relazione si ottiene l'equazione differenziale del problema:

${\displaystyle {\frac {d^{2}y(x)}{dx^{2}}}\left(1-N{\frac {\chi }{GA}}\right)=-{\frac {N}{EJ}}y(x)\Rightarrow {\frac {d^{2}y(x)}{dx^{2}}}+{\frac {N}{EJ\left(1-N{\frac {\chi }{GA}}\right)}}y(x)=0\Rightarrow {\frac {d^{2}y(x)}{dx^{2}}}+\alpha ^{2}y(x)=0}$

Per valori pari a ${\displaystyle \alpha ^{2}={\frac {N}{EJ\left(1-N{\frac {\chi }{GA}}\right)}}}$ si ottiene l'equilibrio. La soluzione dell'equazione differenziale è del tipo

${\displaystyle y(x)=A\cos(\alpha x)+B\,\mathrm {sen} (\alpha x)}$

A e B sono costanti che dipendono dalle condizioni al contorno. Dalla condizione ${\displaystyle y(0)=A=0}$, segue che la prima delle due costanti è nulla. Considerando che ${\displaystyle y(L)=B\,\mathrm {sen} (\alpha L)=0}$, che ha due soluzioni possibili:

• se ${\displaystyle \mathrm {sen} (\alpha L)\neq 0}$, deve risultare ${\displaystyle B=0}$. In questo caso la soluzione dell'equazione è ${\displaystyle y(x)\equiv 0}$, ovvero la sola configurazione di equilibrio è quella indeformata.

• se ${\displaystyle \mathrm {sen} (\alpha L)=0}$ allora la condizione al contorno è soddisfatta per qualunque valore di B, pertanto esistono infinite configurazioni equilibrate (equilibrio indifferente).

La condizione ${\displaystyle \mathrm {sen} (\alpha L)=0}$ implica che ${\displaystyle \alpha L=n\pi }$, dove n indica un intero positivo. Ricordando la definizione di ${\displaystyle \alpha }$, si ha che la precedente condizione è soddisfatta se

${\displaystyle {\frac {N_{n}}{EJ\left(1-N_{n}{\frac {\chi }{GA}}\right)}}L^{2}=n^{2}\pi ^{2}}$

Il più piccolo dei valori di ${\displaystyle N_{n}}$ corrisponde al passaggio da una condizione di equilibrio stabile ad una instabile. Tale valore è quello per n = 1, ed è detto il carico critico euleriano dell'asta compressa:

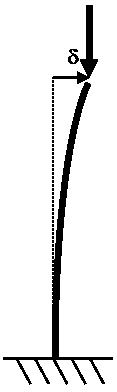
${\displaystyle N_{cr}=\pi ^{2}{\frac {EJ_{\min }}{l_{1}^{2}}}{\frac {1}{\left[1+\pi ^{2}\left({\frac {EJ_{\min }}{l_{1}^{2}}}{\frac {\chi }{GA}}\right)\right]}}}$

Tensione critica

Dal carico critico ne deriva la tensione critica, cioè il valore della tensione raggiunto dall'asta quando ${\displaystyle N=N_{cr}}$

${\displaystyle \sigma _{cr}={\frac {N_{cr}}{A}}=\pi ^{2}{\frac {EJ_{\min }}{l_{1}^{2}A}}{\frac {1}{\left[1+\pi ^{2}\left({\frac {EJ_{\min }}{l_{1}^{2}}}{\frac {\chi }{GA}}\right)\right]}}={\frac {\pi ^{2}{\frac {E}{\lambda ^{2}}}}{1+{\frac {\chi }{GA}}A{\frac {E}{\lambda ^{2}}}\pi ^{2}}}={\frac {\pi ^{2}E}{\lambda ^{2}+{\frac {\chi }{GA}}EA\pi ^{2}}}={\frac {\pi ^{2}E}{\lambda _{id}^{2}}}}$

Caso asta non uniforme in assenza di taglio

Descrizione

Si consideri un'asta la cui rigidezza flessionale non è un valore costante ma variabile lungo l'asse principale, ovvero ${\displaystyle EJ=f(x)}$. Nella pratica dell'ingegneria strutturale la ${\displaystyle f(x)}$ è una funzione che deve rispondere alla seguente condizione: ${\displaystyle f(x)>0}$ con ${\displaystyle 0\leq x\leq L}$ dove ${\displaystyle L}$ rappresenta la lunghezza totale dell'asta. Nell'ingegneria civile la variabilità della rigidezza flessionale dipende esclusivamente dal momento di inerzia, dal momento che è estremamente insolito realizzare elementi strutturali in cui il modulo di Young ${\displaystyle E}$ che rappresenta le proprietà del materiale non sia costante.

La condizione di equilibrio sopra menzionata per il caso di asta omogenea, nel caso presente, diviene

${\displaystyle E\cdot J(x)y''(x)=Ny(x)}$

Posto ${\displaystyle J(x)=J_{0}\cdot h(x)}$, dove ${\displaystyle J_{0}=J(0)}$, le soluzioni dell'equazione differenziale di cui sopra non sono sempre facilmente calcolabili per via del termine ${\displaystyle J(x)}$ presente all'interno di essa. Solo pochi casi sono risolvibili tramite soluzioni analitiche in forma chiusa che di norma sono rappresentate tramite funzioni elementari trigonometriche, tramite funzioni di Bessel o tramite altre funzioni speciali, come ad esempio funzioni ipergeometriche^[1].

Casi reali

In relazione alle aste utilizzate nell'ingegneria civile, la non-uniformità del funzione che esprime il momento di inerzia lungo l'asse principale dell'asta può essere rappresentata tramite la seguente funzione

${\displaystyle h(x)=(1+ax)^{n}}$

dove il parametro ${\displaystyle a}$ rappresenta l'entità della variazione del momento di inerzia, mentre l'esponente ${\displaystyle n}$ dipende dalla forma della sezione. Nella tabella sottostante sono riportati i valori del parametro ${\displaystyle n}$ in relazione alla forma della sezione dell'asta. Non tutte le forme considerate possono essere rappresentante dalla funzione sopra descritta, per cui si ottiene una formulazione approssimata della funzione che descrive la variazione della sezione lungo l'asse principale dell'asta.

Forma della sezione	Parametro ${\displaystyle n}$	Formulazione
Rettangolare, base variabile, altezza costante	1	Esatta
Doppia T, spessore anima trascurabile	2	Approssimata[2]
Doppia T	2.1 a 2.6	Approssimata[2]
Tubolare	3	Approssimata
Rettangolare, base costante, altezza variabile	3	Esatta
Circolare	4	Esatta

Posto

${\displaystyle k^{2}={\frac {N}{EJ_{0}a^{2}}}}$

la soluzione dell'equazione differenziale che regola il problema descritto è

${\displaystyle y(x)={\sqrt {1+ax}}[AJ_{\alpha }(2\alpha k(1+ax)^{\frac {1}{2\alpha }})+BY_{\alpha }(2\alpha k(1+ax)^{\frac {1}{2\alpha }}]}$

dove ${\displaystyle A}$ e ${\displaystyle B}$ sono costanti di integrazione, che richiedono altrettante condizioni al contorno, ${\displaystyle J_{\alpha }}$ e ${\displaystyle Y_{\alpha }}$ corrispondono alle funzioni di Bessel di primo e secondo tipo mentre ${\displaystyle \alpha ={\frac {1}{2-n}}}$.

Quando ${\displaystyle n=2}$ le soluzioni dell'equazione differenziale sono

${\displaystyle y(x)={\sqrt {1+ax}}[Asin({\frac {1}{2}}{\sqrt {|1-4k^{2}|}}\log(1+ax))+Bcos({\frac {1}{2}}{\sqrt {|1-4k^{2}|}}\log(1+ax)]}$

mentre ${\displaystyle n=4}$ le soluzioni dell'equazione differenziale sono

${\displaystyle y(x)=(1+ax)[Asin({\frac {k}{1+ax}})+Bcos({\frac {k}{1+ax}})]}$

Note

1. M. Fabiani e L. Mentrasti, Exact solutions of linear buckling of a class of FGM columns with varying cross-section, in International Journal of Structural Stability and Dynamics, vol. 21, 6 (2021).
2. C. M. Fogel e R. L. Ketter, Elastic strength of tapered columns, in Journal of Structural Division, vol. 88, 5 (1962).

Voci correlate

• Asta composta
• Buckling
• Equazione di Helmholtz
• Instabilità a carico di punta
• Metodo omega
• Numero di Young