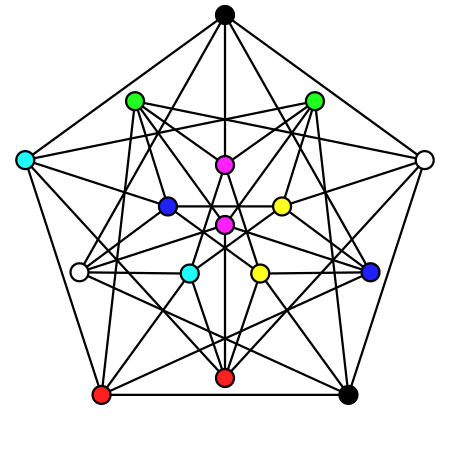
Teljes színezés
|
Read other articles:

Ledi Sayadaw U Ñāṇadhaja လယ်တီဆရာတော် ဦးဉာဏဓဇThe Venerable Ledi SayadawTitleSayadawPersonalBornTet Khaung1 December 1846 (13th waxing of Nadaw 1208 ME)Saingpyin, Dabayin Kingdom of BurmaDied27 June 1923(1923-06-27) (aged 76)Pyinmana, Mandalay Province, British BurmaReligionBuddhismNationalityBurmeseSchoolTheravadaLineageLediEducationAgga Maha Pandita, D.Litt. (Hons.)Dharma namesÑāṇadhaja ဉာဏဓဇOccupationBuddhist monkSenior posti...

Final Fantasy VIII character Fictional character Edea KramerFinal Fantasy characterConcept artwork of Edea Kramer for Final Fantasy VIII, as drawn by Tetsuya Nomura.First gameFinal Fantasy VIII (1999)Created byTetsuya Nomura Edea Kramer (Japanese: イデア・クレイマー, Hepburn: Idea Kureimā) is a character and a major antagonist in Final Fantasy VIII. Protagonist Squall is sent to assassinate her, though it is later discovered that the Sorceress Ultimecia had Edea under mind control. ...

Menara PriceMenara Price, Bartlesville, OklahomaInformasi umumJenisMultifungsiLokasi510 Dewey AvenueBartlesville, Oklahoma, A.S.Mulai dibangun1952Rampung1956TinggiMenara antena221 ft (67 m)Data teknisJumlah lantai19Luas lantai42.000 square feet (3.900 m2)Lift4Desain dan konstruksiArsitekFrank Lloyd WrightKontraktor utamaHaskell CaldwellMenara PriceDaftar Kawasan Bersejarah Nasional di ASU.S. National Historic LandmarkFrank Lloyd Wright, Price TowerLetak:Bartlesville, OklahomaKo...

Pour les articles homonymes, voir Bataille de Kidal. Bataille de Kidal Vue en 2005, de l'entrée de Kidal. Informations générales Date 26 - 30 mars 2012 Lieu Kidal Issue Victoire des rebelles Belligérants Mali Ansar Dine MNLA AQMI Commandants El Hadj Ag Gamou Iyad Ag Ghali Ba Ag Moussa Assalat Ag Habi Forces en présence 500 hommes[1] inconnues Pertes inconnues~ 50 à 100 prisonniers inconnues Guerre du MaliBatailles Batailles de la guerre du Mali Rébellion touarègue de 2012 Ménaka (1re...

Fumizuki pada bulan Juli 1926 Sejarah Kekaisaran Jepang Nama FumizukiAsal nama JuliPembangun Fujinagata Shipyards, OsakaNomor galangan Perusak No. 29Pasang lunas 20 Oktober 1924Diluncurkan 16 Februari 1925Selesai 3 Juli 1926Ganti nama Fumizuki, 1 Agustus 1928[1]Dicoret 31 Maret 1944Identifikasi Nomor lambung: 29Nasib Tenggelam oleh pesawat Amerika pada 18 Februari 1944 Ciri-ciri umum Kelas dan jenis Kapal perusak kelas-MutsukiBerat benaman 1.336 t (1.315 ton panjang) (normal) 1.8...

كوليرا شخص مصاب بجفاف حاد نتيجة اصابته بالكوليراشخص مصاب بجفاف حاد نتيجة اصابته بالكوليرا معلومات عامة الاختصاص أمراض معدية، وطب الطوارئ من أنواع أمراض معدية معوية، وأمراض تنقلها المياه، ومرض بكتيري معدي أولي [لغات أخرى]، ومرض أنثروبونيوتيك &...

Nadiya SavchenkoНадія Савченко People's Deputy of Ukraine8th convocationMasa jabatan27 November 2014 – 24 Juli 2019Daerah pemilihanBatkivshchyna, No.1[1] Informasi pribadiLahirNadiya Viktorivna Savchenko11 Mei 1981 (umur 42)Kyiv, Ukrainian SSR, Uni Soviet (sekarang Ukraina)Partai politikSocial and Political Platform of Nadiya Savchenko (sejak 2017)Afiliasi politiklainnyaBatkivshchyna (2014–2016)Penghargaan sipil Hero of Ukraine Order For CourageKarier mi...

Telecommunications tower in Shanghai, China This article is about the building in Shanghai. For the building in Manila, see Pearl of the Orient Tower. Oriental Pearl Radio & TV Tower东方明珠广播电视塔The Oriental Pearl Tower in December 2014General informationTypeCommunication, hotel, observation, restaurantLocationShanghaiCoordinates32°14′30″N 120°29′41″E / 32.241669°N 120.494719°E / 32.241669; 120.494719Construction startedJuly 30, ...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Colin James and the Little Big Band II – news · newspapers · books · scholar · JSTOR (June 2017) 1999 studio album by Colin JamesColin James and the Little Big Band IIStudio album by Colin JamesReleased26 January 1999Recorded1998GenreJump blue...

American educator and politician Nick MelvoinMember of the Los Angeles Unified School District Board of Educationfrom the 4th districtIncumbentAssumed office July 6, 2017Preceded bySteve ZimmerVice President of the Los Angeles Unified School District Board of EducationIn officeJuly 6, 2017 – January 17, 2023PresidentKelly GonezPreceded bySteve ZimmerSucceeded byScott Schmerelson Personal detailsBornNicholas James Melvoin1985 (age 37–38)Los Angeles, California, U.S.Po...

Ban Pong redirects here. For the district capital, see Ban Pong, Ratchaburi. For other similarly named places, see Ban Pong (disambiguation). District in Ratchaburi, ThailandBan Pong บ้านโป่งDistrictBan Pong Municipal OfficeDistrict location in Ratchaburi provinceCoordinates: 13°48′51″N 99°52′16″E / 13.81417°N 99.87111°E / 13.81417; 99.87111CountryThailandProvinceRatchaburiArea • Total366.6 km2 (141.5 sq mi)Populat...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2021) رأب الوعاء الرئوي بالبالون تعديل مصدري - تعديل رأب الوعاء الرئوي بالبالون هو إجراء جراحي طفيف التوغل لعلاج ارتفاع ضغط الدم الرئوي الانصمامي الخثاري المز...

Extinct genus of turtles LeyvachelysTemporal range: Late Aptian-Early Albian~119-113 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Clade: Pantestudines Clade: Testudinata Family: †Sandownidae Genus: †LeyvachelysCadena, 2015 Species: †Leyvachelys cipadi Binomial name †Leyvachelys cipadiCadena, 2015 Paleogeography of Northern South America120 Ma, by Ron Blakey Synonyms Glenrosechelys...

Building in Chicago North PierLocationChicago, Illinois, United StatesCoordinates41°53′26.8″N 87°36′58.7″W / 41.890778°N 87.616306°W / 41.890778; -87.616306Address435 E. Illinois St., Chicago, IL 60611Opening date1990Closing date2013DeveloperBroadacre ManagementArchitectChristian Eckstorm (Pugh Terminal), Booth Hansen (North Pier), FitzGerald Associates Architects (Lofts at River East)Total retail floor area200,000 sq ft (18,581 m2)No. of flo...

Sampul novel Chunhyangjeon yang diterbitkan pada awal abad ke-20. Chunhyangjeon atau Kisah Chunhyang (춘향전;春香傳) adalah sebuah novel klasik mengenai romansa percintaan sepasang kekasih di Korea pada masa Dinasti Joseon (1392-1910).[1][2] Sejarah Chunhyangjeon ditulis pada akhir periode Dinasti Joseon (abad ke-17 sampai ke-18).[1] Cerita novel ini didasarkan pada narasi pansori (opera tradisional) yang penulisnya tak diketahui, karena dipelajari dengan cara di...

Region to the east of Central America This article is about the group of islands. For the body of water surrounding them, see Caribbean Sea. For the indigenous inhabitants of the Caribbean or people of Caribbean descent, see Caribbean people. For other uses, see Caribbean (disambiguation). CaribbeanArea239,681 km2 (92,541 sq mi)Population44,182,048[1][2]Population density151.5/km2 (392/sq mi)Ethnic groupsAfro-Caribbean, Latino or Hispanic, (Spanish, Portugu...

British publishing company This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Titan Publishing Group – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when to remove this template message) Titan Publishing GroupParent companyTitan EntertainmentFounded1981FounderNick LandauVivian CheungCoun...

Iranian-American professor and historian (1943–2021) George A. BournoutianBorn(1943-09-25)September 25, 1943Isfahan, IranDiedAugust 22, 2021(2021-08-22) (aged 77)New Jersey, U.S.OccupationProfessor George A. Bournoutian (Armenian: Ջորջ Բուռնութեան;[1] Persian: جورج بورنوتیان, 25 September 1943 – 22 August 2021) was an Iranian-American professor, historian, and author of Armenian descent.[2] He was a professor of history and the ...

Condado de Suwannee Condado Ubicación en el estado de FloridaCoordenadas 30°11′N 82°59′O / 30.19, -82.99Sede de condado Live OakEntidad Condado • País Estados Unidos • Estado FloridaEventos históricos • Fundación 21 de diciembre de 1858Superficie • Total 1792 km² • Agua 11 km² (4 mi²) km²Población (2000) • Total 34 844 hab. • Densidad 24,26 hab/km² Sitio web o...

16th Special Operations Squadron AC-130A Hercules of the 16th Special Operations Squadron [note 1]Active1942–1944; 1944–1945; 1968–presentCountry United StatesBranch United States Air ForceRoleSpecial OperationsPart ofAir Force Special Operations CommandGarrison/HQCannon Air Force BaseMotto(s)SpectreDecorations Distinguished Unit Citation Presidential Unit Citation Gallant Unit Citation Air Force Outstanding Unit Award with Combat V Device Republic of Vietnam Gall...