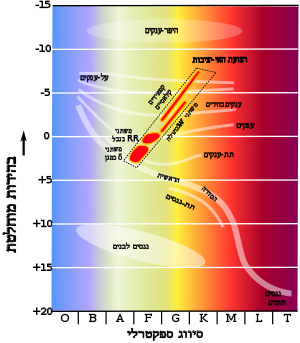
משתנה קפאידי
|
Read other articles:

Bupati LebakSunda: ᮘᮥᮕ᮪ᮒᮤ ᮜᮨᮘᮊ᮪PetahanaIti Octavia Jayabayasejak 15 Januari 2014KediamanPendopo Kabupaten LebakMasa jabatan5 tahun dan dapat dipilih kembali untuk satu kali masa jabatanDibentuk1919; 104 tahun lalu (1919)Pejabat pertamaPangeran SendjajaSitus webSitus web resmi Halaman ini berisi tentang daftar politisi yang terpilih dalam pemilihan umum dan dilantik sebagai Bupati Lebak. Sejauh ini, terdapat 27 orang yang telah menduduki jabatan ini. Berikut mer...

Religion in Sri Lanka (2011)[1] Phật giáo (70.19%) Ấn Độ giáo (12.6%) Hồi giáo (9.7%) Kitô giáo (7.4%) Không tôn giáo (0.8%) Bản đồ phân bố tôn giáo tại Sri Lanka, D.S. Divisions, 2011. Người dân Sri Lanka là các tín đồ của nhiều tôn giáo khác nhau. Theo điều tra dân số năm 2011, 70.19% người dân Sri Lanka theo Phật giáo Thượng tọa bộ, 12....

Maastricht: kapel van Maria, Sterre der Zee O reinste der schepselen, ook wel – naar het refrein – O Sterre der Zee of Lied van de Sterre der Zee genoemd, is een aan Maria, Sterre der Zee gewijde hymne in de Rooms-Katholieke Kerk. Het lied is met name bij katholieken in Maastricht en Limburg populair; in Maastricht wordt het nog steeds veelvuldig gezongen tijdens processies en tijdens missen in de Onze-Lieve-Vrouwebasiliek, waar zich de kapel van de Sterre der Zee bevindt. Geschiedenis La...

Januário da Cunha Barbosa Januário da Cunha Barbosa Nascimento 10 de julho de 1780Rio de Janeiro Morte 22 de fevereiro de 1846 Cidadania Brasil Ocupação jornalista, escritor, poeta, bibliotecário Empregador(a) Biblioteca Nacional do Brasil [edite no Wikidata] Ouça o artigo (info)noicon Este áudio foi criado a partir da revisão datada de 22 de novembro de 2017 e pode não refletir mudanças posteriores ao artigo (ajuda). Mais artigos audíveis Januário da Cunha Barbosa (S. A. Siss...

Patung marmer Kibele dari abad ke-1 SM Formia, Latium. Kibele (/[invalid input: 'icon']ˈkɪbəliː/ atau [ˈsɪb.əl.i]; bahasa Frigia: Matar Kubileya/Kubeleya Bunda Kubeleyan, kemungkinan Bunda Gunung; bahasa Yunani: Κυβέλη Kybele, Κυβήβη Kybebe, Κύβελις Kybelis), adalah Ibu Bumi dalam kepercayaan Frigia. Seperti juga Gaia dari Yunani dan Rea dari Minoa, Kibele merupakan perwujuan bumi yang subur. Kibele juga adalah dewi gua dan gunung, dinding dan benteng, alam, hewa...

Yonah Shimmel's Knish Bakery specializes in knishes. This is a list of notable kosher restaurants. A kosher restaurant is an establishment that serves food that complies with Jewish dietary laws (kashrut). These businesses, which also include diners, cafés, pizzerias, fast food, and cafeterias, and are frequently in listings together with kosher bakeries, butchers, caterers, and other similar places, differ from kosher-style establishments, which offer traditionally Jewish foods made from no...

Not to be confused with Atlantic Beach, New York. Hamlet and census-designated place in New York, United StatesEast Atlantic Beach, New YorkHamlet and census-designated placeNickname: Snob HillLocation in Nassau County and the state of New York.East Atlantic Beach, New YorkLocation within the state of New YorkCoordinates: 40°35′17″N 73°42′21″W / 40.58806°N 73.70583°W / 40.58806; -73.70583CountryUnited StatesStateNew YorkCountyNassauArea[1] ...

Spanish actress and singer In this Spanish name, the first or paternal surname is Mérida and the second or maternal family name is Rojas. Victoria AbrilAbril at the 2013 Cannes Film FestivalBornVictoria Mérida Rojas (1959-07-04) 4 July 1959 (age 64)Malaga, SpainOccupation(s)Actress and singerYears active1974–presentSpouses Pierre Edelman Gustavo Laube PartnerGérard de BattistaAwardsSilver Bear for Best Actress1991 Amantes Goya Award for Best Actress1995 Nobody Will Spea...

DelilahDelilah performing in late 2011Background informationBirth namePaloma Ayana StoeckerAlso known asDelilahBorn (1990-09-23) 23 September 1990 (age 33)Paris, FranceOriginCamden, London, EnglandGenres Pop electronica trip hop PBR&B ambient soul Occupation(s)Singer-songwriterInstrument(s)Vocals, pianoYears active2007–presentLabelsAtlantic, Warner Music GroupWebsitedelilahofficial.comMusical artist Paloma Ayana Stoecker (born 23 September 1990), who records under the name Delilah,...

Railway station in Miyoshi, Hiroshima Prefecture, Japan Yatsugi Station八次駅Yatsugi Station, March 2018General informationLocation140 Minamihatajikimachi, Miyoshi-shi, Hiroshima-ken 728-0017JapanCoordinates34°48′8.55″N 132°52′44.08″E / 34.8023750°N 132.8789111°E / 34.8023750; 132.8789111Owned by West Japan Railway CompanyOperated by West Japan Railway CompanyLine(s) P Geibi Line Z Geibi Line Distance88.0 km (54.7 mi) from Bitchū-KōjiroPlatfo...

Mexican politician In this Spanish name, the first or paternal surname is Aguilar and the second or maternal family name is Gil. Lilia Aguilar GilBorn (1977-08-17) 17 August 1977 (age 46)Ojinaga, Chihuahua, MexicoOccupationDeputyPolitical party PT Lilia Aguilar Gil (born 17 August 1977) is a Mexican politician affiliated with the PT. She currently serves as Deputy of the LXII Legislature of the Mexican Congress representing Chihuahua.[1] References ^ Perfil del legislador...

1904 British documentary film This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: A Day in the Hayfields – news · newspapers · books · scholar · JSTOR (March 2022) A Day in the HayfieldsScreenshot: Hay-makingDirected byCecil M. HepworthProductioncompanyHepworthRelease date 1904 (1904) Running time...

Ethnic group native to Flanders, Belgium Flemings redirects here. For other uses, see Flemings (disambiguation). FlemingsVlamingenFlag of Flanders, the symbol of the Flemish people.Flemish Community in Belgium and EuropeTotal populationc. 7 million(2011 estimate)Regions with significant populations Belgium (Flanders)6,450,765[1] United StatesIndeterminable[a](352,630 Belgians)[2] France187,750[3] Canada13,840–176,615[b][4] South Afric...

Liga Endesa 2018-19Liga Liga EndesaNº de equipos 18Partidos jugados 306 (Temporada regular)19 (Playoffs)TV Cuadro de honorCampeón Real MadridSubcampeón FC Barcelona LassaSemifinalistas Valencia Basket Tecnyconta ZaragozaCabeza(s) de serie Real MadridRelevo de plazas Ascenso(s) Real Betis Energía Plus (1º) y RETAbet Bilbao Basket (2º) Descenso(s) Delteco GBC (17º) y Cafés Candelas Breogán (18º)GalardonesMVP Nicolás LaprovittolaMVP finales Facundo CampazzoLíderes estadísticosValora...

Cloth used to cover a table This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tablecloth – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Traditional Romanian tablecloth made in Maramureş Cover for Square Table, Qing dynasty, Qianlong period, 1...

Israeli politician and lawyer Yulia MalinovskyYulia MalinovskyFaction represented in the Knesset2016–2018Yisrael Beiteinu2019–Yisrael Beiteinu Personal detailsBorn (1975-09-05) 5 September 1975 (age 48)Voroshilovgrad, Soviet UnionEducationEast Ukrainian Volodymyr Dahl National University Yulia Malinovsky (Hebrew: יוּלְיָה מַלִינוֹבְסְקִי, Russian: Юлия Малиновская, Yuliya Malinovskaya; born 5 September 1975) is an Israeli politician, lawye...

Annual budget of the Republic of India () Union budget of IndiaGovernmentGovernment of IndiaWebsitewww.indiabudget.gov.in‹ February 2023February 2024 › The Union Budget of India, also referred to as the Annual Financial Statement in Article 112 of the Constitution of India,[1] is the annual budget of the Republic of India set by Ministry of Finance for the following financial year, with the revenues to be gathered by Department of Revenue to identify planned govern...

MONSTER ジャンル 青年漫画・サスペンス 漫画 作者 浦沢直樹 出版社 小学館 その他の出版社 Viz MediaKanaEgmont Manga & AnimePlanet MangaPlaneta DeAgostiniConrad Editora鶴山文化社東立出版社Grupo Editorial VidNation EdutainmentM&C Comics 掲載誌 ビッグコミックオリジナル レーベル ビッグコミックス 発表期間 1994年12月 - 2001年12月 巻数 単行本:全18巻完全版:全9巻 アニメ 原作 浦沢直樹 監督 �...

此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2015年8月19日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 爱彼迎AirbnbAirbnb驻加拿大多伦多办公室公司類型上市公司股票代號NASDAQ:ABNB成立2008年創辦人布萊恩·切斯基、喬·傑比亞、內森·布萊卡斯亞克 代表人物布萊恩·切斯基(執行長)喬·傑比亞(CPO)Nathan Blecharczyk(CTO)總部 美國�...

第4航空群 第4航空群ロゴマーク創設 1962年(昭和37年)9月1日所属政体 日本所属組織 海上自衛隊部隊編制単位 群兵種/任務/特性 対艦・対潜航空部隊所在地 神奈川県 綾瀬市上級単位 航空集団テンプレートを表示 第4航空群(だいよんこうくうぐん、英称:Fleet Air Wing 4)とは、海上自衛隊の航空集団隷下の航空部隊(航空群)の一つであり、厚木航空基地(神奈川県綾瀬�...