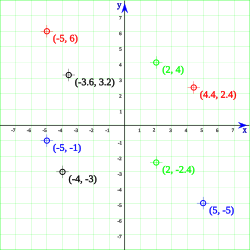
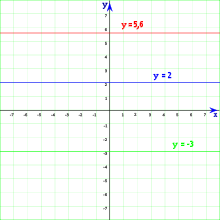
Xeometría analítica
|
Read other articles:

San Bernardo Central Datos generalesNombre Club Deportivo San Bernardo CentralFundación 1956Desaparición 14 de diciembre de 1994InstalacionesEstadio MaestranzaUbicación San Bernardo, ChileUniforme Titular [editar datos en Wikidata] El Club Deportivo San Bernardo Central[1] fue un club de fútbol de Chile, con sede en San Bernardo, asociado a la Maestranza San Bernardo de los Ferrocarriles del Estado. Fue fundado en 1956 y jugaba de local en el Estadio Maestranza. Historia ...

Sports season2006 Sun Belt Conference football seasonLeagueNCAA Division I FBS (Football Bowl Subdivision)SportfootballDurationAugust 28, 2006through January 6, 2007Number of teams8TV partner(s)ESPN2007 NFL DraftTop draft pickBrannon CondrenPicked byIndianapolis Colts, 131st overallRegular seasonChampionTroySeason MVPOmar HaugabookFootball seasons← 20052007 → 2006 Sun Belt Conference football standings vte Conf Overall Team W L W L Troy ...

Способом самоубийства (суицида) называют любые действия, с помощью которых человек совершает самоубийство, намеренно уходя из жизни. Самоубийство не всегда завершается смертью, и неудавшаяся попытка самоубийства может привести к серьезным физическим травмам, долгосро�...

العلاقات السلوفاكية الغامبية سلوفاكيا غامبيا سلوفاكيا غامبيا تعديل مصدري - تعديل العلاقات السلوفاكية الغامبية هي العلاقات الثنائية التي تجمع بين سلوفاكيا وغامبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ال�...

主体思想塔两侧建筑物上的“一心团结”(일심 단결)标语 朝鲜民主主义人民共和国 朝鲜民主主义人民共和国政府与政治系列条目 朝鲜劳动党 主體朝鮮永遠的首領:金日成、金正日 金日成家族 全国代表大会(八大) 中央委员会(第八届) 总书记:金正恩 中央政治局 / 常务委员 中央书记局 中央军事委员会 委员长:金正恩 中央检阅委员会 委员长:洪仁範 政府 国家宪政...

Archaeological museum in Delphi, GreeceDelphi Archaeological MuseumΑρχαιολογικό Μουσείο ΔελφώνDelphi Archaeological MuseumLocation within GreeceEstablished1903 (1903)LocationΤ.Κ. 33054, Delphi, GreeceCoordinates38°28′48″N 22°30′00″E / 38.4801275°N 22.4999303°E / 38.4801275; 22.4999303TypeArchaeological museumCollectionsGreek antiquitiesVisitors137,550 (2009)[1]OwnerGreek Ministry of Culture (10th ephorate of preh...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (ديسمبر 2022) التقنين الدولي للوصف الببليوجرافي أو اختصاراً تدوب وهو مجموعة من التقنينات ا�...

Hansraj RaghuwanshiBorn18 July 1992 (1992-07-18) (age 31)Bilaspur, Himachal Pradesh, IndiaOccupation(s)Singer, Composer and WriterYears active2016–presentMusical careerGenres Devotional film Instrument(s)VocalsLabels T-Series Websitehansrajraghuwanshi.inYouTube informationChannel Hansraj Raghuwanshi Years active2016–presentGenres Devotional music Subscribers11.2 million[1]Total views2.13 billion[1]Last updated: 21 October 2023 Musical artist Hansra...

الإسلام في فنلندا هم أقلية مسلمة تعيش في فنلندا.جزء من سلسلة مقالات حولالإسلام حسب البلد الإسلام في إفريقيا أنغولا بنين بوتسوانا بوركينا فاسو بوروندي الكاميرون الرأس الأخضر أفريقيا الوسطى نشاد الجزائر جزر القمر الكونغو الديمقراطية الكونغو ساحل العاج جيبوتي مصر غينيا ال�...

ZoomTheatrical release posterSutradara Peter Hewitt Produser Suzanne Todd Jennifer Todd Todd Garner Trevor Engelson Ditulis oleh Adam Rifkin David Berenbaum SkenarioAdam Rifkin, David BerenbaumCeritaAdam RifkinBerdasarkanAmazing Adventures from Zoom's Academyoleh Jason LethcoePemeran Tim Allen Courteney Cox Chevy Chase Spencer Breslin Rip Torn NaratorCourteney CoxPenata musikChristophe BeckSinematograferDavid TattersallPenyuntingLawrence JordanPerusahaanproduksi Columbia Pictures Revolu...

Quema de los ídolos y documentos mayas por Fray Diego de Landa. Mural del pintor mexicano Fernando Castro Pacheco. La Inquisición española desarrolló su actividad en los territorios españoles de América a través de tres tribunales: los de Lima y México fundados en 1569, y el de Cartagena de Indias, fundado en 1610. En el resto de las colonias españolas americanas también actuaba, por medio de un comisario y el subsiguiente sistema de notarios y familiares (delatores oficiales), suje...

Species of butterfly Spotted mystic Lethe tristigmata in Lepidoptera Indica Scientific classification Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Nymphalidae Genus: Lethe Species: L. tristigmata Binomial name Lethe tristigmataElwes, 1887[1] Lethe tristigmata, the spotted mystic, is a species of Satyrinae butterfly found in the Indomalayan realm (Sikkim, Nepal) .[2][3] In 2015, it was also recorded from Neora Valley National Park...

British artist (1769–1849) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ellen Sharples – news · newspapers · books · scholar · JSTOR (November 2014) (Learn how and when to remove this template message) Ellen SharplesPortrait of Sharples, painted by her daughter, Rolinda, c. 1814.BornEllen Wallace(...

Bagian dari seri politik tentangAnarkisme Aliran pemikiran Kulit hitam Kapitalis Kristen Kolektif Komunis Egois Eksistensialis Feminis Hijau Individualis Pemberontakan Kiri Pasar sayap kiri Magonis Mutualis Naturis Pasifis Filosofis Platformis Pasca-anarkis Pascakolonial Pascakiri Primitivis Queer Sosial Sindikalis Sintesis Vegan Tanpa ajektiva TeoriPraktik Anarki Anarchist Black Cross Anasionalisme Anti-otoritarianisme Antimilitarisme Kelompok afinitas Blok hitam Masyarakat tanpa kelas Perju...

Juan López de Zárate I Obispo de Antequera, OaxacaPredecesor NingunoSucesor Bernardo de Albuquerque O.P.Información religiosaOrdenación episcopal 8 de abril de 1537por Juan de Zumárraga O.F.M.Información personalNombre Juan López de ZárateNacimiento 24 de junio de 1490 en Oviedo, EspañaFallecimiento 10 de septiembre de 1555 en Ciudad de México (65 años)[editar datos en Wikidata] Juan López de Zárate (Oviedo, España, 24 de junio de 1490 - Ciudad de México, 10 de s...

Concurrent Haskell extends[1] Haskell 98 with explicit concurrency. Its two main underlying concepts are: A primitive type MVar α implementing a bounded/single-place asynchronous channel, which is either empty or holds a value of type α. The ability to spawn a concurrent thread via the forkIO primitive. Built atop this is a collection of useful concurrency and synchronisation abstractions[2] such as unbounded channels, semaphores and sample variables. Haskell threads have ve...

Winter capital of Uttarakhand, India Metropolis in Uttarakhand, IndiaDehradun Dehra DoonMetropolisDoon ValleyRobber's CavesTapkeshwar TempleIndian Military AcademyKhalanga War MemorialThe Doon SchoolDehradun International Cricket StadiumForest Research InstituteNickname: DoonDehradunShow map of UttarakhandDehradunShow map of IndiaCoordinates: 30°20′42″N 78°01′44″E / 30.345°N 78.029°E / 30.345; 78.029Country IndiaStateUttarakhandDistrictDehradunFou...

Vice-presidential election in India 1987 Indian vice presidential election ← 1984 7 September 1987 1992 → Nominee Shankar Dayal Sharma Party INC Home state Madhya Pradesh Electoral vote Unopposed Vice President before election Vacant, last held by R. Venkataraman INC Elected Vice President Shankar Dayal Sharma INC The 1987 Indian vice presidential election was held in mid-1987 to elect the vice president of India, after the incumbent R. Venkataraman's re...

此條目介紹的是馬來西亞的2020年宏願。关于其他的2020年宏願,请见「2020年宏願 (消歧義)」。 以下条目属于马哈迪·莫哈末系列的一部分 马来西亚首相 槟威大桥 布城 赛城 吉隆坡塔 雙峰塔 吉隆坡国际机场 南北大道 馬來西亞國際伊斯蘭大學 牙直利(英语:Guthrie (company)) MEASAT卫星系统(英语:MEASAT Satellite Systems) 雪邦国际赛道 寶騰(前称普腾) 宝腾赛加(英语�...

Eastern Zhejiang CanalView of the canal from Taiping Bridge, ShaoxingSpecificationsLength239 miles (385 km)HistoryConstruction beganSpring and Autumn PeriodDate restored29 December 2007GeographyStart pointXixing, Binjiang District, HangzhouEnd pointYong River, Zhenhai District, NingboConnects toQiantang River, East China Sea Eastern Zhejiang CanalTraditional Chinese浙東運河Simplified Chinese浙东运河TranscriptionsStandard MandarinHanyu PinyinZhèdōng YùnhéWade–GilesChe-t...