Cubo de Rubik
|
Read other articles:

中华人民共和国学生(青年)运动会China National Student (Youth) Games簡稱学青会首屆賽事2023年每隔4年舉辦對象中国中学生、大学生、青年 中华人民共和国学生(青年)运动会(英語:Student (Youth) Games of the People's Republic of China),简称学青会,由原中华人民共和国青年运动会和中华人民共和国学生运动会合并而成,每4年举办一次,和全运会间隔2年交替举行[1]。首届学青会...

1971 film King LearFilm posterDirected byPeter BrookWritten byPeter BrookWilliam ShakespeareProduced byMichael BirkettMogens Skot-HansenStarringPaul ScofieldCinematographyHenning KristiansenEdited byKasper SchybergProductioncompaniesFilmwaysRoyal Shakespeare CompanyDistributed byColumbia PicturesRelease date 4 February 1971 (1971-02-04) Running time137 minutesCountryUnited KingdomLanguageEnglish King Lear is a 1971 British film adaptation of the Shakespeare play directed by Pet...

جُزء من سلسلة مقالات حولالرأسمالية مفاهيم عمل تجاري دورة أعمال أصحاب أعمال رأس مال تراكم رأس المال سوق رأس المال شركة مؤسسة تجارية منافسة تدخل اقتصادي ليبرالية اقتصادية فائض اقتصادي ريادة أعمال رأس مال وهمي سوق مالية Free price system سوق حر Goods and services مستثمر اليد الخفية Liberalization �...

Логотип організації «Медична Система Національної Катастрофи» «Націона́льно-меди́чна систе́ма катастро́ф», НМСК, «Медична Система Національної Катастрофи», МСНК (англ. National Disaster Medical System, NDMS) — це частина Департаменту охорони здоров'я та соціальних служб США, відпов�...

Football tournament season 1969 National Challenge CupDewar Challenge CupTournament detailsCountry USADates5 January-29 June 1969Defending championsGreek American AAFinal positionsChampionsGreek American AA (3rd title)Runner-upMontabello ArmeniansSemifinalistsHansaHellenic1970 CONCACAF Champions' CupGreek American AA← 19681970 → The 1969 National Challenge Cup was the 56th edition of the United States Soccer Football Association's annual open soccer championship. Th...

Members of Parliament from Punjab, India There are total 20 members of Parliament from Punjab: 13 in Lok Sabha and 7 in Rajya Sabha. 13 Lok Sabha members are elected from 13 single member constituencies by First past the post voting system.[1] Last election was held on all seats in 2019. 7 Rajya Sabha members are elected by Single transferable vote system by members of Punjab Legislative Assembly. However the elections held at different times and not at same time on all seats. Last el...

オリンピックのボスニア・ヘルツェゴビナ選手団 ボスニア・ヘルツェゴビナの国旗 IOCコード: BIH NOC: ボスニア・ヘルツェゴビナオリンピック委員会公式サイト 2016年リオデジャネイロオリンピック 人員: 選手 11人 旗手: アメル・トゥカ メダル国別順位: – 位 金0 銀0 銅0 計0 夏季オリンピックボスニア・ヘルツェゴビナ選手団 1992 • 1996 • 2000 • 200...
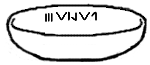
Symbols found upon Vinča culture artifacts This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vinča symbols – news · newspapers · books · scholar · JSTOR (February 2012) (Learn how and when to remove this template message) A modern drawing of a clay vessel unearthed in Vinča, found at depth of 8.5 meters. Th...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Kalpurnia – berita · surat kabar · buku · cendekiawan · JSTOR Calpurnia dari Promptuarii Iconum Insigniorum abad ke-16 Calpurnia adalah istri ketiga dan terakhir dari Julius Caesar. Lahir pada 75 SM, ia ...

Five-member governing body of Los Angeles County, California County of Los Angeles Board of SupervisorsTypeTypeUnicameral board of Los Angeles CountyTerm limits3 terms (12 years)HistoryFounded1852 (1852)Preceded byCourt of SessionsLeadershipCounty ChairJanice Hahn since 2022 County Chair Pro TemLindsey Horvath since 2022 Supervisor, First DistrictHilda Solis since 2014 Supervisor, Second DistrictHolly Mitchell since 2020 Supervisor, Third DistrictLindsey Horvath since 2022 Superviso...

Biological process occurring in plants Diagram illustrating the process of pollination Female carpenter bee with pollen collected from a night-blooming cereusPollination is the transfer of pollen from an anther of a plant to the stigma of a plant, later enabling fertilisation and the production of seeds, most often by an animal or by wind.[1] Pollinating agents can be animals such as insects, for example beetles; birds, butterflies, and bats; water; wind; and even plants themselves. P...
International cycling contest 2021–22 UCI Track Cycling seasonDetailsDates28 October 2021 –LocationWorld← 2020–21 2022–23 → The 2021–22 UCI Track Cycling season is the seventeenth season of the UCI Track Cycling Season. The 2021–22 season began on 28 October 2021 with the Indonesian Track National Championships and will end in October 2022 with 2022 UCI Track Cycling World Championships. It is organised by the Union Cycliste Internationale. Events 2021 Event ...

System to specify locations on Earth For broader coverage of this topic, see Spatial reference system. Geodesy Fundamentals Geodesy Geodynamics Geomatics History Concepts Geographical distance Geoid Figure of the Earth (radius and circumference) Geodetic coordinates Geodetic datum Geodesic Horizontal position representation Latitude / Longitude Map projection Reference ellipsoid Satellite geodesy Spatial reference system Spatial relations Vertical positions Technologies Global Nav. S...

Political family in Sri Lanka Rajapaksa familyCurrent regionHambantotaPlace of originMedamulana, WeeraketiyaMembersD. M. RajapaksaD. A. RajapaksaGeorge RajapaksaLakshman RajapaksaChamal RajapaksaMahinda RajapaksaGotabhaya RajapaksaBasil RajapaksaNirupama RajapaksaShasheendra RajapaksaNamal RajapaksaNipuna Ranawaka The Rajapaksa family (Sinhala: රාජපක්ෂ, romanized: Rājapakṣa) is a Sri Lankan family that is prominent in politics. It was one of Sri Lanka's most powerful fam...

2017 South Korean television series Ms. PerfectGenreMysteryComedyWritten byHong Seok-kuDirected byYoon Kyung-ahStarringKo So-youngYoon Sang-hyunCho Yeo-jeongSung JoonCountry of originSouth KoreaOriginal languageKoreanNo. of episodes20ProductionExecutive producersLee Gun-junLee Jae-gilProducersJun Jae-yeonChoi Jun-hoRunning time60 minutesProduction companiesMs. Perfect SPCKBS MediaOriginal releaseNetworkKBS2ReleaseFebruary 27 (2017-02-27) –May 2, 2017 (2017-05-02) Ms. Perfect ...

Hospital in East Cowes, United KingdomFrank James HospitalThe hospital when it was known as the Frank James Cottage HospitalShown in Isle of WightGeographyLocationEast Cowes, United KingdomCoordinates50°45′19″N 1°17′09″W / 50.75531°N 1.285726°W / 50.75531; -1.285726OrganisationCare systemPublic NHSFundingPublic hospitalTypeHome for seamenServicesEmergency departmentNo Accident & EmergencyHistoryOpened1903Closed2002LinksListsHospitals in the United Kingd...

Condition in which an individual cannot feel pleasure from an orgasm This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Sexual anhedonia – news · newspapers · books · scholar · JSTOR (April 2013) Sexual anhedonia, also known as pleasure dissociative orgasmic disorder, is a condition in which an indivi...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Ancestors – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this template message) 1983 studio album by Tim Berne SextetThe AncestorsStudio album by Tim Berne SextetReleased1983RecordedFebruary 19th 1983GenreAvan...

Sporting event delegationBulgaria at theOlympicsIOC codeBULNOCBulgarian Olympic CommitteeWebsitewww.bgolympic.org (in Bulgarian and English)Medals Gold 52 Silver 89 Bronze 83 Total 224 Summer appearances18961900–1920192419281932193619481952195619601964196819721976198019841988199219962000200420082012201620202024Winter appearances193619481952195619601964196819721976198019841988199219941998200220062010201420182022 This is a list of flag bearers who have represented Bulgaria at the Olympic...

1995 video gameWireheadCover artDeveloper(s)The Code MonkeysPublisher(s)Sega MGM InteractivePlatform(s)Sega CDReleaseSeptember 1995Genre(s)AdventureMode(s)Single-player Wirehead is an interactive movie developed by The Code Monkeys for the Sega CD, and published by Sega and MGM Interactive in 1995. Wirehead was one of the last games released for the Sega CD, and one of the platform's most ambitious full-motion video productions. A Sega 32X CD port was planned, but was canceled. Gameplay Ned H...























