Réunion disjointe
|
Read other articles:

Sala de Conciertos Cemal Reşit Rey Cemal Reşit Rey Konser Salonu Vista del espacioLocalizaciónPaís TurquíaLocalidad EstambulCoordenadas 41°02′53″N 28°59′24″E / 41.04805556, 28.99Información generalTipo Sala de conciertosApertura 1989CaracterísticasAforo 860 espectadores[editar datos en Wikidata] La Sala de Conciertos Cemal Reşit Rey[1] (en turco: Cemal Reşit Rey Konser Salonu) es una sala de conciertos ubicada en el barrio Harbiye de E...

У Вікіпедії є статті про інші значення цього терміна: Діафрагма. Діафрагма таза М'язи діафрагми тазаДеталіІдентифікаториЛатина Diaphragma pelvisАнатомічна термінологія[редагувати у Вікіданих] Діафрагма таза (лат. diaphragma pelvis) — м'язово-фасціальна перегородка, що разом з сеч�...

Ястремська Іванна ОлександрівнаЗагальна інформаціяГромадянство УкраїнаНародження 5 січня 2007(2007-01-05) (16 років)ОдесаЗріст 180 смСпортВид спорту тенісТренери Бесчарова Людмила Євгенівна Участь і здобутки У Вікіпедії є статті про інших людей із прізвищем Ястремська. Іва́

كالبة شعار الإحداثيات 51°54′12″N 11°46′33″E / 51.903333333333°N 11.775833333333°E / 51.903333333333; 11.775833333333 [1] تقسيم إداري البلد ألمانيا[2] التقسيم الأعلى زالتسلاندكرايس خصائص جغرافية المساحة 56.68 كيلومتر مربع (31 ديسمبر 2017)[3] ارتفاع 60 متر عدد ا

Pour la cérémonie des BAFTAs récompensant la télévision, voir la 3e cérémonie des British Academy Television Awards. 9e cérémonie des British Academy Film Awards BAFTA Awards Organisé par la British Academy of Film and Television Arts Détails Date 1956 Lieu Londres Royaume-Uni Diffusé sur BBC Site web http://www.bafta.org/ Résumé Meilleur film - toutes provenances Richard III Meilleur film britannique Richard III Film le plus nommé L'Emprisonné (5) Film le plus réco...

لمعانٍ أخرى، طالع عبد الجبار (توضيح). عبد الجبار تقسيم إداري البلد إيران إحداثيات 38°16′52″N 46°44′42″E / 38.281111°N 46.745°E / 38.281111; 46.745 تعديل مصدري - تعديل عبد الجبار هي قرية في مقاطعة هريس، إيران. عدد سكان هذه القرية هو 177 في سنة 2006.[1] مراجع ^ تعداد سكان ج
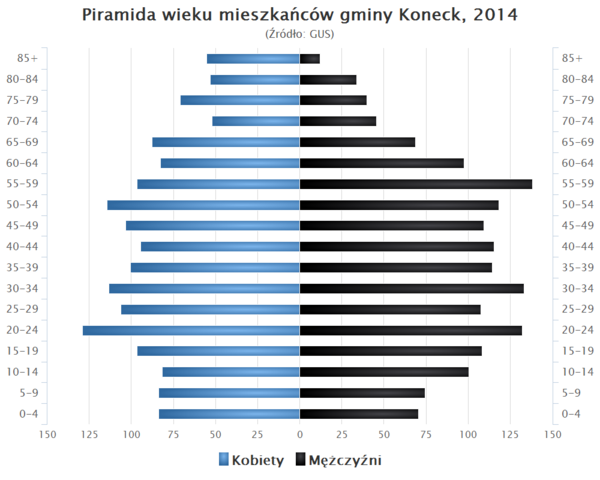
Koneck gmina wiejska Herb Flaga Państwo Polska Województwo kujawsko-pomorskie Powiat aleksandrowski TERC 0401062 Wójt Ryszard Władysław Borowski Powierzchnia 68,13 km² Populacja (31.12.2017)• liczba ludności 3177[1] • gęstość 46,6 os./km² Nr kierunkowy 54 Tablice rejestracyjne CAL Adres urzędu:ul. Włodzimierza Lubańskiego 1187-702 Koneck Szczegółowy podział administracyjny Liczba sołectw 19 Położenie na mapie województwa kujawsko-pomors...

Praia, Tanjung Verde (munisipalitas) Munisipalitas Lambang kebesaranLokasi di Tanjung VerdeNegara Tanjung VerdePulauSantiagoLuas • Total102,6 km2 (396 sq mi)Populasi (2010) • Total131.719 • Kepadatan130/km2 (330/sq mi)Kode ISO 3166-2CV-PRSitus webhttp://www.cmpraia.cv/ Praia adalah salah satu dari 22 munisipalitas di Tanjung Verde. Menurut sensus 2010, Praia memiliki luas 102,6 kilometer persegi dan populasi 131.719 jiwa. Kode ...

Commercial offices in Downtown Core, SingaporeUnited Overseas Bank PlazaChinese: 大华银行大厦Malay: Bangunan Bank UOBTamil: யூ.ஓ.பி பிளாசாUOB Plaza in 2006Alternative namesUnited Overseas Bank PlazaGeneral informationTypeCommercial officesLocationDowntown Core, SingaporeCoordinates1°17′08″N 103°50′59″E / 1.28555°N 103.84972°E / 1.28555; 103.84972Construction startedPlaza One: 1992CompletedPlaza One: 1995Plaza Two: 1973OwnerUn...

Claw beaker from an Anglo-Saxon site. Anglo-Saxon glass has been found across England during archaeological excavations of both settlement and cemetery sites. Glass in the Anglo-Saxon period was used in the manufacture of a range of objects including vessels, beads, windows and was even used in jewellery.[1] In the 5th century AD with the Roman departure from Britain, there were also considerable changes in the usage of glass.[2] Excavation of Romano-British sites have reveale...

المسرحThe Playhouseمعلومات عامةالتصنيف فيلم قصير الصنف الفني كوميدياتاريخ الصدور 1921مدة العرض 23 دقيقة العرض أبيض وأسود البلد الولايات المتحدة الأمريكيةالطاقمالمخرج باستر كيتون، إدوارد فرنسيس كلاينالسيناريو باستر كيتون، إدوارد فرنسيس كلاينالبطولة باستر كيتون فيرجينيا فوكس �...

Madame Élisabeth de France (1764–1794)ArtistAdélaïde Labille-Guiard Yearc. 1787Dimensions78.7 cm (31.0 in) × 65.4 cm (25.7 in)LocationMetropolitan Museum of ArtAccession No.2007.441 IdentifiersThe Met object ID: 439405[edit on Wikidata] Madame Élisabeth de France (1764–1794) is a painting by Adélaïde Labille-Guiard. It is in the collection of the Metropolitan Museum of Art.[1] Description and interpretation The work depicts Élisa...

Minimalist language created by Sonja Lang Toki Ponatoki ponaThe words toki pona written in sitelen ponaPronunciation[ˈtoki ˈpona]Created bySonja LangDate2001Setting and usageTesting principles of minimalism, the Sapir–Whorf hypothesis and pidginsUsers500 ~ 5000 (2021)[1]PurposeConstructed language, combining elements of the subgenres personal language and philosophical languageWriting systemLatin script; sitelen pona (logographic); sitelen sitelen (logographic wi...

American television judge from Louisiana For other people named Randy Jackson, see Randy Jackson (disambiguation). Randy JacksonJackson in March 2018Background informationBirth nameRandall Darius JacksonBorn (1956-06-23) June 23, 1956 (age 67)Baton Rouge, Louisiana, U.S.Occupation(s)Record executivetelevision presentermusicianrecord producerInstrument(s)BasskeyboardsYears active1983–presentLabelsDream Merchant 21ConcordColumbiaFormerly ofDivinylsJourneySpouse(s) Elizabeth Jackson ̴...
Questa voce sull'argomento cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Jim Springer Nazionalità Stati Uniti Altezza 206 cm Peso 107 kg Pallacanestro Ruolo Centro Termine carriera 1949 Carriera Giovanili 1944-1945 Ind. St. Sycamores1945-1947Canterbury College Squadre di club 1947-1948 Anderson Packers61948 Ind. Kautskys191948-1949 Indianapolis Jets2 Il...

Supercopa Endesa 2009Datos generalesSede Las Palmas de Gran Canaria EspañaRecinto Centro Insular de DeportesFecha 2 - 3 de octubre de 2009Edición 10.ªPalmarésPrimero FC Barcelona (3)Segundo Real MadridMVP Juan Carlos Navarro Cronología 2008 2009 2010 [editar datos en Wikidata] La Supercopa de España de Baloncesto 2009 fue la 6.ª edición del torneo desde que está organizada por la ACB y la 10.ª desde su fundación de un torneo de baloncesto disputado el 2 y 3 de octubr...

1975 live album by Max BoyceWe All Had Doctors' PapersLive album by Max BoyceReleased1975RecordedPontarddulais RFCGenreComedy, folkLanguageEnglish, WelshLabelEMIMB 101Max Boyce chronology Live at Treorchy(1974) We All Had Doctors' Papers(1975) The Incredible Plan(1976) We All Had Doctors' Papers is a live album by Welsh comedian and singer Max Boyce, first issued in 1975 and recorded at Pontarddulais Rugby Club. It was his fourth album release and followed his breakthrough recording L...

Embarcadero PlazaThe plaza in 2009Show map of San FranciscoShow map of San Francisco Bay AreaShow map of CaliforniaCoordinates37°47′42″N 122°23′41″W / 37.7949°N 122.3948°W / 37.7949; -122.3948Open1972Public transit accessBART and Muni, Embarcadero station Embarcadero Plaza, previously known as Justin Herman Plaza from its opening in 1972 until 2017, is a 1.23-acre (0.50 ha) plaza near the intersection of Market and Embarcadero in San Francisco's Financ...

La redacción de este artículo o sección debería adecuarse a las convenciones de estilo de Wikipedia. Puedes colaborar editándolo.Cuando se haya corregido, por favor borra este aviso, pero no antes. Este aviso fue puesto el 30 de diciembre de 2023. Este artículo o sección necesita una revisión de ortografía y gramática.Puedes colaborar editándolo. Cuando se haya corregido, puedes borrar este aviso. Si has iniciado sesión, puedes ayudarte del corrector ortográfico, activándolo en...

Earl of Lincoln John de la PoleEarl of LincolnBornc. 1460Died16 June 1487(1487-06-16) (aged 26–27)East Stoke, NottinghamshireSpouseMargaret FitzAlanHousede la PoleFatherJohn de la Pole, 2nd Duke of SuffolkMotherElizabeth of York John de la Pole, Earl of Lincoln (c. 1460 – 16 June 1487) was a leading figure in the Yorkist aristocracy during the Wars of the Roses. After the death of his uncle Richard III, de la Pole was reconciled with the new Tudor regime, but two years later he orga...










