Mathématiques financières
|
Read other articles:

ياسمين علي معلومات شخصية الميلاد 13 نوفمبر 1990 (33 سنة)[1] محافظة البحيرة[2] مواطنة مصر الحياة الفنية الآلات الموسيقية صوت بشري المهنة مغنية اللغة الأم العربية اللغات العربية مجال العمل غناء المواقع السينما.كوم صفحتها على السينما.كوم ت�...

Тійода — термін, який має кілька значень. Ця сторінка значень містить посилання на статті про кожне з них.Якщо ви потрапили сюди за внутрішнім посиланням, будь ласка, поверніться та виправте його так, щоб воно вказувало безпосередньо на потрібну статтю.@ пошук посилань сам

Slovak Jewish writer (1918–1988) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Alfréd Wetzler – news · newspapers · books · scholar · JSTOR (April 2017) (Learn how and when to remove this template message) Alfred WetzlerBornAlfred Israel Wetzler10 May 1918Nagyszombat, Austria-Hungary (present-day Trnava...

1964 film Blood TiesRussian: Родная кровьDirected byMikhail YershovWritten byFyodor Knorre (novel)Produced byAlexander ArshanskyStarring Yevgeny Matveev Vija Artmane CinematographyOleg KukhovarenkoEdited byAleksandra BorovskayaMusic byVeniamin BasnerProductioncompanyLenfilmRelease date1964Running time91 min.CountrySoviet UnionLanguageRussian Blood Ties (Russian: Родная кровь, romanized: Rodnaya krov) is a 1964 Soviet drama film directed by Mikhail Yershov.[1]...

BrontotheriumRentang fosil: Akhir Eosen kerangka Brontotherium hatcheri dari National Museum of Natural History, Washington, DC Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Perissodactyla Famili: Brontotheriidae Genus: Brontotherium Species B. gigas (type) B. leidyi B. hatcheri B. ingens B. platyceras Brontotherium (Hewan kilat') adalah genus hewan mamalia berkuku ganjil prasejarah dari famili Brontotheriidae, sekelompok hewan punah menyerupai badak yang berkera...

Motumarri–Vishnupuram sectionOverviewStatusOperationalOwnerIndian RailwaysLocaleTelanganaTerminiMotamarriVishnupuramStations10ServiceSystemSingle Electric Railway LineServicesDelhi–Chennai line Pagidipalli–Nallapadu sectionOperator(s)South Central Railway zoneHistoryOpened2019TechnicalLine length89 km (55 mi)Number of tracks1Track gauge5 ft 6 in (1,676 mm) broad gaugeElectrificationSingle-line overhead catenaryOperating speed151 km (94 mi) Route m...

Species of gastropod endemic to the Philippines Vittina waigiensis Vittina waigiensis from the Philippines Variability of the shell patterns of Vittina waigiensis Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Mollusca Class: Gastropoda Subclass: Neritimorpha Order: Cycloneritida Family: Neritidae Genus: Vittina Species: V. waigiensis Binomial name Vittina waigiensis(Lesson, 1831)[1] Synonyms[2] Neritina waigiensis Lesson, 1831 Vittina waigiensis, c...

Big Gastrin Names IUPAC name H-Pyr-Leu-Gly-Gly-Gln-Gly-Pro-Gly-Gly-Gly-Gly-Ala-Asp-Gly-Gly-Lys-Lys-Gln-Gly-Pro-Gly-Gly-Glu-Glu-Glu-Glu-Gly-Ala-Gly-Gly-Trp-Met-Asp-Phe-NH2 Systematic IUPAC name L-pyroglutamyl-L-leucyl-glycyl-glycyl-L-glutaminyl-glycyl-L-prolyl-glycyl-glycyl-glycyl-glycyl-L-alanyl-L-alpha-aspartyl-glycyl-glycyl-L-lysyl-L-lysyl-L-glutaminyl-glycyl-L-prolyl-glycyl-glycyl-L-alpha-glutamyl-L-alpha-glutamyl-L-alpha-glutamyl-L-alpha-glutamyl-glycyl-L-alanyl-glycyl-glycyl-L-tryptophyl...

Alexis Ford Información personalOtros nombres Nicole FTVNacimiento 24 de abril de 1988 (35 años)Glendale, Nueva York,Estados UnidosNacionalidad EstadounidenseEtnia CaucásicaLengua materna Inglés Características físicasAltura 1,63 m (5′ 4″)Peso 55 kg (121 lb)Medidas 33D-25-33Ojos AzulesCabello RubioFamiliaCónyuge Sebastien Lagree (2013)Información profesionalOcupación Actriz pornográficaAños activa 2008-2016Películas 204 (IAFD)[1]Seudónimo Alexis For...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: GCU London – news · newspapers · books · scholar · JSTOR (January 2018) (Learn how and when to remove this template message) A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia...

Phoenix 500NASCAR Cup SeriesTempatPhoenix RacewayLokasiAvondale, Arizona, United StatesSponsor korporasiRuoff Mortgage[1]Lomba pertama2005Jarak tempuh310.688 mi (500.004 km)Lap312Tahap 1: 75Tahap 2: 115Tahap akhir: 122Nama sebelumnyaSubway Fresh 500 (2005–2006) Subway Fresh Fit 500 (2007–2009, 2011–2013) Subway Fresh Fit 600 (2010)The Profit on CNBC 500 (2014) CampingWorld.com 500 (2015) Good Sam 500 (2016) Camping World 500 (2017) TicketGuardian 500 (2018–2019)FanSh...

Cette liste regroupe les guerres et conflits ayant vu la participation de l'Espagne. Voici une légende facilitant la lecture de l'issue des guerres ci-dessous : Victoire espagnole Défaite espagnole Autre résultat (par exemple un traité ou une paix sans un résultat clair, un statu quo ante bellum, un résultat inconnu ou indécis) Conflit en cours Monarchie catholique espagnole Début Fin Nom du conflit Belligérants Lieu Issue Alliés (y compris l'Espagne) Ennemis 15 avril1519 13 ao...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (January 2017) (Learn how and when to remove this template message) Standard Chinese vowels (with IPA and Pinyin) Front Central Back Close i ⟨i⟩ • y ⟨ü⟩ ɨ ⟨i⟩ u ⟨u⟩ ɤ ⟨e⟩ • o ⟨o⟩ e̞ ⟨ê⟩ ɚ ...

West Cork RallyCategoryRallyInaugural season1977Drivers' champion Craig BreenCo-Drivers' champion Paul NagleFord Fiesta R5Irish Tarmac Rally Championship Current season British Rally Championship Current season National Rally Championship (past)Southern 4 Rally Championship (past) West Cork RallyDates14 March 2020 (2020-03-14) - 15 March 2020 (2020-03-15) cancelledFrequencyAnnualLocation(s)County CorkCountryIrelandMost recent2019Organised byCork Motor ClubSponsor...

British TV series or programme Faking ItGenreRealityCreated byStephen LambertDirected byLance JefferyAdam KassenNarrated byMichael KitchenCountry of originUnited KingdomOriginal languageEnglishNo. of seasons9No. of episodes48 (list of episodes)ProductionRunning time60 minutes (inc. adverts)Production companyRDF TelevisionOriginal releaseNetworkChannel 4Release18 September 2000 (2000-09-18) –26 December 2006 (2006-12-26) Faking It is a television programme originating on ...

Opera by Hans Werner Henze The BassaridsOpera by Hans Werner HenzeThe composer in 1960Native titleDie BassaridenLibrettist W. H. Auden Chester Kallman Based onThe Bacchaeby EuripidesPremiere6 August 1966 (1966-08-06)Salzburg The Bassarids (in German: Die Bassariden) is an opera in one act and an intermezzo, with music by Hans Werner Henze to an English libretto by W. H. Auden and Chester Kallman, after Euripides's The Bacchae. The conflict in the opera is between human rational...

Television sitcom Dil Dosti DobaraAlso known as3DGenreSitcomCreated by Sanjay Jadhav Ashish Pathare Written byStory - Sanjay JadhavScreenplay and dialogues - Ashish Pathare Directed byVinod LavekarStarring Amey Wagh Pushkaraj Chirputkar Sakhi Gokhale Suvrat Joshi Swanandi Tikekar Pooja Thombare Country of originIndiaOriginal languageMarathiNo. of episodes152ProductionProducerSanjay JadhavCamera setupMulti-cameraRunning time22 minutesProduction companyDreaming 24/7 ProductionsOriginal releaseN...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Abhishek BachchanBachchan pada tahun 2015LahirAbhishek Bachchan5 Februari 1976 (umur 47)Bombay (sekarang: Mumbai), Maharashtra, IndiaPekerjaa...
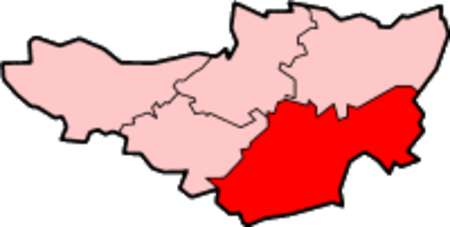
Human settlement in EnglandBuckland St MaryThe Old Rectory, Buckland St MaryBuckland St MaryLocation within SomersetPopulation521 (2011)[1]OS grid referenceST268132DistrictSouth SomersetShire countySomersetRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townChardPostcode districtTA20Dialling code01823PoliceAvon and SomersetFireDevon and SomersetAmbulanceSouth Western UK ParliamentTaunton Deane List of places UK England Somerset 5...

Pit to contain a fire This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fire pit – news · newspapers · books · scholar · JSTOR (July 2008) (Learn how and when to remove this template message) A fire pit A fire pit or a fire hole can vary from a pit dug in the ground to an elaborate gas burning structure of sto...

![{\displaystyle \mathbb {E} \left[A_{t}|{\mathcal {F}}_{s}\right]=A_{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fea89470c2463a4e91b0e525980383700427175)






