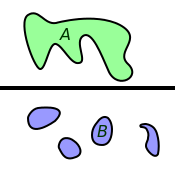
Connexité (mathématiques)
|
Read other articles:

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Dewi Sekardadu – berita · surat kabar �...

Prefecture and commune in Hautes-Pyrénées, Occitanie, France Prefecture and commune in Occitania, FranceTarbesPrefecture and communeThe town hall of Tarbes Coat of armsLocation of Tarbes TarbesShow map of FranceTarbesShow map of OccitanieCoordinates: 43°14′N 0°04′E / 43.23°N 0.07°E / 43.23; 0.07CountryFranceRegionOccitaniaDepartmentHautes-PyrénéesArrondissementTarbesCanton3 cantonsIntercommunalityCA Tarbes-Lourdes-PyrénéesGovernment • Mayor (2...

Chinese retired politician In this Chinese name, the family name is Zhang. Zhang Dejiang张德江9th Chairman of the Standing Committee of the National People's CongressIn office14 March 2013 – 17 March 2018DeputyLi JianguoLeaderXi JinpingPreceded byWu BangguoSucceeded byLi ZhanshuVice Premier of the People's Republic of ChinaIn office17 March 2008 – 16 March 2013Serving with Li KeqiangHui Liangyu, Wang QishanPremierWen JiabaoCommunist Party Secretary of Chon...

Ліберальні демократиангл. Liberal DemocratsКраїна Велика БританіяГолова партії Нік Клегг[1], Тім Фаррон, Sal Brintond, Тім Фаррон, Вінс Кейбл, Джо Свінсон, Mark Packd і Ед ДейвіДата заснування 3 березня 1988Штаб-квартира Лондон, ВестмінстерІдеологія Соціал-лібер�...

Senboku 仙北市Kota BenderaLambangLocation of Senboku in Akita PrefectureNegara JepangWilayahTōhokuPrefekturAkitaPemerintahan • WalikotaMitsuhiro KadowakiLuas • Total1,093,56 km2 (0,42.223 sq mi)Populasi (Oktober 1, 2019) • Total25.305 • Kepadatan23,1/km2 (600/sq mi)Zona waktuUTC+9 (Japan Standard Time)Simbol kota Nomor telepon0187-43-1111Alamat30 Miyanoshiro, Obonai, Tazawako, Semboku-shi, Akita-ken 01...

جزء من سلسلة مقالات سياسة فلسطينفلسطين الدستور القانون الأساسي الفلسطيني (الدستور) الميثاق الوطني حقوق الإنسان السلطة التنفيذية الرئيس محمود عباس مجلس الوزراء الفلسطيني رئيس الوزراء محمد اشتية السلطة التشريعية المجلس الوطني الفلسطيني المجلس التشريعي الفلسطيني السلطة �...

Datu Kalantiaw (Rajah Bendahara Kalantiaw) (kadang-kadang dieja Kalantiao) pernah dianggap sebagai bagian penting dari sejarah Filipina sebagai orang yang mencetuskan kodifikasi hukum pertama di Filipina, yang dikenal sebagai Kode Kalantiaw pada tahun 1433. Dia dianggap oleh orang Filipina, khususnya Visayas, sebagai kepala ketiga Panay (sebuah pulau di Visayas dengan empat provinsi: Aklan, Antique, Capiz dan Iloilo). Dia adalah sumber kebanggaan Filipina dan Visayan selama beberapa dasawarsa...

Untuk militan Slavofon di Makedonia Yunani pada masa Perang Dunia II, lihat Ohrana. OkhranaDepartemen untuk Perlindungan Keamanan dan Tatanan MasyarakatInformasi lembagaDibentuk1881[1]Dibubarkan1917Wilayah hukum Kekaisaran RusiaKantor pusatPetrograd Departemen untuk Perlindungan Keamanan dan Ketertiban Masyarakat (bahasa Rusia: Отделение по Охранению Общественной Безопасности и Порядка), yang biasanya disebut departemen pert...

Map all coordinates using: OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) This list is of the Cultural Properties of Japan designated in the category of historical materials (歴史資料, rekishi shiryō) for the Prefecture of Gunma.[1] National Cultural Properties As of 1 May 2015, one Important Cultural Property has been designated, being of national significance.[2][3][4] Property Date ...

Municipality of North Macedonia Rural municipality in Skopje, North MacedoniaPetrovec Municipality Општина ПетровецRural municipality FlagCountry North MacedoniaRegion SkopjeMunicipal seatPetrovecGovernment • MayorBorče Mitevski (VMRO-DPMNE)Area • Total201.93 km2 (77.97 sq mi)Population • Total8,255 • Density40.88/km2 (105.9/sq mi)Time zoneUTC+1 (CET)Area code031car platesSKWebsitehttp://www.opstina-petro...

2016 studio album by Deacon BlueBelieversStudio album by Deacon BlueReleased30 September 2016 (2016-09-30)Recorded2014–2016GenrePop, rockLength44:00LabelEarMusic, Sheer SoundProducerPaul SavageDeacon Blue chronology A New House(2014) Believers(2016) City of Love(2020) Believers is the eighth studio album released by Scottish band Deacon Blue, released on 30 September 2016 via both EarMusic and Sheer Sound recording labels. The album was a commercial success in the Uni...

Filipino Roman Catholic bishop The Most ReverendCirilo Reyes Almario, Jr.D.D.2nd Bishop of MalolosSeeMalolosIn office15 December 1977 - 20 January 1996PredecessorManuel P. del Rosario, D.D.SuccessorRolando T. Tirona, OCD, D.D.Other post(s)Vicar-Capitular of Lipa Titular Bishop of ZabaOrdersOrdination30 November 1956by Alejandro Olalia, D.D.Consecration18 October 1973by Brunio Torpigliani, D.D.Personal detailsBornCirilo Reyes Almario, Jr.(1931-01-11)January 11, 1931Caridad, Cavite, C...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها...

رومانيا دولة علمانية، وليس فيها دين للدولة. رومانيا أشدّ البلدان الأوروبية تديّنًا، ومعظم مواطنيها من المسيحيين الأرثوذكس.[1] تعترف الحكومة الرومانية رسميًّا بثمانية عشر دينًا وطائفة.[2] انتسب 81.04% من سكان رومانيا المستقرين إلى الكنيسة الأرثوذكسية الشرقية، في إحصا...

2010 Philippine television series First TimeTitle cardGenreRomantic dramaDeveloped byKit Villanueva-LangitDirected byAndoy RanayStarring Barbie Forteza Joshua Dionisio Jake Vargas Opening themeFirst Love by Rita IringanCountry of originPhilippinesOriginal languageTagalogNo. of episodes77ProductionExecutive producerJoseph BuncalanCamera setupMultiple-camera setupRunning time30-45 minutesProduction companyGMA Entertainment TVOriginal releaseNetworkGMA NetworkReleaseFebruary 8 (2010-02-08)&...

Airport in Maharashtra, India Gandhinagar AirportCombat Army Aviation Training SchoolIATA: ISK ICAO: VANRSummaryAirport typeMilitaryOwnerIndian ArmyOperatorIndian Army Aviation CorpsServesNashik, Maharashtra, India & Nashik Road-DevlaliLocationNashik RoadElevation AMSL483 m / 1,585 ftCoordinates19°57′49″N 073°48′27″E / 19.96361°N 73.80750°E / 19.96361; 73.80750MapsMaharashtra in IndiaVANRLocation of the airport in MaharashtraRunways Direc...

Spanish footballer In this Spanish name, the first or paternal surname is Sanchís and the second or maternal family name is Martínez. Manuel Sanchís Sanchís in 1966Personal informationFull name Manuel Sanchís MartínezDate of birth (1938-03-26)26 March 1938Place of birth Alberic, SpainDate of death 28 October 2017(2017-10-28) (aged 79)Place of death Madrid, SpainHeight 1.71 m (5 ft 7 in)Position(s) DefenderSenior career*Years Team Apps (Gls)1955–1961 Condal ...

53°47′40″N 1°32′30″W / 53.794582°N 1.541720°W / 53.794582; -1.541720 View of the New Penny from Call Lane in 2010 Leeds Civic Trust Blue Plaque The New Penny is a gay pub in The Calls area of Leeds, West Yorkshire. It is reported to be the oldest continually running gay pub in the UK. History The pub started as the Hope and Anchor in 1953. Although difficulty with the law meant it was a secretive place, it was the first gay venue to open outside London.[...

Proposed road tunnel Traffic on the A303 road passing by Stonehenge The Stonehenge road tunnel is a planned tunnel in Wiltshire, England, drawn up by National Highways to upgrade the A303 road. It would move the A303 into a tunnel under the Stonehenge World Heritage Site, completing the removal of traffic begun with the 2012 closure of the A344 road.[1] The wider project was designed to improve the landscape around the monument and to improve safety on the A303,[2] and was par...

British Army officer, courtier and Whig politician Not to be confused with Conyers Darcy, 7th Baron Darcy de Knayth (1570–1653), Conyers Darcy, 1st Earl of Holderness (1598/1599 – 1689), or Conyers Darcy, 2nd Earl of Holderness (1622–1692). Sir Conyers Darcy or Darcey, KCB PC (c. 1685 – 1 December 1758), of Aske, near Richmond, Yorkshire, was a British Army officer, courtier and Whig politician who sat in the House of Commons between 1707 and 1758. Early life Aske Hal...