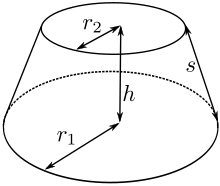
Cône de révolution
| |||||||||||||||||||||
Read other articles:

لمعانٍ أخرى، طالع ريال (توضيح). ريال سعوديمعلومات عامةالبلد السعوديةتاريخ الإصدار 1935[1] رمز العملة ر. سرمز الأيزو 4217 SARالمصرف المركزي البنك المركزي السعوديموقع المصرف المركزي www.sama.gov.saسعر الصرف دولار أمريكي = 3.75 ريال سعوديالعملات المعدنية 1 هللة، 5 هللات، 10 هلل�...

屏東縣立來義高級中學地址屏東縣來義鄉古樓村中正路147號[1]其它名称Pingtung County Lai yi Senior High School类型普通型高級中等學校、完全中學创办日期1968年8月学区 中華民國屏東縣來義鄉校長陳冠明校訓誠·正·勤·樸電話號碼(08)7850086[1]学校网址http://web.lyhs.ptc.edu.tw 屏東縣立來義高級中學,簡稱來義高中、來中,於1967年成立籌備處,並於1968年8月正式成立。2002年...

العمل المأجور ورأس المالLohnarbeit und Kapital (بالألمانية) معلومات عامةالمؤلف كارل ماركس اللغة الألمانية النوع الأدبي مقالة تاريخ الإصدار 1849 تعديل - تعديل مصدري - تعديل ويكي بيانات 'كارل ماركس' و'فريدريك اينغلس' العمل المأجور ورأس المال (بالألمانية: Lohnarbeit und Kapital) مقالة عن الاقتصاد �...

House of Representatives of the Philippines legislative district Agusan del Norte's 1st congressional districtConstituencyfor the House of Representatives of the PhilippinesLocation of Agusan del Norte within the PhilippinesProvinceAgusan del NorteRegionCaragaPopulation403,150 (2020)[1]Electorate238,541 (2019)[2]Major settlements 2 LGUs Cities Butuan Municipalities Las Nieves Area1,399.31 km2 (540.28 sq mi)Current constituencyCreated1987RepresentativeJose Aquino...

The Fabulous UdinPoster filmSutradara Herdanius Larobu Produser Chand Parwez Servia Ditulis oleh Rons Imawan PemeranAjil DittoBella GracevaAldy RialdyDifa RyansyahZulfa MaharaniRaza AdhanzioMusdalifah BasriLidya KandouFandy ChristianFendy ChowStella CorneliaUssy SulistiawatyIqbal PakulaMasayu AnastasiaYama CarlosBudi DaltonRobby SugaraBene DionJoshua PandelakiPenata musikThe OvertunesPerusahaanproduksiStarvisionDistributorStarvision PlusTanggal rilis 12 Mei 2016Negara IndonesiaBahasa In...

العلاقات الرواندية السورينامية رواندا سورينام رواندا سورينام تعديل مصدري - تعديل العلاقات الرواندية السورينامية هي العلاقات الثنائية التي تجمع بين رواندا وسورينام.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ا�...

Untuk Keuskupan, lihat Daftar keuskupan di Indonesia. Berikut adalah daftar paroki di Indonesia yang dikelompokkan berdasarkan wilayah Keuskupan. Daftar ini diolah dari beberapa sumber. A.Medan Padang Sibolga A.Palembang Pangkal Pinang Tanjungkarang Bogor A.Jakarta Bandung A.Semarang Malang Purwokerto Surabaya A.Pontianak Palangkaraya A.Samarinda Ketapang Sanggau Sintang Tanjung Selor Banjarmasin Manado A.Makassar Denpasar A.Ende Larantuka Maumere Ruteng A.Kupang Atambua Weetebula Amboina A.M...

Culinary traditions of Sri Lanka This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2020) (Learn how and when to remove this template message) Traditional Sri Lankan rice and curry Sri Lankan cuisine is known for its particular combinations of herbs, spices, fish, vegetables, rices, and fruits. The cuisine is highly centered around many varieties of rice, ...

محمد زهير البابا معلومات شخصية الميلاد سنة 1921 القيمرية الوفاة 1 سبتمبر 2011 (89–90 سنة) دمشق مواطنة دولة دمشق (1921–1925) الدولة السورية (1925–1932) الجمهورية السورية الأولى (1932–1958) الجمهورية العربية المتحدة (1958–1961) سوريا (1961–1 سبتمبر 2011) عضو في الموسوعة العربية، ...

You can help expand this article with text translated from the corresponding article in French. (November 2016) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikip...
Австралія на Олімпійських іграх Код МОК:AUS НОК:Національний олімпійськийкомітет Австралії Участь у літніх Олімпійських іграх 1896 • 1900 • 1904 • 1908—1912 • 1920 • 1924 • 1928 • 1932 • 1936 • 1948 • 1952 • 1956 • 1960 • 1964 • 1968 • 1972 • 1976 • 1980 • 1984 • 1988 • 1992 • 1996 • 2000 • 2004 • 2008 • 2012 • 2016 • 2020 Уч...

Spanish general and colonial governor (1762–1821) In this Spanish name, the first or paternal surname is O'Donojú and the second or maternal family name is O'Ryan. The Most ExcellentJuan O'DonojúJefe Político Superior, 62nd Viceroy of New SpainIn office3 August 1821 – 27 September 1821MonarchFerdinand VII of SpainPreceded byJuan Ruiz de Apodaca, 1st Count of VendettaSucceeded byAgustín de Iturbide (President of the Regency of the Mexican Empire)Regent of the Mexican E...

1938 film by Christy Cabanne Night SpotNewspaper advertisementDirected byChristy CabanneScreenplay byLionel HouserBased onShe Sang for Her Supperby Anne JordanProduced byRobert SiskStarringHarry ParkeAllan LaneGordon JonesJoan WoodburyLee PatrickCinematographyNicholas MusuracaEdited byHarry MarkerMusic byRoy WebbProductioncompanyRKO PicturesDistributed byRKO PicturesRelease date February 25, 1938 (1938-02-25) Running time60 minutesCountryUnited StatesLanguageEnglish Night Spot ...

48°22′04″ с. ш. 10°53′35″ в. д.HGЯO Церковный регион Аугсбурга и Швабии (нем. Kirchenkreis Augsburg und Schwaben) ШвабияЦерковный регион АугсбургЦерковный регион Аугсбург с деканатами: 4 Аугсбург, 15 Донаувёрт, 28 Кемптен, 37 Мемминген, 44 Ной-Ульм, 45 Нёрдлинген, 47 ЭттингенБазовая инфор�...

Paramilitary group in Myanmar This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs to be updated. Please help update this article to reflect recent events or newly available information. (April 2021) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and remo...

In this Chinese name, the family name is Chan. Chan ShenChan ShenBornChan Yi-Cheng(1940-03-11)11 March 1940Taichung, TaiwanDied26 April 1984(1984-04-26) (aged 44)Hong KongOccupationactorYears active1971—1984Chinese nameTraditional Chinese詹森Transcriptions Chan Shen (11 March 1940 - 26 April 1984) was a Taiwanese-born Hong Kong film actor. He is best known for his roles as gangsters or villains in Hong Kong action cinema in the 1970s. Already an established film actor in Ta...

2023 studio album by the ViewExorcism of YouthStudio album by the ViewReleased18 August 2023 (2023-08-18)StudioEl Mirador, Granada, SpainGenreIndie rock[1]Length47:21LabelCooking VinylProducerYouthThe View chronology Ropewalk(2015) Exorcism of Youth(2023) Exorcism of Youth is the sixth studio album by Scottish indie rock band the View, released on 18 August 2023 through Cooking Vinyl. It is the band's first album in eight years, following Ropewalk (2015) and the...

For the category of flamenco, see Tientos (Flamenco). Tiento (Spanish pronunciation: [ˈtjento], Portuguese: Tento [ˈtẽtu]) is a musical genre originating in Spain in the mid-15th century. It is formally analogous to the fantasia (fantasy), found in England, Germany, and the Low Countries, and also the ricercare, first found in Italy. By the end of the 16th century the tiento was exclusively a keyboard form, especially of organ music. It continued to be the predominant form...

South Korean television show Handsome TigersHangul진짜 농구 핸섬타이거즈 GenreReality showBasketballDirected byAhn Jae-cheolJo Young-jaeYoon Jong-hoKim Eun-jiStarringSeo Jang-hoonJoyLee Sang-yoonKim Seung-hyun [ko]Seo Ji-seokJulien KangShorry [ko]Kang Kyung-joonMoon Su-innLee Tae-sunCha Eun-wooYoo Seon-hoKang In-sooJeon Ji-hoonCountry of originSouth KoreaOriginal languageKoreanNo. of seasons1No. of episodes12ProductionProduction locationSouth KoreaRunning t...

For the 19th-century fortress in the Polish capital, see Warsaw Citadel. A preserved Tobruk-type pillbox in Warsaw. It is one of 12 pillboxes built as part of the 1945 Festung. In the German language, Festung Warschau (Fortress Warsaw) is the term used to refer to a fortified and well-defended Warsaw. In the 20th century, the term was in use on three occasions during World War I and World War II. It was used when the Germans threw back the Russian advance in 1914, where Warsaw came within dis...