Algèbre de Kac-Moody
|
Read other articles:

ليفركوزن علم شعار الاسم الرسمي (بالألمانية: Leverkusen) الإحداثيات 51°02′00″N 6°59′00″E / 51.033333333333°N 6.9833333333333°E / 51.033333333333; 6.9833333333333 [1] تاريخ التأسيس 1930 تقسيم إداري البلد ألمانيا[2][3] التقسيم الأعلى مقاطعة كولونيا خصائص جغرافي

NBA Fastbreak kan verwijzen naar: NBA Fastbreak (televisieprogramma), studio-programma dat uitgezonden wordt op ESPN NBA Fastbreak (flipperkast), flipperkastspel uit 1997 Bekijk alle artikelen waarvan de titel begint met NBA Fastbreak of met NBA Fastbreak in de titel. Dit is een doorverwijspagina, bedoeld om de verschillen in betekenis of gebruik van NBA Fastbreak inzichtelijk te maken. Op deze pagina staat een uitleg van de verschillende betekenissen van NBA Fastbrea...

У Вікіпедії є статті про інших людей із прізвищем Родрігес. Андрес РодрігесAndrés Rodríguez ісп. Andrés Rodríguez Pedotti Президент Парагваю 3 лютого 1989 — 15 серпня 1993Попередник Альфредо СтресснерНаступник Хуан Карлос ВасмосіНародився 19 червня 1923(1923-06-19)Borjad, Ґуайра, ПарагвайПомер 21 �...

American baseball player Baseball player Stoney McGlynnPitcherBorn: (1872-05-26)May 26, 1872Lancaster, PennsylvaniaDied: August 26, 1941(1941-08-26) (aged 69)Manitowoc, WisconsinBatted: RightThrew: RightMLB debutSeptember 20, 1906, for the St. Louis CardinalsLast MLB appearanceSeptember 2, 1908, for the St. Louis CardinalsMLB statisticsWin–loss record17–33Earned run average2.95Strikeouts157 Teams St. Louis Cardinals (1906–1908) Ulysses Simpson Grant St...

Grande Prêmio da Françade Fórmula 1 de 1992 Segundo GP da França realizado em Magny-Cours Detalhes da corrida Categoria Fórmula 1 Nome oficial Rhône-Poulenc Grand Prix de France Local Circuito de Magny-Cours, Magny-Cours, Borgonha-Franco-Condado, Departamento de Nièvre, França Total 69 voltas / 293.250 km Condições do tempo Seco, depois chuvoso Pole Piloto Nigel Mansell Williams-Renault Tempo 1:13.864 Volta mais rápida Piloto Nigel Mansell Williams-Renault Tempo 1:17.070 (na volta ...

Lumsden Hare 1922 Francis Lumsden Hare (* 17. Oktober 1874 oder 27. April 1875 in Tipperary, Munster, Irland[1]; † 28. August 1964 in Beverly Hills, Kalifornien, Vereinigte Staaten) war ein irischer Film- und Theaterschauspieler, der über Jahrzehnte in den USA arbeitete. Inhaltsverzeichnis 1 Leben 2 Filmografie (Auswahl) 3 Weblinks 4 Einzelnachweise Leben Lumsden Hare wanderte in jungen Jahren von Irland in die USA aus. Am Broadway in New York war er zwischen 1900 und 1942 in über...

Kerr after crashing out of an F3 race at Castle Combe in 2002. Robert Robbie Kerr (lahir 26 September 1979) adalah seorang pembalap mobil professional asal Inggris. Ia terkenal semenjak menjadi andalan utama tim Great Britain dalam ajang balapan A1GP. Selain di A1GP, ia bersama pembalap Kanada, Sean McIntosh juga bergabung di ajang World Series by Renault pada musim 2006 lalu. Pranala luar Official website of Robbie Kerr Diarsipkan 2008-05-11 di Wayback Machine. Robbie Kerr biography Artikel ...

متلازمة التأقلم في الفضاء معلومات عامة الاختصاص طب الفضاء من أنواع داء الحركة، ومرض تعديل مصدري - تعديل رواد الفضاء في ناسا يحاولون أقلمة أنفسهم مع متلازمة التأقلم في الفضاء في طائرة كي سي-135. متلازمة التأقلم في الفضاء أو دوار الفضاء أو متلازمة التكيف الفضائي (ب

Term for the Early Middle Ages This article is about the concept of a Dark Age in Western Europe after the Fall of the Western Roman Empire. For Greece after the Late Bronze Age collapse, see Greek Dark Ages. For other uses, see Dark Ages (disambiguation). Petrarch (1304–1374), who conceived the idea of a European Dark Age. From Cycle of Famous Men and Women, Andrea di Bartolo di Bargilla, c. 1450 The Dark Ages is a term for the Early Middle Ages or occasionally the entire Middle Ages, in W...

Kepolisian Resor MalangLambang Polres Malang IndonesiaSingkatanPolres MalangMottoHarkamtibmas, Penegak Hukum, Pelindung, Pengayom, dan Pelayan MasyarakatStruktur yurisdiksiWilayah hukumJawa TimurPeta wilayah Yurisdiksi Polres MalangYurisdiksi hukumKabupaten MalangLembaga pemerintahKepolisian Negara Republik IndonesiaKategoriPolisi sipilStruktur operasionalPengawasKepolisian Daerah Jawa TimurMarkas besarJl. Jend. A. Yani No. 1, Kepanjen, Kabupaten MalangPejabat eksekutifAKBP Putu Kholis A...

Royal borough in London, England Place in United KingdomRoyal Borough ofKingston upon ThamesLondon borough, Royal borough Coat of armsCouncil logoKingston upon Thames shown within Greater LondonSovereign stateUnited KingdomConstituent countryEnglandRegionLondonCeremonial countyGreater LondonCreated1 April 1965Admin HQKingston upon ThamesGovernment • TypeLondon borough council • BodyKingston upon Thames London Borough Council • LeadershipLiberal Democrat (Li...

1972 filmLucifera: Demon LoverDirected byPaolo LombardoScreenplay byPaolo Lombardo[1]Produced byDick Randall[1]Starring Edmund Purdom Rosalba Neri Spartaco Conversi CinematographyAntonino ModicaEdited byFrancesco Bertuccioli[1]Music byElvio Monti[1]ProductioncompanyNova International Film[1]Distributed byRegionalRelease date 26 January 1972 (1972-01-26) (Italy) Running time79 minutes[1]CountryItaly[1] Lucifera: Demon L...

Filipino politician from the province of Zamboanga del Norte In this Philippine name, the middle name or maternal family name is Yu and the surname or paternal family name is Uy. The HonorableRoberto UyGovernor of Zamboanga del NorteIn officeJune 30, 2013 – June 30, 2022Vice GovernorSenen O. AngelesPreceded byRolando E. YebesSucceeded byRosalina G. Jalosjos18th Mayor of DipologIn officeJune 30, 1998 – June 30, 2007Vice MayorEdelburgo L. ChengSenen O. AngelesPrec...

PromiseBackground informationBirth namePromise Jason Jamal ShepherdOriginToronto, OntarioGenresHip hop soulOccupation(s)Rapper, singer, songwriterYears active2002–presentLabelsDuck Down MusicWebsiteipromisemusic.comMusical artist Promise Jason Jamal Shepherd, professionally known as Promise, is a Canadian rapper from Toronto.[1] He is also 1/2 of Hip-Hop supergroup Perfeck Strangers, based in Scarborough, Ontario. Promise has collaborated with Jhené Aiko, Montell Jordan, LeCrae, No...

Australian politician The Honourable SirJohn SeeKCMG JP14th Premier of New South WalesIn office28 March 1901 – 14 June 1904Preceded byWilliam LyneSucceeded byThomas WaddellConstituencyGrafton Personal detailsBorn(1844-10-14)14 October 1844Yelling, Huntingdonshire, EnglandDied31 January 1907(1907-01-31) (aged 62)Randwick, New South Wales, AustraliaSpouseCharlotte Mary Matthews (1876–1904)Children Charlotte I. A. (m. Hordern) John Charles Matthews Ruby Edith S. Percy Georg...

Hokusei Gakuen University北星学園大学TypePrivateEstablished1962EndowmentN/AChancellorShinji KanaiAcademic staff117 full-time19 part-timeStudents4337Undergraduates4284Postgraduates53LocationSapporo, Hokkaidō, JapanCampusUrbanWebsitewww.hokusei.ac.jp Hokusei Gakuen University (北星学園大学, Hokusei Gakuen daigaku) is a four-year private university in Atsubetsu-ku, Sapporo, Hokkaidō, Japan. The university is run by Hokusei Gakuen School System, whose education philosophy is based o...

American actress (1937–2008) Pleshette redirects here. Not to be confused with Pleshet. Suzanne PleshettePublicity photo of Pleshette from the television program The Contenders c. 1963Born(1937-01-31)January 31, 1937New York City, U.S.DiedJanuary 19, 2008(2008-01-19) (aged 70)Los Angeles, California, U.S.Resting placeHillside Memorial Park Cemetery, Culver CityAlma materFinch CollegeNeighborhood Playhouse School of the TheatreOccupationActressYears active1958–2004Know...

Mexican politician Elizabeth Yáñez RoblesBorn (1945-09-29) 29 September 1945 (age 78)Torreón, Coahuila, MexicoAlma materCelaya Institute of TechnologyCharles III University of MadridOccupationDeputyPolitical party PAN Elizabeth Oswelia Yáñez Robles (born 29 September 1945) is a Mexican politician affiliated with the PAN. As of 2013 she served as Deputy of both the LIX and LXII Legislatures of the Mexican Congress representing Guanajuato.[1] References ^ Perfil del ...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (March 2018) In 1372, Khams paid allegiance to Ming dynasty, Khamas Guard was set a year later. It was reformed to a Military Commission (Chinese:朵甘行都指挥使司) in 1374. It was abandoned when the Tumed Mongols expanded in the period of Wanli.[1][2][3] References ^ 高文德 (1995). 中国少数民族�...
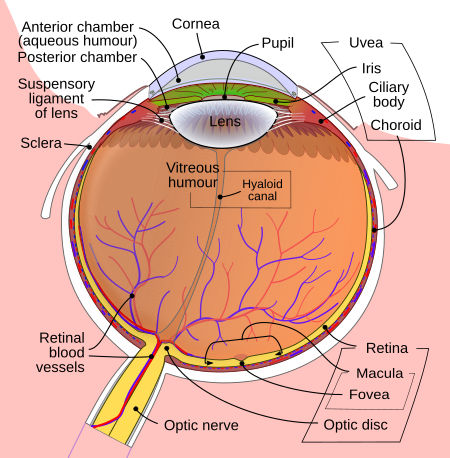
Space in the eye occupied by vitreous humor Vitreous chamberSchematic diagram of the human eyeDetailsIdentifiersLatincamera postrema; camera vitrea[1]TA98A15.2.06.006TA26807FMA58848Anatomical terminology[edit on Wikidata] The vitreous chamber is the largest of the three chambers in the eye and is located behind the lens and in front of the optic nerve. The vitreous chamber is located in the posterior cavity of the eye. This chamber is occupied with a thick, clear gel-like substanc...











![{\displaystyle [e_{i},f_{i}]=\alpha _{i}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5f11ae19c6ad273474304a9d187edbb6151e04a)
![{\displaystyle \forall {i}\neq j,[e_{i},f_{j}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c5d018b1178b5d4d009e2695c0f08b5a3ae381f)
![{\displaystyle \forall {x}\in {\mathfrak {E}},[e_{i},x]=\alpha _{i}^{*}(x)e_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b39da6929f94306196dfe43acbd6d5020377109b)
![{\displaystyle \forall {x}\in {\mathfrak {E}},[f_{i},x]=-\alpha _{i}^{*}(x)f_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c83bf4df752ec67173cc07dadfaa48e57d63d8c3)
![{\displaystyle \forall {x,x'}\in {\mathfrak {E}},[x,x']=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0533549c62b07cc3ecee49e6abd2e0792f7c844a)


![{\displaystyle {\textrm {ad}}:{\mathfrak {g}}\to {\textrm {gl}}({\mathfrak {g}}),{\textrm {ad}}(x)(y)=[x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acab3da310a24f74bb273e67bb5dc4d5ad1e0e53)

![{\displaystyle \forall {x}\in {\mathfrak {h}},[g,x]=\omega (x)g}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7985c350cda5e409a5fb36401ce7da3e6c67f094)



![{\displaystyle [e_{i},f_{j}]=0\ \forall {i}\neq {j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2abe0a35e69bf91ac928a8a0900600d478693d3c)
