Équation d'orbite
|
Read other articles:

Turid Knaak Turid Knaak en 2019Datos personalesNacimiento Essen, Alemania24 de enero de 1991 (32 años)Nacionalidad(es) alemanaAltura 1,68 m (5′ 6″)Peso 53 kg (117 lb)Carrera deportivaDeporte FútbolClub profesionalDebut deportivo 19 de agosto de 2007(FCR 2001 Duisburgo)Club VfL WolfsburgoLiga BundesligaPosición extremoDorsal(es) 33Selección nacionalSelección Selección de AlemaniaDorsal(es) 22Part. (goles) 16 (2)Trayectoria FCR 2001 Duisburgo (2007-11) Bayer 0...
Bahman Salemiinjehboroun Bahman Salemiinjehboroun Voleibol de praia Nome completo Bahman Salemiinjehboroun Representante Irão Nascimento 15 de janeiro de 1989 (34 anos)Gonbad-e Qābus, Golestan Nacionalidade iraniano Compleição Peso: 85 kg • Altura: 1,90 m Nível Profissional Medalhas Competidor do Irão Campeonato Asiático de Vôlei de Praia Ouro Songkhla 2017 Dupla Prata Satun 2018 Dupla Bahman Salemiinjehboroun (Gonbad-e Qābus, 15 de janeiro de 1989) é um voleib...

Judengasse WappenStraße in Weißenburg in Bayern Basisdaten Ort Weißenburg in Bayern Ortsteil Altstadt Angelegt Mittelalter Bauwerke Doppelhaus Judengasse 27 und 29 Technische Daten Straßenlänge ca. 230 Meter Die Judengasse ist eine Innerortsstraße in Weißenburg in Bayern, einer Großen Kreisstadt im mittelfränkischen Landkreis Weißenburg-Gunzenhausen. Sie bildet eine ost-west-gerichtete Gasse in der unter Ensembleschutz stehenden Altstadt Weißenburgs. Inhaltsverzeichnis 1 Geschichte...

Мірзо Турсун-задеМирзо Турсунзода Мірзо Турсун-задеНародився 19 квітня (2 травня) 1911(1911-05-02)с. Каратаг, Бухарський еміратПомер 24 вересня 1977(1977-09-24) (66 років)Душанбе, Таджицька РСРГромадянство СРСРДіяльність поетМова творів таджицька і російськаНапрямок соціалістичний ре

1701 play Sir Harry WildairWritten byGeorge FarquharDate premieredApril 1701Place premieredDrury Lane TheatreOriginal languageEnglishGenreRestoration Comedy Sir Harry Wildair is a 1701 comic play by the Irish writer George Farquhar. It is a sequel to the 1699 hit The Constant Couple, portraying the further adventures of the most popular character from the earlier play.[1] The original Drury Lane cast included Robert Wilks as Sir Harry Wildair, John Mills as Colonel Standard, Benjamin ...

Igreja Malankara Igreja MalankaraCruz Nasrani Orientação Cristianismo sírio Fundador São Tomé (Conforme a Tradição) Origem 52 dC (tradição);1665, separada da Igreja do Oriente Sede Kottayam, Kerala Líder espiritual Metropolita de Malankara Países em que atua Índia (Kerala) O Commons possui uma categoria com imagens e outros ficheiros sobre Igreja Malankara A Igreja Malankara ou Igreja Síria Malankara, também conhecida como Puthenkur e mais popularmente como Sírios Jacobit...

Artikel ini tidak memiliki referensi atau pranala luar ke sumber-sumber tepercaya yang dapat menyatakan kelayakan dari subyek yang dibahas.(ajukan diskusi keberatan penghapusan)Artikel ini akan dihapus pada 1 November 2023 jika tidak diperbaiki.Untuk pemulai artikel ini, jika Anda mempertentangkan nominasi penghapusan ini, jangan menghapus peringatan ini. Silakan hubungi sang pengusul, hubungi seorang pengurus, atau pasang tag {{tunggu dulu}} Artikel ini memiliki bebe...

Thành ủy Hà Nội Đảng kỳ Đảng Cộng sản Việt Nam Khóa thứ XVI (2020 - 2025) Cơ cấu Thành ủy Bí thư Đinh Tiến Dũng Phó Bí thư Thường trực (1) Nguyễn Thị Tuyến Phó Bí thư (3) Trần Sỹ ThanhNguyễn Ngọc Tuấn Nguyễn Văn Phong Ủy viên Thường vụ Thành ủy (16) Ban Thường vụ Thành ủy khóa XVII Thành ủy viên (71) Ban Chấp hành Đảng bộ Thành phố khóa XVII Cơ cấu tổ chức Cơ quan chủ quản Ban ch�...

1984 single by Musical Youth She's TroubleSingle by Musical Youthfrom the album Different Style! B-sideYard Stylee (US)Tell Jack (UK)ReleasedNovember 1983 (US)Recorded1981Genre Reggae pop rock[1] Length3:06LabelMCASongwriter(s) Billy Livsey Terry Britten Sue Shifrin Producer(s)Peter CollinsMusical Youth singles chronology Sixteen (1983) She's Trouble (1983) Whatcha Talking 'Bout (1984) Music videoShe's Trouble (Musical Youth) on YouTube She's Trouble, also known as Trouble, is a song ...

التطورية (قابلية التطور-evolvability) هي مفهوم في علم الأحياء التطوري الذي يحاول قياس قدرة الكائنات الحية على التطور.[1][2][3] على الرغم من عدة تعاريف ممكنة، التطورية على نطاق واسع هي قدرة الكائنات الحية على توليد التنوع الجيني من خلال تطور الانتقاء الطبيعي، ليكون أفضل ...
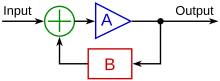
Model suatu umpan balik negatif ke bagian masukan, jika nilai B < 0 Umpan balik (bahasa Inggris: feedback) adalah suatu proses bahwa sebagian dari keluaran diumpanbalikkan ke bagian masukan. Hal ini sering dipakai untuk pengendalian suatu sistem yang bersifat dinamis sehingga sistem tersebut dapat diatur untuk mencapai keadaan stabil yang diinginkan. Beberapa contohnya dapat dijumpai pada sistem kompleks yang dipakai di bidang rekayasa, instrumentasi, elektronika, termodinamika, biolog...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Eko DaniyantoDirtipidnarkoba Bareskrim PolriMasa jabatan14 November 2016 – 2 Februari 2020PendahuluDharma PongrekunPenggantiKrisno Halomoan Siregar Informasi pribadiLahir15 Maret 1963 (umur 60)JakartaAlma materAkademi Kepolisian (1986)...
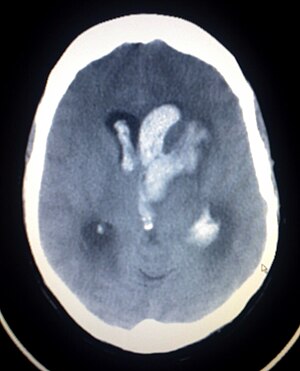
Hemorrhage, or bleeding, within the skull Medical conditionIntracranial hemorrhageAxial CT scan of a spontaneous intracranial hemorrhageSpecialtyEmergency medicine SymptomsSame symptoms as ischemic stroke, but unconsciousness, headache, nausea, stiff neck, and seizures are more often in brain hemorrhages than ischemic strokesComplicationsComa, persistent vegetative state, cardiac arrest (when bleeding is in the brain stem or is severe), deathTypesIntracerebral hemorrhage, subarachnoid he...

Nachzeichnung der Papiermühle („Cellulose“) etwa 1920 Der ehemalige Kollergang der Papiermühle in Alzenau. Ausgestellt im Mühlweg. Die Papiermühle, auch Stahlmühle oder Habermühle genannt, war eine Wassermühle in Alzenau im Landkreis Aschaffenburg in Bayern. Aus ihr ging die spätere Cellulosefabrik (heute Wellpappe) hervor. Inhaltsverzeichnis 1 Geographie 2 Geschichte 3 Siehe auch 4 Weblinks 5 Einzelnachweise Geographie Die Papiermühle stand im unteren Kahlgrund in Alzenau am Ran...

Defunct airline Nigeria Airways IATA ICAO Callsign WT NGA NIGERIA Founded23 August 1958 (1958-08-23) (after the dissolution of WAAC)Commenced operations1 October 1958 (1958-10-01)Ceased operations2003 (2003)HubsMurtala Muhammed International AirportSecondary hubsMallam Aminu Kano International AirportFocus citiesPort Harcourt International AirportDestinations9 (at the time of closure)Parent companyGovernment of Nigeria (100%)HeadquartersAbuja, FCT, NigeriaKe...

2002 video gameBikini Karate BabesDeveloper(s)Creative Edge StudiosPlatform(s)Microsoft Windows, macOSRelease2002Genre(s)FightingMode(s)Up to 2 players with 10 available modes Bikini Karate Babes is a 2002 2D fighting video game that uses digitized graphics, developed by Creative Edge Studios. It features an all-female cast of 19 fighters, all clad in bikinis and played by real actresses. The game was developed as a response to the treatment of women in contemporary fighting games, who would ...

2020 single by Nelly and Florida Georgia Line For the 50 Cent song, see Just a Lil Bit. For other uses, see Lil Bit (disambiguation). Lil BitSingle by Nelly and Florida Georgia Linefrom the album Heartland ReleasedOctober 23, 2020 (2020-10-23)Genre Hip hop country rap Length3:15Label Records Columbia BMLG Songwriter(s) Tyler Hubbard Blake Redferrin Cornell Haynes Jr. Jordan Schmidt Producer(s)Jordan SchmidtNelly singles chronology Good Times Roll (2020) Lil Bit (2020) High Hors...

First edition(publ. George G. Harrap & Co.) Clash is a 1929 novel by the English socialist politician Ellen Wilkinson. It focuses on the clash between career and personal relationships, against the backdrop of the 1926 general strike.[1][2] It was Wilkinson's first novel. It was republished by Trent Editions with a new introduction by Ian Haywood and Maroula Joannou in 1998. and is still in print. Ellen Wilkinson, the first woman Labour MP, is best remembered for leading a...

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) 1998 studio album by DiabolicSupreme EvilStudio album by DiabolicReleasedCo...

This article is about the city. For other uses, see Moquegua (disambiguation). City in PeruMoqueguaCityFrom the top: Main square, NorVill winery, View of Moquegua, 25 November stadium, Old matrix church and Santo Domingo complex FlagCoat of armsMoqueguaCoordinates: 17°12′S 70°56′W / 17.200°S 70.933°W / -17.200; -70.933Country PeruDepartmentMoqueguaProvinceMariscal NietoDistrictMoqueguaGovernment • MayorAbraham Alejandro Cárdenas Romero(2019-20...













































