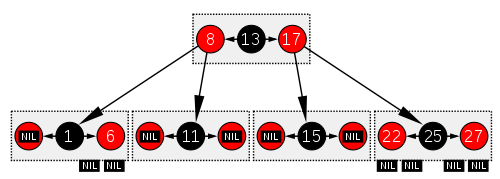
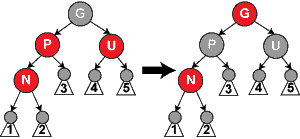
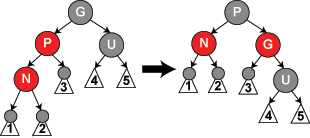
درخت سرخ-سیاه
| |||||||||||||||||||||||||||||||||||||
Read other articles:

2013 video gameKiller Is DeadNorth American cover artDeveloper(s)Grasshopper Manufacture[a]Publisher(s)PlayStation 3, Xbox 360JP: Kadokawa GamesNA: Xseed GamesPAL: Deep SilverWindowsDeep SilverDirector(s)Hideyuki ShinProducer(s)Yoshimi YasudaShuji IshikawaDesigner(s)Tadayuki NoumaruKees GajentaanHikaru TamadaArtist(s)Takashi KasaharaYusuke ItoWriter(s)Goichi SudaKeisuke MakinoYudai YamaguchiHideyuki ShinComposer(s)Akira YamaokaRyo KoikeYasuhiro IsodaKouta KannoEngineUnreal Engine 3Pla...

Torralba TuràlvaKomuneComune di TorralbaLokasi Torralba di Provinsi SassariNegara ItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan • Wali kotaVincenzo DoreLuas[1] • Total36,5 km2 (14,1 sq mi)Ketinggian[2]435 m (1,427 ft)Populasi (2016)[3] • Total974 • Kepadatan27/km2 (69/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos07048Kode area telepon079Si...

Arts centre, based in a church, in Wales Norwegian Church Arts CentreLocationCardiff BayCoordinates51°27′41″N 3°09′43″W / 51.46143°N 3.16192°W / 51.46143; -3.16192Built1868Original useLutheran ChurchCurrent useMuseum; Arts Centre; CafeVisitors180,000 (in 2018/19)[1]OwnerNorwegian Church Preservation TrustWebsitehttp://www.norwegianchurchcardiff.com The Norwegian Church Arts Centre (Welsh: Canolfan Gelfyddydau'r Eglwys Norwyaidd) is a point of c...

Para otros usos de este término, véase Tortura (desambiguación). Grabado probablemente del siglo XVI que muestra diversos procedimientos de tortura en un castillo de la actual Eslovaquia. A la izquierda, el toro de Falaris; al fondo la garrucha (junto al torturado el tribunal y el escribano que anotan todo lo que dice) y en primer plano el potro cuyo torno está siendo accionado por el verdugo (el hombre tumbado en el potro está siendo torturado también mediante el tormento del agua). La...

Questa voce sull'argomento cestisti giapponesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Rui Hachimura Hachimura con la maglia degli Washington Wizards Nazionalità Giappone Altezza 203 cm Peso 104 kg Pallacanestro Ruolo Ala grande Squadra L.A. Lakers Carriera Giovanili Meisei High School2016-2019 Gonzaga Bulldogs Squadre di club 2019-2023 Wash. Wizards177 (2.303)2023- L...

20. Eurovision Young Musicians Datum Abgesagtursprünglich geplant: 17.–21. Juni 2020 Austragungsland Kroatien Kroatien Austragungsort Halbfinale:Musikakademie, Zagreb Finale:König-Tomislav-Platz, Zagreb Austragender Fernsehsender Teilnehmende Länder 11 Zurückkehrende Teilnehmer Ukraine Ukraine Zurückgezogene Teilnehmer Albanien Albanien,Belgien Belgien,Israel Israel,Russland Russland,San Marino San Marino,Spanien Spanien,Ungarn Ungarn,Ver...

Юс — термін, який має кілька значень. Ця сторінка значень містить посилання на статті про кожне з них.Якщо ви потрапили сюди за внутрішнім посиланням, будь ласка, поверніться та виправте його так, щоб воно вказувало безпосередньо на потрібну статтю.@ пошук посилань саме с�...

Korban serangan asam di Kamboja Pelemparan asam, yang juga disebut serangan asam[1], serangan vitriol, vitriolase, atau serangan air keras, adalah sebuah bentuk dari serangan kekerasan[2][3][4] yang didefinisikan sebagai tindakan melempar asam atau bahan korosif serupa terhadap tubuh orang lain dengan tujuan menyakiti, melukai, menyiksa atau membunuh.[5] Para pelaku serangan tersebut melempar asam ke korban mereka, biasanya ke wajah mereka, membakar mer...

Swedish handball player (1915-2003) Curt Wadmark Curt Wadmark (pronounced [ˈkɵʈː ˈvɑ̂ːdmark]; 30 January 1915 – 21 July 2003)[1] was a Swedish handball player, coach and administrator. He played for IFK Lund during the club's only season in the top division in 1938–39.[2] At the end of the season the team withdrew from the league and Wadmark moved to IFK Kristianstad due to the lack of a venue for handball in Lund.[3] He helped the team to two secon...

Asian Youth Beach Handball ChampionshipCurrent season, competition or edition: 2022 Asian Youth Beach Handball ChampionshipSportBeach HandballFounded2015FounderAsian Handball FederationInaugural season2016No. of teams16 (maximum)ContinentAHF (Asia)Most recentchampion(s)Men – Thailand (1st Title) Women – China (1st Title)Most titlesMen – Thailand (1 Title) Women – China (1 Title)TV partner(s)Al Kass Sports ChannelsPromotion toIHF Youth Beach Handball World Champ...

Takut Ga Sih...Genre Drama Horor Komedi Skenario Messiah Fadjarwati[a] Deden Yuli Tristanto[b] Boim Lebon[c] Endik Koeswoyo[d] Erry Sofid[e] Sutradara Zoel Fadly[f] Reka Wijaya[g] Saad Bima[h] Chiska Doppert[i] Ali Pare[j] Pemeran Rendy Kjaernett Elgi Purnama Fachri Muhammad Valerie Tifanka Oded Kravitz Penggubah lagu temaNoahLagu pembukaSahabat — NoahLagu penutupSahabat — NoahPenata musikNicanoorsNegara...

British gastroenterologist This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (February 2017) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous...

Airport in East Java , IndonesiaAbdul Rachman Saleh AirportBandar UdaraAbdul Rachman SalehNew public terminal, 2015 airside viewOriginal public terminal in 2008IATA: MLGICAO: WARASummaryAirport typePublic / MilitaryOwnerGovernment of East Java ProvinceOperatorAngkasa PuraServesMalangLocationPakis, Malang, East Java 65154, IndonesiaBuilt1937; 86 years ago (1937)Time zoneWITA (UTC+07:00)Elevation AMSL526 m / 1,726 ftCoordinates07°55′42″S 112°42′48″E&#x...

Primero la música y luego las palabras Prima la musica e poi le parole Retrato de Antonio Salieri, óleo de 1825.Género divertimento teatraleActos 1 actoPublicaciónAño de publicación siglo XVIIIIdioma ItalianoMúsicaCompositor Antonio SalieriPuesta en escenaLugar de estreno Orangerie de Schönbrunn (Viena)Fecha de estreno 7 de febrero de 1786Personajes véase PersonajesLibretista Giovanni Battista Casti[editar datos en Wikidata] Prima la musica e poi le parole (título ori...

Serbian writer (1948–2023) David AlbahariAlbahari in 2011Born(1948-03-15)15 March 1948Peć, PR Serbia, FPR YugoslaviaDied30 July 2023(2023-07-30) (aged 75)Belgrade, SerbiaOccupationWriter, novelistNationalitySerbian, CanadianAlma materUniversity of Belgrade Faculty of PhilologyChildrenNatan Albahari Rebeka Albahari David Albahari (Serbian Cyrillic: Давид Албахари, pronounced [dǎv̞id albaxǎːriː]; 15 March 1948 – 30 July 2023) was a Serbian writer. Albaha...

Hamburger Admiralitätsflagge Die Hamburgische Admiralität – vollständiger Name: Hamburgisches Admiralitäts-Collegium – war von 1623 bis 1811 die wichtigste Hafenbehörde Hamburgs. Ihre Zuständigkeit umfasste nicht nur militärische, sondern auch richterliche und administrative Aufgaben, die später auf verschiedene andere Institutionen übergingen. Inhaltsverzeichnis 1 Geschichte 2 Wasserschout 3 Literatur 4 Siehe auch 5 Weblinks 6 Einzelnachweise Geschichte Admiralitätsya...

American sprinter David VerburgVerburg at the 2016 OlympicsPersonal informationNickname(s)Davy Crocket, SankaNationalityAmericanBorn (1991-05-14) May 14, 1991 (age 32)Oklahoma City, Oklahoma, U.S.EducationE. C. Glass High SchoolAlma materGeorge Mason UniversityHeight5 ft 6 in (168 cm)Weight154 lb (70 kg)SportCountry United StatesSportAthletics (track and field)Event(s)400 meters, 800 metersCollege teamGeorge Mason UniversityAchievements and titlesPerson...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Logisticus angustatus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Logisticus Spesies: Logisticus angustatus Logisticus angustatus adalah spesies kumbang tanduk panjang yang tergol...

Switzerland based biotechnology company This article needs to be updated. Please help update this article to reflect recent events or newly available information. (August 2017) Serono S.A.TypeS.AIndustryBiotechnologyPharmaceuticalFounded1906 (1906)FounderCesare SeronoDefunct2006; 17 years ago (2006)FateAcquired by Merck GroupSuccessorMerck SeronoHeadquartersGeneva, Switzerland (former Headquarters)Key peopleClaudio Bertarelli (Chairman)Ernesto Bertarelli (CEO)ProductsRe...

1994 single by Silverchair TomorrowUK singleSingle by Silverchairfrom the album Frogstomp B-sideBlind (live)Released16 September 1994Recorded1994StudioTriple J (Sydney, Australia)GenreGrunge[1][2]Length4:25Label Murmur Columbia Songwriter(s) Daniel Johns Ben Gillies Producer(s)Kevin ShirleySilverchair singles chronology Tomorrow (1994) Pure Massacre (1995) Tomorrow is a song by Australian rock band Silverchair, which was released on 16 September 1994 on their debut extended pl...