Término de corrección de Madhava
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Oil field in Utah, USA Squaw Canyon Oil Field is located in San Juan County, approximately 25 miles (40 km) southeast of Blanding, Utah. Production is from a northwest–southeast trending 20-foot-thick (6.1 m) carbonate buildup in the Pennsyslvanian Desert Creek. The field is part of the Paradox Basin that extends from the states of Colorado to Utah and New Mexico. Tin Cup Federal 1-35 Water Injection Well Reservoir is a carbonate phylloid algal lime wackestone to packstone. The fi...

Tras la terminación de las hostilidades en la Segunda Guerra Mundial, los Aliados tenían el control de los países derrotados del Eje. Anticipándose a la derrota de Alemania y Japón, ya habían creado la Comisión Asesora Europea y una propuesta Comisión Asesora del Lejano Oriente para hacer recomendaciones para el período de posguerra. En consecuencia, administraron su control de los países derrotados a través de Comisiones Aliadas, a menudo denominadas Comisiones de Control Aliadas ...

2019 Indian Punjabi-language comedy-drama film Chal Mera PuttTheatrical film posterDirected byJanjot SinghScreenplay byRakesh DhawanKulwant SinghStory byRakesh DhawanProduced byKaraj GillAshu Munish SahniStarringAmrinder GillSimi ChahalIftikhar ThakurNasir ChinyotiAkram UdasRup KhatkarHardeep GillGurshabadCinematographySandeep PatilEdited bySadik Ali ShaikhMusic byDr ZeusGurcharan SinghProductioncompaniesRhythm Boyz EntertainmentGillz NetworkOmjee Star StudiosDistributed byOmjee Star StudiosR...

Ambassador of Iran to the United Arab EmiratesCoat of Arms of IranIncumbentReza Amerisince June 15, 2023[1]Inaugural holderManuchehr BehnamFormationJanuary 18, 1973 The Iranian ambassador in Abu Dhabi is the official representative of the Government in Tehran to the Government of the United Arab Emirates. List of representatives Diplomatic accreditation Ambassador Persian language Observations List of presidents of Iran List of prime ministers of the United Arab Emirates Term end...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) رياضة باكو جاوي سنة 2015 باكو جاوي (بالجاوية:Pacu jawi)، هي مهرجان سنوي يقوم بالسباق التقليدي للثيران في تانار داتار، مقاطعة سومطرة الغربية، سومطرة، إندونيسيا، وهي
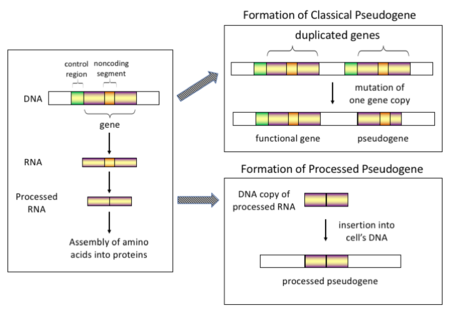
Pseudogen (Inggris; Pseudogenes) adalah salinan gen yang biasanya tidak memiliki intron dan urutan DNA, dan bisa juga diartikan sebagai segmen non-fungsional dari DNA yang menyerupai fungsional asli dari gen itu sendiri.[1] Meskipun pseudogen secara genetik terlihat mirip dengan gen fungsional asli, namun pseudogen sudah mengalami banyak mutasi. Sebagian besar pseudogen muncul sebagai salinan gen fungsional yang berlebihan, baik secara langsung oleh duplikasi DNA ataupun juga secara t...

State Legislative Assembly Constituency in Tamil Nadu SankarapuramConstituency for the Tamil Nadu Legislative AssemblyConstituency detailsCountryIndiaRegionSouth IndiaStateTamil NaduDistrictKallakurichiLS constituencyKallakurichiTotal electors2,68,535[1]Member of Legislative Assembly16th Tamil Nadu Legislative AssemblyIncumbent T. Udhayasuriyan Party DMKElected year2021 Sankarapuram is a state assembly constituency in kallakurichi district of Tamil Nadu, India.[2] I...

Franco-Moroccan actor, comedian and director Jamel DebbouzeDebbouze in 2016Born (1975-06-18) 18 June 1975 (age 48)Paris, FranceNationalityMoroccan, FrenchOccupation(s)Actor, comedian, screenwriter, film producer and directorYears active1992–presentSpouse Mélissa Theuriau (m. 2008)Children2Websitewww.jameldebbouze.fr Jamel Debbouze (French pronunciation: [dʒamɛl dəbuz]; Arabic: جمال دبوز, romanized: Jamāl Dabūz; born 18 June...

2011 television film directed by Patricia Riggen Lemonade MouthExtended edition US DVD coverGenre Drama Musical Based onLemonade Mouthby Mark Peter HughesTeleplay byApril BlairDirected byPatricia RiggenStarring Bridgit Mendler Adam Hicks Hayley Kiyoko Naomi Scott Blake Michael Music byChristopher LennertzCountry of originUnited StatesOriginal languageEnglishProductionExecutive producerDebra Martin ChaseProducerMatias AlvarezCinematographyChecco VareseEditorGirish BhargavaRunning time106 minut...

1981 film by Oz Scott & Michael Schultz Bustin' LooseTheatrical release poster for Bustin' Loose.Directed by Oz Scott Michael Schultz (uncredited) Written by Lonne Elder III Richard Pryor Roger L. Simon Produced by Michael S. Glick Richard Pryor Starring Richard Pryor Cicely Tyson Robert Christian George Coe Music by Mark Davis Roberta Flack Productioncompanies Omar Productions Northwest Film and Television Consultants Universal Clearances Distributed byUniversal PicturesRelease date May&...

Vleteren Gemeente in België (Details) Geografie Gewest Vlaanderen Provincie West-Vlaanderen Arrondissement Ieper Oppervlakte– Onbebouwd– Woongebied– Andere 38,58 km² (2021)89,6%3,92%6,48% Coördinaten 50° 56' NB, 2° 44' OL Bevolking (bron: Statbel) Inwoners– Mannen– Vrouwen– Bevolkingsdichtheid 3.611 (01/01/2023) 51,26% 48,74% 93,61 inw./km² Leeftijdsopbouw0-17 jaar18-64 jaar65 jaar en ouder (01/01/2023)21,32%58,32%20,35% Buitenlanders 2,99%...

Islamic concept of marriage Nikah and Nikaah redirect here. For the films, see Nikah (film) and Nikaah (film). Nikah process. The scene is set outside the Kilic Ali Pasha Mosque. (Turkey, 1837) A Pakistani bride signing a marriage certificate Part of a series onIslamic jurisprudence(fiqh) Ritual Shahada Salah Raka'ah Qibla Turbah Sunnah prayer (TahajjudTarawih) Witr Nafl prayer Sawm Zakat Hajj Ihram (clothing Mut'ah) Tawaf Umrah (and Hajj) Political Islamic leadership Caliphate Majl...

Car endurance race in Australia 2023 Bathurst 12 Hour Previous 2022 Next 2024 2023 Liqui-Moly Bathurst 12 HourEvent InformationDate3–5 February 2023LocationBathurst, New South WalesVenueMount Panorama CircuitResultsRace 1Distance laps kmPole position Maro EngelGruppeM Racing 2:00.8819 The 2023 Liqui Moly Bathurst 12 Hour was an endurance race for FIA GT3 cars and invited vehicles, staged at the Mount Panorama Circuit in Bathurst, New South Wales, Australia, on 5 February 2023. It was the op...

Resolusi 944Dewan Keamanan PBBPasukan yang datang ke Bandar Udara Internasional Toussaint Louverture pada hari pertama operasiTanggal29 September 1994Sidang no.3.430KodeS/RES/944 (Dokumen)TopikHaitiRingkasan hasil13 mendukungTidak ada menentang2 abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Argentina Brasil Republik Ceko Djibouti Spanyol Nigeria&...

Japanese multinational electronics and electrical equipment company This article needs to be updated. Please help update this article to reflect recent events or newly available information. (October 2018) Brother Industries, Ltd.Logo since 1982Brother Industries headquartersNative nameブラザー工業株式会社Romanized nameBurazā Kōgyō Kabushiki-gaishaTypePublicTraded asTYO: 6448IndustryPrinters, MachineryFounded1908; 115 years ago (1908) (as Yasui Sewing Machine Co...

2006 video gameGuild Wars NightfallDeveloper(s)ArenaNetPublisher(s)NCSOFTSeriesGuild WarsPlatform(s)WindowsReleaseNA: October 26, 2006 (retail)EU: October 27, 2006NA: April 22, 2009 (Steam)Genre(s)Action role-playing gameMode(s)Multiplayer Guild Wars Nightfall is a fantasy action role-playing game and the third stand-alone campaign in the Guild Wars series developed by ArenaNet, a subsidiary of NCSOFT corporation. Nightfall was released worldwide on October 27, 2006, having been in developmen...

American western drama television series The SonGenre Western Drama Based onThe Sonby Philipp MeyerDeveloped by Philipp Meyer Lee Shipman Brian McGreevy Starring Pierce Brosnan Henry Garrett Zahn McClarnon Jess Weixler Paola Núñez Elizabeth Frances Sydney Lucas Jacob Lofland David Wilson Barnes James Parks Shane Graham Kathryn Prescott Sean Alan Stone ComposerNathan BarrCountry of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes20 (list of episodes)ProductionExecuti...

New Fort Boise, 2018 Fort Boise is either of two different locations in the Western United States, both in southwestern Idaho. The first was a Hudson's Bay Company (HBC) trading post near the Snake River on what is now the Oregon border (in present-day Canyon County, Idaho), dating from the era when Idaho was included in the British fur company's Columbia District. After several rebuilds, the fort was ultimately abandoned in 1854, after it had become part of United States territory following ...

Pour les articles homonymes, voir Revizor. Le Revizor Le Revizor, couverture de la première édition (1836). Auteur Nicolas Gogol Genre Comédie Nb. d'actes 5 Dates d'écriture 1836 Version originale Titre original Ревизор Langue originale Russe Pays d'origine Empire russe Lieu de parution originale Saint-Pétersbourg Date de parution originale 1836 Date de création 1er mai 1836 Lieu de création Théâtre AlexandraSaint-Pétersbourg Version française Traducteur Eugène Moreau Date ...

Lake Lake RakshastalView South from Rakshas Tal Lake (2006)Lake RakshastalLocationTibet Autonomous Region,Coordinates30°39′N 81°15′E / 30.65°N 81.25°E / 30.65; 81.25 Lagngar CoChinese nameTraditional Chinese拉昂錯Simplified Chinese拉昂错TranscriptionsAlternative Chinese nameTraditional Chinese蘭嘎錯Simplified Chinese兰嘎错TranscriptionsStandard MandarinHanyu PinyinLángā cuòTibetan nameTibetanལག་ངར་མཚོTranscriptionsWyli...





















![{\displaystyle {\begin{aligned}&{\begin{aligned}{\frac {1}{p^{3}-p}}-{\frac {1}{(p+2)^{3}-(p+2)}}&<\left|{\frac {\pi }{4}}-s_{1}(n)\right|<{\frac {1}{p^{3}-p}},\\[10mu]{\frac {4}{p^{5}+4p}}-{\frac {4}{(p+2)^{5}+4(p+2)}}&<\left|{\frac {\pi }{4}}-s_{2}(n)\right|<{\frac {4}{p^{5}+4p}},\end{aligned}}\\[20mu]&{\begin{aligned}&{\frac {36}{p^{7}+7p^{5}+28p^{3}-36p}}-{\frac {36}{(p+2)^{7}+7(p+2)^{5}+28(p+2)^{3}-36(p+2)}}\cdots \\[10mu]&{\phantom {{\frac {4}{p^{5}+4p}}-{\frac {4}{(p+2)^{5}+4(p+2)}}}}<\left|{\frac {\pi }{4}}-s_{3}(n)\right|<{\frac {36}{p^{7}+7p^{5}+28p^{3}-36p}}.\end{aligned}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab3209ce7108dc0dc2434c27fe6de8587da7700e)































![{\displaystyle {\cfrac {1}{4n+{\cfrac {1^{2}}{n+{\cfrac {2^{2}}{4n+{\cfrac {3^{2}}{n+{\cfrac {\cdots }{\cdots +{\cfrac {r^{2}}{n[4-3(r{\bmod {2}})]+\cdots }}}}}}}}}}}}={\cfrac {1}{4n+{\cfrac {2^{2}}{4n+{\cfrac {4^{2}}{4n+{\cfrac {6^{2}}{4n+{\cfrac {8^{2}}{4n+\cdots }}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf3fa67d4fe78143c4c33bc7c55e952c1c600af5)







![{\displaystyle {\begin{alignedat}{3}S(1)&=\ \ \,{\frac {97}{452}}&&=\ \ \ {\frac {1}{4+{\frac {64}{97}}}}&&\approx {\frac {1}{4}},\\[6mu]S(2)&=\ \ {\frac {161}{1356}}&&=\ \ \,{\frac {1}{8+{\frac {68}{161}}}}&&\approx {\frac {1}{8}},\\[6mu]S(3)&=\ \ {\frac {551}{6780}}&&=\ \,{\frac {1}{12+{\frac {168}{551}}}}&&\approx {\frac {1}{12}},\\[6mu]S(4)&=\ {\frac {2923}{47460}}&&=\ {\frac {1}{16+{\frac {692}{2923}}}}&&\approx {\frac {1}{16}},\\[6mu]S(5)&={\frac {21153}{427140}}&&={\frac {1}{20+{\frac {4080}{21153}}}}&&\approx {\frac {1}{20}}.\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7fbd6561d4b7fa2ce6bb1ff9ad14498c57107de)


![{\displaystyle {\begin{alignedat}{5}{\frac {64}{97}}&=\ \,{\frac {1}{1+{\frac {33}{64}}}}&&\approx {\frac {1}{1}},&{\frac {33}{64}}&=\,{\frac {1}{1+{\frac {31}{33}}}}&&\approx {\frac {1}{1}},\\[6mu]{\frac {68}{161}}&=\ \,{\frac {1}{2+{\frac {25}{68}}}}&&\approx {\frac {1}{2}},&{\frac {25}{68}}&=\,{\frac {1}{2+{\frac {18}{25}}}}&&\approx {\frac {1}{2}},\\[6mu]{\frac {168}{551}}&=\ {\frac {1}{3+{\frac {47}{168}}}}&&\approx {\frac {1}{3}},&{\frac {47}{168}}&=\,{\frac {1}{3+{\frac {27}{47}}}}&&\approx {\frac {1}{3}},\\[6mu]{\frac {692}{2923}}&={\frac {1}{4+{\frac {155}{692}}}}&&\approx {\frac {1}{4}},&{\frac {155}{692}}&={\frac {1}{4+{\frac {72}{155}}}}&&\approx {\frac {1}{4}},\\[6mu]{\frac {4080}{21153}}&={\frac {1}{5+{\frac {753}{4080}}}}&&\approx {\frac {1}{5}},&\quad {\frac {753}{4080}}&={\frac {1}{5+{\frac {315}{753}}}}&&\approx {\frac {1}{5}}.\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de52d69cacd6e9cf3f64ae7811d5cc6d33e69337)




