François Viète
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:
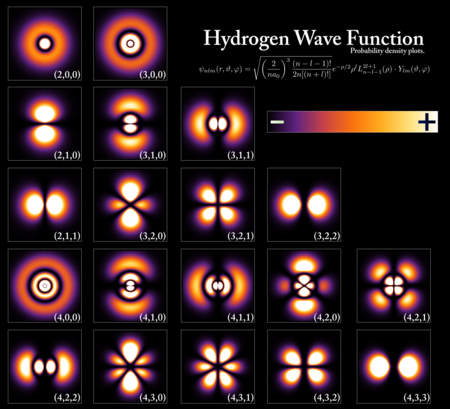
Untuk artikel pendahuluan, lihat Pengantar mekanika kuantum. Bagian dari seri artikel mengenaiMekanika kuantum H ^ | ψ ( t ) ⟩ = i ℏ ∂ ∂ t | ψ ( t ) ⟩ {\displaystyle {\hat {H}}|\psi (t)\rangle =i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle } Persamaan Schrödinger Pengantar Glosarium Sejarah Buku teks Latar belakang Mekanika klasik Teori kuantum lama Notasi Bra–ket Hamiltonian Interferensi Dasar-dasar Bilangan kuantum Dekohere...

تشمل حركة القداسة مجموعة من المعتقدات والشعائرالمسيحية التي نشأت في المذهب الميثودي في القرن التاسع عشر نشوءها الأكبر، وإلى درجة أقل في مذاهب أخرى كمذهب جمعية الأصدقاء وتجديدية العماد. الحركة ويسليانية أرمينيانية في لاهوتها، ويميزها تركيزها على عقيدة عمل النعمة الثاني،...

Bagian dari seri tentangHukum KanonikGereja Katolik Hukum Mutakhir Kitab Hukum Kanonik 1983 Omnium in mentem Kitab Hukum Kanon Gereja-Gereja Timur Ad tuendam fidem Ex Corde Ecclesiae Indulgentiarum Doctrina Pastor Bonus Pontificalis Domus Universi Dominici Gregis Consuetudo Sejarah Hukum Kitab Hukum Kanonik 1917 Corpus Iuris Canonici Dekretis Regulæ Iuris Decretales Gregorii IX Dekretalis Decretum Gratiani Extravagantes Liber Septimus Tata Tertib Gereja Purba Didakhe Konstitusi Apostolik Kan...

Йоганн Діханіх Йоганн Діханіх Особисті дані Народження 16 листопада 1956(1956-11-16) (67 років) Айзенштадт, Австрія Зріст 174 см Вага 65 кг Громадянство Австрія Позиція півзахисник Інформація про клуб Поточний клуб завершив кар'єру Професіональні клуби* Роки Клуб І (г) 1978

Der Titel dieses Artikels ist mehrdeutig. Zum württembergischen und kurhannoverschen Verwaltungsbeamten siehe Johann Friedrich von Staffhorst. Wappen Deutschlandkarte 52.7216666666678.979722222222247Koordinaten: 52° 43′ N, 8° 59′ O Basisdaten Bundesland: Niedersachsen Landkreis: Diepholz Samtgemeinde: Siedenburg Höhe: 47 m ü. NHN Fläche: 14,65 km2 Einwohner: 517 (31. Dez. 2022)[1] Bevölkerungsdichte: 35 Einwohner je km2 ...

بيبل غوتنبرغ، أول طبعة للكتاب المقدس، طبعها يوهان غوتنبرغ، وله أهمية كبيرة في بدء ثورة وعصر الطباعة. الأدب المسيحي مصطلح يشير للمواضيع أو التقاليد الأدبية المسيحية. كان الأدب أحد المجالات الثقافية البارزة التي أثرت بها المسيحية. مع التقليد الأدبي الذي يمتد ألفي سنة، كانت ا

St. Paulus (Schüller) Die Kirche St. Paulus ist die römisch-katholische Kirche von Schüller im Landkreis Vulkaneifel in Rheinland-Pfalz. Die Filialkirche gehört in der Pfarreiengemeinschaft Obere Kyll zum Pastoralen Raum Adenau-Gerolstein im Bistum Trier. Inhaltsverzeichnis 1 Geschichte 2 Ausstattung 3 Literatur 4 Weblinks Geschichte Der Architekt Franz Statz baute von 1910 bis 1911 die heutige Kirche von Schüller. Sie ist dem Apostel Paulus geweiht. Der neugotische Bau ist eine dreischi...

Puti bungsu menurut cerita rakyat Sumatera Barat merupakan salah seorang dari istri raja Puti Bungsu merupakan nama tokoh yang ditemui dalam cerita rakyat Minang Kabau Sumatera Barat.[1] Puti bungsu menurut cerita rakyat setempat ialah satu dari tujuh putri yang datang dari langit.[1] Puti Bungsu merupakan tokoh wanita yang hidup dalam cerita rakyat.[1] Puti bungsu dalam cerita rakyat Sumatera Barat selain disebut sebagai putri yang turun dari langit juga disebut sebag...

Radio station in Texarkana, TexasKTFSTexarkana, TexasFrequency940 kHzBrandingKTOY Gospel 105.9 (Christmas 105.9)ProgrammingFormatUrban Gospel (Christmas Music)OwnershipOwnerCliff Dumas(BTC USA Holdings Management Inc.)Sister stationsKBYB, KCMC, KTFS-FM, KTOY, KTTYHistoryFirst air date1961; 62 years ago (1961)Former call signsKADO (1961-1989)KTWN (1989-1996)KTFS (1996-2014)KCMC (2014-2017)Technical information[1]Licensing authorityFCCFacility ID33542ClassDPower2,500 w...

Joachim Camerarius der Jüngere Joachim Camerarius der Jüngere, auch Joachim Cammermeister (* 6. November 1534 in Nürnberg; † 11. Oktober 1598 ebenda) war ein deutscher Arzt, Botaniker und Naturforscher. Ludwig Camerarius war sein Sohn. Inhaltsverzeichnis 1 Leben und Wirken 2 Schriften (Auswahl) 3 Literatur 4 Weblinks 5 Einzelnachweise Leben und Wirken Der Sohn von Joachim Camerarius dem Älteren besuchte das Gymnasium Schulpforta. Er studierte Medizin an der Universität Wittenberg, wo e...

Turkish militia leader (1886–1948) EfeÇerkes EthemBeyBorn1886 (1886)Bandırma, Hüdavendigâr Vilayet, Ottoman Empire (present-day Balıkesir, Turkey)DiedSeptember 21, 1948(1948-09-21) (aged 61–62)Amman, JordanBuriedCemetery of Habjouka in Al-Misdar, Amman, JordanAllegianceOttoman Empire (1900-1919)Ankara Government (1919-1920)Service/branchKuva-yi SeyyareBattles/warsBalkan WarsWorld War ITurkish War of Independence Greco-Turkish War (1919-1922) Revolt of Ahmet Anzavur Alma mat...

Pour les articles homonymes, voir The Square. The Square Données clés Réalisation Ruben Östlund Scénario Ruben Östlund Acteurs principaux Claes Bang Elisabeth Moss Dominic West Terry Notary Sociétés de production Plattform Produktion Pays de production Suède Allemagne France Danemark Genre Comédie dramatique Durée 142 minutes Sortie 2017 Pour plus de détails, voir Fiche technique et Distribution The Square est une comédie dramatique suédo-germano-dano-française, écrite et réa...

Chemical compound NetoglitazoneClinical dataATC codeNoneIdentifiers IUPAC name 5-[(6-[(2-Fluorophenyl)methoxy]naphthalen-2-yl)methyl]-1,3-thiazolidine-2,4-dione CAS Number161600-01-7 YPubChem CID204109IUPHAR/BPS2707DrugBankDB09199ChemSpider176806 NUNIIQOV2JZ647AKEGGD05150 YCompTox Dashboard (EPA)DTXSID5043712 ECHA InfoCard100.233.314 Chemical and physical dataFormulaC21H16FNO3SMolar mass381.42 g·mol−13D model (JSmol)Interactive image SMILES C1=CC=C(C(=C1)COC2=CC3=C(C=C2...

Spanish footballer (born 1990) For the Mexican violinist, conductor and composer, see Daniel Ayala Pérez. For the Chilean handball player, see Daniel Ayala (handballer). In this Spanish name, the first or paternal surname is Sánchez and the second or maternal family name is Ayala. Daniel Ayala Ayala training with Liverpool in 2011Personal informationFull name Daniel Sánchez Ayala[1]Date of birth (1990-11-07) 7 November 1990 (age 33)Place of birth El Saucejo, SpainHeigh...

Species of flowering plant Melaleuca parvistaminea In Morton National Park Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Myrtales Family: Myrtaceae Genus: Melaleuca Species: M. parvistaminea Binomial name Melaleuca parvistamineaByrnes[1] Melaleuca parvistaminea is a plant in the myrtle family, Myrtaceae, and is endemic to the states of New South Wales and Victoria in Australia. It has hard, rough bark, crea...

Karl VAdipati LorraineKelahiran(1643-04-03)3 April 1643Wina, AustriaKematian18 April 1690(1690-04-18) (umur 47)Wels, AustriaWangsaLorraineNama lengkapCharles Léopold Nicolas Sixte de LorraineAyahNicolas François, Adipati LorraineIbuClaude Françoise dari LorrainePasanganEleanor dari AustriaAnakLeopold, Adipati LorraineKarl Josef, Uskup OlomoucFrançois, Kepala Biara Malmedy Karl V (Charles Léopold Nicolas Sixte; 3 April 1643 – 18 April 1690) adalah seorang negarawan Aus...

Norman earl (c. 1011–2022) The Earl of HerefordCoat of arms of William FitzOsbernBornc. 1011Died22 February 1071(1071-02-22) (aged 60–61)FlandersCause of deathWarKnown for Lord of Breteuil Earl of Hereford companion of William the Conqueror TitleThe Earl of Hereford Lord of BreteuilSpouseAdeliza de TosnyChildren William of Breteuil Roger de Breteuil Emma de Breteuil Parent(s)Osbern the Steward and Emma of IvryRelatives Rodulf of Ivry (maternal grandfather) Osbern FitzOsbern...

Peta yang menunjukkan negara-negara anggota Liga Arab (hijau) dan Uni Eropa (jingga). Hubungan Liga Arab dengan Uni Eropa adalah hubungan bilateral antara dua organisasi regional antara Liga Arab (organisasi yang menaungi negara-negara Arab) dengan Uni Eropa (organisasi regional yang menaungi negara-negara Eropa). Kedua organisasi melakukan hubungan kerjasama untuk berbagai kepentingan kawasan masing-masing, baik dalam bidang pertahanan, keamanan, ekonomi, politik, dan budaya.[1] Seja...

1982 single by Frank and Moon ZappaValley GirlSingle by Frank and Moon Zappafrom the album Ship Arriving Too Late to Save a Drowning Witch B-sideYou Are What You IsReleasedJune 1982Recorded1982Genre Comedy rock new wave novelty Length4:59 (album version)3:47 (single version)LabelBarking Pumpkin, CBSSongwriter(s) Frank Zappa Moon Zappa Producer(s)Frank ZappaFrank Zappa singles chronology Goblin Girl (1981) Valley Girl (1982) The Man from Utopia Meets Mary Lou (1983) Valley Girl is a song b...

This article is about the district. For its eponymous headquarters, see Udaipur. District of Rajasthan in IndiaUdaipur districtDistrict of RajasthanClockwise from top-left: View of Udaipur from City Palace, Jaisamand Lake, Ghats at Udaipur, Aravalli Hills, Jagdhish TempleLocation of Udaipur district in RajasthanCoordinates (Udaipur): 24°23′N 73°37′E / 24.383°N 73.617°E / 24.383; 73.617Country IndiaStateRajasthanDivisionUdaipurHeadquartersUdaipurTehsils...