Grafo de Turán
| ||||||||||||||||||||||||||||
Read other articles:

1950 film by Andrew Marton, Compton Bennett King Solomon's MinesPromotional film posterDirected byCompton BennettAndrew MartonScreenplay byHelen DeutschBased onKing Solomon's Mines1885 novelby H. Rider HaggardProduced bySam ZimbalistStarringDeborah KerrStewart GrangerRichard CarlsonCinematographyRobert SurteesEdited byRalph E. WintersConrad A. NervigMusic byMischa SpolianskyProductioncompanyMetro-Goldwyn-MayerDistributed byLoew's, IncRelease dates November 9, 1950 (1950-11-09)&...

Hitung mundur waktu pembukaan kejuaraan di (Lviv, Ukraine) Proses pemilihan tuan rumah untuk Kejuaraan Eropa UEFA 2012 berakhir pada 18 April 2007 ketika penawaran bersama antara Polandia-Ukraina terpilih menjadi tuan rumah. Sejarah Saat awal dibukanya pendaftaran untuk penmilihan tuan rumah kejuaraan, ada lima penawaran yang masuk mewakili tujuh negara yaitu: Kroasia-Hungaria (tuan rumah bersama), Yunani, Italia, Polandia-Ukraina (tuan rumah bersama) dan Turki. Pada 8 November 2005, komite E...

Copper manganese silicate mineral AbswurmbachiteGeneralCategoryNesosilicateFormula(repeating unit)(Cu,Mn2+)Mn3+6O8SiO4IMA symbolAbs[1]Strunz classification9.AG.05Dana classification7.5.1.4Crystal systemTetragonalCrystal class4/mmm - Ditetragonal dipyramidalIdentificationColorBlackCleavageNoneTenacityBrittleMohs scale hardness6.5LusterMetallicStreakBrownish blackSpecific gravity4.96 g/cm3Density4.96 g/cm3Common impuritiesIronReferences[2] Abswurmbachite is a copper manganese si...

China National Petroleum Corporation中国石油天然气集团公司Pusat CNPCJenisPerusahaan pemerintahIndustriMinyak bumi dan gas alamDidirikan1988 (1988)KantorpusatDistrik Dongcheng, Beijing, Republik Rakyat TiongkokTokohkunciZhou Jiping (Chairman)Kosong (Presiden)ProdukMinyak bumi, gas alam dan petrokimia lainPendapatan US$ 432.000 miliar (2014)[1]Laba bersih US$ 16.317 miliar (2011)[1]Total aset US$ 481.07 miliar (2011)[1]Total ekuitas US$ 240.53 miliar (201...

This is a comprehensive list of the most noteworthy and tallest buildings in Albania.[1][2] Skyscrapers List of buildings with a minimum height of 100 m (330 ft). No. Name Image Location Height Floors Architect Developer Year 1 Mount Tirana Tirana41°19′48″N 19°49′14″E / 41.3299301°N 19.8205339°E / 41.3299301; 19.8205339 205 m (673 ft)[3] 58 CEBRA Nova Construction Sh.p.k u/c 2 Bofill Tower Tirana –[4] 58...

Sebuah bangunan hotel Four Points by Sheraton Four Points by Sheraton merupakan sebuah merek hotel mid-market dari Marriott International. Jaringan hotel ini diusung sebagai versi ekonomi dari Hotel Sheraton, dan formasi awalnya dibentuk dari rebranding hotel-hotel dengan nama Sheraton Inn. Seperti Hotel Sheraton, Four Points dimiliki oleh perusahaan ITT Sheraton, sebelum diambil alih oleh Starwood Hotels & Resorts pada 1998. Pada tahun 2016, Marriott International membeli Starwood, menja...

WiiWarePengembangNintendoTipePasar mayaTanggal diluncurkanWii25 Maret 2008Wii U18 November 2012PlatformWii, Wii U WiiWare adalah sebuah layanan yang membolehkan para pemakai Wii untuk mengunduh permainan dan aplikasi yang khusus dirancang dan dikembangkan untuk konsol permainan video Wii yang dibuat oleh Nintendo. Permainan dan aplikasi tersebut hanya dapat dibeli dan diunduh dari Wii Shop Channel di bawah naungan WiiWare. Saat pemakai mengunduh permainan atau aplikasi, ini akan tampak dalam ...

Floating restaurant boat The MS Normac in Toronto Harbour History Canada Name James R. Elliot (1902-1930) Normac (1930-present) Owner Detroit Fire Department (1902-1930) Owen Sound Transportation (1930-1968) Don Lee (1968-1969) John Letnik (1969-present) BuilderJenks Shipbuilding Company, Port Huron, Michigan Launched29 November 1902 Out of service1969 StatusVacant former restaurant ship moored at Port Dalhousie Pier Marina General characteristics TypeSteamship Tonnage210 GRT Length110 ft Bea...

Parade in Toronto, Ontario, Canada Toronto Santa Claus ParadeSanta at the 2010 Toronto Santa Claus ParadeStatusActiveGenreChristmas paradeFrequencyAnnually in NovemberLocation(s)Toronto, OntarioYears active1905–presentWebsitethesantaclausparade.com The Toronto Santa Claus Parade, also branded as The Original Santa Claus Parade, is a Santa Claus parade held annually in Toronto, Ontario, Canada. The 2023 event was held on November 26.[1] First held in 1905, it is one of the largest pa...

Public high school in Wallingford, Pennsylvania , United StatesStrath Haven High SchoolAddress205 S Providence RdWallingford, Pennsylvania 19086United StatesInformationTypePublic high schoolEstablished1983School districtWallingford-Swarthmore School DistrictPrincipalGreg HildenFaculty85.87 (FTE)[1]Grades9th – 12thNumber of students1,173 (2018–19)[1]Student to teacher ratio13.66[1]Color(s) Black Silver WhiteTeam namePanthersFeeder schoolsStrath H...

George Elnadus SupitAsisten Teritorial Panglima TNIMasa jabatan24 September 2018 – 27 Juli 2020PendahuluKustanto WidiatmokoPenggantiMadsuniPanglima Komando Daerah Militer XVII/CenderawasihMasa jabatan25 April 2017 – 24 September 2018PendahuluHinsa SiburianPenggantiYosua Pandit SembiringAsisten Operasi KasadMasa jabatan9 Juni 2016 – 25 April 2017PendahuluJohny L. TobingPenggantiSudirmanKepala Staf Komando Daerah Militer VI/MulawarmanMasa jabatan19 Januari 2015&...

Village in Kolubara District, SerbiaTvrdojevacVillage (Selo)TvrdojevacCoordinates: 44°25′N 19°59′E / 44.417°N 19.983°E / 44.417; 19.983Country SerbiaDistrictKolubara DistrictMunicipalityUbArea • Total8.56 km2 (3.31 sq mi)Elevation107 m (351 ft)Population (2011) • Total323 • Density38/km2 (98/sq mi)Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Tvrdojevac is a village in the...

Office skyscraper in Manhattan, New York DuMont BuildingGeneral informationLocation515 Madison Avenue, Manhattan, New York CityCoordinates40°45′36″N 73°58′26″W / 40.759897°N 73.973935°W / 40.759897; -73.973935Completed1931OwnerNewmark & Co.ManagementNewmark & Co.HeightTop floor162 m (531 ft)Technical detailsFloor count42[1]Floor area250,000 sq ft (23,000 m2)Design and constructionArchitect(s)J.E.R. CarpenterDeveloper...

Este artículo o sección tiene referencias, pero necesita más para complementar su verificabilidad.Este aviso fue puesto el 30 de junio de 2018. Igor Vovkovinskiy Igor Vovkovinskiy en 2013Información personalNombre nativo Ігор ВовковинськийNacimiento 18 de septiembre de 1982Bar, Óblast de Vínnytsia, RSS de Ucrania, Unión SoviéticaFallecimiento 20 de agosto de 2021 (38 años)Rochester, Minnesota, Estados UnidosCausa de muerte Afección cardiovascularNacionalidad ucrania...

Mixture of two or more immiscible liquids This article is about mixtures of liquids. For the light-sensitive mixture used in photography, see Photographic emulsion. Two immiscible liquids, not yet emulsifiedAn emulsion of Phase II dispersed in Phase IThe unstable emulsion progressively separatesThe surfactant (outline around particles) positions itself on the interfaces between Phase II and Phase I, stabilizing the emulsion An emulsion is a mixture of two or more liquids that are normally imm...
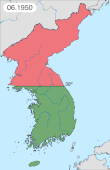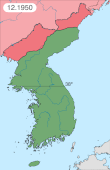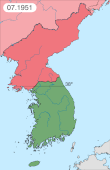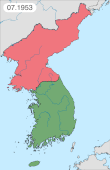
1950 Korean War battle 39°58′20″N 125°48′12″E / 39.97222°N 125.80333°E / 39.97222; 125.80333 (Unsan) Battle of UnsanPart of the Korean WarMap of Battle of Unsan on the night of 1 – 2 November 1950Date25 October – 4 November 1950LocationUnsan, North KoreaResult Chinese victoryBelligerents China United Nations United States South KoreaCommanders and leaders Peng Dehuai Wu Xinquan[1] Wen Yucheng[1] Frank W. M...

Logotipo da Valve Corporation Esta é a lista de jogos eletrônicos da Valve Corporation, uma desenvolvedora e publicadora de jogos eletrônicos norte-americana fundada em 1996 por Gabe Newell e Mike Harrington. A empresa está atualmente sediada em Bellevue, Washington.[1] O primeiro trabalho desenvolvido pela Valve foi Half-Life, um jogo de tiro em primeira pessoa lançado em 1998.[2] Tal jogo recebeu aclamação universal e vendeu mais de 9 milhões de unidades no varejo.[3][4] Com o lanç...

Residential home in Blackheath, LondonMorden CollegeTypeResidential homeLocationBlackheath, LondonCoordinates51°28′10″N 0°01′10″E / 51.4695°N 0.0195°E / 51.4695; 0.0195Built1695-1702ArchitectChristopher WrenGoverning bodyCharity Listed Building – Grade IOfficial nameMorden CollegeDesignated19 October 1951Reference no.1289879 Location of Morden College in Greater London Morden College is a charity which has been providing residential care in Blackheat...

1994 studio album by ErasureI Say I Say I SayStudio album by ErasureReleased16 May 1994[1]Recorded1993StudioStudio 142, The Church (London), Windmill Lane (Dublin), 37B (Chertsey, Surrey)[2][3]Genre Synth-pop dance Length44:08Label Mute (UK) Elektra (US) ProducerMartyn WareErasure chronology Chorus(1991) I Say I Say I Say(1994) Erasure(1995) Singles from I Say I Say I Say AlwaysReleased: 11 April 1994 Run to the SunReleased: 18 July 1994 I Love SaturdayReleased...

German army division during World War II 19th Panzer Division19. Panzer-DivisionUnit insigniaActive1 November 1940 – 8 May 1945Country GermanyBranchArmyTypePanzerRoleArmoured warfareSizeDivisionGarrison/HQWehrkreis XI: HanoverEngagementsWorld War II Operation Barbarossa Battle of Moscow Battle of Kursk Kamenets-Podolsky pocket Warsaw Uprising Vistula-Oder Offensive Prague Offensive Military unit The 19th Panzer Division (English: 19th Tank Division) was an armoured division in the Germ...