Espectro multifractal
|
Read other articles:

Tutmosis IV Faraón de la Dinastía XVIII de Egipto Reinado c. 1417 a 1407 a. CPredecesor Amenofis IISucesor Amenofis IIIInformación personalSepultura Tumba KV43, Valle de los Reyes, EgiptoFamiliaPadre Amenofis IIMadre TiaaConsorte Mutemuia, Iaret y Nefertari[editar datos en Wikidata] Menjeperura Thutmose,[1] Thutmose IV,[2] o Tutmosis IV,[3] es el octavo faraón de la dinastía XVIII de Egipto. Su reinado fue en torno a los años 1417 a 1407 a. C.[4]...

Cinema of Egypt List of Egyptian films Pre 1920 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 19941995 1996 1997 1998 1999 2000s 200...
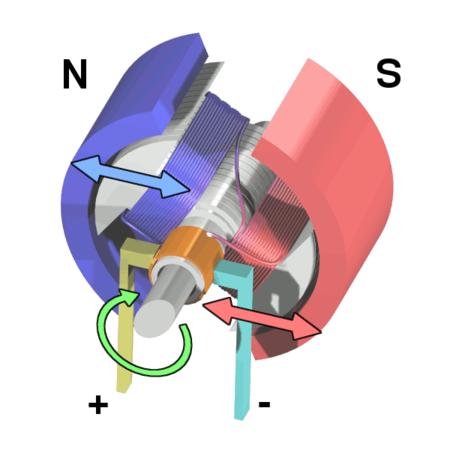
Gráfico de un motor de magnetización permanente. Un motor de imán permanente es un tipo de motor eléctrico del tipo paso a paso. Se lo conoce también como PMSM (permanent magnet synchronous motor). Son extensivamente usados en servomotores, accionamientos eléctricos para posicionamiento, robótica, máquinas herramienta, ascensores, etc. Estos motores suelen funcionar con dos imanes y en el centro se suele poner el motor y esto hace que se giren tras la atracción de los polos magnétic...

Pieza de código de un módulo del kernel de Linux, que utiliza snake case para los identificadores. Snake case se refiere al estilo de escritura en el que cada espacio se reemplaza con un carácter de subrayado (snake_case) y la primera letra de cada palabra se escribe en minúsculas. Es una convención de nomenclatura comúnmente usada en informática, por ejemplo, para nombres de variables y subrutinas, y para nombres de archivos . Un estudio encontró que los lectores pueden reconocer los...

Cet article est une ébauche concernant un parc national. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Parc national Körös-MarosConfluence entre le Körös et le Maros.GéographiePays HongrieCoordonnées 46° 34′ 23″ N, 21° 07′ 02″ ESuperficie 501,34 km2AdministrationType National park (d)Catégorie UICN V (paysage terrestre ou marin protégé)WDPA 178326Création ...

Halaman ini berisi artikel tentang surat kabar. Untuk kegunaan lain, lihat Hürriyet (disambiguasi). HürriyetBerkas:Hurriyetlogo.pngBerkas:Hürriyet ilk sayi.jpgKeluaran pertama, tertanggal 1 Mei 1948.TipeSurat kabar harianFormatBerliner (Lembar lebar sebelum 15 Oktober 2012)PemilikDoğan Media GroupRedaksiSedat ErginDidirikan1948Pandangan politikMainstreamLiberalismeSekulerisme[1]Tengah-KiriBahasaTurkiPusatGüneşli, Bağcılar, Istanbul, TurkiSirkulasi surat kabar 384,807 (12–18 ...

LayoverAlbum studio karya VDirilis8 September 2023 (2023-09-08)Durasi17:36LabelBig Hit Layover (ditulis sebagai Layo(v)er) adalah album studio debut dari penyanyi Korea Selatan V of BTS. Album ini dijadwalkan akan dirilis pada tanggal 8 September 2023, melalui Big Hit Music. Musik dan lirik Video musik Pada tanggal 10 Agustus 2023, video musik resmi untuk lagu Love Me Again dirilis.[1][2] Daftar lagu Daftar lagu LayoverNo.JudulDurasi1.Rainy Days2:592.Blue2:293.Love Me...

State electoral district of Victoria, Australia CranbourneVictoria—Legislative AssemblyLocation of Cranbourne (dark green) in Greater MelbourneStateVictoriaCreated1992; 31 years ago (1992)MPPauline RichardsPartyLabor PartyNamesakeCranbourne, VictoriaElectors61,814 (2018)Area63 km2 (24.3 sq mi)DemographicOuter metropolitan Electorates around Cranbourne: Carrum Narre Warren South Berwick Carrum Cranbourne Hastings Bass Bass Cranbourne is an electoral dist...

A cnidariologist is a zoologist specializing in Cnidaria. Examples Browne, Edward Thomas (1866–1937) Bigelow, Henry Bryant (1879–1967) Kirkpatrick, Randolph (1863–1950) Kishinouye, Kamakichi (1867–1929) Kramp, Paul Lassenius (1887–1975) Mayer, Alfred G. (1868–1922) References External links Wikispecies has information related to Category:Cnidariologists. vteExtant Cnidaria classesAnthozoa Octocorallia Hexacorallia Ceriantharia Medusozoa Cubozoa (box jellyfish) Hydrozoa (hydrozoans...

Cruiser of the Royal Navy For other ships with the same name, see HMS Leviathan. Leviathan at anchor History United Kingdom NameLeviathan NamesakeLeviathan BuilderJohn Brown & Company, Clydebank Laid down30 November 1899 Launched3 July 1901 Completed16 June 1903 FateSold for scrap, 3 March 1920 General characteristics Class and typeDrake-class armoured cruiser Displacement14,150 long tons (14,380 t) (normal) Length533 ft 6 in (162.6 m) (o/a) Beam71 ft 4 in (2...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bogotá Savannah Railway – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to remove this template message) Central Station of the Savannah Railway in 2010 The Bogotá Savannah Railway was a company that provided transport for passengers from 188...

Cricket team NigeriaOne Day nameJunior Yellow Greens[1]PersonnelCaptainSylvester OkpeCoachUthe Ogbimi The Nigeria Under-19 cricket team represents Nigeria in Under-19 cricket at the international level. It took part in the 2020 Under-19 Cricket World Cup qualification ICC Africa Division One tournament, held in Namibia. Nigeria defeated pre-tournament favourites Namibia by 52 runs,[2][3] Uganda by 30 runs and Kenya by 58 runs.[4][5] Nigeria won the tour...

Hefei 合肥Ho-fei, Luzhou, LuchowKota setingkat prefektur合肥市Gedung pencakar langit di HefeiLokasi prefektur Hefei, AnhuiNegaraTiongkokProvinsiAnhuiDivisi County7Pemerintahan • CPC Committee SecretaryWu Cunrong (吴存荣) • Wali kotaZhang Qingjun (张庆军)Luas • Kota setingkat prefektur7.029,48 km2 (271,410 sq mi) • Luas perkotaan838,5 km2 (3,237 sq mi) • Luas metropolitan838,5 km2 (3,237&#...

Tissue engineering researcher Nina TandonTandon at #EMCWorld in 2014BornNina Marie TandonEducationMBA, Columbia UniversityPhD in Biomedical Engineering, Columbia University, 2009MS in Electrical Engineering, MIT, 2006Bachelor of Electrical Engineering, Cooper Union, 2001OccupationsBiomedical engineerbusinesspersonauthorTitleCEO of EpiBone Nina Marie Tandon[1] is an American biomedical engineer. She is the CEO and co-founder of EpiBone.[2] She currently serves as an adjunct pro...

Church in West Virginia, United StatesRomney Presbyterian ChurchSouthern elevation facing Rosemary LaneRomney Presbyterian ChurchRomney Presbyterian ChurchShow map of Romney, West VirginiaRomney Presbyterian ChurchRomney Presbyterian Church (Eastern Panhandle of West Virginia)Show map of Eastern Panhandle of West VirginiaRomney Presbyterian ChurchRomney Presbyterian Church (West Virginia)Show map of West VirginiaRomney Presbyterian ChurchRomney Presbyterian Church (the United States)Show map ...

Цей розділ потрібно повністю переписати відповідно до стандартів якості Вікіпедії. Ви можете допомогти, переробивши його. Можливо, сторінка обговорення містить зауваження щодо потрібних змін. (жовтень 2011) Ґрунтовий покрив Полтавської області У ґрунтовому покриві Пол...

Halaman ini berisi artikel tentang aktor. Untuk pelawak, lihat Kartolo (pelawak). KartoloKartolo dan cellonya, circa 1941LahirYogyakarta, Hindia BelandaMeninggal18 Januari 1949Yogyakarta, IndonesiaPekerjaanAktor, penulis laguTahun aktif1930an–1948Karya terkenalTerang BoelanSuami/istriRoekiah (1933-1945; kematiannya) Raden Mas Kartolo (meninggal 18 Januari 1949) adalah aktor dan penulis lagu Indonesia. Ia dilahirkan di Yogyakarta dari keluarga bangsawan, ia berkecimpung dalam dunia teat...

Explosive charge to clear obstacles This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bangalore torpedo – news · newspapers · books · scholar · JSTOR (October 2007) (Learn how and when to remove this template message) Bangalore torpedo TypeExplosive chargePlace of originBritish IndiaService historyIn...

Supreme Court of the United States38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444EstablishedMarch 4, 1789; 234 years ago (1789-03-04)LocationWashington, D.C.Coordinates38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444Composition methodPresidential nomination with Senate confirmationAuthorized byConstitution of the United States, Art. III, § 1Judge term lengthli...

Not to be confused with In da Getto or In the Ghetto. 1996 single by David Morales & The Bad Yard Club featuring Crystal Waters & DeltaIn de Ghetto '96Single by David Morales & The Bad Yard Club featuring Crystal Waters & DeltaReleased1996 (1996)Genre House deep house Length2:54Label Manifesto Songwriter(s) David Morales Delta Bennett Handel Tucker Lowell Dunbar Producer(s)David Morales Handel Tucker Lowell Dunbar Crystal Waters singles chronology Relax(1995) In de Ghetto...





















