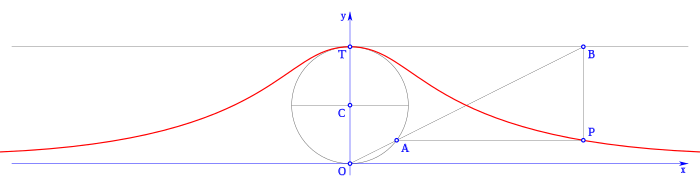
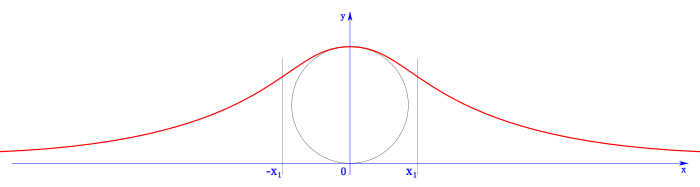
Curva de Agnesi
|
Read other articles:

Politics of Pakistan Federal governmentConstitution of Pakistan Previous constitutions:195619621973 Annex (written 1949, incorporated 1985) Amendments Law Human rights Pakistan Penal CodeLaw enforcement LegislatureParliament of Pakistan National Assembly Leader of the House: Vacant Speaker: Raja Pervaiz Ashraf (PPP) Deputy speaker: Vacant Leader of the Opposition: Vacant Senate Chairman: Sadiq Sanjrani (BAP) Deputy Chairman: Mirza Muhammad Afridi (PTI) Leader of the House: Ishaq Dar (PML(N)) ...

2014 studio album by Houston PersonThe Melody Lingers OnStudio album by Houston PersonReleasedOctober 21, 2014RecordedJune 30, 2014StudioVan Gelder Studio, Englewood Cliffs, NJGenreJazzLength56:55LabelHighNoteHCD 7269ProducerHouston PersonHouston Person chronology Nice 'n' Easy(2013) The Melody Lingers On(2014) Something Personal(2015) The Melody Lingers On is an album by tenor saxophonist Houston Person which was recorded in 2014 and released on the HighNote label.[1] Recepti...

Water utility in Colorado This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Denver Water – news · newspapers · books · scholar · JSTOR (April 2019) (Learn how and when to remove this template message) This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links...

اضغط هنا للاطلاع على كيفية قراءة التصنيف الفصيلة الطُّحَالِيَّة رسم لأحد أنواع سرخس البلوط المرتبة التصنيفية فصيلة[1][2] التصنيف العلمي النطاق: حقيقيات النوى المملكة: النباتات الفرقة العليا: نباتات جنينية القسم: نباتات وعائية الشعبة: حقيقيات الأوراق الشعيبة: سرا

Essehof Gemeinde Lehre Koordinaten: 52° 18′ N, 10° 39′ O52.30638888888910.658333333333Koordinaten: 52° 18′ 23″ N, 10° 39′ 30″ O Einwohner: 395 (1. Sep. 2020)[1] Eingemeindung: 1. Juli 1972 Postleitzahl: 38165 Vorwahl: 05309 DorfgemeinschaftshausDorfgemeinschaftshaus Essehof ist eine Ortschaft in der Gemeinde Lehre im Landkreis Helmstedt in Niedersachsen. Inhaltsverzeichnis 1 Geografie 2 Geschichte 2.1 Ein...

Chiraprapha Maha Devi (Thai: พระนางจิรประภามหาเทวี, RTGS: Phra Nang Chiraprapha Maha Thewi) war zwischen 1545 und 1546 Regentin des Reiches Lan Na in Nord-Thailand[1]. Inhaltsverzeichnis 1 Leben 2 Erwähnenswertes 3 Einzelnachweise 4 Literatur Leben Der Smaragd-Buddha Chiraprapha war eine Tochter von König Ket Chettharat (reg. 1526 bis 1538) und wurde Königin in einer Zeit großer Umbrüche für Lan Na. Sie wurde zur Königin erhoben, währe...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Kelelawar tapal kuda Thai Rhinolophus siamensis Status konservasiRisiko rendahIUCN136651 TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoChiropteraFamiliRhinolophidaeGenusRhinolophusSpesiesRhinolophus siamensis (Gyldenstolpe, 1917) Tata namaPro...

Cerveau humainCerveau et crâne humain.Lobes cérébraux : lobe frontal (rose), lobe pariétal (vert) et lobe occipital (bleu).DétailsSystème Système nerveux centralVascularisation Artère carotides internes, Artères vertébralesDrainage veineux Veines jugulaires internes, veines cérébrales, veines externes, veines choroïdesEmbryologie Tube neuralComprend Télencéphale, tronc cérébral, cerveletIdentifiantsNom latin CerebrumTA98 A14.1.03.001TA2 5415FMA 50801Référence anatomiqu...

Chief Justice of the Hong Kong Court of Final Appeal香港終審法院首席法官IncumbentAndrew Cheungsince 11 January 2021StyleThe Honourable (尊貴的)(formal)NominatorChief ExecutiveAppointerLegislative CouncilTerm lengthTenure until the age of 70[a]Constituting instrumentHong Kong Basic LawInaugural holderAndrew LiFormation1 July 1997; 26 years ago (1997-07-01) Politics and government of Hong Kong Laws Basic Law Drafting Committee Consultative Committee A...

Piala Champions Eropa 1968–69Santiago Bernabéu Stadium in Madrid hosted the final.Informasi turnamenJadwalpenyelenggaraan18 September 1968 – 28 Mei 1969Jumlahtim peserta32Hasil turnamenJuara Milan (gelar ke-2)Tempat kedua AjaxStatistik turnamenJumlahpertandingan52Jumlah gol176 (3,38 per pertandingan)Pencetak golterbanyak Denis Law (9 gol)← 1967–68 1969–70 → Piala Champions Eropa 1968-69 dimenangkan oleh Milan setalah mengalahkan AFC Ajax dengan skor 4-1 di babak fina...

2017 single by Tinashe FlameSingle by Tinashefrom the album Joyride (Japanese edition) ReleasedMarch 16, 2017 (2017-03-16)Recorded2015Genre Alternative R&B synth-pop Length3:06LabelRCASongwriter(s)Tinashe KachingweNolan LambrozaSimon WilcoxIlsey JuberNasri AtwehProducer(s)Sir NolanTinashe singles chronology Quit You (2017) Flame (2017) No Drama (2018) Flame is a song recorded by American singer Tinashe, released on March 16, 2017 as the intended first single from her third ...

German trumpet player 1667–1734 This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (November 2015) (Learn how and when to remove this template message) This article needs ...

1997 single by Mr. President Jojo ActionSingle by Mr. Presidentfrom the album Night Club Released9 June 1997 (1997-06-09)StudioDas Studio, BremenGenreEurodanceLength3:50LabelClub Culture, WEASongwriter(s) Delroy Rennalls Robin Masters Producer(s)Kai MatthiesenMr. President singles chronology Show Me the Way (1996) Jojo Action (1997) Take Me to the Limit (1997) AudioJojo Action on YouTube Jojo Action is a song by German Eurodance group Mr. President, released on 9 June 1997 as t...

American lawyer and politician Senator Duff redirects here. For the Connecticut State Senate member, see Bob Duff. For the Northern Irish senator, see Hugh Duff. James H. DuffUnited States Senatorfrom PennsylvaniaIn officeJanuary 3, 1951 – January 3, 1957Preceded byFrancis J. MyersSucceeded byJoseph S. Clark34th Governor of PennsylvaniaIn officeJanuary 21, 1947 – January 16, 1951LieutenantDaniel B. StricklerPreceded byJohn C. Bell, Jr.Succeeded byJohn S. FineAttorney...

John ElitchJohn and Mary ElitchBornJohn ElitchApril 10, 1852Mobile, AlabamaDiedMarch 10, 1891(1891-03-10) (aged 40)San Francisco, CaliforniaKnown forElitch GardensSpouseMary Elizabeth Hauck (m. 1872) John Elitch Jr. (April 10, 1850 – March 10, 1891) was a restaurateur, businessman, actor, zookeeper, and original owner and namesake of Elitch Gardens and the Elitch Theatre in Denver, Colorado. Early Years and Marriage This section needs additional citations for verification. Please ...

Muhammad Mursiمحمد مرسيPresiden Mesir ke-5Masa jabatan30 Juni 2012 – 3 Juli 2013Perdana MenteriKamal GanzouriHesham QandilWakil PresidenMahmoud MekkiPendahuluMuhammad Hussein Tantawi (Interim)PenggantiAdli Mansur(Interim)Ketua Partai Kebebasan dan KeadilanMasa jabatan30 April 2011 – 24 Juni 2012PemimpinMuhammad BadiePendahuluJabatan ditetapkanPenggantiSaad El-KatatniAnggota Majelis Rakyat MesirMasa jabatan1 Desember 2000 – 12 Desember 2005Pendahulu...

Castello di Monte Sant'AngeloUbicazioneStato attuale Italia RegionePuglia CittàMonte Sant'Angelo IndirizzoLargo Roberto il Guiscardo, 71037 Monte Sant'Angelo Coordinate41°42′27″N 15°57′09.36″E / 41.7075°N 15.9526°E41.7075; 15.9526Coordinate: 41°42′27″N 15°57′09.36″E / 41.7075°N 15.9526°E41.7075; 15.9526 Informazioni generaliTipoCastello normanno - svevo - angioino - aragonese Inizio costruzione837 Condizione attualeRestaurato Propr...

Computer operating system Not to be confused with CICS. Compatible Time-Sharing System (CTSS)Preamble of two versions of the CTSS scheduler, one in MAD and one in FAPDeveloperMIT Computation Center, Project MACWritten inFAP assembly, MADWorking stateDiscontinued, simulator availableSource modelOpen sourceInitial release1961; 62 years ago (1961)Marketing targetColleges and universities[1]Available inEnglishPlatformsIBM 7090, IBM 7094Kernel typeMonolithic, protectedDef...

Santiago metro station SalvadorSantiago Metro stationGeneral informationLocationProvidencia Avenue / Eliodoro Yáñez AvenueCoordinates33°25′57.56″S 70°37′33.91″W / 33.4326556°S 70.6260861°W / -33.4326556; -70.6260861Line(s) Line 1Platforms2 side platformsTracks2ConnectionsTransantiago busesConstructionAccessibleYesHistoryOpenedMarch 31, 1977 [1]Services Preceding station Santiago Metro Following station Baquedanotowards San Pablo Line 1 Manuel Mont...

University in Sri Lanka This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Open University of Sri Lanka – news · newspapers · books · scholar · JSTOR (November 2018) (Learn how and when to remove this template message) The Open University of Sri Lankaශ්රී ලංකා විවෘත විශ්වවිද්යාලය இலங்கை ...