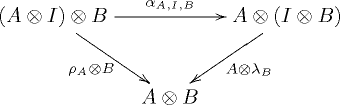
Categoría monoidal
|
Read other articles:

Las referencias de este artículo no tienen un formato correcto. Puedes colaborar editándolas como se indica en esta página.También puedes avisar en su página de discusión a quien las añadió pegando lo siguiente: {{subst:Aviso formato de referencias|Copa de Néstor}} ~~~~Este aviso fue puesto el 28 de julio de 2020. La Copa de Néstor es el nombre que se da en la Ilíada a un recipiente de características especiales que estaba en posesión de Néstor. Néstor era un legendario rey de ...

2016 video gameFIFA 17Cover art featuring Borussia Dortmund's Marco ReusDeveloper(s)EA VancouverEA Romania[1]Publisher(s)EA SportsProducer(s)Aaron McHardyNick ChannonDesigner(s)Matthew PriorComposer(s)Atticus Ross[2]SeriesFIFAEngineFrostbite 3 (PS4, XOne, PC) Ignite (PS3, X360)Platform(s)Microsoft WindowsPlayStation 3PlayStation 4Xbox 360Xbox OneReleaseNA: 27 September 2016WW: 29 September 2016Genre(s)SportsMode(s)Single-player, multiplayer FIFA 17 is a football simulation vid...

Tributary of Saguenay, Quebec (Canada) Ha! Ha! RiverLocationCountryCanadaProvinceQuebecRegionSaguenay–Lac-Saint-JeanRegional County MunicipalityLe Fjord-du-Saguenay Regional County MunicipalityCity and protected areaLaurentides Wildlife Reserve, Ferland-et-Boilleau, Quebec, Saguenay, QuebecPhysical characteristicsSourceMontain and Forest streams • locationLaurentides Wildlife Reserve • coordinates47°51′19″N 70°51′07″W / 47.85528...

Musical by Eddie Perfect, Scott Brown and Anthony King BeetlejuiceThe Musical. The Musical. The Musical.Playbill from the show's original 2019–2020 Broadway run at the Winter Garden TheatreMusicEddie PerfectLyricsEddie PerfectBookScott BrownAnthony KingBasisBeetlejuice by Michael McDowellLarry WilsonWarren SkaarenPremiereOctober 14, 2018: National Theatre, Washington, D.C.Productions2018 Washington, D.C.2019 Broadway 2022 US Tour Beetlejuice is a musical with music and lyrics by Eddie Perfe...

Sweet snack from the Philippines made of corn kernels and shaved ice. Maíz con hieloA maíz con hielo served in glass.CourseSnack, dessertPlace of originPhilippinesServing temperatureColdMain ingredients Shaved ice corn kernels sugar milk Similar dishesSaba con hielo, halo-halo Maíz con hielo (literally corn with ice in Spanish, also commonly spelled mais kon-yelo in Tagalog) is a shaved ice dessert from the Philippines made with boiled corn kernels, sugar, and milk.[1] Ingredients ...

你好,李焕英Hi, Mom基本资料导演贾玲编剧贾玲孙集斌王宇卜钰刘宏禄主演贾玲沈腾陈赫张小斐[1]配乐彭飞大张伟摄影刘寅孙明剪辑叶翔制片商 北京京西文化旅游股份有限公司 上海儒意影视制作有限公司 天津猫眼微影文化传媒有限公司 北京精彩时间文化传媒有限公司 新丽传媒集团有限公司 北京大碗娱乐文化传媒有限公司 浙江横店影业有限公司 阿里巴巴影业(北京)...

Defunct station of the Philippine National Railways (PNR) Northrail line in Pampanga 15°1′36.6″N 120°41′12.15″E / 15.026833°N 120.6867083°E / 15.026833; 120.6867083 San FernandoGeneral informationLocationSan Fernando, PampangaPhilippinesOwned byPhilippine National RailwaysOperated byPhilippine National RailwaysLine(s)Planned: North Commuter Former: North Main LinePlatformsIsland platform (New station)Tracks4 (New station)ConstructionStructure typeAt ...

Kepala BatuAlbum studio karya HelloDirilis16 Agustus 2011GenrePopLabelNagaswaraKronologi Hello Say Hello (2008)String Module Error: Match not foundString Module Error: Match not found Kepala Batu(2011) Kepala Batu adalah album kedua dari grup band Hello yang dirilis pada tahun 2011. Album ini mengusung lagu andalan Pilihan Hati. Daftar lagu Seluruh lagu diciptakan oleh Gavet kecuali yang bertanda Kepala Batu Di Antara Bintang Dua Cincin Pilihan Hati (ft. Mega) Beda Lantai Suka Gila Petual...

High-definition television channel This article is about the former UK channel. For the international channel, see BBC HD (international). For the replacement, see BBC Two. Not to be confused with CBBC HD. Television channel BBC HDLogo used from 2006 to 2013ProgrammingPicture format1080i HDTVOwnershipOwnerBBCSister channelsBBC OneBBC TwoBBC ThreeBBC FourBBC NewsBBC ParliamentCBBCCBeebiesHistoryLaunched15 May 2006; 17 years ago (2006-05-15)Closed26 March 2013; 10...

For other uses, see 27th Brigade. 27th Mountain Infantry Brigade27e Brigade d'Infanterie de MontagneBadge of the 27th Mountain Infantry BrigadeActive1888–presentCountry FranceBranch French ArmyTypeMountain infantrySize~6,500Part of1st DivisionGarrison/HQVarces, FranceCommandersNotablecommandersJean Vallette d'OsiaJacques FaureAlain Le RayMilitary unit The 27th Mountain Infantry Brigade (French: 27e Brigade d'Infanterie de Montagne, 27e BIM) is a mountain infantry formation of the Frenc...

Sanktuarium św. Anny na Górze św. Anny 1/50 z dnia 21 listopada 1950 bazylika mniejsza Widok ogólny Państwo Polska Województwo opolskie Miejscowość Góra Świętej Anny Wyznanie katolickie Kościół rzymskokatolicki bazylika mniejsza od 29 czerwca 1980 Wezwanie św. Anny Historia Data rozpoczęcia budowy XV wiek Data zakończenia budowy 1781, 1957–1963 Dane świątyni Wieża kościelna• liczba wież 1 Organy• liczba głosów• liczba manuałów 263 Położenie na m...

Chinese actor This article is about a Chinese film and stage actor and comedian. For other people, see Chen Qiang. In this Chinese name, the family name is Chen. Chen Qiang陈强Chen Qiang in 1962.BornChen Qingsan (陈庆三)1918Xujiahe Township, Ningjin County, Zhili, ChinaDied26 June 2012(2012-06-26) (aged 93–94)Beijing, ChinaAlma materLu Xun Academy of ArtsOccupation(s)Actor, comedianYears active1950-2001Notable workThe Red Detachment of WomenThe White Haired GirlDevils on...

Nikolaos DendiasΝικόλαος ΔένδιαςMenteri Luar NegeriPetahanaMulai menjabat 9 Juli 2019Perdana MenteriKyriakos MitsotakisPendahuluGeorgios KatrougalosPresiden Komite Menteri Dewan EropaMasa jabatan15 Mei 2020 – 18 November 2020PendahuluDavid ZalkalianiPenggantiHeiko MaasMenteri HukumMasa jabatan8 Januari 2009 – 7 Oktober 2009PendahuluSotirios HatzigakisPenggantiHaris KastanidisMenteri Ketertiban Umum dan Perlindungan Warga NegaraMasa jabatan21 Juni 2012&...

Gaelic inheritance system This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs attention from an expert in United Kingdom. The specific problem is: Lacks content on Manx tanistry, with the article focusing exclusively on Scotland and Ireland. WikiProject United Kingdom may be able to help recruit an expert. (August 2019) This article needs additional citations for verificati...

Ship class of minehunters Sittard Class overview NameDokkum class Builders Arnhemse Scheepsbouw Maatschappij, Arnhem De Noord, Alblasserdam Gusto Shipyard, Schiedam Haarlemse Scheepsbouw Maatschappij, Haarlem J. & K. Smit, Kinderdijk L. Smit en Zoon, Kinderdijk Niestern Scheepsbouw Unie, Hellevoetsluis Wilton-Fijenoord, Schiedam Operators Royal Netherlands Navy Peruvian Navy Succeeded byAlkmaar class SubclassesWildervank Built1953–1957 In commission1955–1999 Planned18...

Crashing the Gate: Netroots, Grassroots, and the Rise of People Powered Politics AuthorJerome Armstrong, Markos MoulitsasCountryUnited StatesLanguageEnglishSubjectAmerican politicsPublisherChelsea GreenPublication dateMarch 1, 2006Media typeHardcoverPages208ISBN1-931498-99-7OCLC62697103Dewey Decimal324.70973 22LC ClassJK1764 .A76 2006Followed byTaking On the System: Rules for Radical Change in a Digital Era Crashing the Gate: Netroots, Grassroots, and the Rise of People P...

Dalzavod Dalzavod (Russian: Центр судоремонта Дальзавод) is a company based in Vladivostok, Russia. Dalzavod was established in 1887 to repair the ships of Russia's Pacific Fleet.[1] The largest defense facility in Vladivostok and one of the largest ship repair yards in Russia, Dalzavod has turned from repair of naval vessels to commercial vessel repair, small boat construction, vehicle repair, and other commercial ventures.[2] As of 2014. Dalzavod emp...

British journalist For the American comedian,, see Kamal Ahmed (comedian). Kamal AhmedAhmed at the 2019 Chiswick Book FestivalBornKamal Ahmed (1967-11-15) 15 November 1967 (age 56)Ealing, London, EnglandEducationDrayton Manor High SchoolAlma materUniversity of LeedsCity University Department of JournalismOccupation(s)Journalist, editor, administratorEmployerBBCTitleEconomics Editor of BBC News (2016–2018)Business Editor of BBC News (2014–2016)Editorial Director of BBC Ne...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (September 2023) Robert SurteesBorn(1779-04-01)1 April 1779South Bailey, DurhamDied14 February 1834(1834-02-14) (aged 54)Mainsforth Hall, County DurhamEducationKepier SchoolHoughton-le-SpringAlma materChrist Church, OxfordNotable worksThe History and Antiquities of the County Palatine of Dur...

For the federal constituency represented in the Dewan Rakyat, see Tawau (federal constituency). Town and district capital in Sabah, MalaysiaTawau TawaoTown and district capitalBandar TawauOther transcription(s) • Jawiتاواو • Chinese斗湖 (Simplified)鬥湖 (Traditional)Dǒuhú (Hanyu Pinyin) • Tamilதவாவ்Tavāv (Transliteration)From top, left to right:City sign, Aerial view towards the town center, Aerial view towards Cowie Bay SealMo...