| Senpintigita 24-ĉelo
|

Figuro de Schlegel kun kubaj ĉeloj montritaj
|

Figuro de Schlegel kun 8 el 24 senpintigitaj okedraj ĉeloj montritaj
|
| Speco
|
Uniforma plurĉelo
|
| Vertica figuro
|
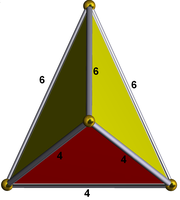
Egallatera triangula piramido (malregula kvaredro)
(3 senpintigitaj okedroj kaj 1 kubo kuniĝas je ĉiu vertico)
|
| Bildo de vertico
|
|
| Simbolo de Schläfli
|
t0,1{3,4,3}
t0,1,2{3,3,4}
t0,1{31,1,1}
|
| Figuro de Coxeter-Dynkin
|
      
      
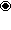    
|
| Verticoj
|
192
|
| Lateroj
|
384
|
| Edroj
|
144 kvadratoj {4}
96 seslateroj {6}
|
| Ĉeloj
|
24 senpintigitaj okedroj (4.6.6) ![]()
24 kuboj (4.4.4) 
|
| Geometria simetria grupo
|
F4 [3,4,3]
B4 [3,3,4]
D4 [31,1,1]
|
| Propraĵoj
|
Konveksa
|
|
En geometrio, la senpintigita 24-ĉelo estas konveksa uniforma plurĉelo. Kiel la nomo sugestas, ĝi povas esti farita per tranĉo de la regula 24-ĉelo je 1/3 de la latera longo.
Ĝi estas barita per 48 ĉeloj: 24 kuboj, kaj 24 senpintigis okedroj.
Strukturo
La 24 kubaj ĉeloj estas kunigitaj tra iliaj kvadrataj edroj al la senpintigitaj okedroj; la 24 senpintigitaj okedroj estas kunigitaj unu al la alia tra iliaj seslateraj edroj.
Projekcioj
La paralela projekcio de la senpintigita 24-ĉelo en 3-dimensian spacon, kun senpintigita okedro unua, estas jena:
- La projekcia koverto estas senpintigita kubokedro.
- 2 el la senpintigitaj okedraj ĉeloj projekciiĝas sur senpintigitan okedron kuŝantan en centro de la koverto.
- 6 kvadrataj prismoj kunigantaj kvadratajn edrojn de ĉi tiu centra senpintigita okedro kun centraj partoj de oklateraj edroj de la senpintigita kubokedro estas la bildoj de 12 el la kubaj ĉeloj, po 2 ĉeloj al ĉiu bildo.
- 12 kvadrataj edroj de la senpintigita kubokedro estas la bildoj de la ceteraj 12 kubaj ĉeloj.
- 6 oklateraj edroj de la senpintigita kubokedro estas la bildoj de 6 el la senpintigitaj okedraj ĉeloj.
- 8 ne-uniformaj senpintigitaj okedroj situantaj inter seslateraj edroj de la projekcia koverto kaj la centra senpintigita okedro estas la bildoj de la ceteraj 16 senpintigitaj okedraj ĉeloj, po 2 ĉeloj al ĉiu bildo.
Bildoj
Vidu ankaŭ